Area del triangolo rettangolo

 - 

Domande e risposte

Come si calcola l’area del triangolo rettangolo? Quali formule si possono utilizzare avendo in alternativa come dati di partenza: i due cateti, un cateto e l’ipotenusa, l’ipotenusa e l’altezza relativa all’ipotenusa, le proiezioni dei cateti sull’ipotenusa oppure un cateto e la sua proiezione sull’ipotenusa? Potreste fornire degli esempi per il calcolo dell’area di un triangolo rettangolo nei vari casi?

Consideriamo un triangolo rettangolo, nel quale indichiamo con {c_1} e {c_2} le misure dei suoi cateti, con {i} la misura dell’ipotenusa e con {h_i} la misura dell’altezza relativa all’ipotenusa.

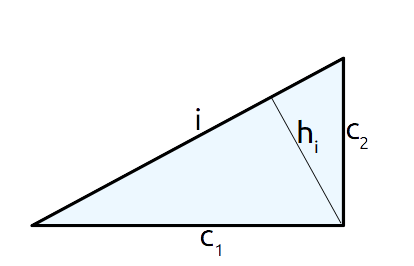
Le formule per calcolare l’area del triangolo rettangolo sono le seguenti:

1) \qquad A = \dfrac{c_1 \cdot c_2 }{2}; \qquad 2) \qquad A = \dfrac{i \cdot h_i}{2}

In particolare, l’area del triangolo rettangolo si può calcolare a partire dai seguenti dati:

• misure dei due cateti;
• misura di un cateto e dell’ipotenusa;
• misure dell’ipotenusa e dell’altezza relativa all’ipotenusa;
• misure delle proiezioni dei cateti sull’ipotenusa;
• misura di un cateto e della sua proiezione sull’ipotenusa.

Nel terzo caso e nel quarto caso utilizzeremo la seconda formula, mentre nei rimanenti casi utilizzeremo la prima.

Ma vediamo subito degli esempi relativi ai vari casi.

Esempio 1

Calcolare l’area di un triangolo rettangolo avente cateti di misura rispettivamente {10 \text{cm}} e {15 \text{cm}}.

Utilizzando la prima formula abbiamo:

A= \dfrac{c_1 \cdot c_2}{2}= \dfrac{10 \text{cm} \cdot 15 \text{cm}}{2}=\dfrac{150}{2} \text{cm}^2 = 75 \text{cm}^2

In pratica abbiamo sostituito nella formula le misure dei cateti del triangolo rettangolo che ci sono state fornite come dati di partenza.

Esempio 2

Calcolare l’area di un rettangolo avente un cateto di misura {20 \text{cm}} e ipotenusa di misura {\text{30} cm}.

Grazie al teorema di Pitagora possiamo ricavare la misura del rimanente cateto. A tal punto sarà possibile calcolare l’area del triangolo utilizzando la prima formula.

\begin{align*} &  c_2 =\sqrt{i^2-c_1 ^2}=\sqrt{(30 \text{cm})^2-(20 \text{cm})^2}=\sqrt{900\text{cm}^2-400 \text{cm}^2}  =  \\ \\ & =\sqrt{500} \text{cm} \approx 22,36 \text{cm} \end{align*}

Ora che disponiamo delle misure di entrambi i cateti possiamo ricavare l’area come detto utilizzando la prima formula:

A= \dfrac{c_1 \cdot c_2}{2}=\dfrac{20 \text{cm} \cdot 22,36 \text{cm}}{2}=223,6 \text{cm}^2

Esempio 3

Calcolare l’area di un triangolo rettangolo avente ipotenusa di misura {45 \text{cm}} e altezza relativa all’ipotenusa di misura {22 \text{cm}}.

L’idea è quella di ricavare l’area del triangolo utilizzando la seconda formula. Infatti, abbiamo come dati di partenza le misure dell’ipotenusa e dell’altezza relativa all’ipotenusa, che sono proprio le grandezze che intervengono nella formula stessa. Abbiamo:

A= \dfrac{i \cdot h_i}{2}=\dfrac{45 \text{cm} \cdot 22 \text{cm}}{2}=\dfrac{990}{2}\text{cm}^2 = 495 \text{cm}^2

Esempio 4

Calcolare l’area di un triangolo rettangolo avente proiezioni sui cateti {p_1} e {p_2} di misura rispettivamente {30 \text{cm}} e {15 \text{cm}}.

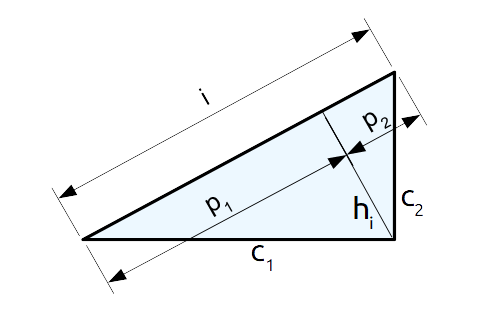
Come possiamo vedere dalla figura, la somma delle due misure delle proiezioni dei cateti sull’ipotenusa è uguale alla misura dell’ipotenusa stessa:

i=p_1 +p_2 = 30 \text{cm} + 15 \text{cm} = 45 \text{cm}

Ora, applicando il secondo teorema di Euclide possiamo ricavare la misura dell’altezza relativa all’ipotenusa:

h_i = \sqrt{p_1 \cdot p_2} = \sqrt{30 \text{cm}\cdot 15 \text{cm}} \approx 21,21 \text{cm}

In pratica abbiamo estratto la radice quadrata del prodotto delle proiezioni dei cateti sull’ipotenusa.

A questo punto avendo ipotenusa e altezza relativa all’ipotenusa possiamo calcolare l’area del triangolo utilizzando la seconda formula:

A = \dfrac{i \cdot h_i}{2}=\dfrac{45 \text{cm} \cdot 21,21 \text{cm}}{2} =477,225 \text{cm}^2

Esempio 5

Calcolare l’area di un triangolo rettangolo avente un cateto di misura {40 \text{cm}} e avente la proiezione di tale cateto sull’ipotenusa di misura {32 \text{cm}}.

Per il primo teorema di Euclide, in un triangolo rettangolo la misura dell’ipotenusa sta alla misura di un cateto come la misura di quello stesso cateto sta alla misura della sua proiezione sull’ipotenusa.

Detta quindi {p_1} la misura della proiezione sull’ipotenusa ad esempio del cateto {c_1} è valida la proporzione:

i:c_1 = c_1 : p_1

In modo del tutto equivalente, osserviamo che ciò significa che in un triangolo rettangolo ciascun cateto è il medio proporzionale tra l’ipotenusa e la proiezione del cateto sull’ipotenusa.

Ora, poiché in una proiezione il prodotto dei medi è uguale al prodotto degli estremi, possiamo scrivere:

i \cdot p_1 = c_1 \cdot c_1

e quindi:

i \cdot p_1 = c_1 ^2

Di conseguenza, ricavando {i}:

i=\dfrac{c_1^2}{p_1}

Poiché come dati di partenza abbiamo proprio {c_1} e {p_1}, utilizzando quest’ultima formula possiamo ricavare la misura dell’ipotenusa:

i=\dfrac{c_1^2}{p_1}=\dfrac{40^2 \text{cm}^2}{32 \text{cm}}=\dfrac{1600}{32} \text{cm} = 50 \text{cm}

Avendo le misure di un cateto e dell’ipotenusa possiamo a questo punto ricavare la misura dell’altro cateto grazie al teorema di Pitagora:

\begin{align*} & c_2 = \sqrt{i^2-c_1^2} = \sqrt{(50 \text{cm})^2-(40 \text{cm})^2}=\sqrt{(2500-1600) \text{cm}^2}= \\ \\ & =\sqrt{900} \text{cm} = 30 \text{cm} \end{align*}

Ma avendo a questo punto le misure di entrambi i cateti possiamo calcolare agevolmente l’area del triangolo utilizzando la prima formula:

A= \dfrac{c_1 \cdot c_2}{2}=\dfrac{40 \text{cm} \cdot 30 \text{cm}}{2}=600 \text{cm}^2

Come ricordare le formule dell’area del triangolo rettangolo

Cerchiamo di giustificare intuitivamente le formule precedentemente viste, in modo da poterle ricordare più facilmente.

In merito alla prima formula:

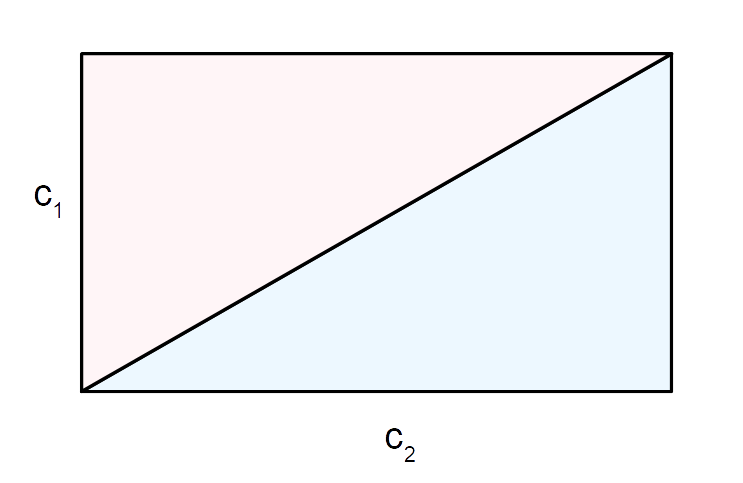
A = \dfrac{c_1 \cdot c_2}{2}

osserviamo che il rettangolo di base {c_1} ed altezza {c_2} è formato da due triangoli rettangoli uguali tra loro aventi entrambi come cateti {c_1} e {c_2}. Così l’area del rettangolo, pari a {c_1 \cdot c_2 }, è il doppio dell’area di ciascun triangolo rettangolo. Di conseguenza, l’area di ciascun triangolo sarà la metà dell’area del rettangolo, ovvero {\dfrac{c_1 \cdot c_2}{2}}.

Quanto alla seconda formula:

A = \dfrac{i \cdot h_i}{2}

questa si giustifica osservando che il rettangolo avente base {i} e altezza {h_i} visibile nella figura seguente ha area doppia rispetto a quella del triangolo rettangolo di ipotenusa {i} e altezza relativa all’ipotenusa {h_i}.

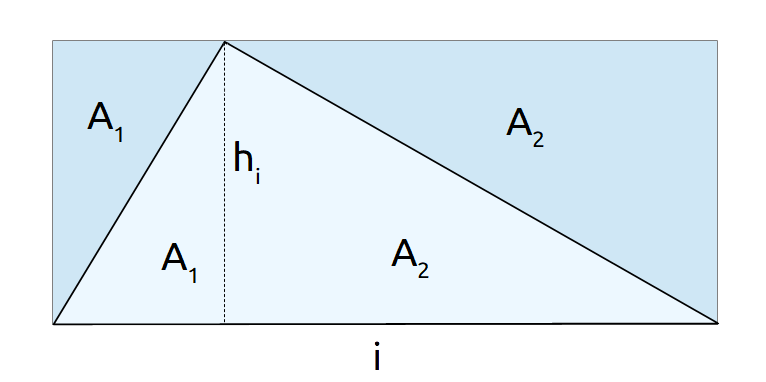
Infatti il triangolo rettangolo di ipotenusa {i} e altezza relativa all’ipotenusa {h_i} è formato da un triangolo rettangolo di area {A_1} e un triangolo rettangolo di area {A_2}. Invece, il rettangolo di base {i} e altezza {h_i} è formato da due triangoli rettangoli di area {A_1} e due triangoli rettangoli di area {A_2}.