Calcolo della circonferenza di un cerchio

 - 

Domande e risposte

Come si effettua il calcolo della circonferenza di un cerchio? Quali sono le formule per calcolare la circonferenza di un cerchio? Come si può calcolare la circonferenza di un cerchio a partire dall’area del cerchio stesso? Potreste fornire degli esercizi ed esempi?

Per calcolare la circonferenza di un cerchio possiamo utilizzare due formule dirette, che utilizzano rispettivamente il raggio e il diametro del cerchio.

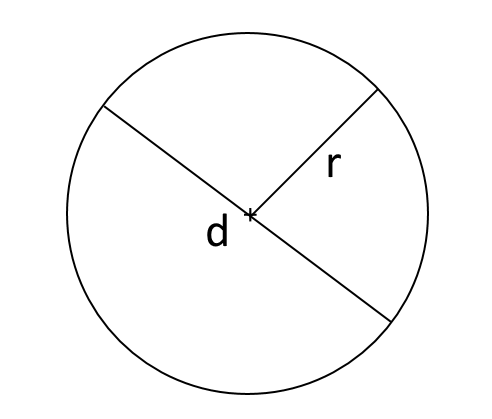
Detti {C} la misura della circonferenza del cerchio, {d} il diametro ed {r} il raggio del cerchio, abbiamo le formule:

C=2 \cdot \pi \cdot  r; \qquad C=\pi \cdot d

Il simbolo {\pi} indica la costante Pi Greco, la quale viene solitamente approssimata con il valore {3,14} (oppure {3,14159} per i calcoli di maggior precisione).

Per il calcolo della circonferenza a partire dall’area {A} del cerchio si può utilizzare la formula:

C=\sqrt{4\cdot \pi \cdot A}

tuttavia può risultare più semplice ricavare prima il raggio, e quindi calcolare la circonferenza:

r=\sqrt{\dfrac{A}{\pi}} , \qquad C=2 \cdot \pi \cdot r

Infatti è forse più facile ricordare la formula del raggio a partire dall’area rispetto alla formula della circonferenza a partire dall’area.

Vediamo subito degli esempi sul calcolo della circonferenza di un cerchio, nei vari casi.

Esempio 1

Calcolare la circonferenza di un cerchio avente raggio {5 \text{cm}}.

Utilizzando la formula {C=2 \cdot \pi \cdot r} abbiamo:

C=2 \cdot \pi \cdot r=2 \cdot 3,14 \cdot 5 \text{cm} \approx 31,4 \text{cm}

In pratica per calcolare l’area del cerchio a partire dal suo raggio basta moltiplicare il raggio per due e per Pi Greco.

Esempio 2

Calcolare la circonferenza di un cerchio avente diametro {7 \text{cm}}.

Utilizzando la formula {C=\pi \cdot d} abbiamo:

C=\pi \cdot d=3,14 \cdot 7 \text{cm} = 21,98 \text{cm}

In pratica per calcolare la circonferenza di un cerchio a partire dal diametro, basta moltiplicare il diametro per la costante Pi Greco.

Esempio 3 (calcolo della circonferenza di un cerchio a partire dall’area)

Vediamo ora come calcolare la circonferenza di un cerchio avendo come dato di partenza l’area del cerchio stesso.

Calcolare la circonferenza di un cerchio avente area {200 \text{m}^2}.

Possiamo utilizzare due metodi. Nel primo metodo, ricaveremo il raggio dall’area e quindi la circonferenza dal raggio. Nel secondo metodo, ricaveremo direttamente la circonferenza dall’area del cerchio.

Primo metodo. Cominciamo ricavando il raggio del cerchio a partire dall’area:

r=\sqrt{\dfrac{A}{\pi}}=\sqrt{\dfrac{200 \text{m}^2}{3,14}} \approx 7,98 \text{m}

Concludiamo calcolando la circonferenza:

C=2 \cdot \pi \cdot r = 2 \cdot 3,14 \cdot 7,98 \approx 50,11 \text{m}

Secondo metodo. Calcoliamo direttamente la circonferenza del cerchio a partire dall’area:

\begin{align*} & C=\sqrt{4 \cdot \pi \cdot A}=\sqrt{4 \cdot 3,14 \cdot 200 \text{m}^2}=\\ \\ & =\sqrt{2512 \text{m}^2} \approx 50, 12 \text{m} \end{align*}

Approssimazioni a parte i due metodi per il calcolo della circonferenza del cerchio a partire dall’area portano allo stesso risultato.

Per quanto riguarda il calcolo della circonferenza del cerchio con esercizi di esempio è tutto. Buon proseguimento!