Il coefficiente angolare m di una retta nel piano è il rapporto tra la differenza delle ordinate e la differenza delle ascisse di due qualsiasi punti distinti della retta stessa. In ciascuna differenza abbiamo come minuendo la coordinata relativa al secondo punto lungo un dato asse e come sottraendo la coordinata relativa al primo punto lungo quello stesso asse.
Così, dati due punti P1 = (x1, y1) e P2 = (x2, y2) appartenenti ad una retta, il coefficiente angolare della retta stessa è dato da m = (y2 – y1) / (x2 – x1).
Per ricavare la definizione di coefficiente angolare mostreremo un semplice metodo che si basa sul primo principio di equivalenza delle equazioni, e consiste nell’applicare la condizione di appartenenza ad una retta relativamente a due punti della retta stessa, dei quali sono note le coordinate cartesiane.
Nel corso della lezione mostreremo inoltre la differenza che intercorre tra i due casi nei quali il coefficiente angolare della retta considerata sia rispettivamente positivo o negativo. In ciascun caso, come vedremo, sarà possibile trarre opportune conclusioni circa la crescenza o decrescenza della funzione lineare corrispondente alla retta in esame, ed anche relativamente all’angolo {\alpha} che la retta stessa forma con la direzione positiva dell’asse delle {x}.
Definizione di coefficiente angolare
Consideriamo una retta {r} del piano cartesiano di equazione (esplicita):
y=mx+q
A tale retta corrisponde la funzione lineare:
f(x)=mx+q
ove si è semplicemente posto {y=f(x)}, il che equivale ad esprimere la variabile dipendente {y} in funzione della variabile indipendente {x}.
Il coefficiente del termine in {x} al secondo membro delle precedenti uguaglianze, ovvero {m}, si chiama coefficiente angolare della retta {r}. E come dimostreremo tra breve, per il coefficiente angolare di una data retta {r} vale la seguente definizione.
Dati due punti {P_1 = (x_1, y_1)} e {P_2 = (x_2, y_2)}, con {x_1 \neq x_2}, il coefficiente angolare della retta {r} passante per i due punti stessi è dato da: {m=\dfrac{y_2-y_1}{x_2-x_1}}ovvero dal rapporto tra la differenza delle coordinate lungo l’asse {y} del secondo punto e del primo punto e la differenza delle coordinate lungo l’asse {x} sempre del secondo punto e del primo punto.
E’ importante osservare che sia a numeratore, sia a denominatore le coordinate si presentano nello stesso ordine. Infatti, sia a numeratore, sia a denominatore il minuendo è la coordinata relativa al punto {P_2} mentre il sottraendo è la coordinata relativa al punto {P_1}. Ricordiamo che in una differenza il minuendo è il primo numero, mentre il sottraendo è il secondo numero. Così, in generale, nella differenza {a-b} il minuendo è {a} mentre il sottraendo è {b}.
Ora, per note proprietà elementari dell’algebra è evidente che il coefficiente angolare può anche essere espresso in modo del tutto equivalente come:
m=\dfrac{y_1-y_2}{x_1-x_2}infatti:
\dfrac{y_1-y_2}{x_1-x_2}=\dfrac{-(-y_1+y_2)}{-(-x_1+x_2)}=\dfrac{-(y_2-y_1)}{-(x_2-x_1)}=\dfrac{y_2-y_1}{x_2-x_1}L’ultimo passaggio si giustifica banalmente osservando che “meno diviso meno dà più”.
Ora, è altrettanto importante osservare che entrambe le seguenti espressioni per il coefficiente angolare {m} sono invece sbagliate:
\cancel{m=\dfrac{y_2-y_1}{x_1-x_2}}; \qquad \cancel{m=\dfrac{y_1-y_2}{x_2-x_1}} \qquad \text{NO!}Infatti, le differenze a numeratore e denominatore non contengono le coordinate dei due punti nello stesso ordine.
Infine, per meglio ricordare la definizione di coefficiente angolare, possiamo esprimerla nella forma sintetica:
m=\dfrac{\Delta y}{\Delta x}con {\Delta y = y_2-y_1} e {\Delta x = x_2- x_1}, ove {\Delta y} e {\Delta x} sono gli incrementi di ciascuna coordinata lungo l’asse {y} e l’asse {x} corrispondenti ai due punti {P_1=(x_1, y_1)} e {P_2 = (x_2, y_2)}, appartenenti ad una data retta {r}. Il rapporto {\dfrac{\Delta y}{\Delta x}} si dice rapporto incrementale della funzione {f(x)=mx + q} corrispondente alla retta {r}.
Vediamo ora come ricavare in modo ragionato la definizione appena data di coefficiente angolare.
Definizione di coefficiente angolare di una retta mediante il primo principio di equivalenza
Come abbiamo visto nella precedente lezione sull’equazione esplicita di una retta del piano, se un certo punto {P_1 = (x_1, y_1)} appartiene ad una retta {r} di equazione {y=mx+q}, allora necessariamente vale l’uguaglianza:
y_1=mx_1+q \qquad (1)
D’altro canto, se anche il punto {P_2 = (x_2, y_2)} appartiene alla retta {r}, deve allora necessariamente valere pure la seguente uguaglianza:
y_2 = mx_2 + q \qquad (2)
Tali uguaglianze rappresentano le condizioni di appartenenza alla retta {r} dei punti {P_1} e {P_2}.
Ora, per il primo principio di equivalenza delle equazioni, sarà anche valida la nuova equazione che si ottiene sottraendo membro a membro la seconda equazione alla prima:
y_2-y_1 = m x_2+q-(m x_1+q),\qquad (2)-(1)
Infatti, grazie al primo principio di equivalenza, detta {Q} una quantità tale da rispettare opportune ipotesi, possiamo riscrivere la seconda equazione come:
y_2 - Q = mx_2 + q - Q
Ma per la (1) possiamo indifferentemente porre {Q=y_1} oppure {Q=mx_1 + q}. Di conseguenza, sostituendo nel primo membro a {Q} la quantità {y_1} e nel secondo membro a {Q} la quantità {mx_1+ q} ritroviamo effettivamente:
y_2-y_1=mx_2+q-(mx_1+q)
Ora, sviluppando i calcoli al secondo membro:
y_2-y_1 =mx_2+\cancel{q}-mx_1-\cancel{q} \quad \Rightarrow \quad y_2-y_1=m(x_2-x_1)da cui in conclusione ricavando {m}:
m=\dfrac{y_2-y_1}{x_2-x_1}Ritroviamo così la definizione precedentemente data di coefficiente angolare della retta {r} passante per i due punti {P_1} e {P_2}.
Osserviamo che la definizione data di coefficiente angolare è valida presi due qualsiasi punti appartenenti alla retta {r}. Ciò è evidente poiché le coordinate di un qualunque punto appartenente alla retta rispettano la relazione {y=mx + q}.
Tuttavia, ciò si giustifica anche utilizzando i criteri di similitudine dei triangoli. Consideriamo infatti la seguente figura:
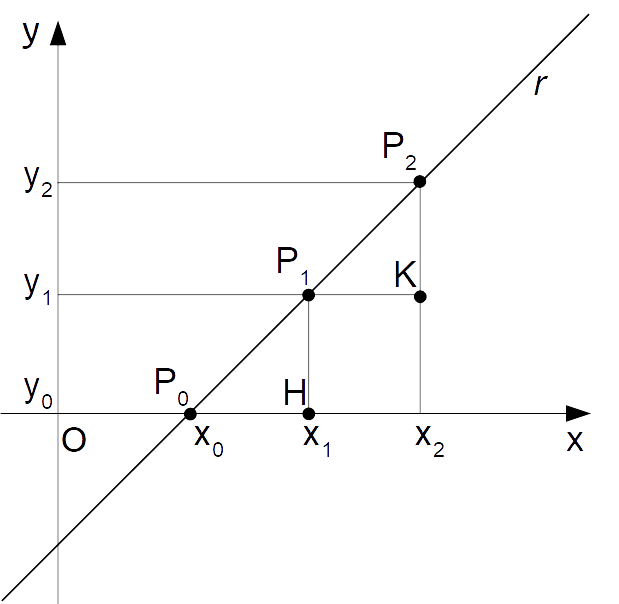
Dati tre punti {P_0, \: P_1} e {P_2} appartenenti ad una data retta {r}, è possibile individuare i due triangoli rettangoli {\stackrel{\triangle}{P_0P_1H}} e {\stackrel{\triangle}{P_1P_2K}}.
Poiché i due triangoli sono simili, è possibile scrivere la seguente proporzione ove compaiono le misure dei rispettivi cateti:
\overline{P_1H}:\overline{P_0H} = \overline{P_2K} : \overline{P_1K}ovvero, esprimendo ciascuna lunghezza utilizzando le coordinate cartesiane:
|y_1-y_0|:|x_1-x_0| = |y_2-y_1| : |x_2-x_1|
Ora, la proporzione rimane valida anche utilizzando le lunghezze algebriche dei lati dei triangoli, ovvero togliendo i simboli di valore assoluto:
(y_1-y_0) :(x_1-x_0) = (y_2-y_1):(x_2-x_1)
Infine, utilizzando i simboli di fratto:
\dfrac{y_1-y_0}{x_1-x_0}=\dfrac{y_2-y_1}{x_2-x_1}Ora, osserviamo che al primo membro abbiamo il coefficiente angolare della retta espresso mediante le coordinate dei punti {P_0} e {P_1}, mentre al secondo membro abbiamo lo stesso coefficiente angolare ma espresso mediante le coordinate dei punti {P_1} e {P_2}. Così in conclusione, sussistendo tale uguaglianza ritroviamo che il coefficiente angolare di una retta {r} può essere definito e quindi calcolato a partire da due qualsiasi punti appartenenti alla retta stessa.
Crescenza e decrescenza di una funzione lineare e segno del coefficiente angolare della retta corrispondente
Importante. In questa parte della lezione presentiamo delle considerazioni che si basano sui concetti di funzioni crescenti e decrescenti. Tuttavia, tali nozioni solitamente non fanno parte degli argomenti che sono a conoscenza degli studenti che si apprestano per la prima volta allo studio della retta. Di conseguenza, chi non conosce ancora le nozioni di crescenza e decrescenza delle funzioni può passare direttamente alle conclusioni a seguire.
In generale una funzione {f(x)} risulta (strettamente) crescente nel suo dominio se per ogni coppia di punti {x_1, x_2} del dominio stesso, con {x_2 > x_1} risulta:
f(x_2) > f(x_1)
Viceversa, una funzione {f(x)} risulta (strettamente) decrescente nel suo dominio se per ogni coppia di punti {x_1, x_2} del dominio stesso, con {x_2 > x_1} risulta:
f(x_2) < f(x_1)
Ora, nel caso di una funzione lineare del tipo:
f(x)=mx+q, \qquad m, q \in \R
è opportuno stabilire quali conclusioni si possono trarre a proposito della crescenza e della decrescenza della funzione nel suo dominio, nei due distinti casi di coefficiente angolare {m} positivo oppure negativo. In tal modo, poiché detta funzione lineare ha per grafico come sappiamo una retta, sarà possibile stabilire una caratterizzazione per le rette aventi rispettivamente coefficiente angolare positivo e negativo.
In particolare, se il coefficiente angolare {m} è positivo, al crescere di {x} crescerà anche la quantità {mx}. Così, se {x_2 > x_1}, la differenza:
f(x_2)-f(x_1)
ovvero:
mx_2+\cancel{q}-mx_1-\cancel{q}, \quad \Rightarrow \quad mx_2-mx_1risulterà positiva, in quanto {mx_2 > mx_1} poiché {m > 0}. Possiamo quindi scrivere:
mx_2 -mx_1 > 0 \iff mx_2 > mx_1 \iff f(x_2)> f(x_1) \quad \text{con} \quad x_2 > x_1Di conseguenza se {m> 0 } la funzione lineare {y=mx+q} risulta strettamente crescente nel suo dominio.
In modo del tutto simile si può mostrare che la funzione {y=mx+q} nel caso in cui sia {m < 0 } risulta strettamente decrescente nel suo dominio. Infatti, se {m<0} al crescere della {x} la quantità {mx} risulterà decrescente. Infatti, una quantità negativa diviene sempre più piccola al crescere del suo valore assoluto. Così, in breve, se {m< 0} e se {x_2 > x_1} possiamo scrivere:
mx_2 < mx_1 \iff f(x_2) < f(x_1) \qquad \text{con} \quad x_2 > x_1da cui risulta che se {m < 0} la funzione {y=mx+q} risulta (strettamente) decrescente.
Nota. Osserviamo che l’avverbio “strettamente” si riferisce al fatto che le funzioni che stiamo considerando soddisfano soltanto disuguaglianze tra le loro valutazioni in due distinti punti. In altre parole, dati due distinti punti {x_1} e {x_2} nel dominio di una funzione lineare del tipo {y=mx+q} con {m \neq 0}, sarà sempre non verificata l’uguaglianza {f(x_1)=f(x_2)}.
Infine, precisiamo che il dominio di una funzione lineare del tipo {y=mx+q} è dato dall’intero insieme dei numeri reali. Non esiste infatti alcun valore reale della {x} tale da far perdere significato all’espressione {mx+q}, con {m, q \in \R}.
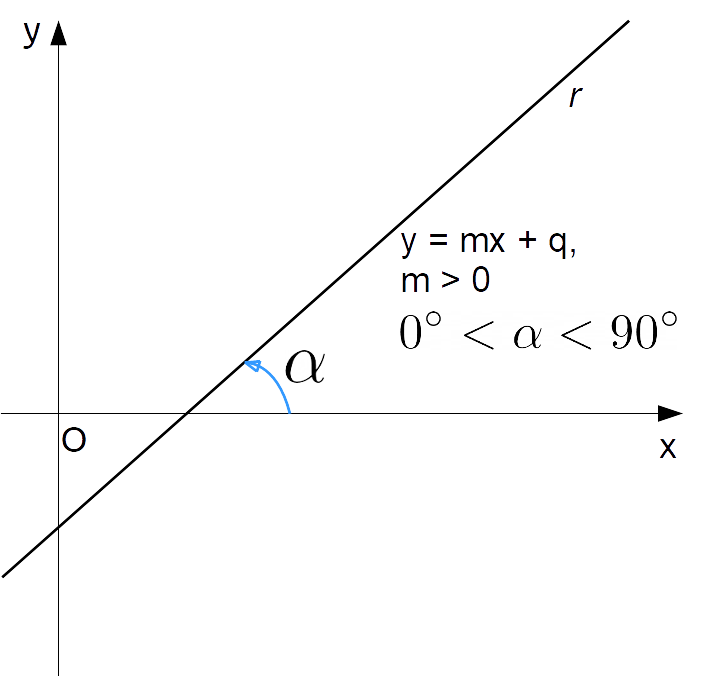
Tutto quanto sinora detto ha per conseguenza che se {m>0} la funzione lineare {y=mx+q} ha il seguente andamento:
mentre se {m<0} la funzione lineare {y=mx+q} ha invece il seguente andamento:
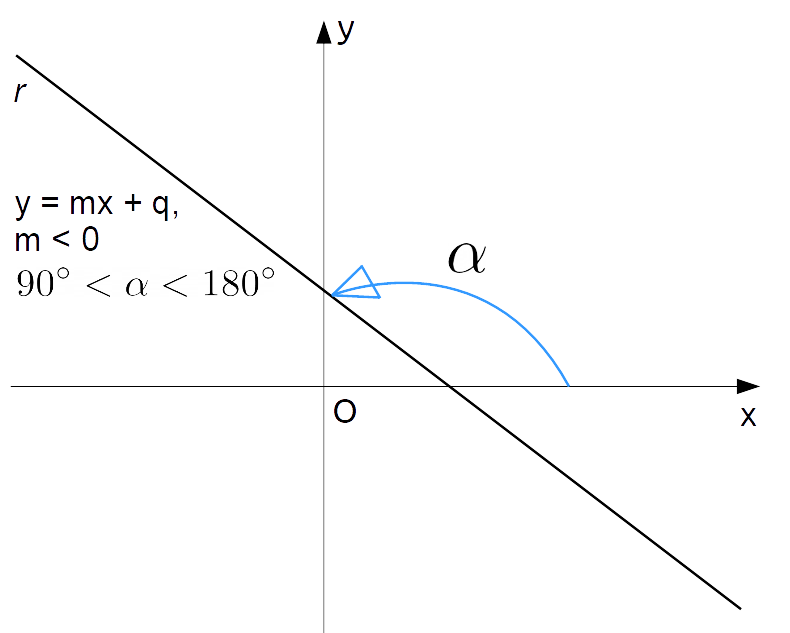
Come è immediato verificare, nel primo caso l’angolo {\alpha} che la retta di equazione {y=mx+q} forma con la direzione positiva dell’asse delle {x} è compreso tra 0 e 90 gradi (valori estremi esclusi). Viceversa, nel secondo caso tale angolo è compreso tra 90 e 180 gradi (valori estremi esclusi).
Infine, se {m=0} l’equazione della retta {r} si riduce a {y=q} e quindi otteniamo una retta parallela all’asse delle {x}, con {\alpha = 0}. In tal caso la funzione lineare corrispondente alla retta in esame non è né strettamente crescente né strettamente decrescente, ed infatti risulta costante, ovvero tale da rispettare l’uguaglianza:
f(x_1)=f(x_2)
presi due punti qualsiasi del suo dominio.
Quindi, riepilogando possiamo affermare quanto segue.
Data una retta {r} di equazione esplicita {y=mx+q}, ed indicato con {\alpha} l’angolo che la stessa retta {r} forma con la direzione positiva dell’asse {x}, si hanno i seguenti distinti casi in base al segno del coefficiente angolare {m}: {\begin{align*} & m > 0 \quad \Rightarrow \quad 0^{\circ} <\alpha < 90^{\circ} \\ \\ & m< 0 \quad \Rightarrow \quad 90^{\circ} < \alpha < 180^{\circ} \\ \\ & m = 0 \quad \Rightarrow \quad \alpha = 0^{\circ} \end{align*}}Nel primo caso la funzione lineare {y=mx+q} risulta strettamente crescente, nel secondo caso risulta strettamente decrescente ed infine nel terzo caso risulta costante (infatti per {m=0} l’equazione della retta si riduce a {y=q}, ovvero l’equazione di una retta parallela all’asse delle {x}).
Importante. Ricordiamo che l’angolo {\alpha} è inteso come un angolo positivo (descritto per definizione in senso antiorario), avente come primo lato la direzione positiva dell’asse delle {x} e come secondo lato la retta {r}. Per ulteriori dettagli, vedi la lezione sulla retta passante per l’origine.
Coefficiente angolare a partire dall’equazione di una retta in forma implicita
Come già anticipato in questa lezione sull’equazione di una retta nel piano, l’equazione di una retta del piano in forma implicita è data da:
ax+by+c=0, \qquad a,b,c \in \R
Nell’ipotesi in cui sia {b \neq 0}, dividendo entrambi i membri dell’equazione per {b} otteniamo:
\dfrac{a}{b}x+y+\dfrac{c}{b}=0da cui ricavando la {y}:
y=-\dfrac{a}{b}x-\dfrac{c}{b}Ma a questo punto confrontando l’equazione appena scritta con l’equazione di una retta del piano in forma esplicita:
y=mx+q
ricaviamo:
m=-\dfrac{a}{b}, \qquad q=-\dfrac{c}{b}per cui in conclusione il coefficiente angolare di una retta di equazione in forma implicita {ax+by+c=0} è dato da {m=-\dfrac{a}{b}}.
Nota. Nel caso in cui sia {b=0} l’equazione di una retta si riduce alla forma {x=k, \: k \in \R}. In tal caso abbiamo una retta verticale (ovvero parallela all’asse {y}), per la quale il coefficiente angolare non è definito. Infatti, in una retta verticale le ascisse di tutti i suoi punti hanno lo stesso valore, e di conseguenza riprendendo la definizione di coefficiente angolare, ovvero: {m=\dfrac{y_2-y_1}{x_2-x_1}} con {P_1=(x_1, y_1)} e {P_2=(x_2, y_2)} punti appartenenti alla retta, è immediato osservare che il denominatore {x_2-x_1} è nullo (le due ascisse sono uguali). Di conseguenza, la frazione algebrica corrispondente al coefficiente angolare non ha significato e quest’ultimo pertanto non è definito.
Legame tra coefficiente angolare ed angolo che la retta forma con la direzione positiva dell’asse x
Abbiamo visto come esiste un legame tra il coefficiente angolare {m} di una retta {r} del piano e l’angolo {\alpha} che tale retta forma con la direzione positiva dell’asse {x}.
Vogliamo ora mostrare come sia possibile effettivamente ricavare un’uguaglianza che stabilisce formalmente la relazione che intercorre tra il coefficiente angolare {m} e l’angolo {\alpha}.
Consideriamo due punti appartenenti ad una data retta {r}. Grazie ad essi è possibile individuare un triangolo rettangolo come in figura.
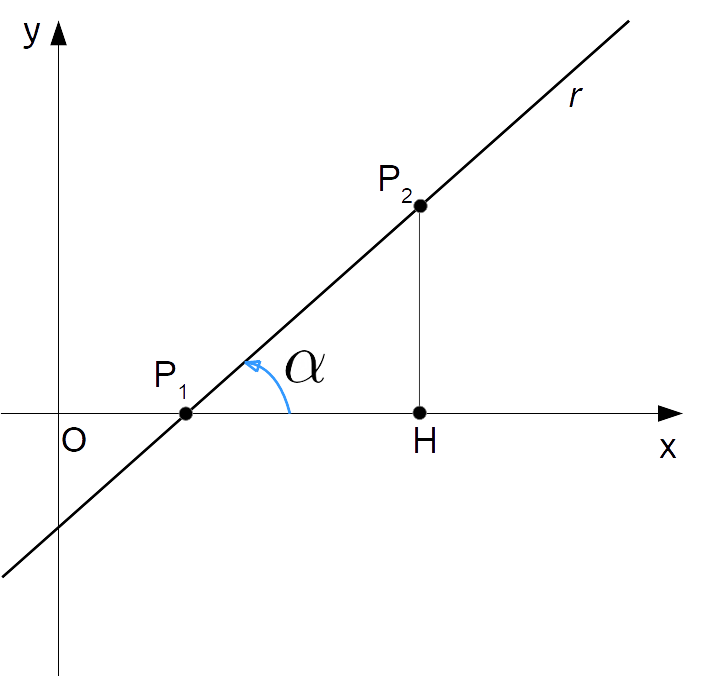
In particolare, considerato il triangolo rettangolo {\stackrel{\triangle}{P_1P_2H}}, la tangente dell’angolo {\alpha} è data per definizione dal rapporto tra la misura del cateto opposto all’angolo {\alpha} e la misura del cateto adiacente all’angolo stesso:
\tan \alpha = \dfrac{\overline{P_2H}}{\overline{P_1H}}Ora, se indichiamo le coordinate dei vertici del triangolo come:
P_1=(x_1, y_1), \quad P_2=(x_2, y_2), \quad H=(x_2, y_1)
allora la precedente diviene:
\tan \alpha = \dfrac{|y_1 - y_2|}{|x_2-x_1|}=\dfrac{y_2-y_1}{x_2- x_1}=mda cui segue:
m = \tan \alpha
Il coefficiente angolare {m} di una data retta {r} è dunque uguale alla tangente dell’angolo {\alpha} che la retta stessa forma con la direzione positiva dell’asse delle {x}.
Di conseguenza, tenendo conto delle opportune ipotesi sull’invertibilità della funzione tangente, si ha:
\alpha = \arctan (m)
ove con il simbolo {\arctan} indichiamo la funzione arcotangente, che sotto le opportune ipotesi è la funzione inversa della funzione tangente.
E’ dunque possibile ricavare, a partire dal coefficiente angolare di una retta, l’angolo {\alpha} che questa forma con la direzione positiva dell’asse delle {x}.
Per ulteriori informazioni sulle funzioni tangente ed arcotangente, ed in generale sulle funzioni trigonometriche, rimandiamo a successive lezioni.
Esempi
A conclusione della lezione vediamo alcuni esempi sul calcolo del coefficiente angolare di una retta del piano.
Esempio 1
Calcolare il coefficiente angolare della retta del piano passante per i punti {P_1=(5,6)} e {P_2=(1,2)}.
Abbiamo {P_1=(x_1, y_1)=(5,6)} e {P_2 = (x_2, y_2) = (1,2)}, da cui {x_1=5, x_2 = 1, y_1 = 6} e {y_2 = 2}. Di conseguenza, utilizzando la definizione di coefficiente angolare in funzione delle coordinate cartesiane di due punti appartenenti alla retta in esame si ha:
m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{2-6}{1-5}=\dfrac{-4}{-4}=1Per cui la retta considerata ha coefficiente angolare {m=1}. E di conseguenza, la retta forma con la direzione positiva dell’asse delle {x} un angolo {\alpha} uguale a:
\alpha = \arctan (1) = 45^{\circ}(la funzione arcotangente è disponibile in qualsiasi calcolatrice scientifica).
Esempio 2
Calcolare il coefficiente angolare della retta di equazione {y=2x+7}.
In realtà non è necessario alcun calcolo, ma è sufficiente confrontare l’equazione data con la forma generale dell’equazione di una retta del piano in forma esplicita:
y=mx+q
da cui si deduce immediatamente che nel nostro caso abbiamo {m=2}. Di conseguenza, il coefficiente angolare della retta data è uguale a {2}.
Esempio 3
Calcolare il coefficiente angolare della retta del piano avente equazione {2x-5y+8=0}.
In questo caso l’equazione della retta si presenta in forma implicita e non è di conseguenza possibile ricavare immediatamente il coefficiente angolare. Tuttavia, basta ricordare che si ha in generale:
m= -\dfrac{a}{b}La relazione in questo caso è valida poiché effettivamente abbiamo {b \neq 0}. In particolare, dal confronto dell’equazione data con quella in forma generale {ax+by+c=0} deduciamo immediatamente che nel nostro caso si ha {a = 2} e {b=-5}. Di conseguenza possiamo calcolare il coefficiente angolare della retta assegnata come:
m = -\dfrac{a}{b}=-\dfrac{2}{-5}=\dfrac{2}{5}Come sempre prestiamo attenzione ai segni nei calcoli.
Conclusioni
Per questa lezione sul coefficiente angolare di una retta nel piano cartesiano è tutto. Abbiamo così visto la definizione di coefficiente angolare e come ricavarlo a partire dall’equazione di una retta data sia informa esplicita, sia in forma implicita. Nella prossima lezione vedremo più nel dettaglio l’equazione di una retta in forma implicita. Buon proseguimento con SìMatematica! 🙂
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
