Definizione di valore assoluto (introduzione alle equazioni con modulo)

 - 

Equazioni (superiori)

In questa lezione esaminiamo la definizione di valore assoluto (o modulo), relativamente alle due versioni utilizzate rispettivamente alle scuole medie e alle superiori (ed università).

Il concetto di valore assoluto è fondamentale per poter risolvere tutta una serie di esercizi relativi alle equazioni, alle disequazioni e al calcolo differenziale. La prima volta che si incontra la definizione di valore assoluto è alle medie, nell’ambito del calcolo con i numeri relativi. Successivamente, lo ritroviamo alle superiori a partire dai radicali, per poi passare alle equazioni e disequazioni con modulo, fino al calcolo differenziale (limiti, derivate, integrali e studio di funzione).

E’ dunque importante aver ben presente la definizione di valore assoluto (o modulo). E in questa lezione ci proporremo anche di chiarire la differenza tra la definizione così come viene presentata alle medie e la definizione utilizzata alle superiori e all’università.

Infine, nella seconda parte della lezione forniremo un’introduzione alle equazioni con valori assoluti, che poi tratteremo in modo più approfondito nella lezione successiva.

Prima di iniziare, precisiamo che il valore assoluto di una quantità si indica ponendo la quantità stessa all’interno dei simboli {||}. Così ad esempio il valore assoluto di {5} si indicherà con {|5|}.

Prima definizione di valore assoluto (scuole medie)

Il valore assoluto di un numero intero relativo è il corrispondente numero naturale che ha le sue stesse cifre.

Così ad esempio dato il numero intero relativo {+45}, secondo tale definizione il corrispondente valore assoluto è il numero naturale {45}. Dato inoltre il numero intero relativo {-33}, il suo valore assoluto è il numero naturale {33}.

In modo informale possiamo dire che secondo questa definizione il valore assoluto di un numero relativo è dato da quel numero privato del segno. La definizione non è del tutto corretta ma comunque accettabile.

La funzione valore assoluto stabilisce quindi una corrispondenza tra l’insieme dei numeri interi relativi e l’insieme dei numeri naturali. Così, ai numeri interi relativi -17 e +17 corrisponderà il numero naturale 17, ai numeri -46 e +46 corrisponderà il numero naturale 46, e così via.

La definizione così posta riesce utile nel calcolo con i numeri relativi. Ad esempio, dovendo eseguire la somma algebrica:

+17-49

basterà sottrarre tra loro i valori assoluti dei numeri dati, e quindi attribuire al risultato il segno del numero più grande in valore assoluto fra i numeri di partenza. Così:

• il valore assoluto di {+17} è il numero naturale {17};
• il valore assoluto di {-49} è il numero naturale {49};
• la differenza tra i valori assoluti è il numero naturale {49-17=32};
• il risultato avrà il segno di {-49}, che il numero con il valore assoluto più grande fra i numeri di partenza. Così in conclusione abbiamo {+17-49=-32}.

Osserviamo che la sottrazione {49-17} ha senso nell’insieme dei numeri naturali, ma sempre in tale insieme la sottrazione {17-49} è priva di significato. Riesce allora comodo lavorare con i numeri naturali in modo da non avere equivoci sul come eseguire la sottrazione tra i valori assoluti. Di qui la definizione di valore assoluto che stabilisce una corrispondenza tra numeri interi relativi e numeri naturali.

Definizione di valore assoluto per superiori ed università

Nei casi più generali la definizione di valore assoluto precedentemente fornita risulta inadeguata. Spesso si ha infatti bisogno di considerare il valore assoluto di una quantità pur rimanendo nell’insieme dei numeri reali. In molte situazioni non conviene definire il valore assoluto di un numero reale come un numero naturale.

Interviene allora la seguente definizione, che è quella in uso alle scuole superiori e nelle facoltà universitarie.

Il valore assoluto (o modulo) di una quantità reale {x} è dato da {+x} se il numero di partenza è positivo, {0} se il numero di partenza è nullo, {-x} se il numero di partenza è negativo.

In altri termini, secondo questa definizione il valore assoluto di un numero è quello stesso numero forzato positivo. Così ad esempio il valore assoluto di {-2} è {+2}, il valore assoluto di {+45} è {+45} e il valore assoluto di {-\sqrt{2}} è {+\sqrt{2}}.

Per quanto riguarda una quantità generica nell’incognita {x}, ad esempio {x-2}, il suo valore assoluto è:

• {x-2} se {x-2 \geq 0};
• {-(x-2)=-x+2=2-x} se {x-2 < 0}.

Come è immediato osservare, nel caso di una quantità incognita basta applicare la stessa definizione per le quantità numeriche, ricordando la definizione di polinomio opposto.

Come vedremo fra un istante, un’importante applicazione della definizione di valore assoluto (nella seconda variante appena data) è costituita dalle equazioni con valore assoluto. In questa lezione vedremo una semplice introduzione alle equazioni con valore assoluto, rimandandone uno studio più approfondito ad una successiva lezione.

Introduzione alle equazioni con valore assoluto

Le equazioni con valore assoluto (o equazioni con modulo) sono particolari equazioni nelle quali l’incognita compare all’interno del simbolo di modulo. Una semplice equazione con valore assoluto è ad esempio la seguente:

|P(x)|=k, \qquad k  \in \mathbb{R}

ove {P(x)} è un polinomio e {k} è una costante reale.

Osserviamo che poiché il valore assoluto è una quantità sempre positiva, se {k<0} l’equazione {P(x)=k} è impossibile. Infatti, abbiamo il primo membro positivo e il secondo membro negativo.

Nel caso in cui sia {k=0} l’equazione si riduce a {P(x)=0}.

Infine, qualora sia {k>0} l’equazione avrà per soluzioni l’unione degli insiemi delle soluzioni delle equazioni {P(x)=k} e {P(x)=-k}. Ciò discende direttamente dalla definizione di valore assoluto. Infatti se {|P(x)|=k} allora {P(x)} potrà essere uguale a {k} oppure a {-k}. Infatti il valore assoluto di {k} o di {-k} è proprio {k}.

Ora, consideriamo ad esempio l’equazione:

|2-x|=5

Abbiamo un’equazione con valore assoluto del tipo indicato con {P(x)=2-x} e {k=5}. Per risolvere l’equazione dobbiamo trovare il valore o i valori della {x} per il quale risulti che il valore assoluto della quantità {2-x} è uguale a {5}.

Si tratterà quindi di risolvere le equazioni:

2-x = 5; \qquad -(2-x)=5

ed unire le corrispondente soluzioni. Per la prima equazione abbiamo:

2-x=5 \quad \Rightarrow \quad -x=5-2 \quad \Rightarrow \quad x=-3

mentre per la seconda equazione:

-(2-x)=5 \quad \Rightarrow \quad -2+x=5 \quad \Rightarrow \quad  x=7

Così unendo gli insiemi delle soluzioni sin qui ottenuti abbiamo per l’equazione con valore assoluto di partenza le soluzioni:

x_1=-3, \qquad x_2 = 7

Consideriamo ora equazioni con valore assoluto della forma:

|P(x)|=f(x)

ove anche {f(x)} è un polinomio. Ora al secondo membro non abbiamo più un numero ma una quantità funzione della {x}.

Applicando la definizione di valore assoluto abbiamo:

P(x)=f(x), \quad \text{per}\: P(x) \geq 0 ; \qquad -P(x)=f(x), \quad \text{per} \: P(x)<0

ovvero:

P(x)=f(x), \quad \text{per} \: P(x) \geq 0 ; \qquad P(x)=-f(x), \quad \text{per} \: P(x) < 0 

Consideriamo ad esempio l’equazione:

|x-2|=3x-1

Abbiamo un’equazione del tipo {|P(x)|=f(x)}. Ragionando come nel caso generale arriviamo alle due equazioni:

x-2=3x-1, \quad \text{per} \: x-2 \geq 0; \qquad -(x-2)=3x-1, \quad \text{per} \: x-2 < 0

ovvero:

x-2=3x-1, \quad \text{per} \: x-2 \geq 0; \qquad x-2=-3x+1, \quad \text{per} \: x-2 < 0

e quindi:

2x=-1, \qquad \text{per} \: x \geq 2; \qquad 4x=3, \qquad \text{per}  \: x< 2

Per maggior chiarezza possiamo esprimere quanto appena scritto utilizzando i sistemi:

\begin{cases} 2x=-1 \\ \\ x \geq 2 \end{cases}; \qquad \begin{cases} 4x=3 \\ \\ x < 2\end{cases}

Così le soluzioni di ciascuna equazione dovranno rispettare la disuguaglianza presente nel corrispondente sistema. Cominciamo risolvendo la prima equazione:

2x=-1 \quad \Rightarrow \quad x=-\dfrac{1}{2} \qquad \text{non accettabile}

La soluzione è non accettabile poiché non rispetta la condizione {x \geq 2}. In altre parole il valore {x=-\dfrac{1}{2}} è soluzione soltanto dell’equazione {2x=-1} ma non è soluzione dell’equazione con valore assoluto di partenza. Si tratta quindi di una soluzione estranea.

Importante. Prestiamo sempre attenzione alle condizioni per le quali è valida ciascuna equazione, confrontando sempre la soluzione ottenuta con la condizione di validità dell’equazione.

Veniamo ora alla seconda equazione:

4x=3 \quad \Rightarrow \quad x=\dfrac{3}{4}, \qquad \text{OK}

La soluzione è accettabile poiché rispetta la condizione presente nel corrispondente sistema, ovvero {x < 2} (infatti {3/4 = 0,75<2}).

Così in conclusione l’equazione con valore assoluto di partenza ammette la soluzione {x=\dfrac{3}{4}}.

Proseguiamo questa semplice introduzione alle equazioni con valore assoluto considerando equazioni del tipo:

|f(x)|=|g(x)|

Osserviamo che se due numeri sono uguali in valore assoluto, allora i due numeri sono uguali o sono opposti. Infatti ad esempio i due numeri {2} e {2} sono uguali tra loro e sono uguali anche in valore assoluto (infatti {|2|=|2|}). Inoltre i numeri {5} e {-5} sono tra loro opposti ma comunque uguali in valore assoluto (infatti {|5|=|-5|}).

Di conseguenza per risolvere l’equazione data basterà unire tra loro gli insiemi delle soluzioni delle due equazioni:

f(x)=g(x); \qquad f(x)=-g(x)

le quali comprendono rispettivamente il caso che le quantità {f(x)} e {g(x)} siano uguali oppure opposte.

Formalmente possiamo utilizzare l’operatore di disgiunzione logica inclusiva:

f(x)=g(x) \quad \vee \quad f(x)=-g(x)

esprimendo il fatto che può valere indifferentemente la prima uguaglianza oppure la seconda, considerando quindi come detto l’unione dei rispettivi insiemi delle soluzioni.

Consideriamo ad esempio l’equazione:

|x+5|=|2x-3|

Per quanto detto possiamo scrivere:

x+5=2x-3 \quad \vee \quad x+5=-(2x-3)

ovvero:

x+5=2x-3 \quad \vee \quad x+5=-2x+3

Risolvendo la prima equazione abbiamo:

x+5-2x+3=0 \quad \Rightarrow \quad -x=-8 \quad \Rightarrow \quad \boxed{x=8}

Risolvendo la seconda equazione:

x+5+2x-3=0 \quad \Rightarrow \quad 3x+2=0 \quad \Rightarrow \quad \boxed{x=-\dfrac{2}{3}}

Considerando l’unione degli insiemi delle soluzioni ottenuti abbiamo per l’equazione con valore assoluto di partenza le soluzioni:

x=8 \quad \vee \quad x=-\dfrac{2}{3}

Caso generale

Vediamo ora come ragionare di fronte ad equazioni con valore assoluto di tipo più generale rispetto ai casi sinora visti. Osserviamo anzitutto che per alcune equazioni è possibile ricondursi ai casi sinora visti con delle semplici manipolazioni algebriche. Ad esempio data l’equazione:

|3x^2-x|+3=0

è sufficiente portare al secondo membro il termine noto in modo da ricondursi all’equazione:

|3x^2-x|=-3

che è della forma {|P(x)|=k} già vista in precedenza. Inoltre, data ad esempio l’equazione:

|x^2-4x|-x^2-1=0

trasportando al secondo membro i termini che non sono all’interno del simbolo di modulo abbiamo:

|x^2-4x|=x^2+1

Ci siamo così ricondotti ad un’equazione della forma {|P(x)|=f(x)}. In altri casi in modo del tutto simile sarà infine possibile ricondursi ad equazioni della forma |f(x)|=|g(x)|.

Tuttavia, consideriamo ora l’equazione:

|2-3x|+|x-1|=2-x

L’equazione non è riconducibile a nessuna delle forme sin qui viste. In casi come questi dobbiamo capire come ragionare nel modo più generale, ovviamente sempre tenendo conto della definizione di modulo o valore assoluto.

L’idea è quella di capire per quali intervalli della {x} ciascuna delle quantità all’interno del simbolo di modulo è positiva o negativa. Per fare questo occorre studiare il segno delle quantità {2-3x} e {x-1}.

Osserviamo che la quantità {2-3x} è positiva per {-3x>-2}, ovvero per {x < \dfrac{2}{3}}. Invece, la quantità {x-1} è positiva per {x > 1}.

Ora, per la definizione di modulo ciò significa che potremo sostituire la quantità {|2-3x|} con la quantità {2-3x} per {x < \dfrac{2}{3}}, e con la quantità {-(2-3x)=-2+3x} per {x \geq \dfrac{2}{3}}. Allo stesso modo, potremo sostituire la quantità {|x-1|} con {x-1} per {x \geq 1}, e con {-(x-1)=-x+1} per {x < 1}.

Così, quello che dobbiamo fare è studiare il segno delle quantità dentro ai simboli di valore assoluto utilizzando un diagramma:

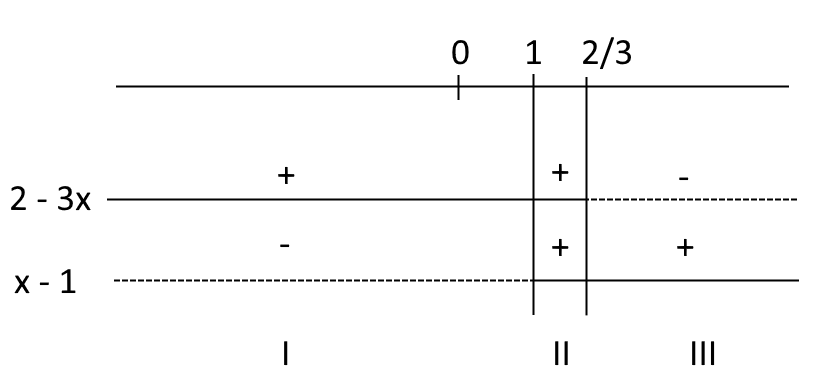
Il diagramma mostra il segno delle quantità {2-3x} e {x-1} negli intervalli di valori assunti dalla {x}. In particolare:

• nell’intervallo {x \leq 1} la quantità {2-3x} è positiva mentre la quantità {x-1} è negativa o al più nulla;
• nell’intervallo {1<x \leq \dfrac{2}{3}} entrambe le quantità risultano positive. La quantità {2-3x} potrà tutt’al più essere nulla;
• infine, nell’intervallo {x > \dfrac{2}{3}} la quantità {2-3x} è negativa mentre la quantità {x-1} è positiva.

Ora, dato che il valore assoluto forza positiva una quantità, è chiaro che potremo sostituire ad esempio all’espressione {|2-3x|} la quantità {2-3x} in un intervallo della {x} in cui la quantità {2-3x} è positiva, e quindi ad esempio nell’intervallo {x \leq 1}. E dato che in questo intervallo la quantità {x-1} è invece negativa, potremo sostituire in questo stesso intervallo all’espressione {|x-1|} la quantità {-(x-1)=-x+1}. Infatti, se la quantità {x-1} è negativa in tale intervallo, la quantità ad essa opposta sarà certamente positiva. E quindi rispettiamo il fatto che il valore assoluto restituisce una quantità sempre positiva.

Così, ragionando in questo modo nei vari intervalli di valori assunti dalla {x}, l’equazione di partenza avrà come insieme delle soluzioni l’unione degli insiemi delle soluzioni dei seguenti sistemi:

\scriptsize \begin{cases}2-3x+(-x+1)=2-x \\ \\ x \leq 1 \end{cases} \qquad \begin{cases}2-3x+x-1=2-x \\ \\  1 < x \leq \dfrac{2}{3}  \end{cases} \qquad \begin{cases}  -2+3x+x-1=2-x \\ \\ x>\dfrac{2}{3}  \end{cases} 

ovvero:

\scriptsize \begin{cases} 2-3x-x+1-2+x = 0\\ \\ x \leq 1\end{cases} \qquad \begin{cases}2-3x+x-1-2+x=0 \\ \\  1 < x \leq \dfrac{2}{3} \end{cases} \qquad \begin{cases}-2+3x+x-1-2+x=0 \\ \\ x > \dfrac{2}{3} \end{cases}

e quindi:

\begin{cases} x = \dfrac{1}{3} \\ \\ x \leq 1\end{cases}; \qquad \begin{cases}x = -1 \\ \\   1 < x \leq \dfrac{2}{3} \end{cases}; \qquad  \begin{cases}x = 1 \\ \\ x > \dfrac{2}{3} \end{cases}

Il secondo sistema è impossibile mentre gli altri due sono determinati ed in conclusione per l’equazione con valore assoluto di partenza abbiamo le soluzioni {x=\dfrac{1}{3}} e {x=1}.

Conclusioni

Per quanto riguarda la definizione di valore assoluto ed una prima introduzione alle equazioni con valori assoluti (equazioni con modulo) è tutto. Se avete incontrato difficoltà nel comprendere le equazioni con valori assoluti nessun problema. Nella prossima lezione ci occuperemo infatti più nel dettaglio delle equazioni con valori assoluti, mostrando vari esempi. Buon proseguimento allora con SìMatematica!