Diagonale di un rettangolo

 - 

Domande e risposte

Quale è la definizione di diagonale di un rettangolo e come si calcola? Quali formule si possono utilizzare per calcolare la diagonale di un rettangolo?

La diagonale di un rettangolo è un segmento che unisce tra loro due vertici non consecutivi del rettangolo. Le diagonali in un rettangolo sono due, entrambe aventi la stessa misura (ovvero, entrambe congruenti). In parole povere, le due diagonali di un rettangolo condividono la stessa lunghezza.

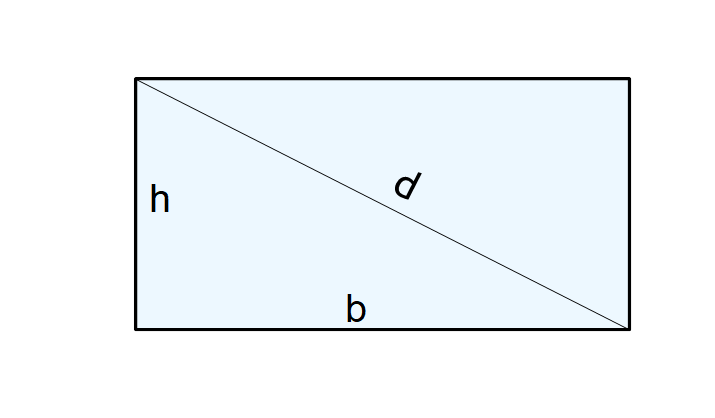
La misura delle diagonali di un rettangolo si calcola estraendo la radice quadrata della somma dei quadrati rispettivamente della base e dell’altezza del rettangolo stesso. In altre parole, la lunghezza di una diagonale del rettangolo si ottiene sommando il quadrato della base con il quadrato dell’altezza, quindi estraendo la radice quadrata del risultato ottenuto.

La formula per il calcolo della lunghezza della diagonale del rettangolo (una delle due diagonali) è la seguente:

d=\sqrt{b^2+h^2}

La formula trae origine dal teorema di Pitagora. Infatti, un rettangolo può essere visto come l’unione di due triangoli rettangoli, aventi per cateti la base e l’altezza del rettangolo e aventi per ipotenusa proprio la diagonale del rettangolo stesso.

E possibile ricavare la misura della diagonale di un rettangolo (misura di una delle due diagonali) a partire dai seguenti dati:

• base ed altezza del rettangolo (utilizzando la formula appena vista);
• area e base del rettangolo oppure area ed altezza del rettangolo;
• perimetro e base oppure perimetro ed altezza del rettangolo. In alternativa al posto del perimetro può anche essere dato il semiperimetro.

Con riferimento al secondo e al terzo punto, l’idea è quella di ricavare dai dati disponibili la misura della dimensione mancante (base o altezza), e quindi ricavare la misura delle diagonali utilizzando la stessa formula che abbiamo dato in precedenza. Per fare questo dovremo ragionare con la formula dell’area del rettangolo o con la formula del perimetro e del semiperimetro del rettangolo. Ricordiamo le due formule, indicando con {A} l’area del rettangolo, con {p} il perimetro e con {\dfrac{p}{2}} il semiperimetro:

A=b \cdot h, \qquad p=2 \cdot (b+h), \qquad \dfrac{p}{2}=b+h

Attenzione: alcune notazioni indicano invece con {2p} il perimetro e con {p} il semiperimetro. Prestate dunque per favore attenzione alle notazioni utilizzate dal vostro libro e/o insegnante.

Vediamo subito degli esempi relativi al calcolo della lunghezza della diagonale del rettangolo (più precisamente, calcolo della misura delle diagonali del rettangolo).

Esempio 1

Calcolare la misura {d} delle diagonali di un rettangolo avente base {b=4 \text{cm}} e altezza {h=3 \text{cm}} .

Abbiamo:

\begin{align*} & d = \sqrt{b^2+h^2}=\sqrt{(4 \text{cm})^2+(3 \text{cm})^2}= \\ \\ & = \sqrt{(16+9) \text{cm}^2}= \sqrt{25 \text{cm}^2}= 5 \text{cm} \end{align*}

Esempio 2

Calcolare la misura delle diagonali di un rettangolo di area {48 \text{m}^2} e avente base {8\text{m}}.

Se disponiamo dell’area e della misura di una dimensione di un rettangolo, possiamo ricavare la dimensione mancante dividendo l’area per la dimensione che ci viene fornita nel testo. Così, dato che abbiamo l’area e la misura della base possiamo ricavare la misura dell’altezza come segue:

h = \dfrac{A}{b}=\dfrac{48 \text{m}^2}{8 \text{m}}=6 \text{m}

A questo punto possiamo ricavare la misura delle diagonali poiché abbiamo tutte e due le dimensioni del rettangolo:

\begin{align*} & d = \sqrt{b^2+h^2}= \sqrt{(8 \text{m})^2 + (6 \text{m})^2} = \\ \\ & = \sqrt{64 \text{m}^2 + 36 \text{m}^2 }= \sqrt{100 \text{m}^2}= 10 m \end{align*}

Esempio 3

Vediamo un ultimo esempio sul calcolo della diagonale di un rettangolo a partire dal perimetro e dalla misura dell’altezza.

Calcolare la diagonale di un rettangolo avente perimetro {42 \text{cm}} e altezza {9 \text{cm}}.

Osserviamo che il semiperimetro è la somma delle misure della base e dell’altezza. Ricaviamo anzitutto il semiperimetro a partire dal perimetro:

\dfrac{p}{2}=p:2 = 42 \text{cm} : 2 = 21 \text{cm}

A questo punto ricaviamo la misura della base come differenza del semiperimetro e della misura dell’altezza:

b = \dfrac{p}{2}-h=21 \text{cm} - 9 \text{cm} = 12 \text{cm}

A questo punto avendo sia la base, sia l’altezza possiamo calcolare la misura delle diagonali:

\begin{align*} & d = \sqrt{b^2+h^2}=\sqrt{12^2 \text{cm}^2+9^2 \text{cm}^2}= \\ \\ & =\sqrt{144 \text{cm}^2 + 81 \text{cm}^2} = \sqrt{225 \text{cm}^2}=15 \text{cm} \end{align*}