Le disequazioni di secondo grado sono particolari disequazioni algebriche che, una volta ridotte in forma normale, si presentano alternativamente come:
P(x) <0; \quad P(x) \leq 0; \quad P(x) > 0; \quad P(x) \geq 0
con {P(x)} polinomio di secondo grado.
Le disequazioni di secondo grado possono essere risolte utilizzando la tecnica delle disequazioni prodotto oppure mediante il metodo della parabola, il quale tratteremo nel dettaglio proprio in questa lezione.
La tecnica relativa alle disequazioni prodotto consiste nello scomporre il polinomio {P(x)} al primo membro della disequazione di secondo grado in forma normale nel prodotto di due polinomi di primo grado. Fatto questo sarà possibile studiare il segno del prodotto dei polinomi, determinando di conseguenza l’insieme delle soluzioni della disequazione data.
Il metodo della parabola per le disequazioni di secondo grado si basa invece sull’osservare che la funzione:
f(x)=ax^2+bx+c, \quad a, \: b, \: c \in \mathbb{R}rappresenta una parabola, la quale avrà concavità rivolta verso l’alto o verso il basso in base al segno del coefficiente {a}. L’idea in particolare è quella di rappresentare graficamente la parabola, osservare dove il grafico si trova al di sopra e al di sotto dell’asse delle {x} e quindi individuare di conseguenza l’insieme delle soluzioni della disequazione di secondo grado.
Il punto di partenza per l’utilizzo del metodo della parabola, come vedremo, è dato dal risolvere l’equazione di secondo grado associata:
ax^2+bx+c=0
I ragionamenti cambieranno in base al fatto che l’equazione ammetta due soluzioni reali e distinte, due soluzioni reali e coincidenti oppure nessuna soluzione reale.
Precisiamo inoltre che per comprendere il metodo della parabola è ovviamente necessario avere presenti le equazioni di secondo grado. La loro conoscenza non è invece necessaria se si utilizza il metodo delle disequazioni prodotto.
Fatte le dovute premesse, vediamo subito come risolvere le disequazioni di secondo grado.
Disequazioni di secondo grado come disequazioni prodotto (metodo algebrico)
Consideriamo una generica disequazione di secondo grado in forma normale, ovvero:
P(x) \lesseqgtr0
con {P(x)} polinomio di secondo grado. Il simbolo {\lesseqgtr} rappresenta un generico simbolo di disuguaglianza, che in un caso concreto sarà maggiore, oppure minore, ecc…
Se la disequazione non si presenta in forma normale, sarà comunque possibile ricondurla alla forma normale utilizzando le proprietà delle disequazioni.
Nelle disequazioni prodotto, l’idea è quella di scomporre il polinomio {P(x)} nel prodotto di due polinomi {P_1(x)} e {P_2(x)}, entrambi di primo grado.
Consideriamo ad esempio la disequazione:
x^2+3x-10 > 0
La disequazione si presenta già in forma normale, infatti è del tipo {P(x) > 0} con {P(x)=x^2+3x-10}. Inoltre, poiché {P(x)} è di secondo grado, abbiamo una disequazione di secondo grado.
Scomponiamo {P(x)} utilizzando ad esempio la tecnica di scomposizione del trinomio caratteristico. In alternativa precisiamo che è anche possibile effettuare la scomposizione sfruttando le soluzioni dell’equazione {P(x)=0} (vedi scomposizione in fattori con le equazioni di secondo grado).
Utilizzando il metodo del trinomio caratteristico, abbiamo:
x^2+3x-10 =(x-2)(x+5)
Di conseguenza la disequazione di partenza diviene:
(x-2)(x+5) > 0
Ora, come visto per le disequazioni prodotto, si tratterà di studiare il segno di ciascun fattore al primo membro nello stesso diagramma:
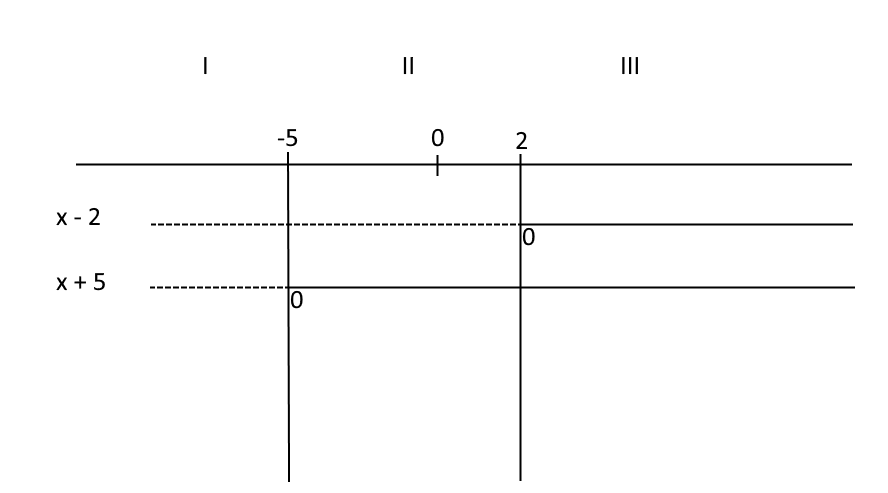
Nel diagramma abbiamo individuato tre intervalli di valori della {x}, ciascuno indicato con un numero romano.
Ora, per ciascun intervallo determiniamo il segno del prodotto {(x-2)(x+5)}. Per fare questo basta applicare l’algebra dei segni ad ogni intervallo.
Ad esempio, nel primo intervallo entrambi i fattori sono negativi (linea tratteggiata). Così, il loro prodotto avrà come segno il più (infatti, meno per meno dà più). Così in pratica dobbiamo moltiplicare tra loro i segni dei fattori per ciascun intervallo.
Procedendo in questo modo otteniamo per il prodotto i seguenti segni:
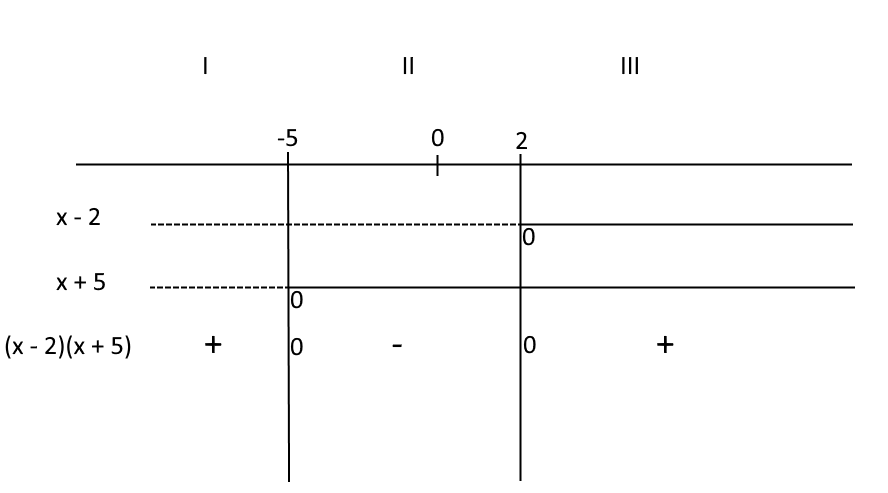
A questo punto per risolvere la disequazione basta ragionare sui segni del prodotto che abbiamo appena determinato. In particolare, poiché abbiamo la disequazione
(x-2)(x+5) > 0
dovremo prendere come soluzioni i soli valori della x per i quali il prodotto è positivo. Infatti come è immediato osservare la disequazione da risolvere richiede che il prodotto {(x-2)(x+5)} sia positivo.
Completando il diagramma, per l’insieme delle soluzioni della disequazione data abbiamo quindi:
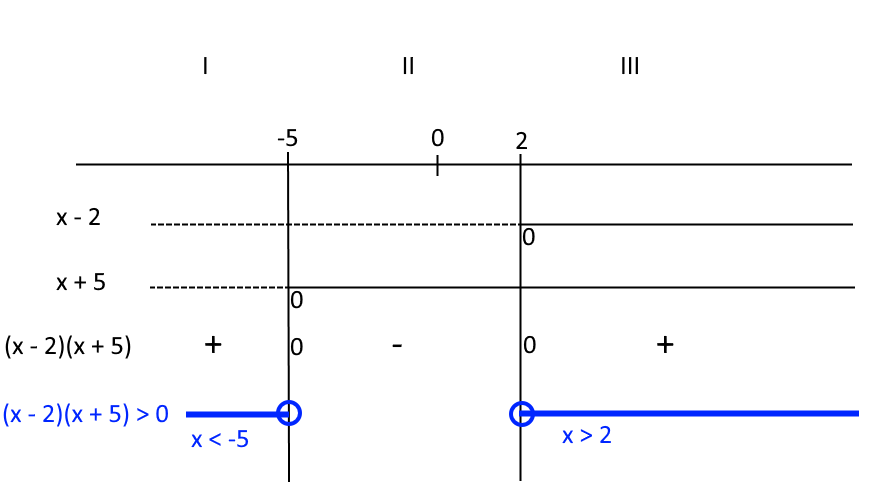
Abbiamo così preso gli intervalli ove il prodotto {(x-2)(x+5)} è positivo. Abbiamo invece escluso i valori {x=-5} e {x = 2} poiché in essi il prodotto si annulla. Ed effettivamente nella disequazione abbiamo il simbolo di “maggiore” e non “maggiore o uguale”. Dunque tali valori vanno esclusi poiché rendono uguali tra loro i due membri della disequazione, e data la presenza di un simbolo di maggiore stretto (che non comprende cioè l’uguale), tale uguaglianza non è ammessa.
Di conseguenza, per la disequazione assegnata abbiamo in conclusione l’insieme delle soluzioni:
x < -5 \quad \vee \quad x > 2
ove il simbolo “{\vee}” indica “oppure”.
Il metodo appena visto per risolvere le disequazioni di secondo grado è conosciuto anche con il nome di metodo algebrico. Effettivamente, come visto il metodo si basa sull’utilizzo dell’algebra dei segni.
Disequazioni di secondo grado con il metodo della parabola
Il metodo della parabola consente di individuare rapidamente il segno assunto dal polinomio di secondo grado {P(x)} ragionando sulla parabola relativa alla funzione {f(x)=P(x)}. Basta infatti tener presente che la parabola di equazione:
y=P(x), \quad \text{con} \: P(x) \: \text{di secondo grado}ovvero
y=ax^2+bx+c, \quad \text{con} \quad a, \: b, \: c \in \mathbb{R}starà al di sopra dell’asse delle x per valori esterni agli zeri di P(x) se il coefficiente {a} è positivo. Se invece il coefficiente {a} è negativo, la parabola si troverà al di sopra dell’asse delle x per valori interni agli zeri di P(x).
Quanto appena detto risulterà immediatamente chiaro osservando la seguente figura:
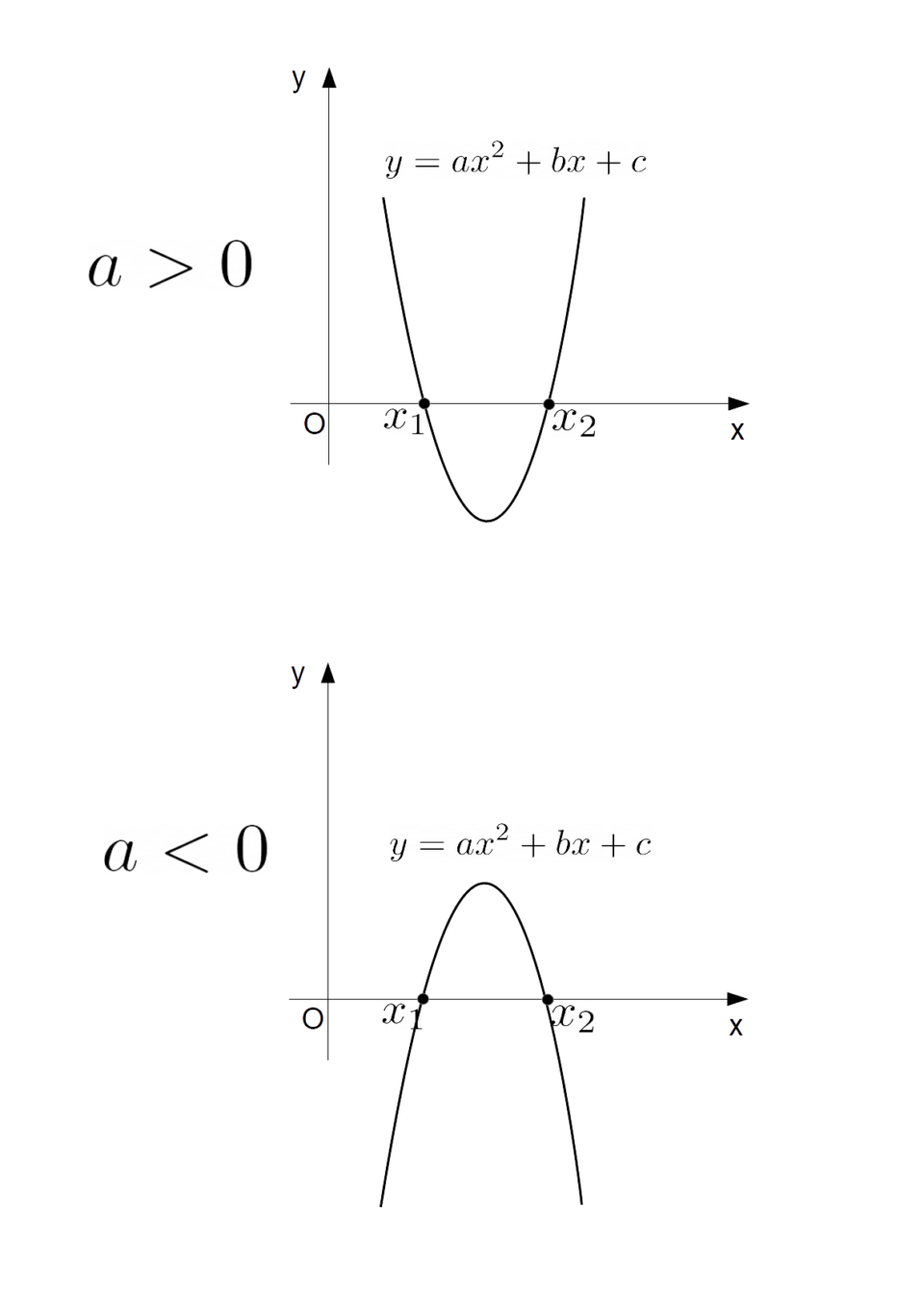
Se il coefficiente {a} è positivo, la concavità della parabola è rivolta verso l’alto. In altre parole, immaginando la parabola come un bicchiere pieno d’acqua, se il coefficiente {a} è positivo, l’acqua rimane all’interno del bicchiere.
Se invece il coefficiente {a} è negativo, la concavità della parabola è rivolta verso il basso. In altri termini, ancora immaginando la parabola come un bicchiere pieno d’acqua, se il coefficiente {a} è negativo, l’acqua cade dal bicchiere.
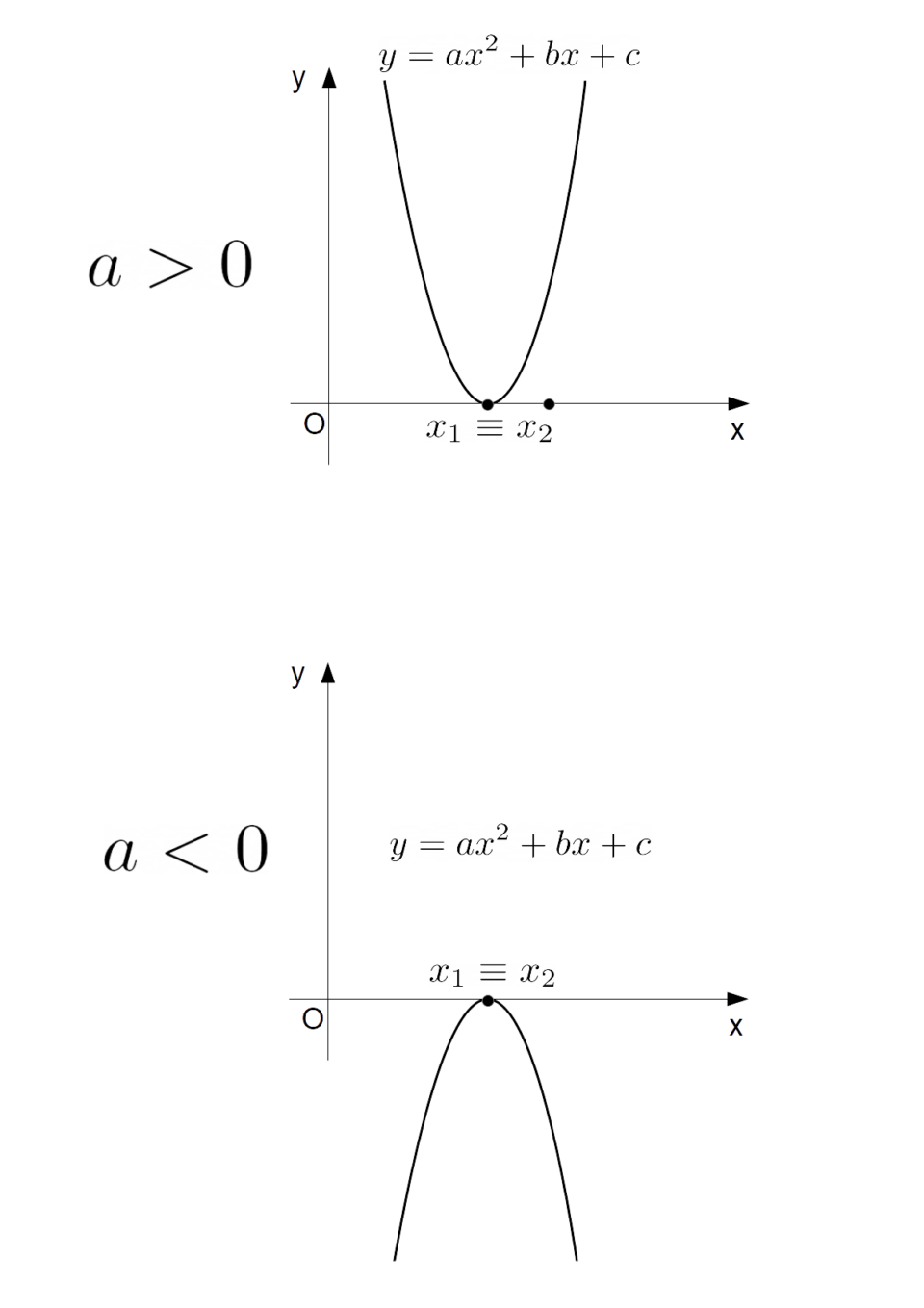
Ora, osserviamo che le quantità {x_1} e {x_2} sono gli zeri del polinomio {P(x)}, ovvero le soluzioni dell’equazione di secondo grado associata {ax^2+bx+c=0}, che nei casi appena visti supponiamo determinata con due soluzioni reali e distinte.
Se invece l’equazione di secondo grado associata ha due soluzioni reali coincidenti, la parabola {y=ax^2+bx+c} intersecherà l’asse delle {x} in un solo punto. E altrove il suo grafico risulterà sopra l’asse delle {x} se il coefficiente {a} è positivo, sotto l’asse delle {x} se il coefficiente {a} è negativo.
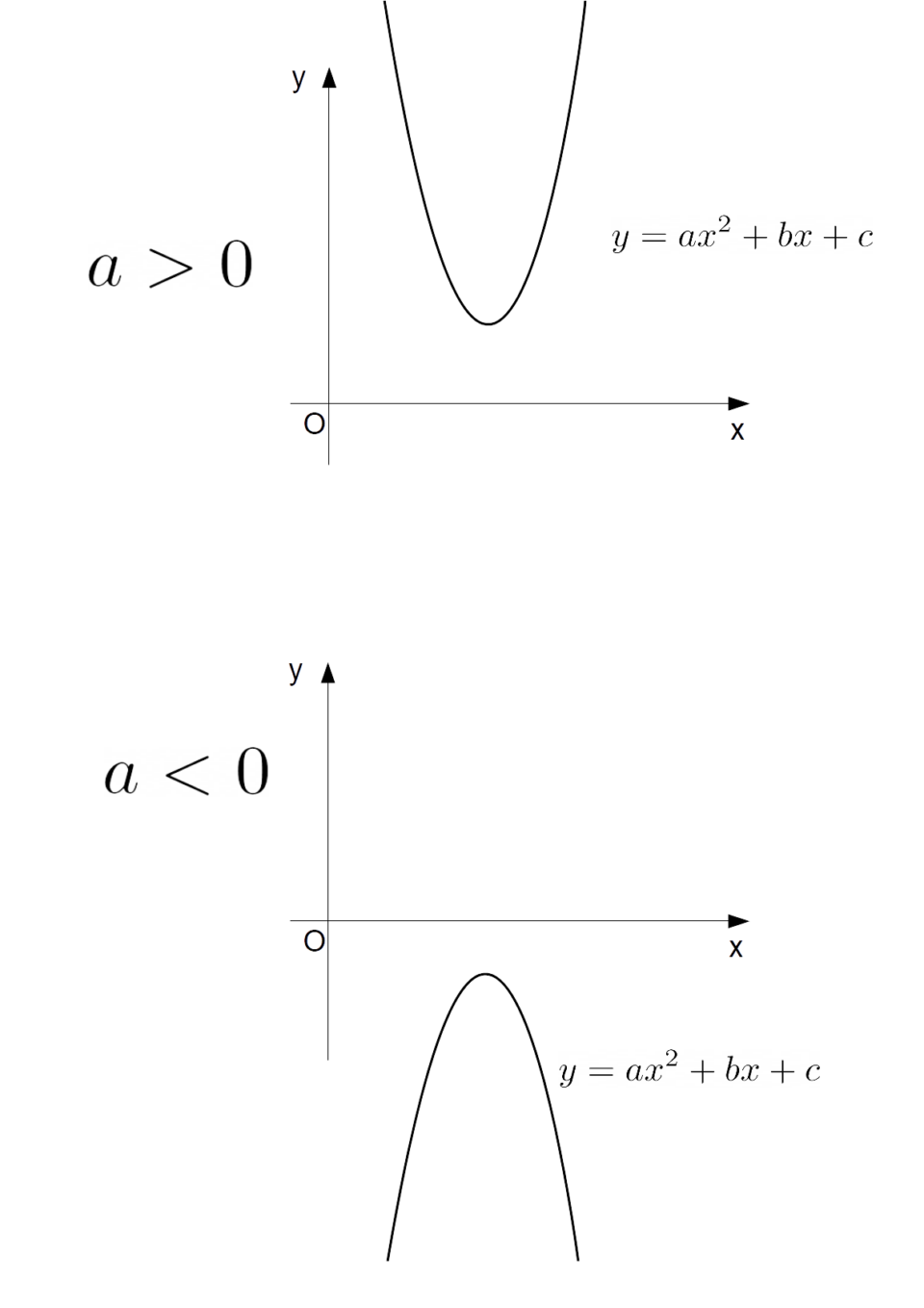
Infine, se l’equazione associata non ammette soluzioni reali, la parabola non avrà alcun punto di intersezione con l’asse delle {x}, e risulterà sempre al di sopra di tale asse se il coefficiente {a} è positivo, e sempre al di sotto di tale asse se il coefficiente {a} è, invece, negativo.
Ora, le considerazioni fatte sulla parabola {y=ax^2+bx+c} si riflettono ovviamente sul segno del polinomio {ax^2+bx+c}. In particolare:
- se l’equazione {ax^2+bx+c=0} è determinata con due soluzioni reali e distinte, se il coefficiente {a} è positivo il polinomio {ax^2+bx+c} sarà positivo per valori esterni agli zeri dell’equazione. Diversamente, se il coefficiente {a} è negativo, il polinomio sarà positivo per valori interni agli zeri;
- se l’equazione {ax^2+bx+c=0} è determinata con due soluzioni reali e coincidenti, se il coefficiente {a} è positivo il polinomio {ax^2+bx+c} sarà positivo per tutti i valori della {x} tranne gli zeri. Invece, se il coefficiente {a} è negativo il polinomio sarà negativo per tutti i valori della {x} tranne gli zeri. Ovviamente, negli zeri il polinomio sarà nullo;
- infine, se l’equazione {ax^2+bx+c=0} è indeterminata (ovvero non ha soluzioni reali), il polinomio {ax^2+bx+c} sarà o sempre positivo o sempre negativo se rispettivamente il coefficiente {a} è positivo o negativo. Con il termine “sempre” intendiamo per ogni valore della {x}.
Così, pensando alla parabola {y=ax^2+bx+c}, possiamo studiare rapidamente il segno del polinomio {ax^2+bx+c} una volta note le eventuali soluzioni reali dell’equazione {ax^2+bx+c=0}. E proprio in base al segno del polinomio {ax^2+bx+c} potremo determinare l’insieme delle soluzioni della disequazione di secondo grado da risolvere. Infatti, una volta ridotta alla forma normale, una disequazione di secondo grado richiede semplicemente che un polinomio del tipo {ax^2+bx+c} sia positivo oppure negativo (eventualmente anche nullo). E l’insieme delle soluzioni della disequazione sarà dato dai valori della {x} che verificano quanto richiesto.
Di conseguenza, per risolvere una disequazione di secondo grado con il metodo della parabola occorre:
- determinare le eventuali soluzioni reali {x_1, \: x_2} dell’equazione associata {ax^2+bx+c=0};
- chiedersi se il segno del coefficiente {a} è positivo oppure negativo;
- se {x_1, \:x_2} esistono e sono diversi tra loro, ed inoltre il coefficiente {a} è positivo, il polinomio {ax^2+bx+c} sarà positivo per {x < x_1 \quad \vee \quad x > x_2}, e sarà negativo per { x_1 < x < x_2}. Così, se la disequazione da risolvere è del tipo {ax^2+bx+c > 0}, questa sarà verificata per {x < x_1 \quad \vee \quad x > x_2} (valori esterni agli zeri). Invece, se la disequazione è del tipo {ax^2+bx+c < 0}, questa sarà verificata per {x_1< x < x_2 } (valori della {x} interni agli zeri). E ragionando in modo del tutto simile sarà inoltre possibile trarre le opportune conclusioni nel caso in cui il coefficiente {a} sia negativo;
- se {x_1, \: x_2} esistono ma sono tra loro coincidenti, se il coefficiente {a} è positivo, il polinomio sarà positivo per tutti i valori della {x} tranne gli zeri. Diversamente, se il coefficiente {a} è negativo il polinomio sarà negativo per tutti i valori della {x} tranne gli zeri. Così ad esempio la disequazione {ax^2+bx+c > 0}, se {a} è positivo, risulterà soddisfatta per tutti i valori reali della {x} tranne gli zeri, mentre la stessa disequazione {ax^2+bx+c>0} ma con {a} negativo risulterà impossibile (non verificata per nessun valore reale della {x});
- infine, se gli zeri (reali) del polinomio non esistono (equazione {ax^2+bx+c=0} impossibile), allora il polinomio {ax^2+bx+c} risulterà rispettivamente sempre positivo o sempre negativo a seconda che il coefficiente {a} sia positivo o negativo. Di conseguenza, se {a} è positivo la disequazione {ax^2+bx+c>0} sarà soddisfatta per ogni valore reale (disequazione indeterminata). Diversamente, sempre con {a} positivo, la disequazione {ax^2+bx+c<0} sarà impossibile (ovvero non verificata per nessun valore della {x}). Considerazioni del tutto simili valgono nel caso di coefficiente {a} negativo.
Va inoltre sottolineato che se nella disequazione da risolvere è presente il simbolo di “minore o uguale” oppure il simbolo di “maggiore o uguale”, gli eventuali zeri dell’equazione associata {ax^2+bx+c=0} dovranno essere compresi nell’insieme delle soluzioni della disequazione.
Vediamo subito degli esempi.
Esempio 1 (metodo della parabola)
Risolvere la seguente disequazione di secondo grado:
x^2+x-12 > 0
Abbiamo una disequazione del tipo {ax^2+bx+c > 0}, quindi già in forma normale, con {a=1} positivo. La parabola {y=x^2+x-12} ha quindi concavità verso l’alto, e il suo grafico si troverà al di sopra dell’asse delle {x} per valori esterni agli eventuali zeri dell’equazione di secondo grado associata {x^2+x-12=0}.
Risolviamo allora l’equazione associata:
\small x^2+x-12 > 0 \quad \Rightarrow \quad x_{1,2}=\dfrac{-1 \pm \sqrt{1^2-4 \cdot 1 \cdot (-12)}}{2}=\begin{cases}-4 \\ \\ 3 \end{cases}Così la parabola starà al di sopra dell’asse delle x per {x < -4} e per {x>3}. E in particolare per tali valori il polinomio {x^2+x-12} risulterà positivo. E dato che la disequazione di partenza richiede che detto polinomio sia positivo, l’insieme delle soluzioni della disequazione è individuato dalle condizioni:
x < -4 \quad \vee \quad x > 3
Esempio 2
Risolvere la seguente disequazione di secondo grado:
x^2-12x+20 \leq 0
Anche in questo caso ci ritroviamo con una disequazione di secondo grado in forma normale.
La disequazione richiede che il polinomio al primo membro sia minore o al più uguale a zero.
Osserviamo che il coefficiente {a} è positivo. Siamo quindi nel caso di parabola con concavità rivolta verso l’alto. Dunque il polinomio sarà positivo per valori della {x} esterni agli eventuali zeri dell’equazione associata e negativo per i valori ad essi interni. Inoltre il polinomio sarà nullo in corrispondenza degli zeri.
Risolviamo a questo punto l’equazione associata:
x^2-12x+20=0
otteniamo le soluzioni:
x_1 = 2, \qquad x_2 = 10
Ora confrontiamo quanto sappiamo sui segni del polinomio al primo membro con la richiesta della disequazione. Dato che la disequazione richiede che il polinomio sia negativo o nullo, avremo l’insieme delle soluzioni:
2\leq x \leq 10
Osserviamo che abbiamo compreso nell’insieme delle soluzioni anche gli zeri. Infatti la disequazione di partenza comprende l’uguaglianza (abbiamo un simbolo di “minore o uguale”).
Conclusioni
Per quanto riguarda le disequazioni di secondo grado è tutto. Per chi vuole allenarsi è anche disponibile la scheda di esercizi correlata (vedi link a seguire). Buon proseguimento con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
