Disequazioni fratte

 - 

Disequazioni algebriche

Le disequazioni fratte (o frazionarie) sono particolari disequazioni nelle quali l’incognita compare anche a denominatore. La tecnica per risolvere disequazioni di questo tipo è molto simile a quella vista per le disequazioni prodotto. Tuttavia, esiste un’importante differenza dovuta proprio alla presenza dell’incognita al denominatore.

In particolare, nelle disequazioni fratte dovremo assicurarci di non includere nell’insieme delle soluzioni quei valori che annullano il denominatore del primo membro della disequazione ridotta in forma normale. E come vedremo, il problema si presenta qualora nella disequazione sia anche ammessa l’uguaglianza tra i due membri. Ci riferiamo quindi alle disequazioni nelle quali compaiono i simboli di “minore o uguale” oppure “maggiore o uguale”.

Così, in presenza dei simboli di “minore” e “maggiore” potremo ragionare in modo del tutto simile a quanto visto per le disequazioni prodotto. Diversamente, dovremo essere certi di escludere i valori della {x} tali da annullare il denominatore o i denominatori presenti nella disequazione. Quest’ultimo ragionamento è esattamente quello visto nel caso delle equazioni fratte di primo grado.

Precisiamo fin da subito che una disequazione fratta in forma normale si presenta come:

\dfrac{N(x)}{D(x)} \lesseqgtr 0

Nelle disequazioni fratte di questa lezione riusciremo sempre a scomporre il numeratore {N(x)} e il denominatore {D(x)} come prodotti fra polinomi di primo grado. In tal modo, potremo sfruttare le nostre conoscenze sulle disequazioni di primo grado.

Disequazioni fratte con disuguaglianze strette

Cominciamo dal caso di disequazioni fratte con disuguaglianze strette, ovvero con disequazioni frazionare che presentano i soli simboli di disuguaglianza “minore” oppure “maggiore”. Ci riferiamo quindi a disequazioni dei due seguenti tipi:

\dfrac{N(x)}{D(x)} > 0; \qquad \dfrac{N(x)}{D(x)} < 0

Per questa lezione le quantità {N(x)} e {D(x)} saranno sempre polinomi di primo grado o comunque polinomi riconducibili a prodotti tra polinomi tutti di primo grado. Comunque, precisiamo che una volta acquisita la conoscenza delle disequazioni di secondo grado (vedi una delle successive lezioni), non sarà più necessario scomporre {N(x)} e {D(x)} in prodotti di polinomi tutti di primo grado. Così in futuro potremo anche lavorare con polinomi di secondo grado, senza preoccuparci se questi possano essere ulteriormente scomposti o meno.

Ora, disequazioni fratte di questo tipo impongono rispettivamente che il rapporto {\dfrac{N(x)}{D(x)}} sia positivo oppure negativo. Ciò dal punto di vista dell’algebra dei segni è la stessa cosa di richiedere che il prodotto {P(x) \cdot D(x) } sia positivo oppure negativo. Di conseguenza, possiamo avvalerci della stessa tecnica utilizzata per le disequazioni prodotto.

Vediamo subito degli esempi su come risolvere le disequazioni fratte.

Esempio 1

Risolvere la seguente disequazione fratta:

\dfrac{5-6x}{6-x} < 2-\dfrac{1}{6-x}

In generale dobbiamo prima di tutto ricondurre una disequazione fratta (in questo caso con disuguaglianza stretta) alla forma normale:

\dfrac{N(x)}{D(x)} \lessgtr 0

ove con il simbolo “{\lessgtr}” intendiamo alternativamente o il simbolo di maggiore o il simbolo di minore. Così nel caso della disequazione in esame dobbiamo ricondurci alla forma:

\dfrac{N(x)}{D(x)} < 0

Cominciamo trasportando tutti i termini al primo membro:

\dfrac{5-6x}{6-x} -2+\dfrac{1}{6-x}<0

Ora mettiamo tutti i termini al primo membro a denominatore comune:

\dfrac{5-6x-2(6-x)+1}{6-x}  < 0 

e quindi:

\dfrac{5-6x-12+2x+1}{6-x}<0

ovvero sommando i termini simili al numeratore:

\dfrac{-4x-6}{6-x}< 0

Lavorando sui segni possiamo anche riscrivere la frazione algebrica al primo membro in altra forma. In particolare, invertendo i segni sia del numeratore, sia del denominatore della frazione algebrica otteniamo:

\dfrac{4x+6}{x-6}<0

A questo punto ci ritroviamo con una disequazione fratta in forma normale. Infatti, la disequazione è della forma {\dfrac{N(x)}{D(x)} < 0 } con {N(x)=4x+6} e {D(x)=x-6}.

Ora, la disequazione è soddisfatta per i valori della {x} tali da rendere il rapporto {\dfrac{4x+6}{x-6}} positivo. Di conseguenza, occorrerà studiare il segno del numeratore e del denominatore in uno stesso diagramma, e quindi ricavare il segno della frazione in base all’algebra dei segni. Ciò equivale, lo sottolineiamo ancora, a studiare il segno del prodotto come nel caso delle disequazioni prodotto.

Effettuiamo lo studio del segno delle quantità {N(x)} e {D(x)}, ottenendo poi grazie all’algebra dei segni lo studio del segno del loro rapporto:

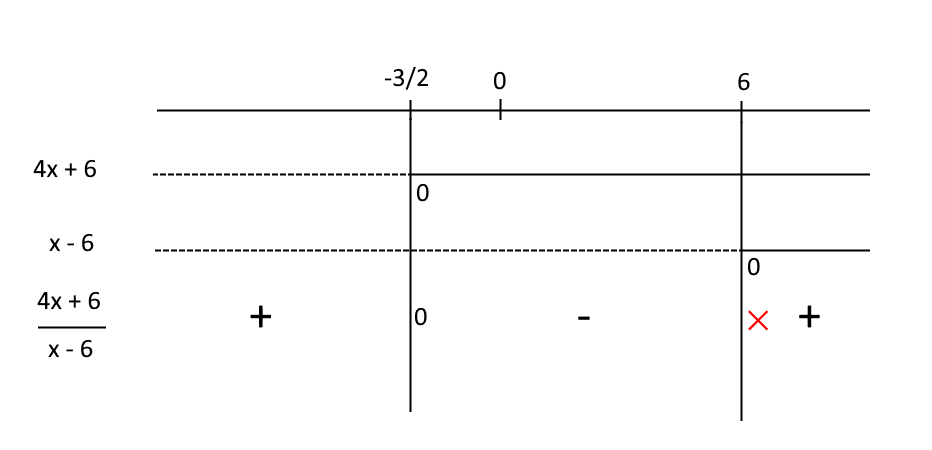
Così sappiamo che il primo membro della disequazione in forma normale è positivo per i valori della {x} minori di {-\dfrac{3}{2}} e maggiori di {6}, è negativo per i valori strettamente compresi tra {-\dfrac{3}{2}} e {6} ed è nullo per il valore {x=-\dfrac{3}{2}}. Tale valore annulla infatti il numeratore.

Ora, attenzione. Il valore {x=-6} annulla il denominatore della frazione e quindi la rende priva di significato. Abbiamo quindi posto una croce rossa in corrispondenza di tale valore.

Fatte queste considerazioni siamo praticamente arrivati. Infatti, la disequazione di partenza richiede che il rapporto al primo membro sia negativo. Saranno quindi soluzioni della disequazione i valori della {x} che rendono negativo il rapporto al primo membro. E poiché vediamo dal diagramma che tali valori sono quelli compresi strettamente tra {-\dfrac{3}{2}} e {6}, la disequazione ha un insieme delle soluzioni individuato dalla condizione:

-\dfrac{3}{2}< x < 6

ovvero, in forma grafica:

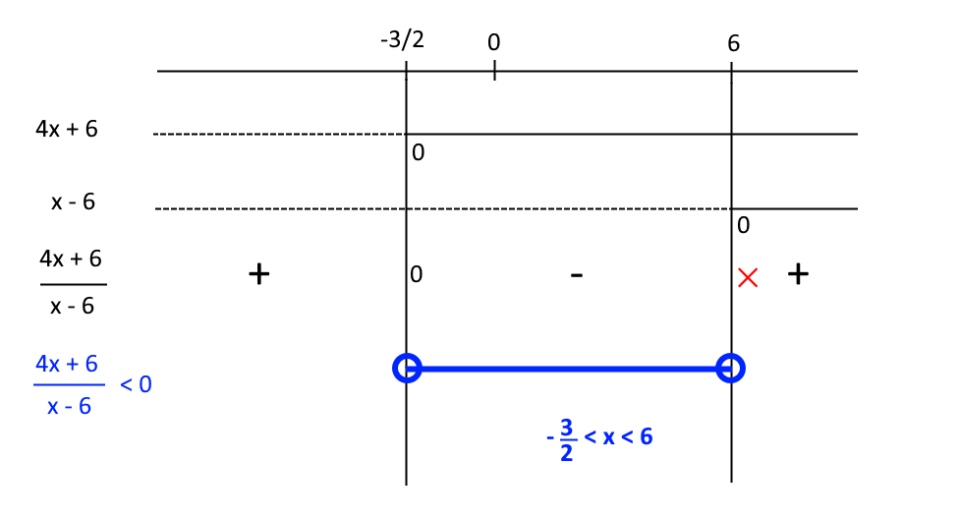
Osserviamo che abbiamo posto in corrispondenza dei valori {-\dfrac{3}{2}} e {6} dei “pallini” vuoti. Infatti, tali valori sono esclusi dall’insieme delle soluzioni della disequazione. E questo, lo sottolineiamo, perché nella disequazione è presente il simbolo di “maggiore” e non “maggiore o uguale”. Dunque, come già visto, non possiamo prendere il valore {-\dfrac{3}{2}} che annulla il numeratore {N(x)}. Inoltre, il valore {6} è escluso poiché annulla il denominatore {D(x)}, rendendo la frazione {\dfrac{N(x)}{D(x)}} priva di significato.

Importante. Con l’espressione “valori compresi strettamente tra {a} e {b}” intendiamo tutti i valori più piccoli di {b} e allo stesso tempo più grandi di {a}, esclusi i valori {a} e {b}.

Esempio 2

Vediamo un ulteriore esempio su come risolvere le disequazioni fratte:

\dfrac{5-x}{-1-x} <  4

Attenzione. Non dimentichiamo prima di tutto di ricondurre la disequazione alla forma normale. Essa non è ancora in forma normale poiché al secondo membro abbiamo un numero diverso da zero.

Portiamo tutto al primo membro:

\dfrac{5-x}{-1-x}-4  <  0

quindi mettiamo tutti i termini al primo membro a denominatore comune:

\dfrac{5-x-4(-1-x)}{-1-x} < 0

e quindi:

\dfrac{5-x+4+4x}{-1-x} < 0

ovvero:

\dfrac{3x+9}{-x-1} <  0

Ora la disequazione fratta si presenta in forma normale. A questo punto studiamo il segno della frazione algebrica al primo membro, per poi individuare gli intervalli in cui è negativa. Infatti, nella disequazione abbiamo il simbolo di “minore”.

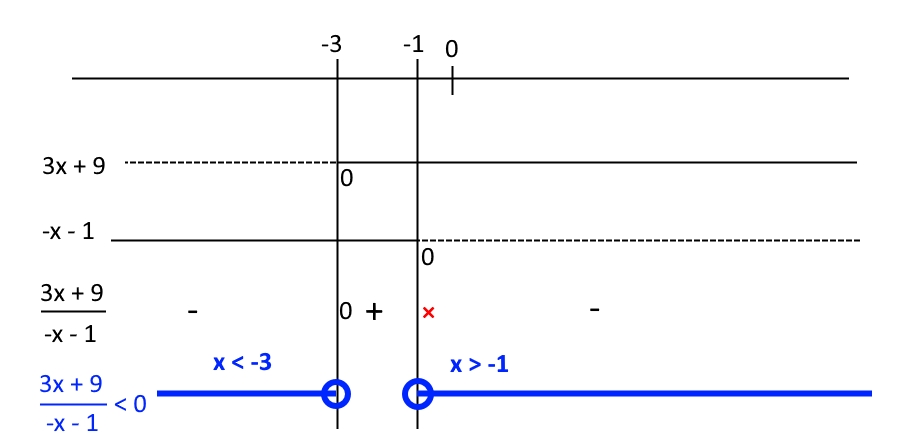
La disequazione di partenza è dunque soddisfatta per:

x < -3 \quad \vee \quad x > -1

ovvero per tutti i valori minori di {-3} e per tutti i valori maggiori di {-1}. I valori {-3} e {-1} sono esclusi dall’insieme delle soluzioni della disequazione. In essa è infatti presente il simbolo di “maggiore”, e non “maggiore o uguale”. Di conseguenza, l’uguaglianza tra i membri della disequazione è esclusa.

Disequazioni frazionarie (fratte) che includono anche l’uguaglianza

Consideriamo ora disequazioni fratte che in forma normale si presentano come:

\dfrac{N(x)}{D(x)} \geq 0; \qquad \dfrac{N(x)}{D(x)} \leq 0 

ovvero disequazioni nelle quali è anche ammessa l’uguaglianza tra i loro membri. I due simboli di disuguaglianza riportati si leggono rispettivamente “maggiore o uguale” e “minore o uguale”. In pratica si tratta di dei simboli di maggiore e minore sottolineati, in modo da indicare che è anche ammessa l’uguaglianza.

In questo caso il metodo risolutivo è molto simile a quanto visto in precedenza, ma con la differenza che saranno soluzioni della disequazione anche i valori dell’incognita che annullano il denominatore.

Dovremo invece escludere i valori della {x} che annullano il denominatore. Infatti, per essi la frazione algebrica {\dfrac{N(x)}{D(x)}} è priva di significato.

Vediamo subito un paio di esempi.

Esempio 3

Risolvere la seguente disequazione:

\dfrac{6+x}{x} \leq 1

Anzitutto riconduciamo la disequazione alla forma normale:

\dfrac{6+x}{x}-1 \leq 0 

ovvero, mettendo i termini a denominatore comune:

\dfrac{6+x-x}{x} \leq 0

ovvero:

\dfrac{6}{x} \leq 0

Studiamo il segno della frazione algebrica a primo membro e determiniamo l’insieme delle soluzioni della disequazione. Osserviamo che il numeratore, essendo un numero, assume sempre lo stesso segno (in questo caso, positivo).

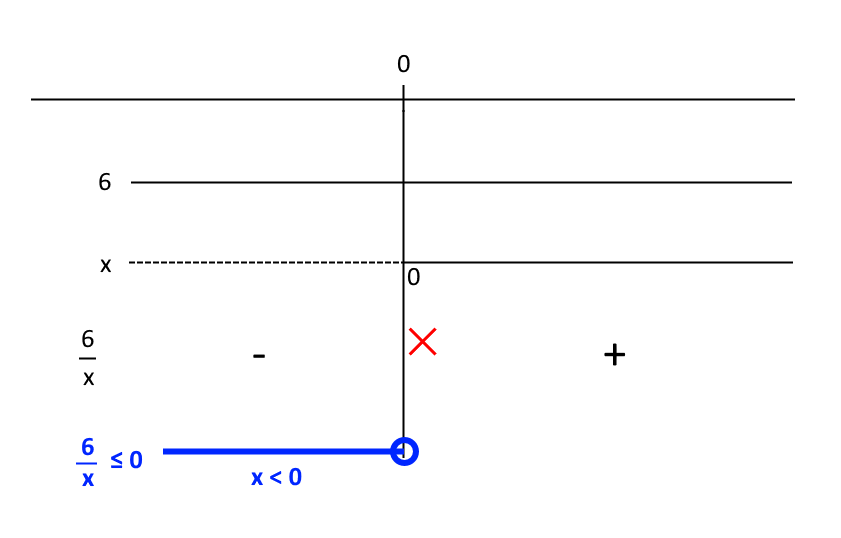
Come possiamo vedere, abbiamo dovuto escludere il valore {0} per la {x}. Infatti, per tale valore si annulla il denominatore della frazione. Inoltre, non esiste alcun valore che annulla il numeratore della frazione. Di conseguenza la disequazione è soddisfatta per:

x < 0

Esempio 4

Consideriamo la seguente disequazione fratta:

\dfrac{5+4x}{x} \geq 1 

Come al solito, riconduciamo la disequazione alla forma normale:

\small \dfrac{5+4x}{x}-1 \geq 0; \qquad \dfrac{5+4x-x}{x} \geq 0 ; \qquad \dfrac{3x+5}{x} \geq 0

Studiamo il segno della frazione algebrica a primo membro ed individuiamo l’insieme delle soluzioni della disequazione:

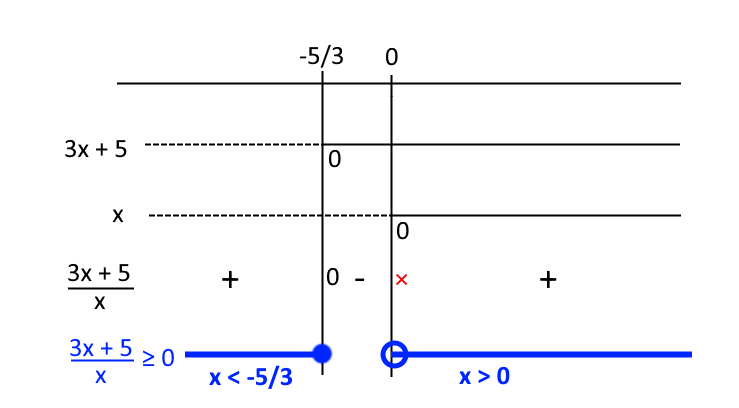
L’insieme delle soluzioni della disequazione è dato dai valori della {x} che rendono la frazione algebrica al primo membro della disequazione in forma normale positiva, compreso inoltre il valore {x=-\dfrac{5}{3}} che annulla il numeratore. Infatti, nella disequazione è presente un simbolo di “maggiore o uguale“, che effettivamente ammette anche l’uguaglianza tra i membri.

Abbiamo invece dovuto escludere il valore {x=0} poiché per esso si annulla il denominatore della frazione.

Così in conclusione la disequazione è verificata per:

x \leq  -\dfrac{5}{3} \quad \vee \quad x > 0

Disequazioni fratte con polinomi anche di grado superiore al primo

Consideriamo ora disequazioni fratte nella forma più generale, ovvero sempre del tipo:

\dfrac{N(x)}{D(x)} \lesseqgtr 0 

ma con {N(x)} e/o {D(x)} di grado superiore al primo. In questa lezione considereremo polinomi comunque scomponibili nel prodotto di polinomi tutti di primo grado.

Esempio 5

Risolvere la seguente disequazione:

\dfrac{x^2-3x+2}{3x-4} \leq 0 

La disequazione è già in forma normale. Scomponendo in fattori il polinomio {N(x)} (numeratore della frazione algebrica al primo membro) otteniamo:

\dfrac{(x-1)(x-2)}{3x-4} \leq 0 

Come al solito si tratterà di studiare il segno della frazione {\dfrac{N(x)}{D(x)}}, individuando di conseguenza l’insieme delle soluzioni della disequazione. In questo caso il numeratore è dato dal prodotto tra due polinomi di primo grado. Basterà quindi ragionare come nel caso delle disequazioni prodotto.

Cominciamo allora studiando il segno del numeratore. Per quanto visto a suo tempo, occorre studiare il segno dei fattori che ne rappresentano la scomposizione in un unico diagramma, per poi applicare le regole dell’algebra dei segni:

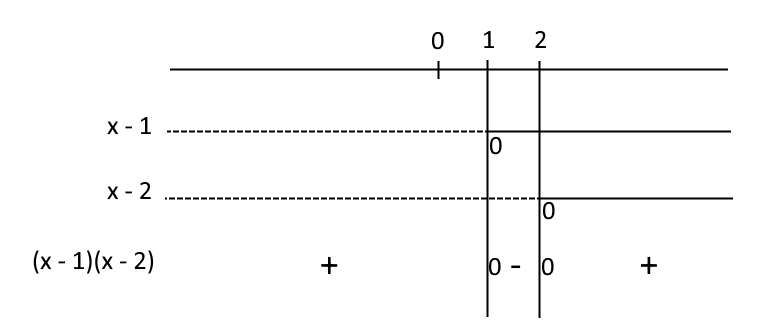
Ora, per poter studiare il segno della frazione \dfrac{N(x)}{D(x)} ci manca ancora lo studio del segno del denominatore:

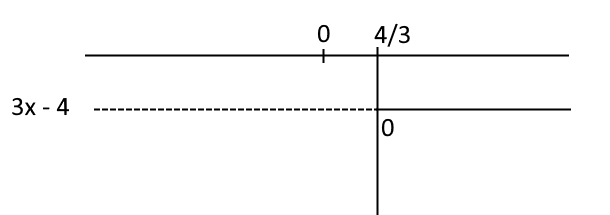
Ora non resta che rappresentare gli studi del segno del numeratore e del denominatore della frazione {\dfrac{N(x)}{D(x)}} in uno stesso diagramma, in modo da individuare l’insieme delle soluzioni della disequazione data grazie all’algebra dei segni (es., meno diviso meno dà più, ecc.):

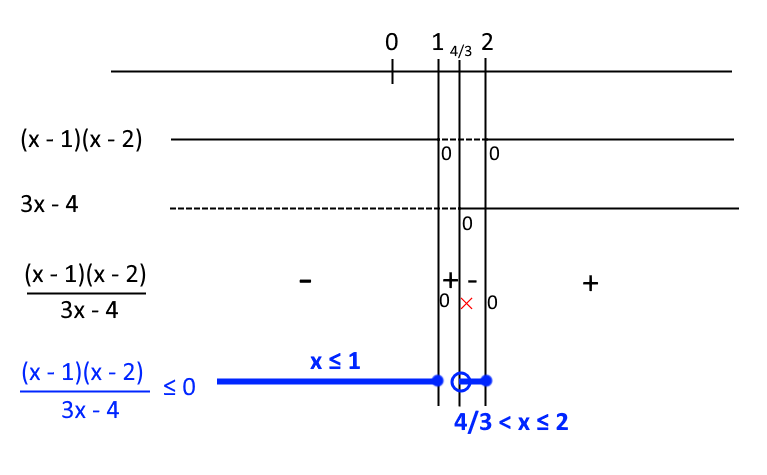
Abbiamo così per la disequazione di partenza l’insieme delle soluzioni dato da:

x  \leq 1 \quad \vee \quad  \dfrac{4}{3}< x \leq 2

Nota. Dato che le regole dell’algebra dei segni sono le stesse sia per la moltiplicazione, sia per la divisione, è possibile raggruppare in un unico diagramma gli studi del segno di tutti i fattori di primo grado che si trovano al numeratore e al denominatore della frazione {\dfrac{N(x)}{D(x)}}. In tal modo è possibile studiare in modo più immediato il segno della frazione stessa (vedi esempio a seguire).

Esempio 6

Vediamo come risolvere le disequazioni fratte nel caso di numeratore e denominatore della frazione {\dfrac{N(x)}{D(x)}} entrambi di grado superiore al secondo.

Risolvere la seguente disequazione fratta:

\dfrac{(2x+5)(2x-1)}{(x+2)(x+1)} < 0

La disequazione si presenta già nella forma normale {\dfrac{N(x)}{D(x)}}, ed in più numeratore e denominatore risultano già scomposti nel prodotto di polinomi di primo grado.

Procediamo studiando direttamente i segni di tutti i fattori presenti a numeratore e a denominatore della frazione a primo membro in un unico diagramma. In tal modo sarà possibile individuare immediatamente l’insieme delle soluzioni della disequazione assegnata. Abbiamo:

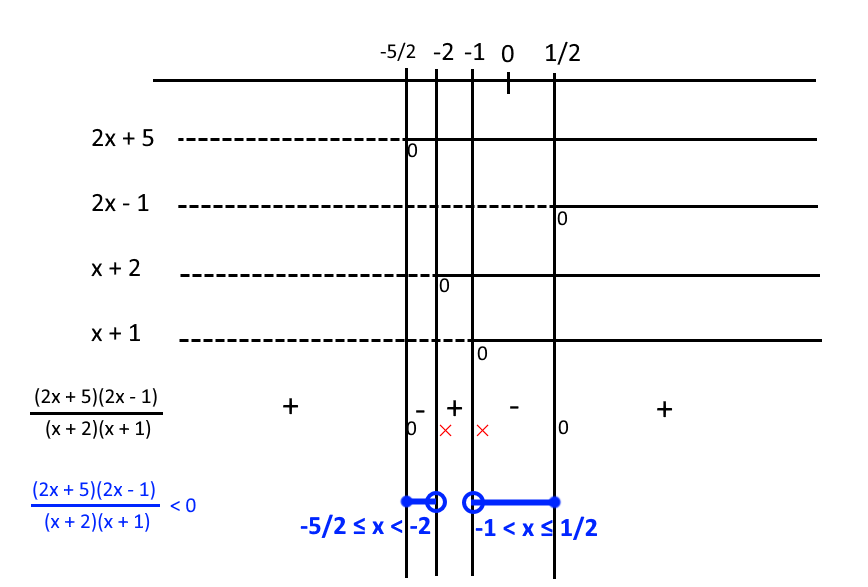
In pratica abbiamo applicato l’algebra dei segni a tutti i fattori a numeratore e denominatore, per ciascun intervallo. Ad esempio, per il primo intervallo abbiamo: meno per meno per meno per meno, che dà più.

In maniera più rapida, basta osservare che se in un intervallo abbiamo un numero dispari di segni meno, allora per la frazione in quell’intervallo avremo segno meno. Se invece il numero di segni meno è pari, per la frazione in quell’intervallo avremo segno più. Infine, come ovvio, se ciascun fattore nell’intervallo risulta positivo, evidentemente anche la frazione sarà in quell’intervallo positiva.

E’ immediato verificare la validità della regola appena enunciata per ciascun intervallo rappresentato nel diagramma. Essa permette di individuare più rapidamente il segno della frazione {\dfrac{N(x)}{D(x)}} in ciascun intervallo, riducendo la possibilità di errore.

Così in conclusione per la disequazione di partenza abbiamo un insieme delle soluzioni individuato dalle condizioni:

 - \dfrac{5}{2} \leq  x < -2 \quad \vee \quad -1 < x \leq \dfrac{1}{2}

Conclusioni

Per quanto riguarda le disequazioni fratte per il momento è tutto. Una volta studiate le disequazioni di secondo grado, vedremo come risolverle in modo ancora più rapido studiando direttamente i segni dei fattori di secondo grado.

Un saluto a tutti e buon proseguimento con SìMatematica!