Le disequazioni lineari in due incognite in forma normale sono date da un polinomio di primo grado nelle due variabili x e y che viene richiesto maggiore, minore, maggiore o uguale oppure minore o uguale a zero. Inoltre, almeno uno dei coefficienti dei termini in x e y deve essere diverso da zero.
Introduciamo così la definizione relativa alle disequazioni lineari in due incognite (o disequazioni lineari in due variabili). Come vedremo tra un istante, per comprendere questo tipo di disequazioni è fondamentale ricordare l’equazione di una retta nel piano. Infatti, l’espressione al primo membro delle disequazioni lineari in due incognite rappresenta una retta in forma implicita (ovvero con variabile dipendente {y} non esplicitata). E, lavorando nel piano, la retta divide il piano stesso in due semipiani.
Così, risolvere le disequazioni lineari in due incognite significa identificare il semipiano individuato dalla particolare disequazione lineare in due incognite che stiamo esaminando.
Disequazioni lineari in due incognite: definizione
Una disequazione lineare in due incognite si presenta nella forma normale:
ax+by+c \lesseqgtr 0
ove con il simbolo {\lesseqgtr} indichiamo un qualunque simbolo di disuguaglianza. I coefficienti {a, \: b, \: c} sono dei numeri reali, ed i due coefficienti {a, \: b} non possono essere entrambi nulli.
Al primo membro della disequazione abbiamo un polinomio di primo grado nelle due variabili {x} e {y}. Poiché l’esponente che accompagna ciascuna lettera non è mai maggiore di {1}, la disequazione è lineare.
Ora, l’espressione al primo membro rappresenta una retta in forma implicita:
ax+by+c=0 \qquad \text{retta}Se infatti esplicitiamo la {y} (ipotizzando {b \neq 0}) otteniamo:
by=-ax-c \quad \Rightarrow \quad y=-\dfrac{a}{b}x-\dfrac{c}{b}In questo modo ritroviamo l’equazione di una retta nella forma probabilmente più familiare {y=mx+q}, ponendo {m=-\dfrac{a}{b}} e {q=-\dfrac{c}{b}}.
Ora, tale retta divide il piano in due semipiani {\alpha_1} e {\alpha_2}.
Per risolvere le disequazioni lineari in due incognite dobbiamo capire quale dei due semipiani {\alpha_1} e {\alpha_2} è individuato dalla disequazione. Si tratterà quindi di rappresentare graficamente la retta corrispondente all’espressione al primo membro della disequazione data, e quindi evidenziare con una campitura il semipiano individuato dalla disequazione stessa. Tutti i punti di tale semipiano sono soluzioni della disequazione data.
Cominciamo subito con degli esempi.
Esempi sulle disequazioni lineari in due incognite
Esempio 1
Risolvere la disequazione:
3x-y+2<0
Il primo passo per risolvere le disequazioni lineari in due incognite è quello di disegnare la retta rappresentata dall’equazione che si ottiene uguagliando il primo membro della disequazione data a zero.
Cominciamo quindi disegnando nel piano la retta:
3x-y+2=0
che in forma esplicita diviene:
-y=-2-3x \quad \Rightarrow \quad y=3x+2
Il coefficiente angolare è {m=3} (il coefficiente del termine in {x}) mentre il termine noto o ordinata all’origine è {2}. Così, abbiamo che il punto {P_1=(0,2)} appartiene alla retta.
Per poter disegnare la retta, ci serve un altro punto appartenete ad essa. Valutiamo ad esempio la funzione {y=3x+2} per {x=1}. Otteniamo:
y=3x+2=3\cdot1+2=5
Così {P_2=(1,5)} è un altro punto appartenente alla retta. Possiamo così disegnare la retta {y=3x+2} come segue:
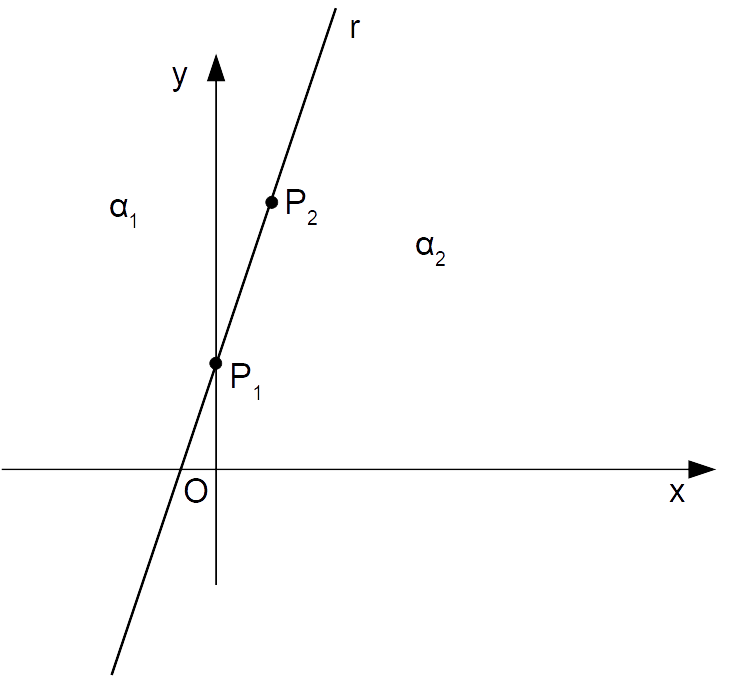
Ora, per determinare le soluzioni delle disequazioni lineari di due equazioni in due incognite, si tratta di capire quale semipiano viene individuato dalla disequazione di partenza:
3x-y+2<0
Per fare questo, basta sostituire nel primo membro della disequazione le coordinate di un punto appartenente ad {\alpha_1} oppure ad {\alpha_2}, a nostra scelta. Sostituiamo ad esempio il punto {P_3=(0,4)}, che appartiene ad {\alpha_2}:
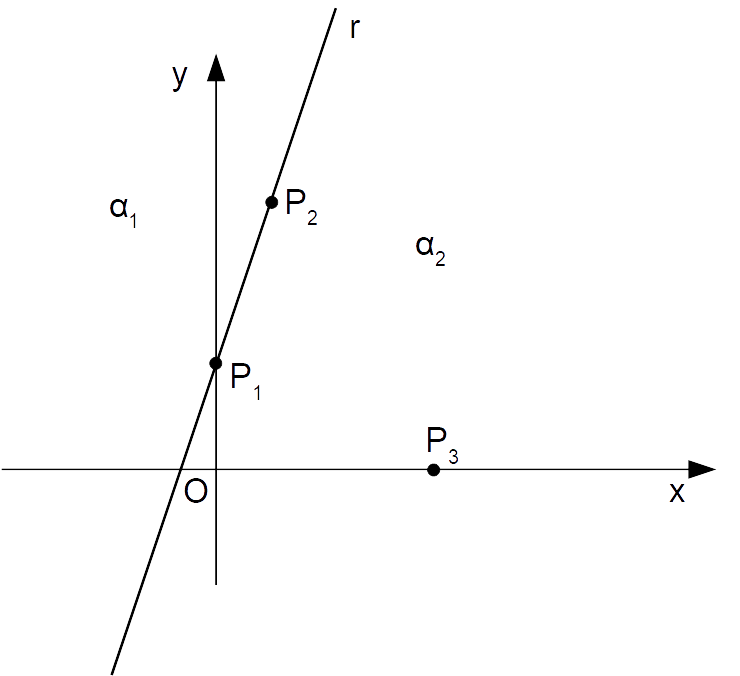
Sostituendo {x=4} e {y=0} nella disequazione di partenza otteniamo una disuguaglianza numerica:
3x-y+2<0 \quad \Rightarrow \quad 3 \cdot 4 - 0+2 < 0 \quad \Rightarrow \quad 14<0
La disuguaglianza è evidentemente falsa. Ciò significa che la disequazione data non è verificata in corrispondenza di un punto appartenente al semipiano {\alpha_2}. Di conseguenza, la disequazione rappresenta il semipiano {\alpha_1}:
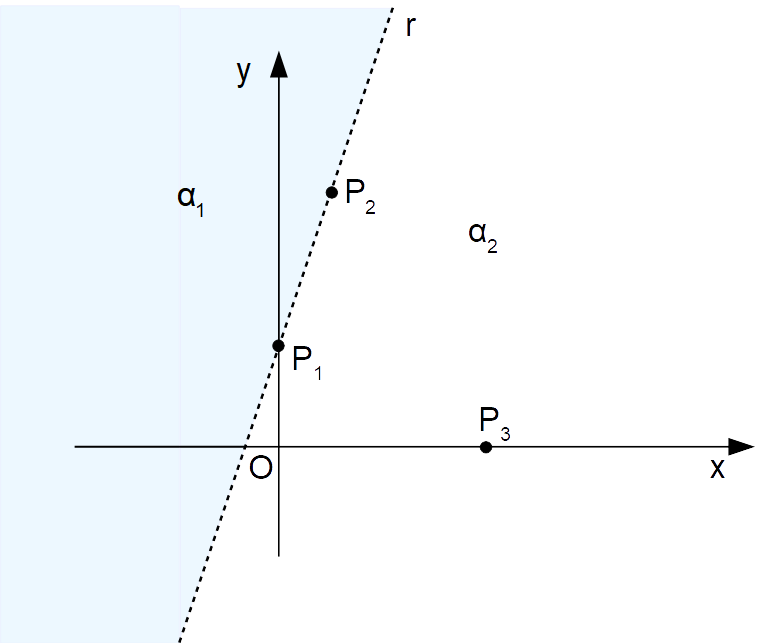
Abbiamo evidenziato il semipiano rappresentato dalla disequazione colorandolo. E per indicare che la disequazione data rappresenta il semipiano {\alpha_1} scriviamo:
\alpha_1 : 3x-y+2 < 0
E’ infine importante rilevare che abbiamo rappresentato la retta che individua i due semipiani con stile tratteggiato. Ciò è dovuto al fatto che nella disequazione di partenza abbiamo il simbolo di disuguaglianza “minore” e non “minore o uguale”. Di conseguenza i punti della retta non appartengono ad {\alpha_1} poiché la disequazione esclude l’uguaglianza tra i due membri. E dunque le coordinate di tutti i punti della retta, che effettivamente annullano il primo membro, non soddisfano la disequazione.
Per scrupolo, anche se non necessario, possiamo considerare un punto del semipiano {\alpha_1} e vedere se effettivamente soddisfa la disequazione di partenza. Prendiamo ad esempio {P_4=(0,3)}:
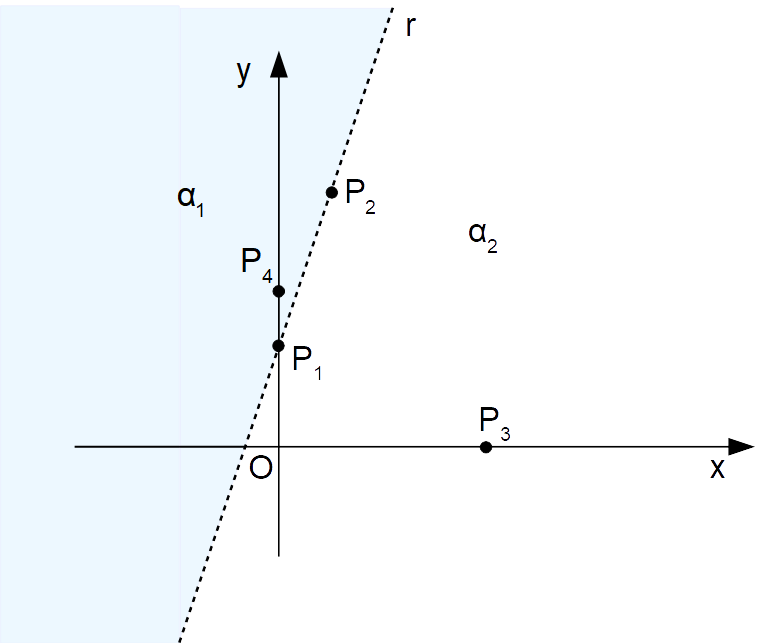
Abbiamo:
3x-y+2 < 0 \quad \Rightarrow \quad 3 \cdot 0-3+2 < 0 \quad \Rightarrow \quad -1<0
Otteniamo in questo modo una disequazione numerica vera, e quindi ciò conferma che la disequazione {3x-y+2 < 0} effettivamente rappresenta il semipiano {\alpha_1}.
Così in conclusione tutte le coppie {(x, \: y)} relative ai punti del semipiano {\alpha_1} sono soluzioni della disequazione di partenza.
Esempio 2
Risolvere la seguente disequazione lineare in due incognite:
3x-7y+5\geq 0
Cominciamo tracciando la retta di equazione:
3x-7y+5=0
Esplicitiamo la {y}:
-7y=-3x-5 \quad \Rightarrow \quad y=\dfrac{3x+5}{7} \quad \Rightarrow \quad y=\dfrac{3}{7}x+\dfrac{5}{7}Si tratta così della retta con ordinata all’origine {q=\dfrac{5}{7}}. Di conseguenza il punto {P_1=(0,5/7)} appartiene alla retta. Determiniamo un altro punto ad esempio a partire dall’ascissa {x=1}. Otteniamo l’ordinata:
y=\dfrac{3}{7}\cdot1+\dfrac{5}{7}=\dfrac{8}{7}Così anche il punto {P_2=(1, 8/7)} appartiene alla retta, che possiamo così tracciare (disegno qualitativo):
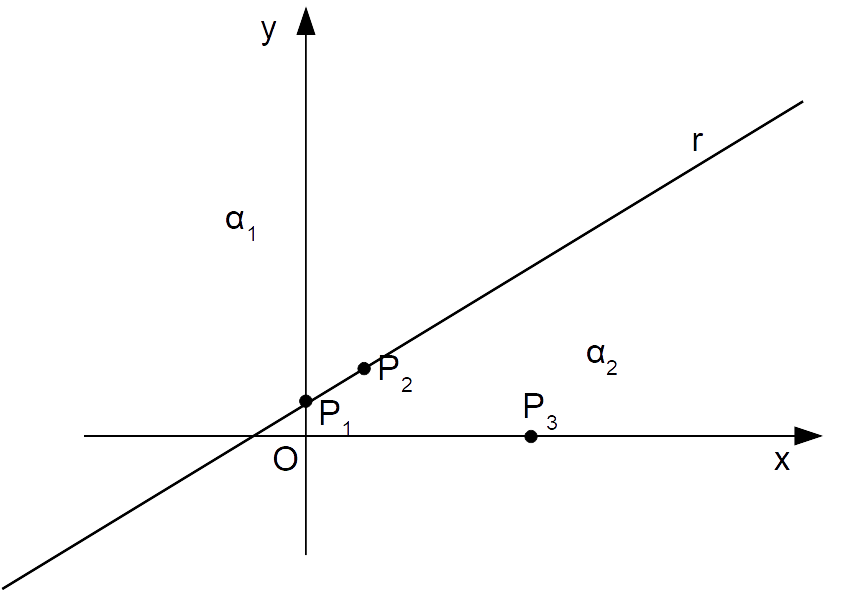
Ora, per individuare quale semipiano rappresenta la disequazione data, consideriamo il punto {P_3=(4,0)} in figura del semipiano {\alpha_2}, sostituiamo le sue coordinate nella disequazione e vediamo se otteniamo una disuguaglianza numerica vera o falsa.
\begin{align*} & 3x-7y+5\geq 0 \quad \text{con} \quad x=4, \: y=0\\ \\ &\Rightarrow 3 \cdot 4 - 7 \cdot 0 +5 \geq 0 \quad \Rightarrow \quad 17 \geq 0\end{align*}La disuguaglianza numerica ottenuta è vera. Di conseguenza, il punto {P_3} soddisfa la disequazione, la quale pertanto rappresenta il semipiano {\alpha_2}:
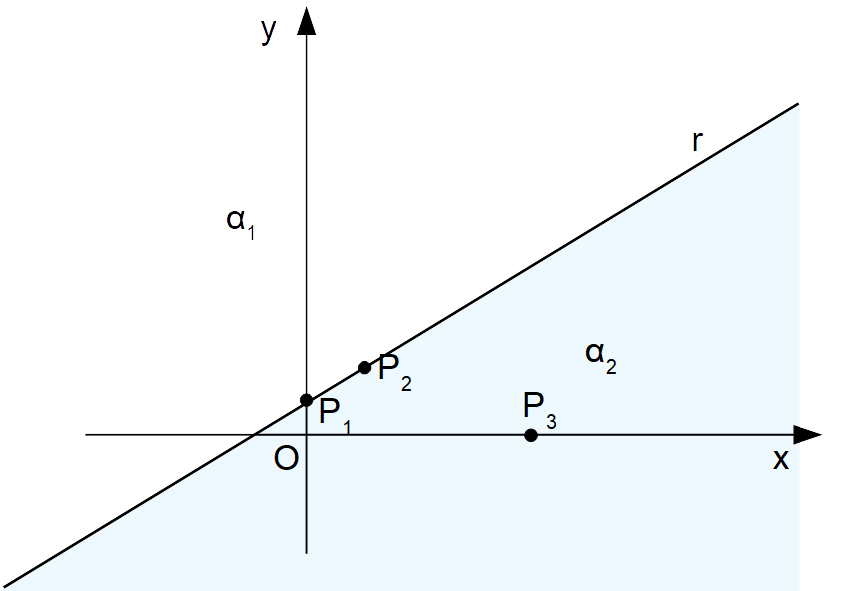
In conclusione tutti i punti del semipiano {\alpha_2} sono soluzioni della disequazione di partenza. Osserviamo che la retta è disegnata con tratto continuo poiché anche i suoi punti fanno parte delle soluzioni della disequazione. Infatti, nella disequazione stessa compare il simbolo di “maggiore o uguale” e non di “maggiore”. Per cui è permessa anche l’uguaglianza tra i due membri.
Disequazioni lineari di una incognita nel piano
E’ anche possibile risolvere nel piano disequazioni lineari che presentano una sola incognita. Si tratta di disequazioni sempre della forma generale:
ax+by+c \lesseqgtr 0
nelle quali però risulti {a=0} oppure {b=0}.
Ad esempio, disequazioni del tipo:
ax+c \lesseqgtr 0, \qquad a, \: c \in \R
avranno per soluzioni le coordinate di tutti i punti di uno dei due semipiani delimitati dalla retta verticale {x=-\dfrac{c}{a}}. Allo stesso modo, disequazioni della forma:
by +c\lesseqgtr 0, \qquad b, \: c \in \R
avranno per soluzioni le coordinate di tutti i punti di uno dei due semipiani delimitati dalla retta orizzontale {y=-\dfrac{c}{b}}.
Esempio 3
Risolvere nel piano la disequazione:
2x-5 > 0
Cominciamo tracciando la retta:
2x-5 = 0
ovvero in forma esplicita:
2x=5 \quad \Rightarrow \quad x=\dfrac{5}{2}
La retta individua due semipiani {\alpha_1} e {\alpha_2}. Ora, riscriviamo la disequazione di partenza:
2x-5 > 0
come:
x > \dfrac{5}{2}Le soluzioni dell’equazione sono date da tutti i punti tali da avere ascissa maggiore di {\dfrac{5}{2}}. Quindi il semipiano {\alpha_2} è soluzione della disequazione:
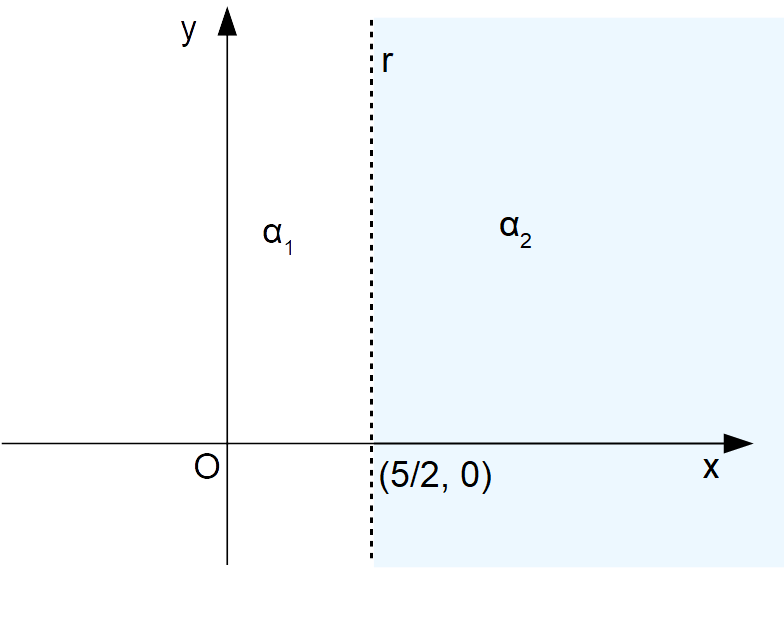
Osserviamo che abbiamo disegnato la retta {x=\dfrac{5}{2}} con stile tratteggiato poiché i suoi punti non sono soluzioni della disequazione di partenza. Ciò ancora una volta è dovuto al particolare simbolo di disuguaglianza presente, tale da escludere l’uguaglianza.
Esempio 4
Risolvere la disequazione:
5y-10 \leq 0
Cominciamo disegnando la retta:
5y-10 = 0
ovvero:
y=\dfrac{10}{5}; \qquad \Rightarrow \quad y=2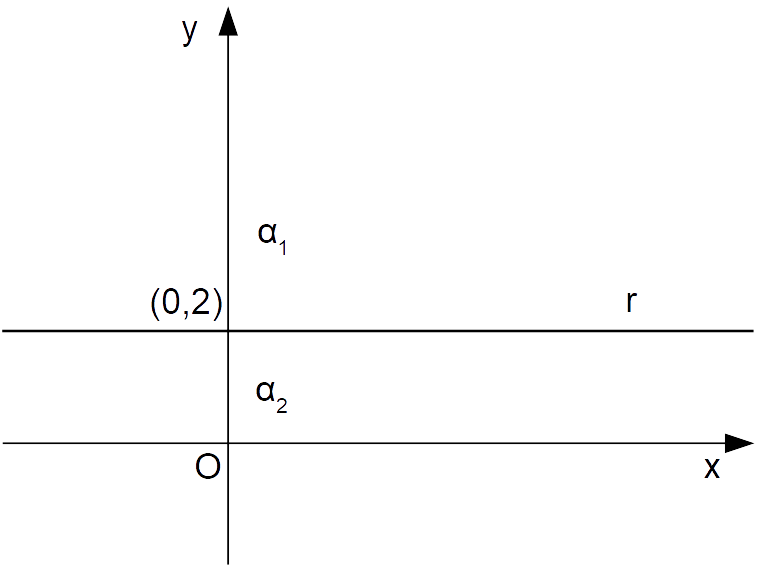
Ora riscriviamo la disequazione di partenza:
5y-10 \leq 0
come:
y \leq 2
Le soluzioni della disequazione sono date dalle coordinate di tutti i punti aventi ordinata minore o uguale a {2}:
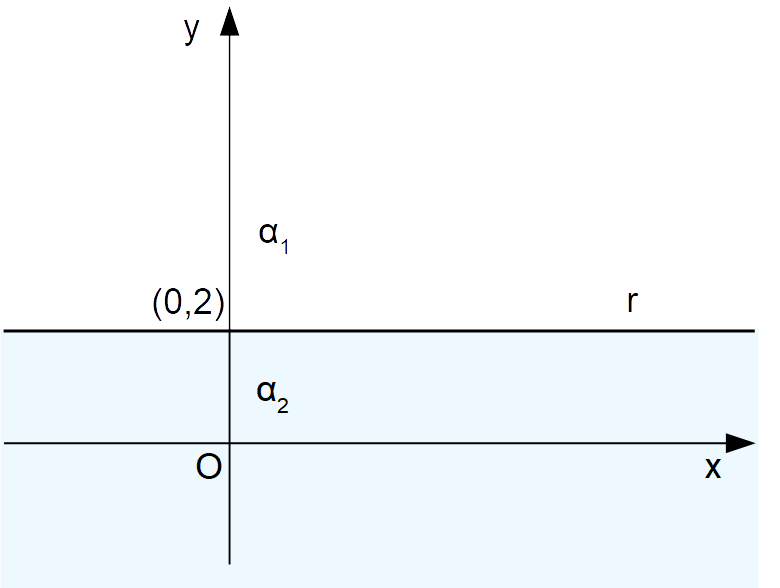
Dato che il simbolo di uguaglianza comprende l’uguale, anche i punti della retta {y=2} sono soluzioni della disequazione.
Conclusioni
Per quanto riguarda questa lezione sulle disequazioni lineari in due incognite è tutto. E per le considerazioni sin qui fatte possiamo concludere che è possibile rappresentare un semipiano (che è un dominio piano, ovvero una particolare regione di piano) utilizzando delle disequazioni lineari in due incognite.
A partire dalla prossima lezione ci occuperemo dei domini piani delimitati da rette: angolo, striscia e poligono. In altre parole, individueremo delle regioni di piano particolari utilizzando delle rette. Buon proseguimento!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
