Divisione tra polinomi

 - 

Monomi e polinomi (superiori)

Ci occupiamo ora dell’ultima operazione tra polinomi: la divisione tra polinomi. Tale operazione si esegue con una regola molto simile alla divisione tra numeri così come la conosciamo dall’aritmetica. Abbiamo visto nella scorsa lezione la divisione di un polinomio per un monomio. Tuttavia, la divisione tra polinomi segue una procedura nettamente diversa. E’ comunque necessario anche in questo caso conoscere la divisione tra monomi.

Precisiamo anzitutto che è possibile eseguire la divisione tra due polinomi qualsiasi, così come è possibile dividere tra loro due numeri qualsiasi (purché, ovviamente, il numero o polinomio divisore sia non nullo). Infatti, nell’operazione di divisione tra polinomi otteniamo un quoziente e un eventuale resto che appartengono sempre all’insieme dei polinomi. Di conseguenza, posta l’unica condizione che il divisore sia diverso da zero, l’operazione è sempre possibile e risulta interna all’insieme dei polinomi.

Ora, per caratterizzare la divisione tra polinomi occorre anzitutto stabilire un criterio di divisibilità tra polinomi, ovvero sapere quando un polinomio {D(x)} risulta divisore di un polinomio {P(x)}. Inoltre, ci servirà anche un teorema in grado di assicurarci l’esistenza e l’unicità del quoziente {Q(x)} e dell’eventuale resto {R(x)} della divisione.

Osserviamo comunque fin da subito che per eseguire la divisione tra polinomi non è necessario che i polinomi siano tra loro divisibili. Questa è un’importante differenza rispetto alla divisione di un polinomio per un monomio, la quale invece richiede necessariamente la divisibilità. Così, se i due polinomi sono divisibili il risultato della loro divisione sarà dato da un quoziente completo (e quindi resto zero). Diversamente, otterremo come risultato un certo quoziente ed un resto necessariamente non nullo.

Infine, nel caso particolare in cui il grado del polinomio divisore sia maggiore del grado del polinomio dividendo, la divisione è comunque possibile ma otterremo come risultato un quoziente nullo e resto pari al polinomio dividendo. In questa circostanza è dunque possibile eseguire immediatamente la divisione senza alcun calcolo. E osserviamo che siamo ancora nel caso di polinomi non divisibili tra loro (infatti, il resto è diverso da zero).

Fatte le dovute premesse, vediamo subito i concetti teorici e la regola pratica riguardanti la divisione tra polinomi.

Teoria e regola pratica per la divisione tra polinomi

Dati due polinomi {P(x)} e {D(x)}, con {D(x) \neq 0}, consideriamo la divisione tra polinomi:

P(x):D(x)

Il polinomio {P(x)} è divisibile per il polinomio {D(x)} se esiste un polinomio {Q(x)} tale che: {Q(x) \cdot D(x) = P(x)}

In tal caso {Q(x)} rappresenta il quoziente esatto della divisione ed abbiamo:

\dfrac{P(x)}{D(x)}=Q(x)

Se invece il polinomio {P(x)} non è divisibile per il polinomio {Q(x)} è comunque possibile eseguire la divisione ma la precedente relazione non potrà essere soddisfatta.

Vale però il seguente teorema.

Teorema. Se {P(x)} è un polinomio di grado {n} e {D(x) \neq 0} è un polinomio di grado {m}, con {n \geq m}, allora esistono due polinomi {Q(x)} e {R(x)} tali che risulti: {Q(x) \cdot D(x)+R(x) = P(x)} con grado del resto {R(x)} minore del grado {m} del divisore.

Se invece il grado del polinomio divisore {D(x)} è maggiore del grado del polinomio dividendo {P(x)}, il grado del resto non risulterà minore del grado del polinomio divisore ed in particolare la divisione {P(x):D(x)} fornirà quoziente {Q(x)=0} e resto {R(x)=P(x)}.

Consideriamo degli esempi, per ora dando per buoni i quozienti e i resti che otterremo.

La divisione:

(x^2-2x+1):(x-1)

restituisce quoziente {x-1} e resto zero. Ciò significa che il polinomio {x^2-2x+1} è divisibile per il polinomio {x-1}. Infatti, se moltiplichiamo il quoziente per il divisore otteniamo il dividendo:

Q(x)\cdot D(x) = (x-1) \cdot (x-1)=x^2-2x+1=P(x)

Invece, la divisione:

(2x^3+3x^2-5x+7):(x^2+3x-9)

fornisce quoziente {Q(x) = 2x-3} e resto {R(x)=22x-20}. Il resto è diverso da zero e quindi il polinomio {2x^3+3x^2-5x+7} non è divisibile per il polinomio {x^2+3x-9}. Inoltre, poiché il grado del polinomio dividendo è non inferiore al grado del polinomio divisore, abbiamo ottenuto un quoziente non nullo.

Infine, considerando la divisione:

(x^2+2x):(x^3+9x+7)

poiché il grado del polinomio divisore è maggiore del grado del polinomio dividendo, otteniamo senza alcun calcolo quoziente {Q(x)=0} e resto {R(x)=x^2+2x}. Il resto è quindi nel caso in esame uguale al dividendo ed è di grado non inferiore ma bensì uguale a quello del dividendo.

Regola per il calcolo della divisione tra polinomi

Nel caso in cui il grado del polinomio dividendo {P(x)} sia maggiore o uguale al grado del polinomio divisore {Q(x)} il calcolo della divisione tra polinomi {P(x):Q(x)} consiste nel determinare il quoziente {Q(x)} (necessariamente diverso da zero) e il resto (che potrà invece essere diverso da zero ma anche nullo). Se il resto che calcoleremo sarà nullo diremo che il polinomio {P(x)} è divisibile per il polinomio {D(x)}.

Per il calcolo della divisione tra polinomi sono necessarie le seguenti operazioni:

• divisione tra monomi;
• moltiplicazione di un monomio per un polinomio;
• somma algebrica tra polinomi.

In particolare si tratterà di calcolare uno o più resti parziali, fintanto che il grado del resto parziale ottenuto non risulterà minore del grado del polinomio divisore. In altre parole, capiremo che il resto parziale ottenuto coinciderà con il resto finale {R(x)} della divisione quando questo avrà grado minore del grado del divisore. E ciò è in accordo con quanto richiesto dal precedente teorema sull’esistenza del quoziente e del resto. Verificata quindi tale condizione, l’operazione di divisione tra polinomi sarà terminata.

Vediamo in pratica la regola da seguire con un esempio, relativo al caso di polinomi con una sola lettera. Calcoliamo la divisione:

(16-25a^2):(-4+5a)

Anzitutto occorre ordinare entrambi i polinomi per potenze decrescenti rispetto alla lettera presente. Così dobbiamo riscrivere la divisione come:

(-25a^2+16):(5a-4)

Inoltre, occorre sempre scrivere il polinomio dividendo in forma completa. Nel nostro caso manca il termine in {a} per cui scriveremo:

(-25a^2+0a+16):(5a-4)

Come nel caso della divisione tra numeri, costruiamo la seguente tabella:

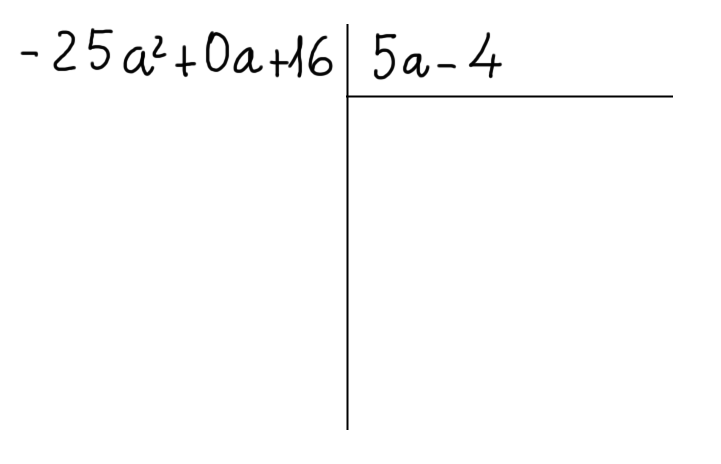
Cominciamo evidenziando con un “cappello” il primo termine del dividendo e il primo termine del divisore:

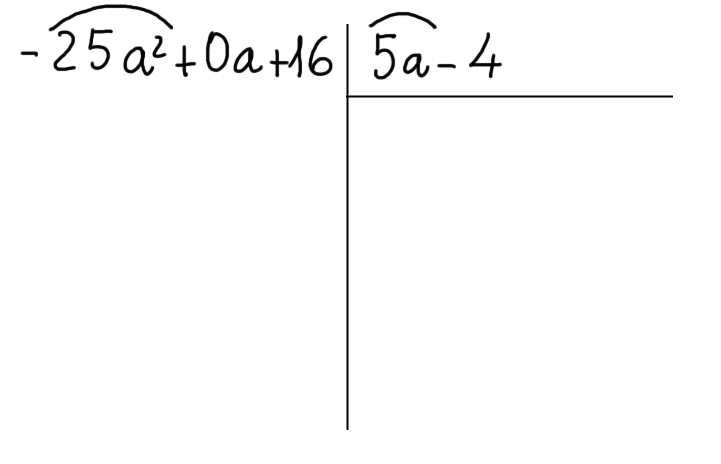
A questo punto dividiamo il primo termine del dividendo per il primo termine del divisore (dividiamo tra loro i due termini evidenziati). Scriviamo il risultato sotto al divisore:

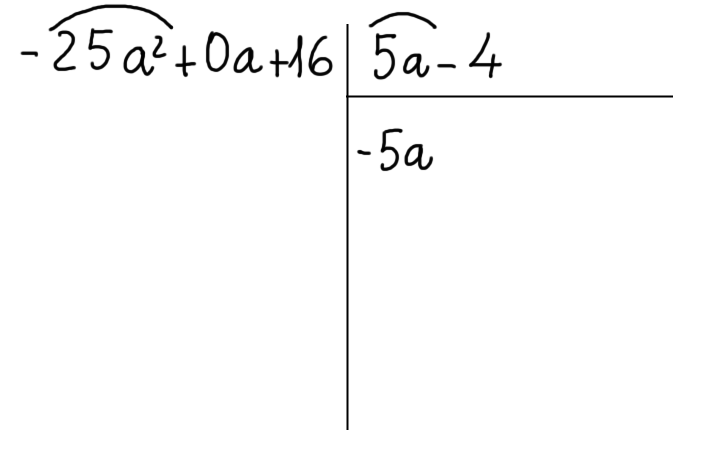
Questo è il primo termine del quoziente.

Ora moltiplichiamo il monomio appena scritto per il primo termine del divisore. Otteniamo il monomio {-25a^2}. Cambiamo il segno del monomio ottenuto e scriviamolo al di sotto del termine del dividendo che ha il suo stesso grado. Questo è il primo termine del quoziente:

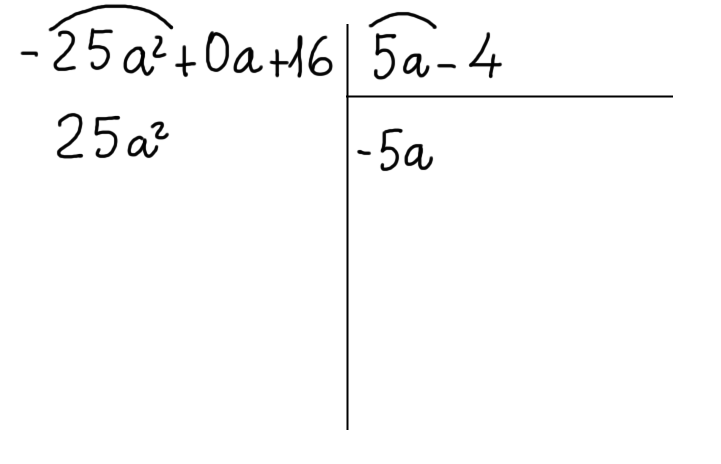
Ora moltiplichiamo il primo termine del quoziente per il secondo termine del divisore. Scriviamo il risultato invertito di segno sotto il termine del dividendo che ha il suo stesso grado:

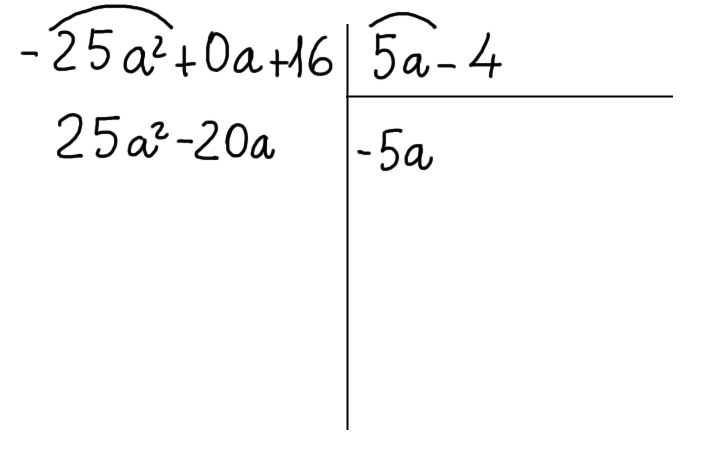
Ora tiriamo una riga sotto gli ultimi termini scritti ed eseguiamo la somma algebrica tra ciascun termine del dividendo ed i termini simili ad esso sottostanti:

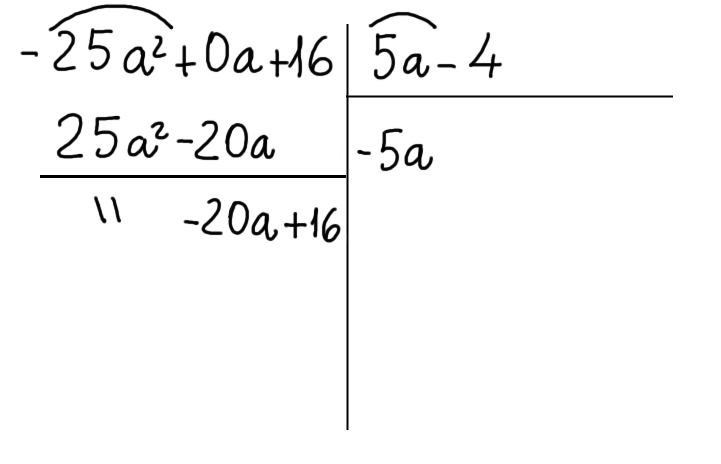
Osserviamo che poiché non c’è nessun termine sotto il {16} ci limitiamo semplicemente a riscriverlo. Abbiamo così scritto il primo resto parziale. Poiché il suo grado non è inferiore a quello del polinomio divisore, dobbiamo continuare con l’operazione.

Procediamo evidenziando il primo termine del resto parziale:

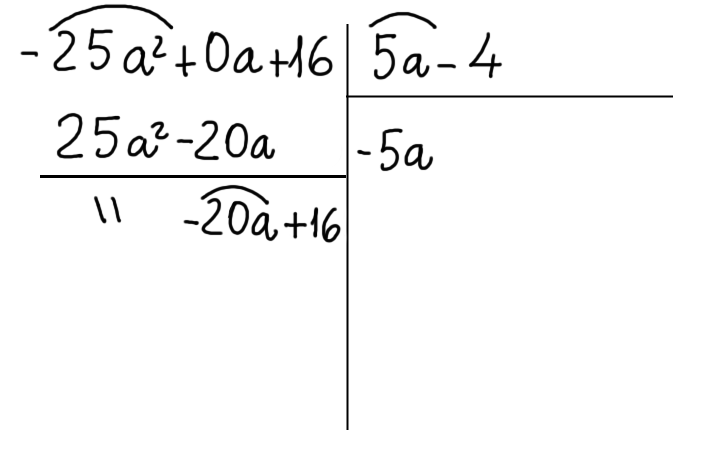
Ora dividiamo il termine evidenziato per il primo termine del polinomio divisore. Scriviamo il risultato a fianco del primo termine del quoziente. Questo sarà il secondo termine del quoziente.

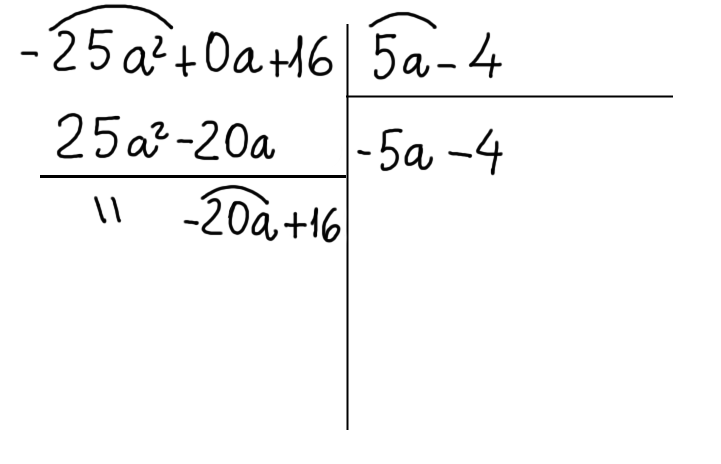
Ora moltiplichiamo il secondo termine del quoziente per il primo termine del polinomio divisore. Invertiamo il segno del risultato ottenuto e scriviamolo al di sotto del termine di uguale grado nel primo resto parziale:

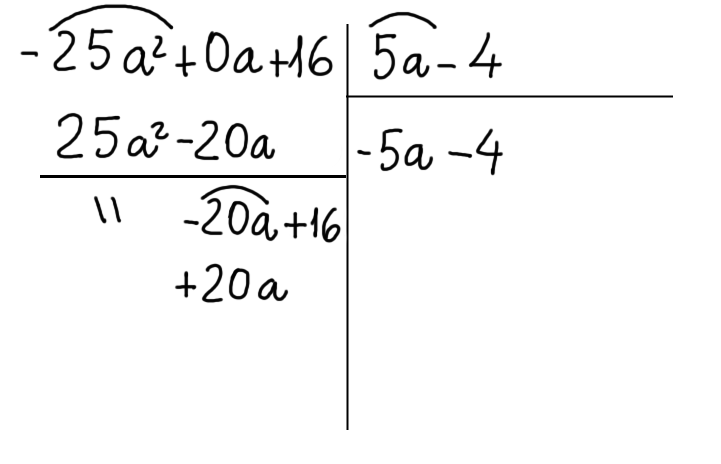
Procediamo moltiplicando sempre il secondo termine del quoziente stavolta per il secondo termine del polinomio divisore. Invertiamo il segno del risultato ottenuto e scriviamolo, di nuovo, al di sotto del termine del resto parziale di uguale grado:

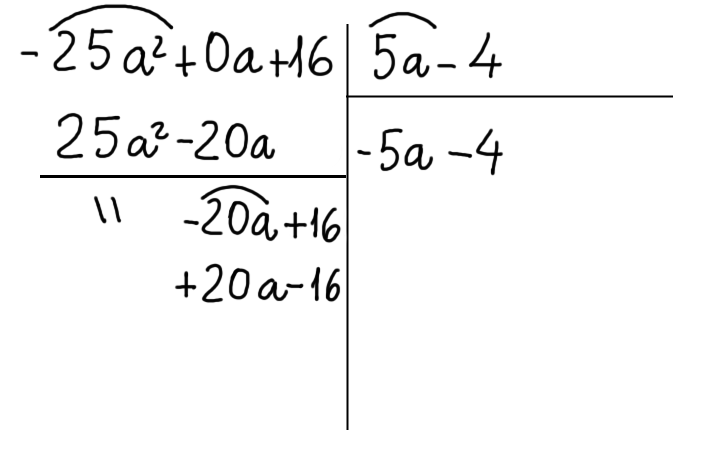
Ora tiriamo una riga al di sotto degli ultimi termini scritti e sommiamo algebricamente ciascun termine del resto parziale con i termini simili sottostanti:

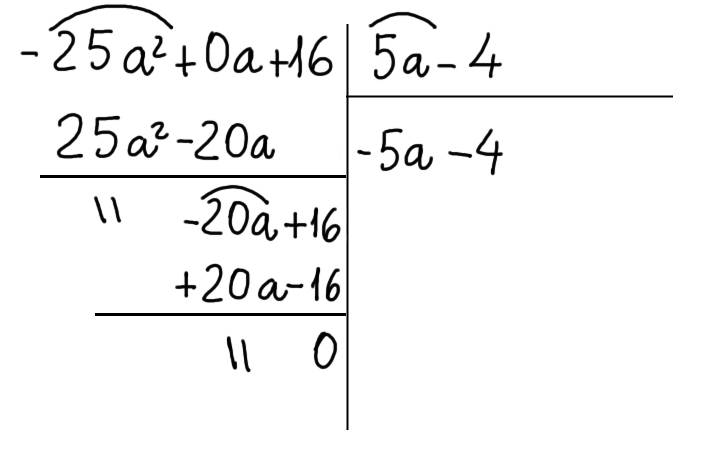
Otteniamo il secondo resto parziale, che in questo caso è zero ed è quindi di grado inferiore rispetto al divisore. La divisione di conseguenza termina qui ed otteniamo in conclusione:

Q(x)=-5a-4; \qquad R(x)=0

Poiché il resto è zero il quoziente ottenuto è esatto. Quindi possiamo affermare che il polinomio {16-25a^2} è divisibile per il polinomio {-4+5a}.

Divisione tra polinomi con più lettere

Nel caso della divisione tra polinomi con più lettere le regole da seguire sono praticamente le stesse della divisione tra polinomi con una sola lettera, a patto di dover scegliere fra le lettere presenti la variabile di riferimento.

Così ad esempio la divisione:

(x^2-ax+a^2):(x+2a)

potrà essere eseguita sia rispetto alla lettera {x}, sia rispetto alla lettera {a}. Ora, se la divisione è esatta (quoziente esatto), in entrambi i casi otteniamo gli stessi quozienti e resto (quoziente uguale e resto zero). Se invece la divisione non è esatta, in ciascun caso otteniamo quoziente e resto differenti. Di conseguenza, è importante stabilire rispetto a quale lettera eseguiamo una divisione tra polinomi con più lettere.

Ora, nell’eseguire la divisione dovremo ordinare entrambi i polinomi rispetto alla lettera scelta, trattando le lettere rimanenti come costanti.

La divisione sarà terminata quando il grado dell’ultimo resto parziale rispetto alla lettera scelta è minore del grado del divisore anch’esso rispetto alla lettera scelta.

Veniamo subito alla pratica. Eseguiamo la seguente divisione prendendo come variabile di riferimento la lettera {x}:

(x^2-ax+a^2):(x+2a)

Osserviamo che entrambi i polinomi sono già ordinati (per potenze decrescenti) rispetto alla lettera {x}. Inoltre, il dividendo è completo rispetto alla lettera {x} e quindi non dobbiamo riscriverlo nella forma “forzatamente completa” (usando coefficienti nulli per i termini mancanti).

Possiamo allora procedere con la divisione, utilizzando le regole utilizzate in precedenza. Dobbiamo soltanto osservare che tutte le lettere diverse dalla lettera scelta per la divisione dovranno essere trattate come numeri. Così in questo caso ad esempio nel monomio {-ax} dovremo considerare come parte letterale {x} e come parte numerica {-a} (quindi un coefficiente parametrico).

Cominciamo scrivendo la tabella:

Evidenziamo il primo termine del dividendo ed il primo termine del divisore:

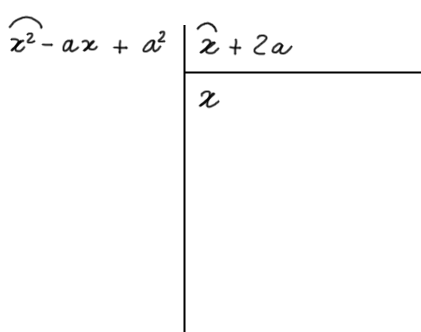
Eseguiamo a questo punto la divisione tra il primo termine del dividendo e il primo termine del divisore:

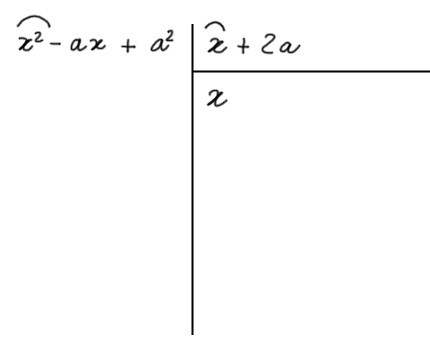
Abbiamo così scritto il primo termine del quoziente. Ora moltiplichiamo tale termine per il primo termine del divisore. Invertiamo il segno del risultato appena ottenuto e scriviamolo sotto il termine del dividendo che ha lo stesso grado rispetto alla lettera {x}:

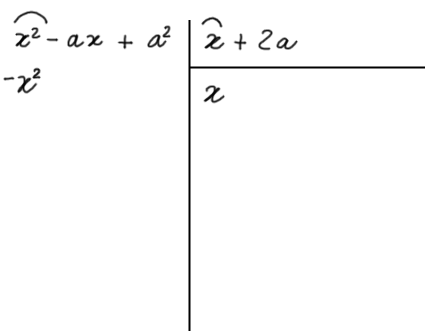
Ora continuiamo moltiplicando il primo termine del quoziente per il secondo termine del divisore. Ancora, invertiamo il segno del risultato ottenuto e scriviamolo sotto al termine del dividendo di uguale grado rispetto alla {x}:

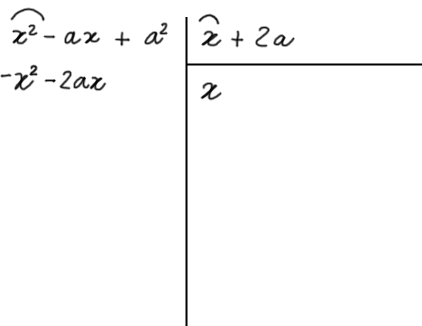
Ora tiriamo una riga sotto gli ultimi termini scritti e sommiamo algebricamente ciascuno dei termini del dividendo con i sottostanti termini simili:

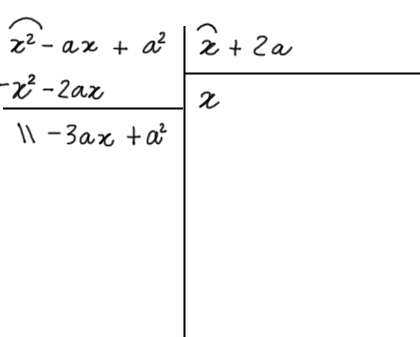
Il termine a^2 viene semplicemente riscritto poiché non c’è nessun termine da sommare ad esso.

Abbiamo così ottenuto il primo resto parziale. Osserviamo che il suo grado rispetto alla {x} è non inferiore al grado rispetto alla {x} del divisore. Di conseguenza dobbiamo continuare. Evidenziamo il primo termine del primo resto parziale:

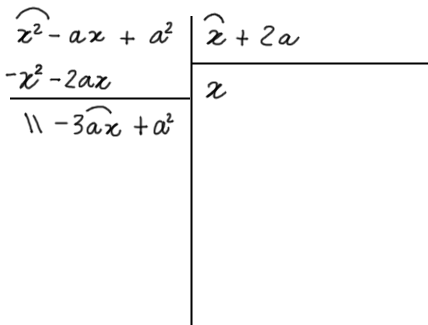
Dividiamo quindi il primo termine del primo resto parziale per il primo termine del divisore. Scriviamo il risultato a fianco del primo termine del quoziente. Abbiamo così il secondo termine del quoziente:

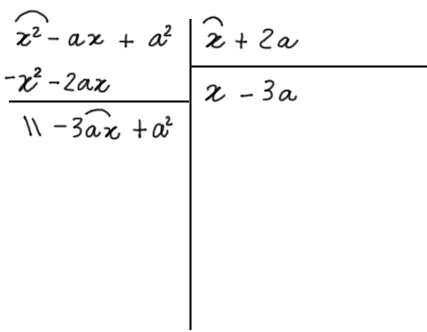
Ora moltiplichiamo il secondo termine del quoziente per il primo termine del divisore. Invertiamo il segno del risultato ottenuto e scriviamolo sotto il termine dello stesso grado in {x} nel primo resto parziale:

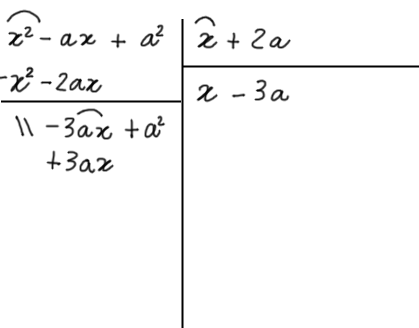
In maniera simile, moltiplichiamo il secondo termine del quoziente per il secondo termine del divisore. Invertiamo il segno del risultato ottenuto e scriviamolo sotto il termine del resto parziale dello stesso grado rispetto alla {x} (in questo caso, grado zero poiché la lettera {x} non figura nei termini considerati).

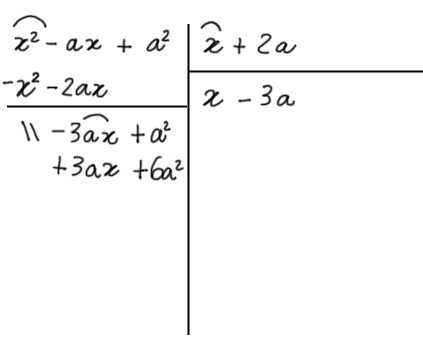
Ora, tracciamo una linea sotto gli ultimi termini scritti e sommiamo algebricamente i termini simili in colonna, come fatto in precedenza:

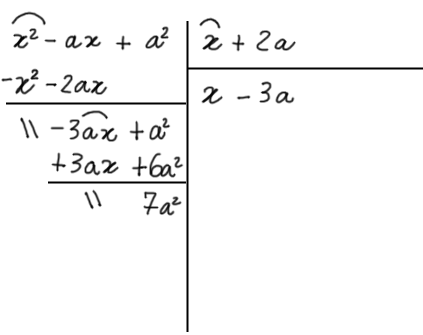
Poiché il grado del resto parziale ottenuto rispetto ad {x} è inferiore rispetto al grado del divisore sempre rispetto ad {x}, la divisione è terminata. Abbiamo ottenuto:

Q(x)=x-3a; \qquad R(x)=7a^2

Ora, rifacciamo la stessa divisione ma consideriamo come variabile di riferimento la lettera {a}. Riprendiamo la divisione di partenza:

(x^2-ax+a^2):(x+2a)

Attenzione: stavolta la {x} va considerata come un numero e dobbiamo ordinare i polinomi rispetto alla lettera {a}. Così abbiamo:

(a^2-ax+x^2):(2a+x)

Osserviamo che il dividendo è completo rispetto alla lettera {a} per cui non dobbiamo effettuare alcun aggiustamento per renderlo “completo”.

Scriviamo la tabella:

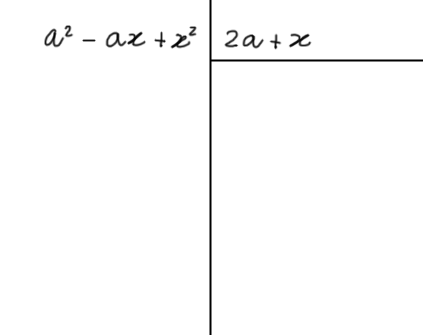
Calcoliamo il primo termine del quoziente come nei casi precedenti:

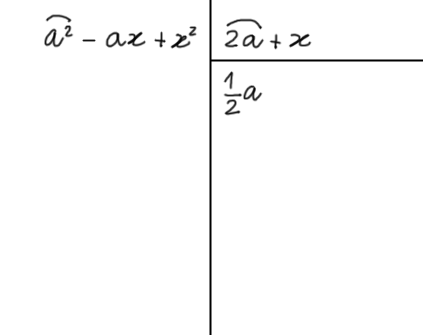
Moltiplichiamo il primo termine del quoziente per il primo termine del divisore, invertiamo il segno del risultato ottenuto e scriviamolo sotto il termine dello stesso grado rispetto alla {a} del polinomio dividendo:

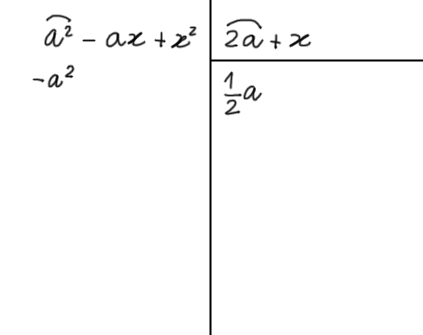
Procedendo in modo simile lavorando però con il secondo termine del polinomio divisore:

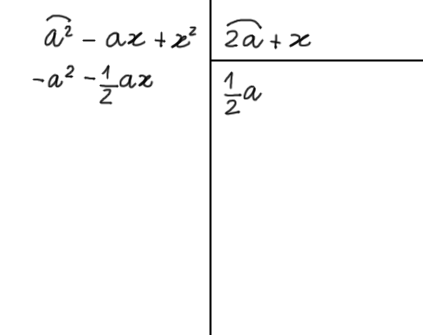
A questo punto sommiamo algebricamente i termini in colonna:

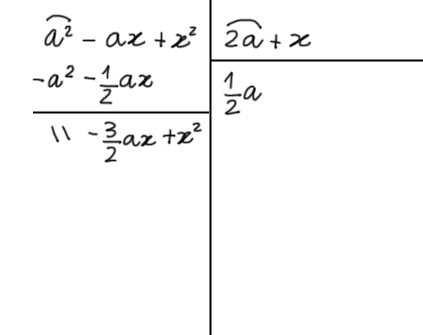
Ora dividiamo il primo termine del primo resto parziale con il primo termine del divisore. Eseguiamo poi le moltiplicazioni e la somma algebrica come nei precedenti casi:

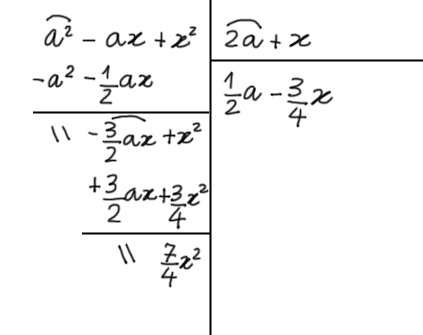
A questo punto ci fermiamo poiché il grado del resto rispetto ad {a} è minore del grado rispetto ad {a} del divisore. Abbiamo così ottenuto in conclusione:

Q(a)=\dfrac{a}{2}-\dfrac{3}{4}x; \qquad R(a)=\dfrac{7}{4}x^2

Effettivamente il quoziente e il resto ottenuti sono differenti rispetto a quelli relativi alla stessa divisione eseguita però con riferimento alla lettera {a}:

Q(x)=x-3a; \qquad R(x)=7a^2

Ciò può sembrare strano poiché la divisione è la stessa e ci aspetteremo lo stesso risultato. Tuttavia, ragioniamo con il teorema di esistenza ed unicità del quoziente e del resto. Per tale teorema come sappiamo il quoziente e il resto ottenuti dovranno essere tali che:

{Q(x) \cdot D(x)+R(x) = P(x)}

ove al posto della {x} considereremo di volta in volta la lettera scelta come variabile di riferimento per la divisione.

Per il quoziente e il resto ottenuti rispetto alla lettera {x} abbiamo:

\begin{align*} & (x-3a) \cdot (x+2a)+7a^2= \\ \\ & =x^2-3ax+2ax-6a^2+7a^2=\\ \\ & =x^2-ax+a^2\end{align*}

e ritroviamo il dividendo. Vediamo se succede la stessa cosa con il quoziente e il resto calcolati rispetto alla lettera {a}:

\begin{align*} & \left( \dfrac{a}{2}-\dfrac{3}{4}x\right)(2a+x)+\dfrac{7}{4}x^2 = \\ \\ & =a^2-\dfrac{3}{2}ax+\dfrac{1}{2}ax-\dfrac{3}{4}x^2+\dfrac{7}{4}x^2= \\ \\ & =a^2-ax+x^2= x^2-ax+a^2\end{align*}

Effettivamente ritroviamo ancora il dividendo. Di conseguenza entrambe le coppie quoziente e resto rispetto alle lettere {a} e {x} rispettano le condizioni del teorema di esistenza e unicità del quoziente e del resto per la divisione tra polinomi. E ciò ci rende giustizia del fatto che le due coppie si riferiscono alla stessa divisione.

Conclusioni

Per quanto riguarda la divisione tra polinomi è tutto. L’operazione non è così complicata come potrebbe sembrare. Il trucco è esercitarsi molto ed applicare correttamente tutte le regole. In particolare:

• ricordare sempre di ordinare i polinomi rispetto alla lettera scelta per la divisione (o rispetto all’unica lettera presente se i polinomi hanno una sola lettera);
• scrivere sempre in forma completa il polinomio dividendo, anche a costo di aggiungere dei termini con coefficiente zero;
• tenere conto che la divisione dovrà fermarsi quando il grado dell’ultimo resto parziale rispetto alla lettera scelta per la divisione (o all’unica presente) è minore del grado del divisore rispetto alla lettera scelta o all’unica lettera presente.

Per questa lezione è tutto. Nella prossima ci occuperemo di due importanti teoremi che riguardano un particolare caso della divisione tra polinomi: il teorema del resto e il teorema di Ruffini. Buono studio!