Ci occupiamo ora di domini piani delimitati da rette, ovvero di particolari regioni del piano aventi per “confini” delle rette (domini piani compresi tra rette). I domini piani dei quali discuteremo nel corso della lezione sono l’angolo, la striscia ed il poligono.
Nell’introdurre i domini piani e nel fornirne la rappresentazione analitica (ovvero descriverli mediante disequazioni) si rivelerà fondamentale quanto appreso nella precedente lezione relativamente alle disequazioni lineari in due incognite. In particolare, ciascuna disequazione lineare in due incognite rappresenta una regione di piano (in questo caso un semipiano). E, come vedremo nel corso della presente lezione, l’intersezione tra due semipiani può determinare a sua volta un angolo oppure una striscia. Invece, l’intersezione fra tre o più semipiani può determinare un poligono.
Osserviamo infine prima di dare il via alla lezione che i domini piani dei quali ci occuperemo sono tutti dati dall’intersezione di enti geometrici, e di conseguenza sono rappresentati da un sistema di disequazioni, ove ciascuna disequazione descrive il corrispondente ente geometrico.
Come rappresentare analiticamente alcuni domini piani
Angolo
Consideriamo un semipiano {\alpha_1} rappresentato dalla disequazione lineare in due incognite:
a_1 x +b_1y + c_1 \lesseqgtr 0
ove il simbolo “{\lesseqgtr}” indica un generico simbolo di disuguaglianza. Consideriamo inoltre un semipiano {\alpha_2} rappresentato dalla disequazione (lineare in due incognite):
a_2x+b_2y+c_2 \lesseqgtr 0
Ai due semipiani corrispondono rispettivamente le rette di equazioni:
a_1x+b_1y+c_1=0; \qquad a_2x+b_2y+c_2=0
Ciascuna equazione viene ottenuta uguagliando a zero il primo membro delle precedenti disequazioni.
Le rette rappresentate da tali equazioni sono le origini rispettivamente del semipiano {\alpha_1} e {\alpha_2}. Infatti è ciascuna di queste rette che separa il corrispondente semipiano dalla rimanente regione del piano.
Ora, supponiamo che le due rette siano tra loro incidenti. Con ciò, avendo a che fare con rette del piano (e non dello spazio), intendiamo che le rette sono tra loro non parallele e di conseguenza hanno un punto in comune.
Sotto tale ipotesi, l’intersezione tra i due semipiani {\alpha_1} e {\alpha_2} rappresenta una particolare regione di piano indicata con il nome di angolo. In simboli, scriviamo che l’intersezione tra due semipiani {\alpha_1} e {\alpha_2} è data da un certo angolo {\omega} come segue:
\omega = \alpha_1 \cap \alpha_2
e tenendo conto delle disequazioni che rappresentano ciascun semipiano:
\omega = \alpha_1 \cap \alpha_2:\begin{cases} a_1x+b_1y+c_1 \lesseqgtr 0 \\ \\ a_2x+b_2y+c_2 \lesseqgtr 0\end{cases}Ma affinché la regione di piano che si ottiene sia effettivamente un angolo deve valere la condizione di non parallelismo tra le due rette. Per esprimerla, proviamo anzitutto a riscrivere in forma esplicita ciascuna equazione delle rette origine dei semipiani (ipotizziamo {b_1 \neq 0 } e {b_2 \neq 0}):
\begin{align*} & a_1x+b_1y+c_1=0 \quad \Rightarrow \quad y=\dfrac{-a_1x-c_1}{b_1}\\ \\ &\Rightarrow y=-\dfrac{a_1}{b_1}-\dfrac{c_1}{b_1} \\ \\ & a_2x+b_2y+c_2=0 \quad \Rightarrow \quad y=\dfrac{-a_2x-c_2}{b_2} ;\\ \\ &\Rightarrow y = -\dfrac{a_2}{b_2}x-\dfrac{c_2}{b_2} \end{align*}Abbiamo così ottenuto per ciascuna retta un’equazione della forma {y=mx+q}, con {m_1=-\dfrac{a_1}{b_1}} e {m_2=-\dfrac{a_2}{b_2}}.
Ricordando che {m_1} e {m_2} rappresentano i coefficienti angolari di ciascuna retta, affinché le due rette non siano parallele dovrà essere:
m_1 \neq m_2 \iff -\dfrac{a_1}{b_1} \neq -\dfrac{a_2}{b_2} \iff \dfrac{a_1}{b_1} \neq \dfrac{a_2}{b_2}Infatti affinché due rette non siano parallele i rispettivi coefficienti angolari (che sono legati alla loro pendenza) devono essere diversi tra loro. Tale condizione assicura infatti una differente pendenza tra le rette, e quindi il loro non parallelismo.
Ora, la condizione ottenuta:
\dfrac{a_1}{b_1} \neq \dfrac{a_2}{b_2} \qquad (*)può essere riscritta come:
a_1 \cdot b_2 \neq a_2 \cdot b_1 \qquad (**)
Per rendersene conto, basta ricordare che in una proporzione il prodotto dei medi è uguale al prodotto degli estremi. Ed in questo caso, poiché il simbolo di disuguaglianza tra i rapporti nella * fa si che non debba valere la proporzione, abbiamo che il prodotto tra i medi è diverso dal prodotto tra gli estremi.
Ora, la ** può essere a sua volta riscritta come:
\underbrace{a_1 \cdot b_2 -a_2 \cdot b_1}_{\det \begin{pmatrix}a_1 & b_1 \\ a_2 & b_2 \end{pmatrix}} \neq 0 ovvero (per chi già conosce le matrici):
\det \begin{pmatrix} a_1 & b_1 \\ a_2 & b_2\end{pmatrix} \neq 0Tale condizione (in una delle ultime due forme scritte) assicura il non parallelismo tra le rette origine di ciascun semipiano {\alpha_1, \: \alpha_2}.
Dati due semipiani {\alpha_1} e {\alpha_2}, se questi hanno come origini delle rette tra loro non parallele, l’intersezione tra i due stessi semipiani determina un angolo {\omega= \alpha_1 \cap \alpha_2}.
In simboli:
\small \omega = \alpha_1 \cap \alpha_2 : \begin{cases} a_1x+b_1y+c_1 \lesseqgtr 0 \\ \\ a_2x +b_2y+c_2 \lesseqgtr 0\end{cases}\iff \det \begin{pmatrix} a_1 & b_1 \\ a_2 & b_2 \end{pmatrix} \neq 0Così l’angolo {\omega} è la regione di piano i punti della quale soddisfano entrambe le disequazioni a sistema, ovvero è la regione di piano costituita da punti tali da appartenere ad entrambi i semipiani {\alpha_1} ed {\alpha_2}.
Il nostro obiettivo, date le disequazioni relative ai semipiani {\alpha_1} e {\alpha_2}, è quello di rappresentare graficamente l’angolo {\omega}. Per fare questo, il primo passo è quello di determinare l’eventuale punto di intersezione tra le due rette origini dei semipiani {\alpha_1} e {\alpha_2}. Se tale punto esiste, sarà possibile determinare graficamente l’angolo {\omega} individuando la regione di piano nella quale si sovrappongono i due semipiani {\alpha_1} e {\alpha_2}. Ovviamente tale regione di piano è infinita e di conseguenza non potremo che rappresentarne una porzione.
Ma vediamo subito un esempio sui domini piani dati da angoli.
Esempio sui domini piani delimitati da rette del tipo “angolo”
Sono dati un semipiano {\alpha_1: 2x+3y -2\geq 0 } e un semipiano {\alpha_2:x-5y+1 < 0}. Rappresentare graficamente l’eventuale angolo {\omega} determinato dai due semipiani.
Prima di tutto, ricordiamo che affinché due semipiani possano determinare un angolo le rispettive rette di origine devono avere un punto in comune. In altre parole, le due rette devono essere incidenti.
Per quanto sin qui detto, le rette origine di ciascun semipiano sono:
2x+3y -2=0, \qquad x-5y+1=0
Confrontiamo le equazioni appena scritte con la loro forma generale:
a_1x+b_1y+c_1=0, \qquad a_2x+b_2y+c_2=0
da ciò deduciamo immediatamente:
a_1=2, \: b_1=3, \qquad a_2=1, \: b_2 = -5
Le due rette nel piano sono non parallele e quindi incidenti se e solo se:
a_1 \cdot b_2 - a_2 \cdot b_1 \neq 0
Nel nostro caso:
2 \cdot (-5) \neq 1 \cdot 3 \quad \Rightarrow \quad -10 \neq 3 \quad \text{vero}La disuguaglianza è vera e di conseguenza le due rette sono incidenti. Di conseguenza, poiché stiamo lavorando nel piano (e quindi le rette giacciono nello stesso piano) esiste necessariamente un punto in comune ad entrambe le rette (punto di intersezione). Per determinare tale punto, basta mettere a sistema le equazioni delle rette:
\begin{cases} 2x+3y -2=0 \\ \\ x-5y+1=0\end{cases}Risolviamo il sistema ad esempio per riduzione:
\small \begin{cases} 2x+3y-2=0 \\ \\ 2x-10y+2=0\end{cases} \quad \Rightarrow \quad \begin{cases} 2x+3y-2=0 \\ \\ 13y-4=0\end{cases} \quad \Rightarrow \quad \begin{cases}x=\left( 2-\dfrac{12}{13}\right) \cdot \dfrac{1}{2}= \dfrac{7}{13}\\ \\ y=\dfrac{4}{13}\end{cases}Di conseguenza il punto {T=\left( \dfrac{7}{13}, \dfrac{4}{13}\right)} è il punto di intersezione tra le due rette origini rispettivamente dei piani {\alpha_1} e {\alpha_2}.
Cominciamo rappresentando graficamente le due rette e il loro punto di intersezione nel piano cartesiano. Per fare questo ci basta determinare due punti qualsiasi appartenenti a ciascuna retta. Scriviamo le equazioni delle rette in forma esplicita:
y=\dfrac{2-2x}{3}, \qquad y=\dfrac{x+1}{5}Ponendo ad esempio {x=0} in ciascuna equazione otteniamo rispettivamente i due punti:
\small y = \dfrac{2}{3} \quad \Rightarrow \quad P_1=\left( 0, \dfrac{2}{3}\right), \qquad y = \dfrac{1}{5} \quad \Rightarrow \quad P_2=\left( 0,\dfrac{1}{5}\right)Così la retta origine del semipiano {\alpha_1} passerà per i punti {P_1} e {T}, mentre la retta origine del semipiano {\alpha_2} passerà per i punti {P_2} e {T} (disegno qualitativo):
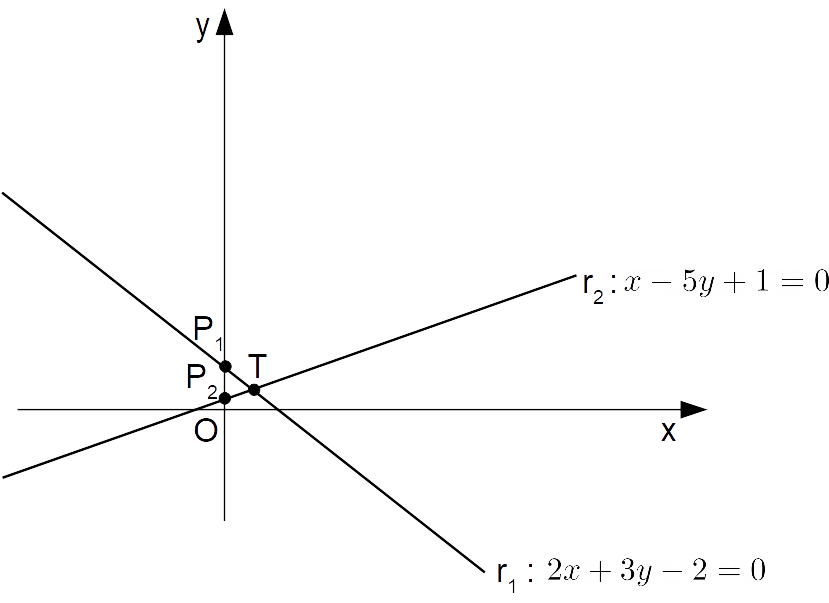
Ora non resta che rappresentare i due semipiani {\alpha_1} e {\alpha_2}, dati rispettivamente dalle disequazioni {2x+3y -2\geq 0} e {x-5y+1 < 0}.
Ripetendo le procedure viste nella lezione precedente, cominciamo determinando il piano {\alpha_1}. Ricordiamo che una retta divide il piano in due semipiani. Consideriamo allora la sola retta {r_1}. Questa determina nel piano i due semipiani {\beta_1} e {\beta_2}:
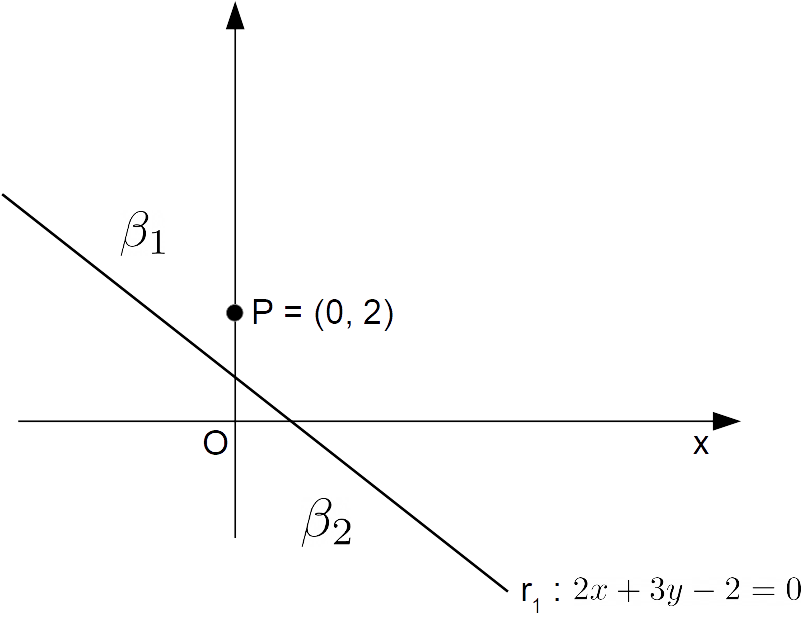
Come indicato in figura, prendiamo un punto {P} appartenente al semipiano {\beta_1}, e vediamo se soddisfa la disequazione relativa al semipiano {\alpha_1}:
2x+3y -2\geq 0 \: \text{ con } \: x=0, \: y=2 \quad \rightarrow \quad 4 \geq 0 \quad \text{OK}Quindi il semipiano {\alpha_1} coincide con {\beta_1}. Rappresentiamo tale semipiano nella figura ove sono presenti entrambe le rette {r_1} ed {r_2}:
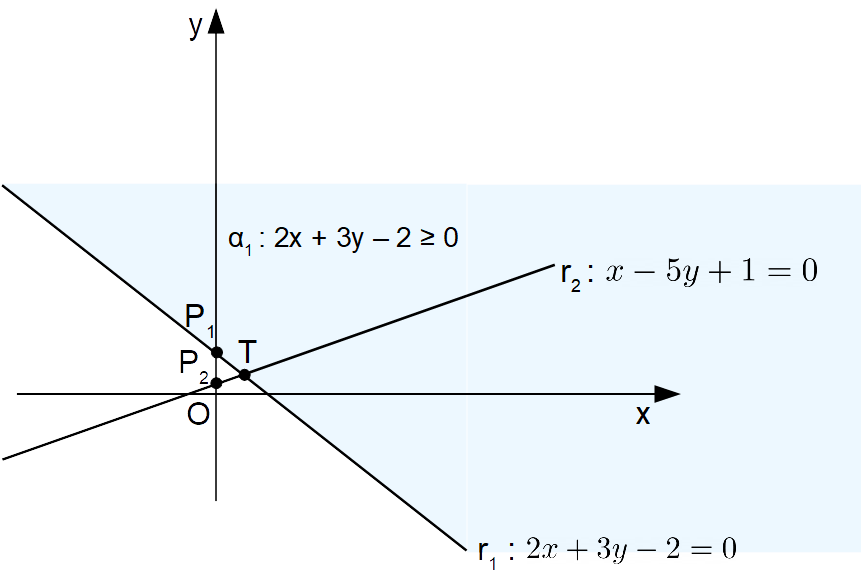
Ora resta da individuare il semipiano {\alpha_2}. Concentriamoci come fatto in precedenza sui due possibili semipiani che determina la retta {r_2}:
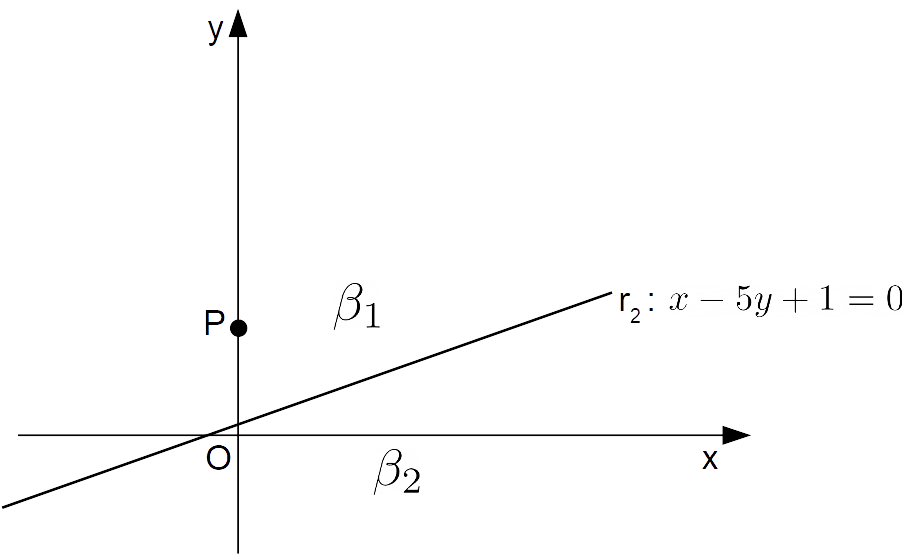
Dobbiamo così determinare quale dei due semipiani coincide con {\alpha_2}.
Considerando di nuovo il punto {P=(0,2)} appartenente al piano {\beta_1}, otteniamo sostituendo le coordinate del punto {P} nella disequazione relativa al piano {\alpha_2}:
x-5y+1 < 0 \: \text{ con } \: x=0, \: y = 2 \quad \rightarrow \quad -9<0 \quad \text{OK}Così il piano {\alpha_2} coincide con {\beta_1}:
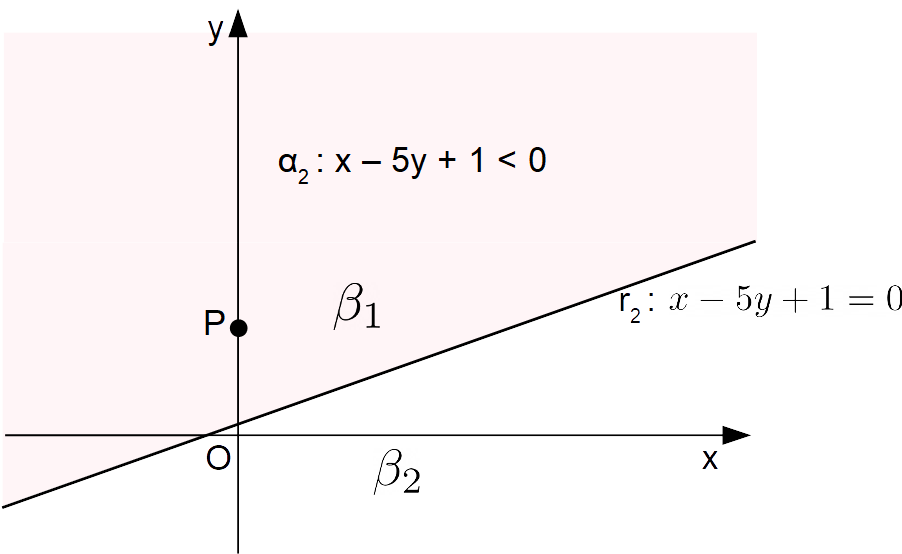
Quindi tornando al grafico con le due rette {r_1} ed {r_2} ci ritroviamo con la seguente situazione:
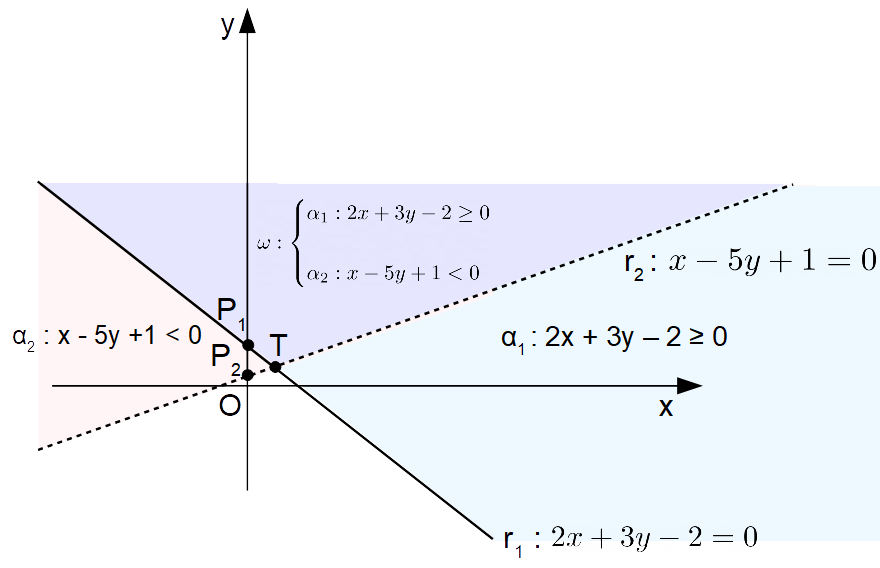
In particolare, una parte del semipiano {\alpha_2} (in rosa) è nascosta dal semipiano {\alpha_1}. Tale parte nascosta, indicata in viola, è proprio l’angolo {\omega} cercato.
E’ qui importante rilevare che nessun punto della retta {r_2} appartiene al dominio piano appena individuato. Ciò è dovuto alla presenza del simbolo di disuguaglianza stretta (“minore” e non “minore o uguale”) relativamente alla disequazione corrispondente al semipiano {\alpha_2}. Invece, i punti della semiretta avente origine in {T} e passante per {P_1} appartengono all’angolo {\omega}.
In conclusione, l’angolo {\omega} è dato da tutti i punti interni dell’angolo avente per lati le semirette aventi origine in {T} e passanti rispettivamente per i punti {P_1} e {P_2}, più tutti i punti della semiretta con origine in {T} e passante per {P_1}.
Striscia
Proseguiamo lo studio dei domini piani delimitati da rette introducendo un particolare dominio piano denominato striscia.
Consideriamo due rette giacenti nel piano cartesiano e parallele tra loro. Indichiamo tali rette con {r_1} ed {r_2}:
\small r_1: a_1x+b_1y+c_1=0, \qquad r_2=a_2x+b_2y+c_2=0
Ciascuna retta individua nel piano cartesiano due possibili semipiani:
\alpha_1 : a_1x+b_1y+c_1 \lesseqgtr 0, \qquad \alpha_2: a_2x+b_2y+c_2 \lesseqgtr 0
Osserviamo che in generale l’intersezione tra i due semipiani può essere vuota, coincidere con uno dei due semipiani oppure può essere data da una striscia {\sigma} delimitata dalle due rette {r_1} e {r_2}. Ciò dipende dalla posizione di una retta rispetto all’altra (la retta {r_1} può trovarsi “sopra” o “sotto” la retta {r_2}) e dalle disequazioni che individuano i semipiani {\alpha_1} e {\alpha_2}.
Infine, è da rilevare che la condizione di parallelismo tra le due rette {r_1} ed {r_2} è data da:
\det \begin{pmatrix} a_1 & b_1 \\ a_2 & b_2\end{pmatrix}=a_1 \cdot b_2 - a_2 \cdot b_1=0Consideriamo subito un esempio.
Esempio sui domini piani delimitati da rette del tipo “striscia”
Dati i due semipiani {\alpha_1 : 2x+5y-9 \leq 0} e {\alpha_2: 2x+5y+5 \geq 0} determinare se possibile il dominio piano dato dalla loro intersezione.
Le rette origine di ciascun semipiano sono rappresentate analiticamente come:
r_1 : 2x+5y-9 = 0, \qquad r_2: 2x+5y+5=0
Controlliamo la condizione di parallelismo tra le due rette:
a_1 \cdot b_2 - a_2 \cdot b_1 = 2 \cdot 5 - 5 \cdot 2 =0
Le due rette risultano parallele. Di conseguenza, dall’intersezione tra i due semipiani ci aspettiamo di ottenere, eventualmente, una striscia.
Procedendo come nell’esercizio precedente, a questo punto si tratta di rappresentare graficamente i semipiani {\alpha_1} e {\alpha_2} corrispondenti a ciascuna disequazione di partenza.
Per il semipiano {\alpha_1 : 2x+5y-9 \leq 0} abbiamo:
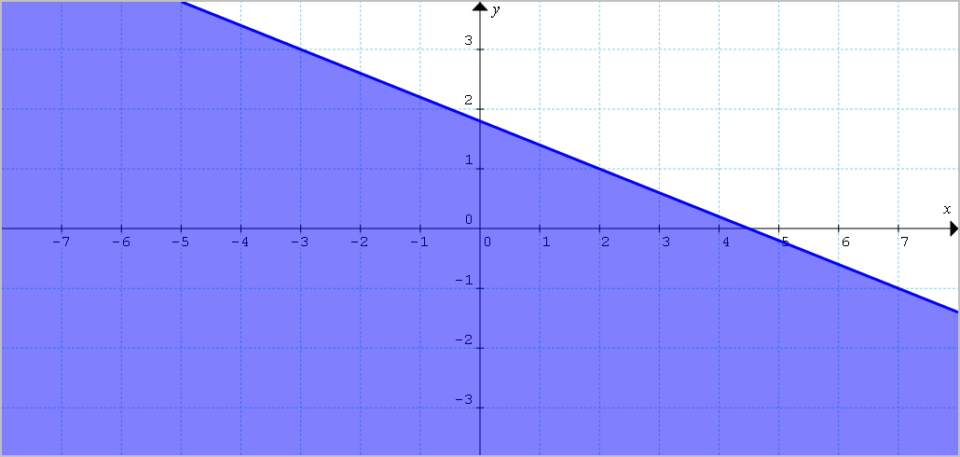
Mentre per il semipiano {\alpha_2: 2x+5y+5 \geq 0}:
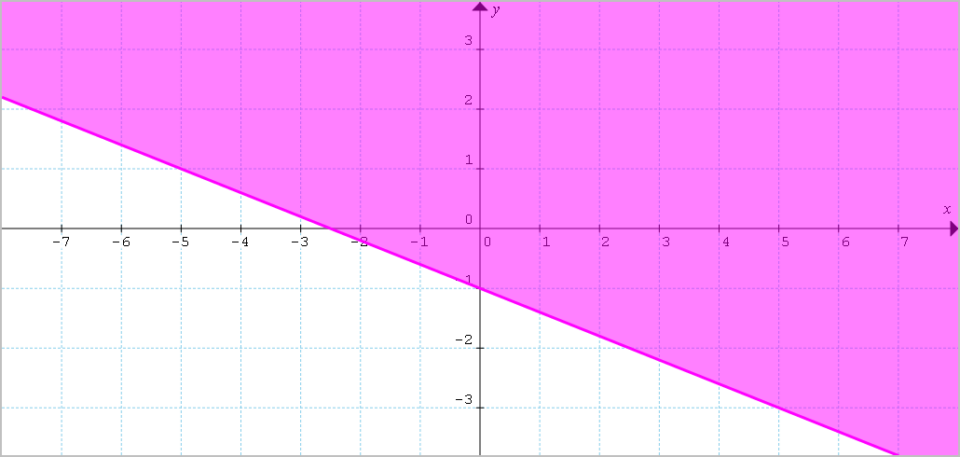
Poiché la retta {r_1} è al di sopra della retta {r_2}, e visti i simboli di disuguaglianza presenti nelle disequazioni di partenza, dall’intersezione tra i due semipiani otteniamo la seguente striscia {\sigma}:
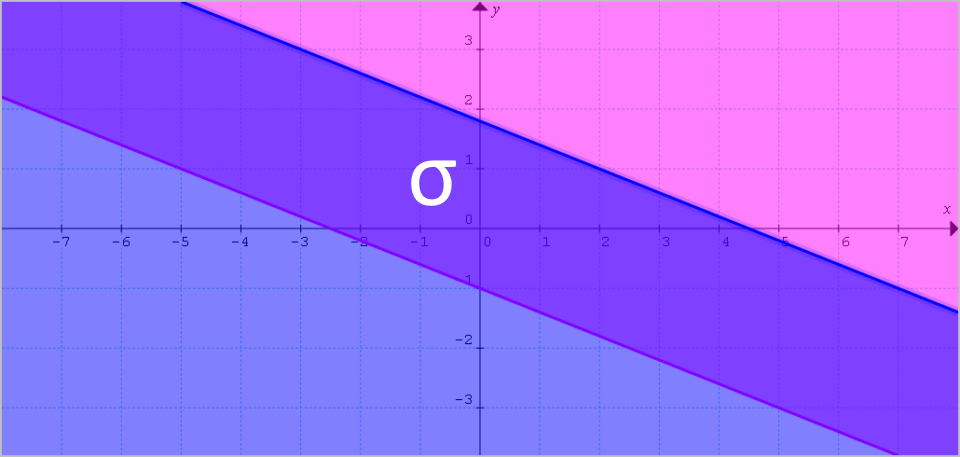
Osserviamo che il dominio piano ottenuto, ovvero la striscia {\sigma} in figura, è dato da tutti i punti della regione compresa tra le due rette {r_1} e {r_2}, inclusi anche i punti appartenenti a tali rette. Infatti, nelle disequazioni di partenza è compresa anche l’uguaglianza.
Poligono
Consideriamo a conclusione della lezione domini piani delimitati da rette del tipo “poligono”. In particolare ci occuperemo di domini piani dati da triangoli e da quadrilateri.
Come nei casi precedenti, tali domini piani si ottengono come intersezioni di semipiani (in questo caso almeno tre).
Il primo passo consiste nel tracciare le rette origini di ciascun semipiano.
Esempio 1 (domini piani delimitati da rette: triangolo)
Rappresentare il dominio piano risultante dall’intersezione dei semipiani {\alpha_1 : x+y -6 \leq 0}, {\alpha_2 : x \geq 0} e {\alpha_3: y \geq 0}.
Il metodo da seguire è del tutto simile a quello degli esercizi precedenti. Cominciamo tracciando le rette origini rispettivamente dei semipiani {\alpha_1, \: \alpha_2 } e {\alpha_3}. Come sempre, ricordiamo che è conveniente esprimere le equazioni delle rette in forma implicita (in questo caso tale accorgimento riguarda soltanto l’equazione origine del semipiano {\alpha_1}):
\begin{align*} &r_1 : x+y -6 = 0 \quad \Rightarrow \quad y=-x+6 \\ \\ & r_2 : x=0, \qquad r_3: y=0 \end{align*}Otteniamo la seguente rappresentazione grafica:
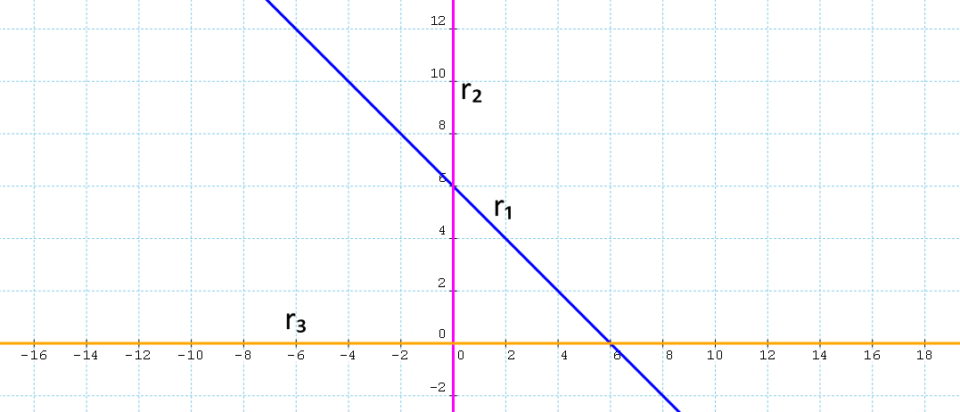
A questo punto consideriamo singolarmente ciascun semipiano. Per il semipiano {\alpha_1 : x+y -6 \leq 0 } abbiamo la seguente rappresentazione:
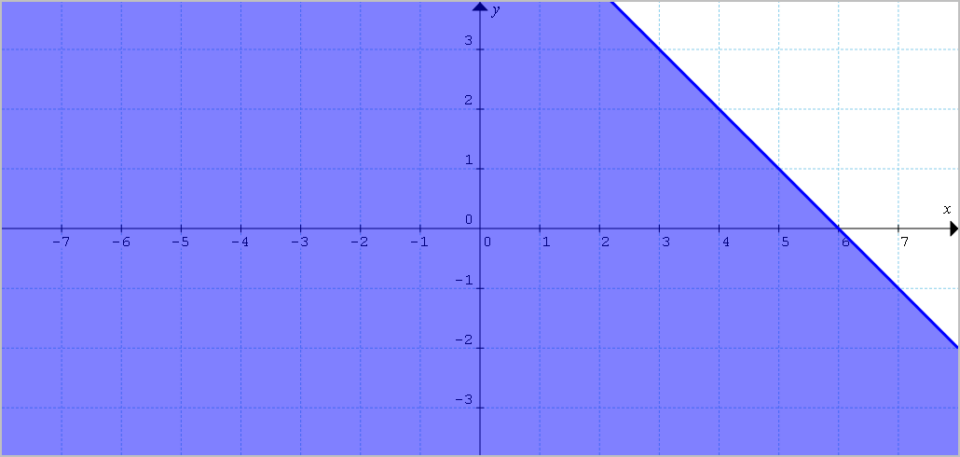
Si tratta in particolare di tutti i punti del piano che si trovano al di sotto della retta {r_1}.
Procediamo con la rappresentazione grafica del semipiano {\alpha_2 : x \geq 0}:
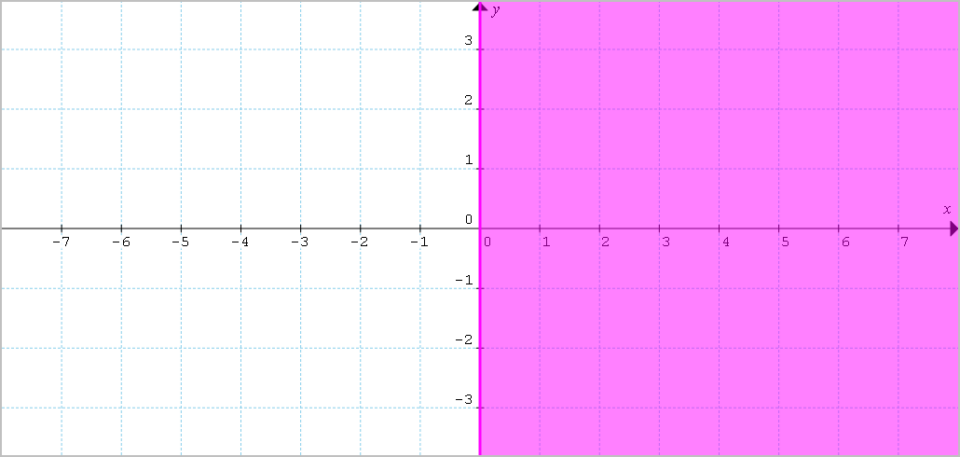
Si tratta in particolare di tutti i punti a destra dell’asse delle {y}.
Infine, concludiamo con il semipiano {\alpha_3: y \geq 0}:
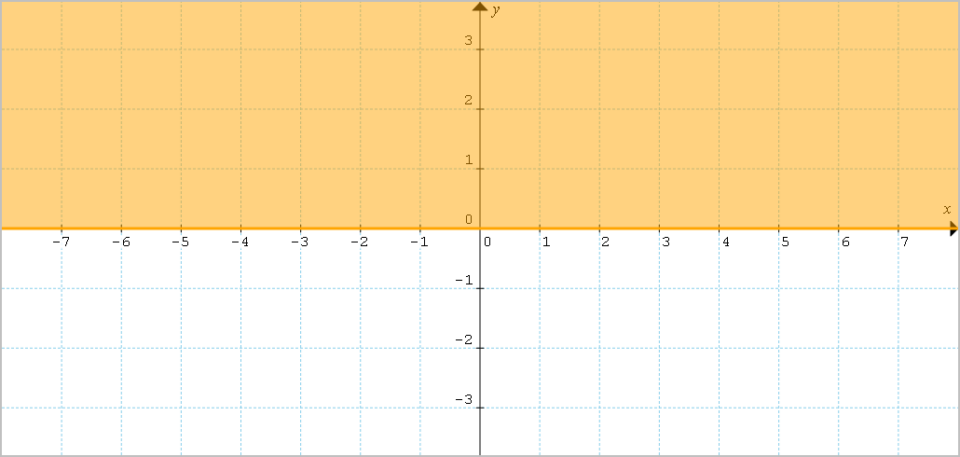
In questo caso abbiamo tutti i punti del piano cartesiano che si trovano al di sopra dell’asse delle {x}.
Il dominio piano {\tau} delimitato da rette che risulta dall’intersezione dei tre semipiani è dato analiticamente da:
\tau : \begin{cases} x+y -6 \leq 0 \\ \\ x \geq 0 \\ \\ y \geq 0\end{cases}Abbiamo in particolare un sistema ove ciascuna disequazione rappresenta uno dei tre precedenti semipiani.
Infine, il dominio {\tau} è rappresentabile graficamente come segue:
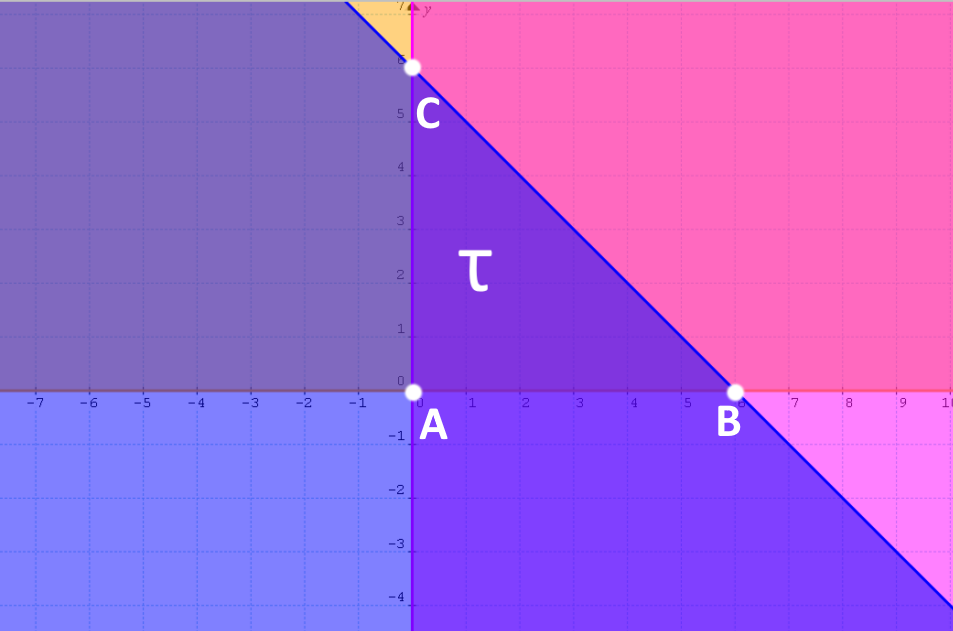
Il dominio piano {\tau} è in particolare dato da un triangolo rettangolo (il triangolo {ABC}). Effettivamente tutti i punti del triangolo sono tali da rispettare tutte e tre le disequazioni presenti nel precedente sistema. Abbiamo infatti tutti i punti al di sotto della retta {r_1} e tali da essere a destra dell’asse {y} e al di sopra dell’asse {x}.
Esempio 2 (domini piani delimitati da rette: quadrilatero)
Consideriamo il dominio piano dato dal quadrilatero {\rho}:
\rho : \begin{cases} 2x+3y+5 \geq 0 \\ \\ \dfrac{5}{2}x+3y-2 \leq 0 \\ \\ -x+3y+2 \geq 0 \\ \\ -x+3y-3 \leq 0 \end{cases}Come nei precedenti esercizi, il punto di partenza sta nell’osservare che ciascuna disequazione a sistema è una disequazione lineare in due incognite tale da rappresentare un semipiano. Così, il dominio piano {\rho} si ottiene come intersezione dei quattro semipiani indicati analiticamente nel sistema.
Prima di tutto, tracciamo le rette {r_1, \: r_2, \: r_3 } ed {r_4} corrispondenti ai semipiani {\alpha_1 : 2x+3y+5 \geq 0 }, {\alpha_2 : \dfrac{5}{2}x+3y-2 \leq 0}, {\alpha_3 : -x+3y+2 \geq 0} e {\alpha_4 : -x+3y-3 \leq 0 }. Tali rette sono le origini di ciascun semipiano e sono date da {r_1 : 2x+3y+5 = 0 }, {r_2 : \dfrac{5}{2}x+3y-2 = 0 }, {r_3 : -x+3y+2 = 0 } e infine {r_4: -x+3y-3 = 0 }.
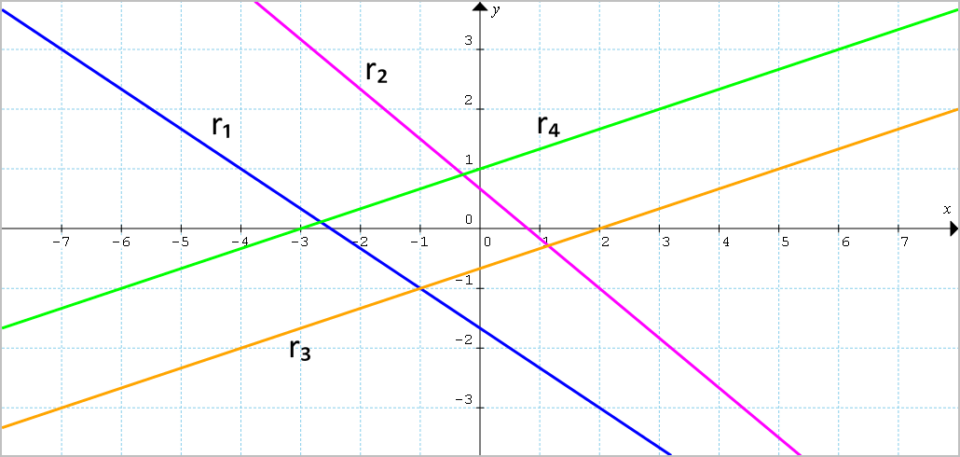
Dall’intersezione di tutti i semipiani otteniamo un quadrilatero:
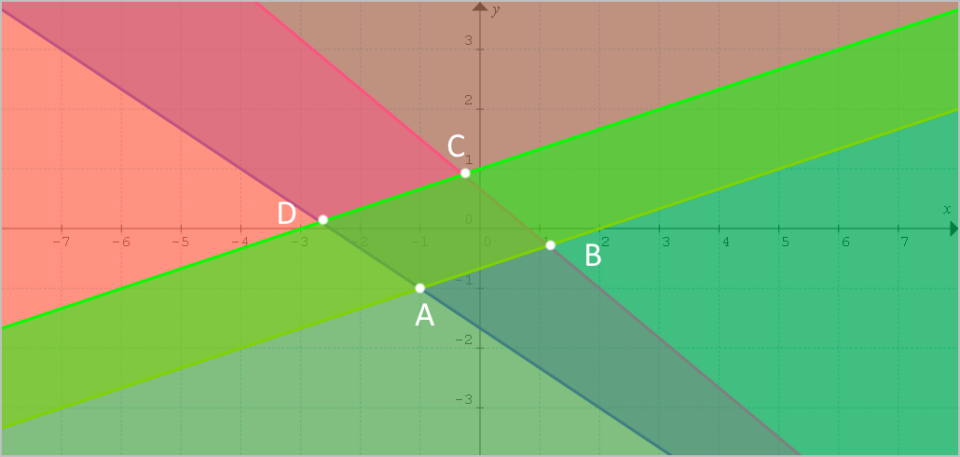
Per rendersene conto, basta considerare singolarmente ciascun semipiano e ragionare sui simboli di disuguaglianza presenti in ciascuna disequazione corrispondente. Si tratta in pratica dello stesso approccio visto nei precedenti esercizi.
In particolare, abbiamo l’insieme di tutti i punti del piano che stanno al di sopra di {r_1} e al di sotto di {r_2}, ed allo stesso tempo sopra {r_3} e sotto {r_4}. E’ da rilevare inoltre che i punti delle rette sono anch’essi compresi nel dominio piano, poiché in tutte le disequazioni relative ai semipiani è inclusa l’uguaglianza.
Il dominio piano {\rho} è pertanto dato dal quadrilatero {ABCD}.
Può anche essere di aiuto osservare che il quadrilatero {ABCD} si può ottenere dall’intersezione di due strisce, ciascuna determinata rispettivamente dalle coppie di semipiani {\alpha_1, \: \alpha_2} e {\alpha_3, \: \alpha_4}.
Osserviamo infine che ciascun vertice del quadrilatero si ottiene come intersezione delle coppie che è possibile formare a partire dalle rette {r_1, \: r_2, \: r_3} e {r_4}. Ad esempio, per il vertice {A}:
\begin{cases} r_3 : -x+3y+2 = 0 \\ \\ r_1 : 2x+3y+5 = 0 \end{cases}Risolviamo il sistema ad esempio per riduzione:
\begin{cases} -3x -3=0 \\ \\ 2x+3y+5= 0 \end{cases} \quad \Rightarrow \quad \begin{cases} x=-1 \\ \\ y=-1\end{cases}Di conseguenza abbiamo {A=(-1, -1)}. In modo del tutto simile è possibile determinare le coordinate dei rimanenti vertici.
Conclusioni
Per quanto riguarda i domini piani delimitati da rette è tutto. Abbiamo così visto come dall’intersezione di semipiani aventi per origini delle rette note è possibile ottenere sotto determinate condizioni dei domini piani.
Nella prossima lezione vedremo invece come sia possibile ottenere una semiretta oppure un segmento dall’intersezione di un opportuno dominio piano e di una retta. Buon proseguimento!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
