Equazione di una retta in forma implicita

 - 

Coordinate cartesiane e retta nel piano

L’equazione di una retta in forma implicita è della forma ax + by + c = 0, con a, b, c coefficienti reali e con a e b non contemporaneamente nulli. Tale equazione comprende tutte le possibili rette del piano cartesiano, comprese le rette parallele all’asse delle y. Infatti, mentre non è possibile ridurre l’equazione esplicita della retta y = mx + q alla forma x = k, ciò è invece possibile nel caso dell’equazione in forma implicita della retta, ponendo come vedremo b = 0.

Dunque, l’equazione di una retta in forma implicita consente di rappresentare una qualunque retta del piano cartesiano, comprese le rette parallele all’asse {y} (rette verticali), alle quali corrispondono equazioni nella forma {x=k}, con {k} coefficiente reale (è qui utile ricordare che una retta parallela all’asse delle {y} è costituita da punti aventi tutti la stessa ascissa).

L’equazione è detta “implicita” in quanto nella sua espressione non risulta esplicitata alcuna variabile. Invece, come abbiamo visto in una precedente lezione, nell’equazione di una retta in forma esplicita abbiamo la variabile {y} che è esplicitata rispetto alla variabile {x}. In altre parole, in quest’ultimo caso ci ritroviamo con un’equazione della forma {y= \text{espressione contenente la} \: x} (ovvero, come sappiamo, {y=mx+q}).

Nel corso della lezione mostreremo come è possibile passare dall’equazione di una retta in forma implicita alla corrispondente forma esplicita. Inoltre, data l’equazione di una retta in forma implicita vedremo come ricavare il coefficiente angolare e l’ordinata all’origine corrispondenti alla retta stessa.

Come scrivere l’equazione di una retta in forma implicita

L’equazione di una retta in forma implicita è data da un polinomio di primo grado nelle due variabili {x} e {y} uguagliato a zero:

ax+by+c=0

ove {a, \: b, \: c} sono coefficienti reali, con {a} e {b} mai nulli contemporaneamente.

In altre parole abbiamo la somma di un termine in {x}, di un termine in {y} e di un termine noto (numero), somma che viene uguagliata a zero. E i termini in {x} e {y} sono di primo grado.

La forma differisce da quella esplicita in quanto non abbiamo un’espressione di una variabile data in funzione dell’altra variabile. Ricordiamo che l’equazione in forma esplicita di una retta del piano cartesiano è della forma:

y=mx+q

ove {m} è il coefficiente angolare mentre {q} è l’ordinata all’origine. Come già sappiamo, il coefficiente angolare rende conto della pendenza della retta, ovvero dell’angolo che la retta forma con la direzione positiva dell’asse delle {x}. L’ordinata all’origine {q}, invece, rappresenta l’ordinata del punto di intersezione tra la retta considerata e l’asse delle {y}. Con parole più semplici, l’ordinata all’origine {q} è il valore della {y} che si ottiene ponendo {x=0} nell’equazione della retta in esame.

Esempio (equazione di una retta in forma implicita)

L’equazione:

2x-7y+4=0

è l’equazione di una retta in forma implicita. Infatti, l’equazione è della forma {ax+by+c=0} ove {a=2, \: b=-7} e infine {c=4}. Come è possibile vedere, nessuna variabile risulta esplicitata rispetto all’altra, ma abbiamo semplicemente un polinomio di primo grado nelle due variabili {x} e {y} uguagliato a zero.

Attenzione. L’equazione di una retta nel piano cartesiano può dunque essere scritta nelle due forme “normali” {ax+by+c=0} (forma implicita) e {y=mx+q} (forma esplicita). Ogni equazione rappresentante una retta ma scritta in forme differenti dalle due appena indicate può essere comunque ricondotta ad una delle due. Ci occupiamo di questo nell’esempio immediatamente a seguire.

Esempio (equazione di una retta in forma non normale)

L’equazione:

9y+3x=-5

non rispecchia propriamente nessuna delle tue tipologie di equazioni precedentemente indicate. Infatti, non abbiamo una variabile esplicitata rispetto all’altra ma allo stesso tempo il secondo membro è diverso da zero. In un caso di questo tipo è comunque possibile affermare che l’equazione è in forma implicita (infatti non è della forma {y=f(x)}). Sarebbe invece ovviamente errato affermare che l’equazione è in forma esplicita.

Vogliamo comunque ricondurci alla forma implicita così come in precedenza indicata. Allo scopo, è immediato osservare che trasportando il termine {-5} dal secondo membro al primo membro possiamo ricondurci all’equazione di una retta in forma implicita. Abbiamo infatti:

9y+3x+5=0

Ci ritroviamo ora con un polinomio di primo grado nelle due variabili {x} e {y} uguagliato a zero, che effettivamente corrisponde all’equazione di una retta in forma implicita.

Leggermente più complicato è invece ricondurre l’equazione data nell’esempio precedente alla forma esplicita. Di questo ci occuperemo immediatamente a seguire.

Passaggio dalla forma implicita alla forma esplicita dell’equazione di una retta nel piano

Vogliamo ora mostrare come si passa dall’equazione di una retta in forma implicita alla corrispondente equazione in forma esplicita. Partiamo dalla generica equazione di una retta in forma implicita:

ax+by+c=0, \qquad a, \: b, \: c \in \R

L’idea è quella di isolare al primo membro la variabile {y}. Per fare questo, cominciamo trasportando i termini che non contengono la {y} al secondo membro. Come sempre, nel trasportare i termini ricordiamo di cambiarne il segno:

by=-ax-c

Ora, supponendo {b \neq 0} è possibile dividere entrambi i membri per {b}, in forza del secondo principio di equivalenza delle equazioni:

\dfrac{by}{b}=\dfrac{-ax-c}{b}

Semplificando al primo membro ed applicando la proprietà distributiva della divisione rispetto alla somma algebrica al secondo membro abbiamo:

y=-\dfrac{a}{b}x-\dfrac{c}{b}

Ora, basta porre:

m=-\dfrac{a}{b}, \qquad q=-\dfrac{c}{b}

in tal modo la precedente equazione diviene:

y=mx+q

Abbiamo così visto come passare dalla forma implicita alla forma esplicita dell’equazione di una retta del piano cartesiano.

Ma vediamo subito un esempio pratico.

Esempio (passare dalla forma implicita alla forma esplicita di un’equazione di una retta del piano)

Riscrivere in forma esplicita la seguente equazione data in forma implicita: {-3x+4y-8=0}

Isoliamo al primo membro il termine in {y}. Per fare ciò basta trasportare al secondo membro i termini rimanenti, cambiandone il segno:

4y=3x+8

Concludiamo dividendo entrambi i membri per il coefficiente del termine in {y}, ovvero per {4}:

\dfrac{4}{4}y=\dfrac{3}{4}x+\dfrac{8}{4}

Semplificando otteniamo in conclusione:

y=\dfrac{3}{4}x+2

che è la forma esplicita dell’equazione data in partenza.

Il passaggio dalla forma esplicita alla forma implicita dell’equazione di una retta è ancora più semplice.

Passaggio dalla forma esplicita alla forma implicita dell’equazione di una retta nel piano

Data l’equazione di una retta in forma esplicita:

y=mx+q, \qquad m, \: q \in \R

questa può essere riespressa in forma implicita semplicemente portando tutti i termini al primo membro (come sempre, ricordiamo di cambiare il segno dei termini che trasportiamo):

y-mx-q=0

In questo modo l’equazione è già riscritta in forma implicita. In generale ove necessario sarà comunque opportuno ricondurre il polinomio di primo grado al primo membro nella forma a coefficienti interi.

Ma vediamo subito un esempio su come passare dall’equazione di una retta in forma esplicita alla corrispondente equazione in forma implicita.

Esempio (passaggio dalla forma esplicita alla forma implicita di un’equazione di una retta del piano)

Ricondurre alla forma implicita la seguente equazione di una retta, data in forma esplicita: {y=-\dfrac{3}{2}x+7}

Cominciamo trasportando tutti i termini al primo membro, ovviamente cambiandone il segno:

y+\dfrac{3}{2}x-7=0

Infine, moltiplichiamo tutti i termini per {2} in modo da liberarci dal denominatore presente nel coefficiente del termine in {x}:

2y+3x-14=0

L’equazione è ora correttamente espressa in forma implicita (la precedente equazione {y+\dfrac{3}{2}x-7=0} sarebbe stata comunque accettabile, anche se non “elegante”).

Condizione di appartenenza di un punto ad una retta

Rivediamo ora la condizione di appartenenza di un punto ad una retta nel caso in cui sia data l’equazione della retta stessa in forma implicita.

Consideriamo la generica equazione in forma implicita di una retta del piano cartesiano:

ax+by+c=0

Sia dato un punto {P=(x_0, y_0)} del piano cartesiano. Se tale punto appartiene alla retta in esame, allora dovrà essere verificata l’equazione:

ax_0+by_0+c=0

equazione che si ottiene sostituendo alla {x} nell’equazione della retta in esame l’ascissa {x_0} del punto {P}, e sostituendo alla {y} nella stessa equazione l’ordinata {y_0} sempre del punto {P}.

Così ad esempio il punto {P=(2,5)} appartiene alla retta di equazione:

y-2x-1=0

Infatti sostituendo l’ascissa e l’ordinata del punto {P} rispettivamente alla {y} e alla {x} nell’equazione appena scritta abbiamo:

5-2 \cdot 2 -1 = 0 \quad \Rightarrow \quad 0 = 0

Otteniamo l’identità {0=0}, per cui il punto {P} appartiene alla retta di equazione {y-2x-1 = 0}. Diversamente, il punto {P_1 = (2, -1)} non appartiene alla retta considerata. Infatti, sostituendo i valori delle coordinate del punto {P_1} nell’equazione della retta stessa otteniamo:

-1 -2 \cdot 2 -1 = 0 \quad \Rightarrow \quad -6 = 0

L’uguaglianza numerica ottenuta è falsa, e di conseguenza il punto {P_2} non appartiene alla retta di equazione {y-2x-1=0}.

L’equazione di una retta in forma implicita può rappresentare qualsiasi retta del piano cartesiano

Riprendiamo ancora l’equazione di una retta nel piano cartesiano in forma implicita:

ax+by+c=0, \qquad a,b,c \in \R

con {a,b} mai contemporaneamente nulli.

Abbiamo già visto che è possibile ricavare a partire dai coefficienti del polinomio al primo membro il coefficiente angolare e l’ordinata all’origine della retta in esame:

m=-\dfrac{a}{b}, \qquad q=-\dfrac{c}{b}

ove deve essere {b \neq 0}.

Ora, per quanto sappiamo sul coefficiente angolare, nel caso in cui sia {m \neq 0} avremo una retta con angolo {\alpha} maggiore di zero gradi, minore di {180} gradi e diverso da {90} gradi. In altre parole abbiamo, per ogni fissato valore di {m} diverso da zero, una retta non parallela né all’asse delle {x}, né all’asse delle {y}.

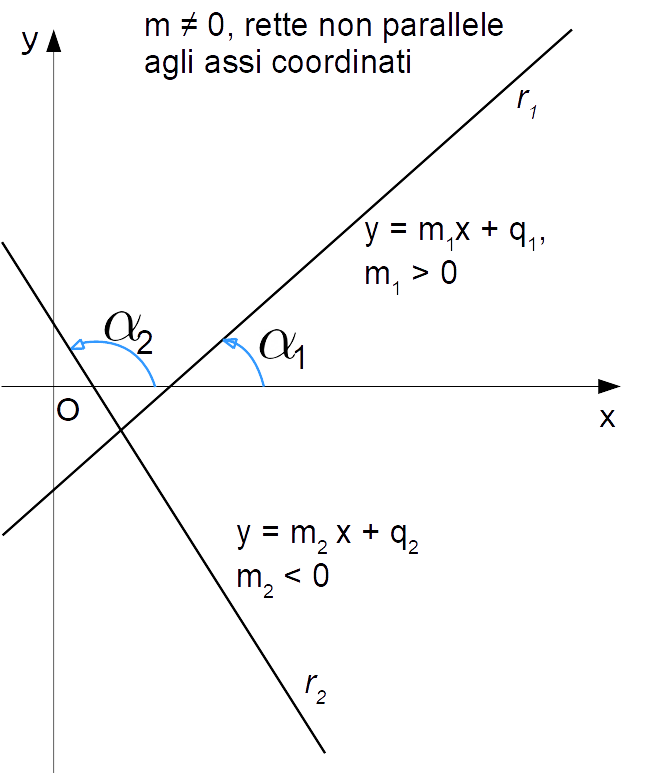
Ora, dato che {m=-\dfrac{a}{b}}, la condizione {m \neq 0} si ritraduce come:

-\dfrac{a}{b} \neq 0

ovvero, poiché {b \neq 0}:

a \neq 0

Per cui in conclusione per {a} e {b} entrambi diversi da zero ci ritroviamo, fissati {a} e {b}, con una retta che forma con la direzione positiva dell’asse delle {x} un angolo {\alpha} minore di 180 gradi e diverso da zero e da 90 gradi.

Nel caso in cui sia invece {a=0} e {b \neq 0}, l’equazione di una retta in forma implicita si riduce a:

by+c=0

ovvero passando alla forma esplicita:

y=-\dfrac{c}{b}

In questo caso ci ritroviamo con un’equazione della forma {y=k}, con {k} costante reale. E tale equazione corrisponde ad una retta parallela all’asse delle {x}. Infatti, tutti i punti di tale retta hanno lo stesso valore dell’ordinata. E l’angolo {\alpha} che la retta forma con la direzione positiva dell’asse delle {x} è uguale a zero gradi.

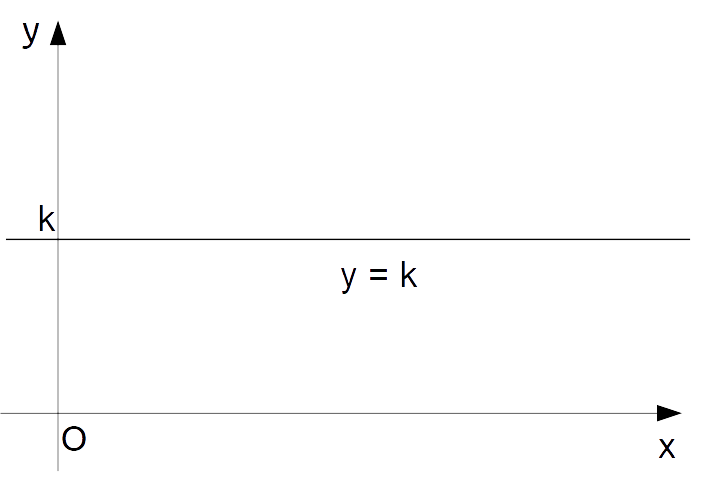
Infine, se anche {c=0} ci ritroviamo con l’equazione:

y=0

che rappresenta l’asse delle {x}.

Nel caso in cui sia invece {a \neq 0} e {b = 0} l’equazione della retta del piano in forma implicita diviene:

ax+c=0

da cui esplicitando la {x}:

ax=-c \quad \Rightarrow \quad x=-\dfrac{c}{a}

Ci ritroviamo così con un’equazione della forma {x=k}, con {k} costante reale, che corrisponde ad una retta parallela all’asse delle {y}. E l’angolo {\alpha} che la retta forma con la direzione positiva dell’asse delle {x} è in questo caso uguale a 90 gradi.

Infine, se anche {c=0} ci ritroviamo con l’equazione:

x=0

che rappresenta l’asse delle {y}.

In generale, se entrambi {a} e {b} sono diversi da zero ma {c} è uguale a zero, l’equazione implicita di una retta assume la particolare forma:

ax+by=0

e ci ritroviamo con l’equazione di una retta tale da non essere parallela agli assi coordinati e tale invece da essere passante per l’origine degli assi (retta con ordinata all’origine nulla). Ciò discende immediatamente dal fatto che per {c=0} l’ordinata all’origine {q=-\dfrac{c}{b}} è nulla.

E’ ora importante osservare che per {b=0} il coefficiente angolare {m} non è definito. Infatti, come già ricordato si ha {m=-\dfrac{a}{b}}, ma per {b=0} la frazione algebrica {-\dfrac{a}{b}} non ha significato.

Di conseguenza, l’equazione {y=mx+q} non può mai rappresentare una retta parallela all’asse delle {y}, per la quale deve invece essere {b=0}. Abbiamo così un’importante differenza tra le equazioni di una retta in forma implicita ed esplicita, come evidenzia la riflessione a seguire.

L’equazione di una retta in forma implicita, ovvero {ax+by+c=0}, con {a} e {b} mai contemporaneamente nulli, può anche rappresentare una retta parallela all’asse delle {y}. Infatti, ponendo {b=0} ci ritroviamo con l’equazione {ax+c=0} , ovvero {x=k} con {k=-\dfrac{c}{a}}.
Diversamente, per l’equazione in forma esplicita {y=mx+q} non esiste alcun valore di {m} tale da ricondurla alla forma {x=k}. Infatti, nel caso di una retta parallela all’asse delle {y} (retta verticale) si ha {b=0}. Ma per {b=0} il coefficiente angolare {m} non è definito.

Quindi, in conclusione, mentre l’equazione {y=mx+q} non può rappresentare rette verticali, l’equazione {ax+by+c=0} può rappresentare una qualunque retta del piano cartesiano, comprese le rette verticali.

Così riassumento, l’equazione {ax+by+c=0}:

• se {a=0} (e {b \neq 0}) diviene della forma {y=-\dfrac{c}{b}} ovvero {y=k} e rappresenta per ogni dato {k} una retta orizzontale (retta parallela all’asse delle {x});
• se {b=0} (e {a \neq 0}) diviene della forma {x=-\dfrac{c}{a}} ovvero {x=k} e rappresenta per ogni dato {k} una retta verticale (retta parallela all’asse delle {y});
• ancora, se entrambi {a} e {b} sono diversi da zero l’equazione al variare dei valori assunti dai coefficienti {a, b, c} rappresenta tutte le rimanenti rette del piano cartesiano (ovvero le rette non parallele agli assi coordinati);
• infine, come caso particolare del punto precedente, se entrambi {a} e {b} sono diversi da zero ma se {c=0} ci ritroviamo con rette non parallele agli assi coordinati e passanti per l’origine degli assi.

Come disegnare una retta a partire dalla sua equazione in forma implicita

Supponiamo di dover disegnare una retta sul piano cartesiano a partire dalla corrispondente equazione in forma implicita:

ax+by+c=0

Per fare questo è sufficiente riscrivere l’equazione in forma esplicita, isolando la {y} al primo membro (supponendo che sia {b \neq 0}):

y=-\dfrac{a}{b}x-\dfrac{c}{b}

A tal punto basta attribuire due differenti valori alla {x} (ad esempio {0} e {1}) e ricavare le {y} corrispondenti. Così facendo si otterranno le coordinate di due punti nel piano cartesiano. La retta cercata sarà quella che passa per entrambi i due punti.

Esempio

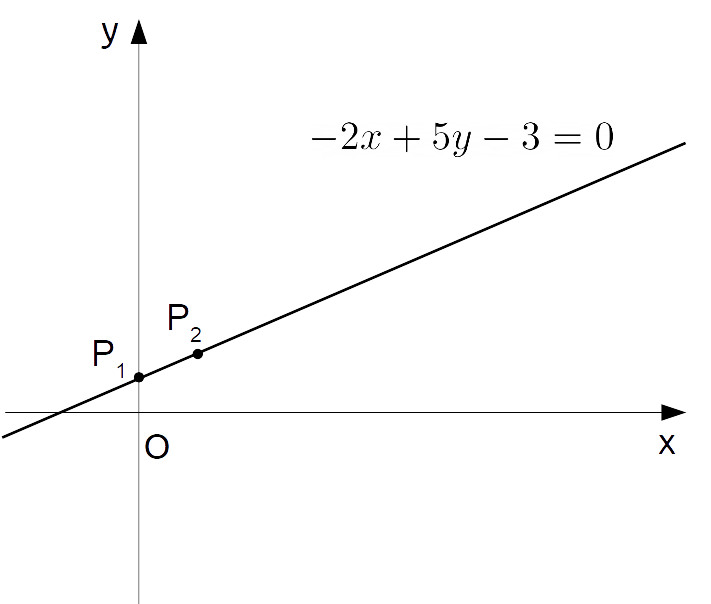
Disegnare la retta di equazione: {-2x+5y-3=0}

Passiamo all’equazione in forma esplicita:

-2x+5y-3=0 \quad \Rightarrow \quad 5y=2x+3 \quad \Rightarrow \quad y=\dfrac{2}{5}x+\dfrac{3}{5}

Per {x=0} sostituendo otteniamo {y=\dfrac{3}{5}}. Infine per {x=1} otteniamo {y=1}. Di conseguenza, i due punti {P_1=\left(0, \dfrac{3}{5}\right)} e {P_2 = \left( 1,1\right)} appartengono alla retta.

Infine non resta che rappresentare i due punti sul piano cartesiano e quindi tracciare la retta che passa per entrambi. Questa sarà la retta cercata.

Conclusioni

Per quanto riguarda questa lezione è tutto. Abbiamo quindi visto come si presenta l’equazione di una retta nel piano in forma implicita e come passare dalla forma implicita a quella esplicita e viceversa.

Nella prossima lezione vedremo come scrivere l’equazione di una retta del piano passante per due punti dei quali sono note le coordinate. Buon proseguimento a tutti voi! 🙂