Riprendiamo quanto visto nella precedente lezione sulla definizione di valore assoluto mostrando più nel dettaglio come risolvere le equazioni con valore assoluto, nei vari casi. Chi di voi ha già letto la precedente lezione avrà così modo di approfondire ulteriormente i metodi risolutivi delle equazioni con valore assoluto. Chi invece non ha letto la precedente lezione potrà comunque partire direttamente dalla presente. Infatti qui ci occuperemo un po’ di tutti gli aspetti relativi a questo tipo di equazioni, focalizzandoci sui metodi risolutivi. E per chi lo desidera, è sempre possibile consultare poi anche la lezione precedente, in modo da aver ancor più chiaro il legame tra la definizione di valore assoluto e i metodi risolutivi delle equazioni con valori assoluti.
Possiamo classificare le equazioni con valore assoluto nelle seguenti categorie:
- equazioni con un valore assoluto e un termine noto;
- equazioni con un valore assoluto e una funzione;
- equazioni date dall’uguaglianza tra due valori assoluti;
- equazioni con due o più valori assoluti più un termine noto o una funzione.
Così rispettivamente avremo le seguenti tipologie di equazioni con valore assoluto:
\begin{align*} & |p(x)|=k, \qquad |p(x)|=f(x), \qquad |p(x)|=|f(x)|, \\ \\ & |p(x)|+|q(x)|+ \dots =f(x), \quad k \in \mathbb{R} \end{align*}A volte le equazioni non si presentano esattamente nelle forme appena scritte, ma possono essere ad esse ricondotte mediante semplici manipolazioni algebriche. Ad esempio, l’equazione:
|p(x)|-|q(x)|=0
può essere ricondotta ad una delle precedenti forme trasportando il termine {-|q(x)|} al secondo membro:
|p(x)|=|q(x)|
Vediamo a questo punto come risolvere ciascuna delle equazioni nelle forme indicate. Precisiamo che i metodi risolutivi che illustreremo a seguire sono tutti basati sulla definizione di valore assoluto, vista nella precedente lezione.
Equazioni con un valore assoluto e termine noto
Consideriamo l’equazione in forma generica:
|p(x)|=k, \qquad k \in \mathbb{R}Se {k>0} le eventuali soluzioni dell’equazione si ottengono dall’unione degli insiemi delle soluzioni delle seguenti equazioni:
p(x)=k, \qquad p(x)=-k
Se invece {k < 0} l’equazione risulta impossibile.
Nel caso in cui invece sia {k = 0} l’equazione si riduce a {p(x)=0}.
Vediamo subito un paio di esempi su come risolvere un’equazione con un valore assoluto e un termine noto.
Esempio 1
Risolvere la seguente equazione:
|x^2-1|=2
Abbiamo {k>0} per cui le eventuali soluzioni dell’equazione saranno date dall’unione delle soluzioni delle equazioni:
x^2-1=2; \qquad x^2-1=-2
Per la prima equazione (vedi equazioni di secondo grado) abbiamo:
x^2-1=2; \qquad x^2-3=0; \qquad x_{1,2}=\pm\sqrt{3}Per la seconda equazione:
x^2-1=-2; \qquad x^2+1=0; \qquad \text{impossibile}Così in conclusione per l’equazione con valore assoluto di partenza abbiamo le due soluzioni:
x_{1}=\sqrt{3}; \qquad x_2=-\sqrt{3}Esempio 2
Risolvere la seguente equazione con modulo:
|3+2x-x^2|+4=0
Portiamo il termine noto al secondo membro in modo da ricondurci alla forma {|p(x)|=k}:
|3+2x-x^2|=-4
Concludiamo immediatamente che l’equazione è impossibile. Infatti abbiamo {k<0}. In alternativa, basta osservare che la quantità al primo membro è un valore assoluto e quindi una quantità positiva, che non potrà mai essere uguale alla quantità negativa al secondo membro.
Equazioni con un valore assoluto ed un’espressione funzione della {x}
Consideriamo ora equazioni della forma:
|p(x)|=f(x)
In questo caso non abbiamo più al secondo membro una costante ma un’espressione che è funzione della {x}. Dobbiamo allora ragionare con la definizione di valore assoluto. In particolare, le soluzioni dell’equazione saranno date dall’unione degli insiemi delle soluzioni dei seguenti sistemi:
\begin{cases}p(x) = f(x) \\ \\ p(x)\geq 0 \end{cases} \qquad \vee \qquad \begin{cases} -p(x)=f(x) \\ \\ p(x) < 0\end{cases}Vediamo subito un paio di esempi.
Esempio 3
Risolvere l’equazione con valore assoluto:
|4-2x|=1+x
Abbiamo:
\begin{cases} 4-2x=1+x \\ \\ 4-2x \geq 0 \end{cases} \qquad \vee \qquad \begin{cases}-(4-2x)=1+x \\ \\ 4-2x < 0 \end{cases}ovvero:
\begin{cases} -3x=-3 \\ \\ -2x \geq -4 \end{cases} \qquad \vee \qquad \begin{cases} -4+2x=1+x \\ \\ -2x<-4\end{cases}e quindi:
\begin{cases}x = 1 \\ \\ x \leq 2 \end{cases} \qquad \vee \qquad \begin{cases}x=5 \\ \\ x > 2 \end{cases}In ciascun sistema l’uguaglianza presente rispetta la sottostante disuguaglianza. Così entrambi i sistemi sono determinati e per l’equazione di partenza abbiamo le soluzioni:
x_1=1, \qquad x_2=5
Esempio 4
Vediamo ora come risolvere la seguente equazione con valore assoluto:
|x^2-1|=x
Si tratterà di unire le soluzioni dei seguenti sistemi:
\begin{cases}x^2-1=x \\ \\ x^2-1 \geq 0 \end{cases} \qquad \vee \qquad \begin{cases}-x^2+1=x \\ \\ x^2-1 < 0 \end{cases}Ovvero:
\begin{cases}x^2-1-x=0 \\ \\ x^2-1 \geq 0 \end{cases} \qquad \vee \qquad \begin{cases}-x^2+1-x=0 \\ \\ x^2-1 < 0 \end{cases}Si tratterà così di risolvere ciascuna equazione a sistema e verificare che rispetti la disequazione presente nel sistema corrispondente. Per l’equazione relativa al primo sistema:
x^2-x-1=0
utilizzando la formula risolutiva per le equazioni di secondo grado abbiamo:
x_{1,2}=\dfrac{1 \pm \sqrt{(-1)^2-4 \cdot 1 \cdot (-1)}}{2 \cdot 1}=\dfrac{1 \pm \sqrt{5}}{2}Veniamo ora alla condizione:
x^2-1 \geq 0
ovvero:
(x-1)(x+1) \geq 0
Abbiamo {x-1 \geq 0 } per {x \geq 1}. Inoltre abbiamo {x+1 \geq 0 } per {x \geq -1}. Studiando allora il segno del prodotto {(x-1)(x+1)} con l’aiuto di un diagramma si ha:
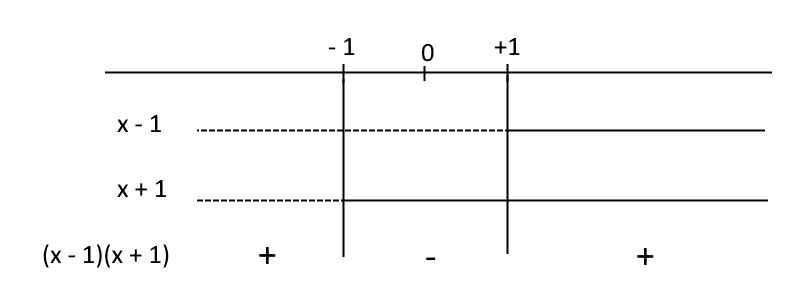
Così la condizione {x^2-1 \geq 0} è rispettata per {x \leq -1} e per {x \geq 1}. Una sola delle soluzioni dell’equazione a sistema rispetta tale condizione. Di conseguenza, abbiamo intanto per l’equazione con valore assoluto di partenza la soluzione {x_1 = \dfrac{1+ \sqrt{5}}{2}}.
Veniamo ora al secondo sistema. Consideriamo l’equazione:
-x^2-x+1=0
Applicando la formula risolutiva otteniamo le soluzioni:
x_{1,2}=\dfrac{1 \pm \sqrt{(-1)^2-4 \cdot (-1) \cdot 1 }}{2 \cdot (-1)}=\dfrac{1 \pm \sqrt{5}}{-2}=\dfrac{-1 \pm \sqrt{5}}{2}L’equazione è valida sotto la condizione {x^2-1 < 0}, ovvero per i valori della {x} interni agli zeri dell’equazione {x^2-1=0}. Così dovremo considerare le sole soluzioni dell’equazione tali da rispettare la condizione {- 1 < x < 1 }. E quindi potremo accettare come soluzione soltanto {x_2= \dfrac{-1+\sqrt{5}}{2}}.
In conclusione abbiamo per l’equazione con valore assoluto di partenza le soluzioni:
x_1=\dfrac{1+ \sqrt{5}}{2}, \qquad x_2=\dfrac{-1+\sqrt{5}}{2}delle quali una relativa al primo sistema ed una relativa al secondo sistema.
Equazioni con due valori assoluti (uguaglianza tra valori assoluti)
Consideriamo ora equazioni del tipo:
|p(x)|=|f(x)|
Come è immediato osservare abbiamo un’uguaglianza tra valori assoluti. In generale, due quantità sono uguali in valore assoluto se queste sono uguali oppure opposte. Di conseguenza le soluzioni dell’equazione data saranno uguali all’unione degli insiemi delle soluzioni delle equazioni:
p(x)=f(x) \quad \vee \quad p(x)=-f(x)
Vediamo subito degli esempi.
Esempio 5
Risolvere l’equazione:
|x+4|=|x^2-2x|
Le soluzioni dell’equazione sono date dall’unione dell’insieme delle soluzioni delle seguenti equazioni:
x+4=x^2-2x \qquad \vee \qquad x+4=-(x^2-2x)
ovvero:
x^2-3x-4=0 \quad \vee \quad -x^2+x-4=0
Per la prima equazione abbiamo:
x_{1,2}=\dfrac{3 \pm \sqrt{(-3)^2-4 \cdot 1 \cdot (-4)}}{2 \cdot 1}=\dfrac{3 \pm \sqrt{9+16}}{2}=\dfrac{3 \pm 5}{2}=\begin{cases} 4 \\ \\ -1\end{cases}Mentre per la seconda equazione:
\Delta = b^2-4ac=1-4 \cdot (-1)\cdot(-4)=1-16<0
Così la seconda equazione è impossibile ed abbiamo per l’equazione con valore assoluto di partenza le sole soluzioni:
x_1=4, \qquad x_2=-1
Esempio 6
Risolvere la seguente equazione con valori assoluti:
|x-3|=|4x+3|
Osservando come nel caso precedente che se due quantità sono uguali in valore assoluto allora queste sono uguali oppure opposte abbiamo:
x-3=4x+3 \quad \vee \quad x-3=-4x-3
Per la prima equazione abbiamo:
3x=-6 \quad \Rightarrow \quad x=-2
Mentre per la seconda equazione:
5x=0 \quad \Rightarrow \quad x=0
Così in conclusione per l’equazione di partenza abbiamo le soluzioni:
x_1=-2 \quad \qquad x_2 = 0
Equazioni con valori assoluti nei casi più generali
Consideriamo ora equazioni del tipo:
|p(x)|+|q(x)|+\dots=f(x)
ovvero equazioni dove compaiono due o più quantità entro il simbolo di modulo (valore assoluto) e un’espressione dipendente dalla {x}. Equazioni di questo tipo rappresentano il caso più generale di equazioni con valore assoluto.
Osservazione. Al posto dell’espressione {f(x)} possiamo avere in alternativa al secondo membro un termine costante {k \in \mathbb{R}}. Si tratta comunque sempre di un’espressione del tipo {f(x)} avente in tal caso grado zero.
L’idea è quella di eliminare i simboli di valore assoluto riscrivendo l’equazione per determinati intervalli di valori della {x}. E tali intervalli si individuano mediante lo studio del segno di ciascuna quantità presente all’interno del simbolo di valore assoluto. L’unione delle soluzioni di tutte le equazioni scritte rappresenterà l’insieme delle soluzioni dell’equazione con valore assoluto di partenza.
Esempio 7
Risolvere la seguente equazione con valori assoluti:
|5-2x|-|x-3|=x+4
Le quantità all’interno del simbolo di valore assoluto sono {5-2x} e {x-3}. Di queste quantità dovremo procedere allo studio del segno. Non dobbiamo invece studiare il segno della quantità {x+4} poiché non si trova all’interno dei simboli di valore assoluto (modulo).
Rappresentiamo lo studio del segno delle quantità indicate in uno stesso diagramma:
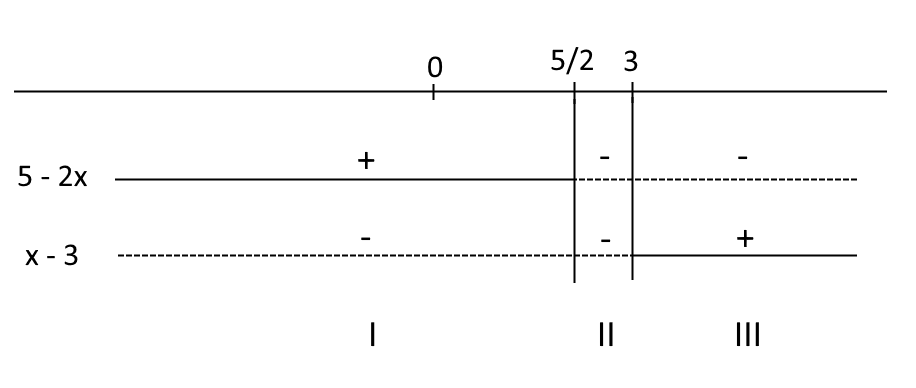
Come evidenzia il diagramma è possibile individuare tre distinti intervalli di valori assunti dalla {x}.
Gli intervalli devono essere scritti in modo da non avere elementi in comune tra loro. Così ad esempio se nel primo intervallo comprenderemo il valore {\dfrac{5}{2}}, questo andrà escluso nel secondo intervallo e viceversa. In altre parole, gli intervalli che scriveremo dovranno costituire una partizione dell’insieme dei numeri reali. Questa osservazione risulterà chiara osservando gli esempi.
Il primo intervallo è dato da {x \leq \dfrac{5}{2}}. In tale intervallo la quantità {5-2x} è positiva. Di conseguenza avremo {|5-2x|=5-2x}, ovvero potremo sostituire la quantità {|5-2x|} con la quantità {5-2x}. Ciò discende dalla definizione di modulo.
In modo del tutto simile, sempre nel primo intervallo osserviamo che la quantità {x-3} è negativa, e di conseguenza avremo {|x-3|=-(x-3)=-x+3}. Ciò significa che nel primo intervallo possiamo sostituire la quantità {|x-3|} con {-x+3}.
Dunque nel primo intervallo, ovvero sotto l’ipotesi {x \leq \dfrac{5}{2}}, l’equazione di partenza diviene:
5-2x-(-x+3)=x+4, \qquad x \leq \dfrac{5}{2}In pratica abbiamo eliminato i simboli di valore assoluto sfruttando la definizione di valore assoluto relativamente ad un certo insieme di valori della {x} (in particolare, i valori relativi al primo intervallo nel diagramma). Ricordando infatti che il valore assoluto forza positiva una quantità, è chiaro che se la quantità all’interno del simbolo di valore assoluto è positiva potremo lasciarla così come è, mentre se tale quantità è negativa dovremo invertire il segno di tutti i termini che la compongono. Ed infatti nell’equazione di partenza abbiamo sostituito {|5-2x|} con {5-2x} (eliminando soltanto i simboli di modulo), mentre abbiamo sostituito la quantità |x-3| con la quantità {-x+3}, invertendo i segni di tutti i termini che compongono la quantità stessa. Infatti nel primo intervallo abbiamo visto che la quantità {x-3} è negativa, e per forzarla positiva dobbiamo considerare la quantità ad essa opposta.
Ora non resta che vedere quale forma assume l’equazione nei rimanenti due intervalli.
Nel secondo intervallo possiamo vedere dal diagramma che entrambe le quantità all’interno dei simboli di modulo sono negative. Così l’equazione di partenza diviene in questo caso:
-5+2x-(-x+3)=x+4, \qquad \dfrac{5}{2} < x \leq 3Veniamo infine al terzo intervallo ({x > 3}). Qui possiamo vedere che la quantità {5-2x} è negativa mentre la quantità {x-3} è positiva. Di conseguenza abbiamo:
-5+2x-(x-3)=x+4, \qquad x > 3
Tenendo conto di tutte le equazioni sinora scritte e delle condizioni che le accompagnano, concludiamo che le soluzioni dell’equazione con valore assoluto di partenza saranno date dall’unione degli insiemi delle soluzioni dei seguenti sistemi, corrispondenti rispettivamente a ciascuno dei tre intervalli di valori della {x}:
\scriptsize\begin{cases} 5-2x+x-3=x+4 \\ \\ x \leq \dfrac{5}{2}\end{cases} \quad \vee \quad \begin{cases}-5+2x+x-3=x+4 \\ \\ \dfrac{5}{2} < x \leq 3 \end{cases} \quad \vee \quad \begin{cases} -5+2x-x+3=x+4 \\ \\ x>3 \end{cases}ovvero:
\begin{cases}x = -1 \\ \\ x \leq \dfrac{5}{2} \end{cases} \quad \vee \quad \begin{cases} x = 6 \\ \\ \dfrac{5}{2} < x \leq 3\end{cases} \quad \vee \quad \begin{cases}-2=4 \\ \\ x > 3 \end{cases}Evidentemente soltanto il primo sistema è determinato. Infatti, nel secondo sistema la soluzione {x=6} non rispetta la condizione relativa al secondo intervallo. Infine, nel terzo sistema l’uguaglianza {-2=4} è evidentemente impossibile.
Così in conclusione l’equazione con valore assoluto di partenza ammette la sola soluzione {x=-1}.
Esempio 8
Risolvere:
|1-4x|-|x^2-1|=4
Studiamo il segno delle quantità all’interno dei simboli di modulo. Osserviamo in particolare che la quantità {x^2-1} è positiva per valori della {x} esterni agli zeri dell’equazione {x^2-1=0}, ovvero esterni ai valori {-1} e {1}.
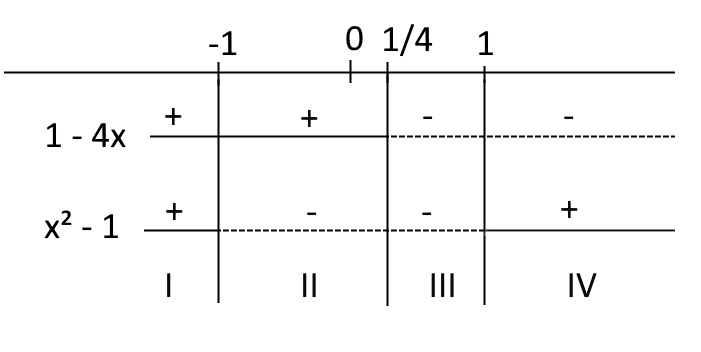
Ragionando su ciascun intervallo come nell’esempio precedente otteniamo i seguenti sistemi (nello scrivere ciascuna equazione attenzione a ragionare correttamente con i segni):
\scriptsize \begin{align*}&\begin{cases}1-4x-(x^2-1)=4 \\ \\ x \leq -1 \end{cases} \quad \vee \quad \begin{cases} 1-4x-(-x^2+1)=4 \\ \\ -1< x \leq \dfrac{1}{4}\end{cases} \quad \vee \\ \\ & \vee \quad \begin{cases} -(1-4x)-(-x^2+1)=4 \\ \\ \dfrac{1}{4} < x \leq 1 \\ \\ \end{cases} \quad \vee \quad \begin{cases}-(1-4x)-(x^2-1)=4 \\ \\ x > 1 \end{cases} \end{align*}e quindi:
\scriptsize \begin{align*} & \begin{cases}1-4x-x^2+1=4 \\ \\ x \leq -1 \end{cases} \quad \vee \quad \begin{cases}1-4x+x^2-1=4 \\ \\ -1 < x \leq \dfrac{1}{4} \end{cases} \quad \vee \\ \\ &\vee \quad \begin{cases}-1+4x+x^2-1=4 \\ \\ \dfrac{1}{4}< x \leq 1\end{cases} \quad \vee \quad \begin{cases} -1+4x-x^2+1=4 \\ \\ x > 1 \end{cases} \end{align*}ovvero:
\scriptsize \begin{align*} & \begin{cases}-x^2-4x-2=0 \\ \\ x \leq -1 \end{cases} \quad \vee \quad \begin{cases} x^2-4x-4 = 0 \\ \\ -1 < x \leq \dfrac{1}{4}\end{cases} \quad \vee \quad \begin{cases}x^2+4x-6=0 \\ \\ \dfrac{1}{4}< x \leq 1 \end{cases} \quad \vee \\ \\ & \vee \quad \begin{cases} -x^2+4x-4=0 \\ \\ x > 1 \end{cases} \end{align*}A questo punto non resta che risolvere ciascun sistema. Nella pratica si tratta di risolvere ciascuna equazione e verificare che rispetti la condizione per le {x} riportata nel sistema corrispondente. Risolvendo tali equazioni di secondo grado abbiamo:
\scriptsize \begin{align*} & \begin{cases}x_1 = -2-\sqrt{2}, \quad x_2=-2+\sqrt{2} \\ \\ x \leq -1\end{cases} \quad \vee \quad \begin{cases} x_1 = 2-2\sqrt{2}, \quad x_2=2+2\sqrt{2} \\ \\ -1< x \leq \dfrac{1}{4} \end{cases} \quad \vee \\ \\ & \vee \begin{cases} x_1=-2+\sqrt{10}, \quad x_2=-2-\sqrt{10} \\ \\ \dfrac{1}{4}< x \leq 1 \end{cases} \quad \vee \quad \begin{cases} x_{1,2} = 2 \\ \\ x > 1 \end{cases} \end{align*}Confrontando in ciascun sistema le soluzioni ottenute per l’equazione di secondo grado e la condizione per le {x} sottostante abbiamo le seguenti soluzioni per l’equazione con valori assoluti di partenza:
x_1=-2-\sqrt{2}, \qquad x_2 = 2-2\sqrt{2}, \qquad x_3=2Infatti ad esempio nel primo sistema dobbiamo scartare la soluzione {x_2=-2+\sqrt{2}} in quanto non rispetta la condizione {x \leq -1}. Infatti abbiamo {-2+\sqrt{2}\approx -0,586 > -1}. Procedendo in modo del tutto simile negli altri sistemi è stato possibile individuare le soluzioni accettabili per l’equazione di partenza, scartando le soluzioni estranee.
Conclusioni
Per quanto riguarda come risolvere le equazioni con valore assoluto è tutto. Per chi desidera allenarsi ulteriormente è disponibile la scheda di esercizi correlata. Ricordiamo l’importanza di aver ben presente la definizione di valore assoluto data nella precedente lezione, in modo da saper risolvere le equazioni con valore assoluto non soltanto per schemi meccanici ma anche in modo ragionato.
Un saluto a tutti e buon proseguimento con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
