Equazioni irrazionali

 - 

Equazioni (superiori)

Le equazioni irrazionali sono particolari equazioni ove l’incognita compare almeno una volta sotto il simbolo di radice. Per capire come risolvere tali equazioni occorre avere presenti le proprietà dei radicali. In ogni caso nella lezione presenteremo tutti i principali metodi risolutivi per le equazioni irrazionali.

L’idea per risolvere le equazioni irrazionali è quella di ricondurle ad equazioni algebriche che già sappiamo risolvere. In altre parole, ciò che dobbiamo fare è eliminare i simboli di radice, in modo da ricondurci ad un’equazione non irrazionale. Ma l’equazione che otterremo non sempre sarà equivalente all’equazione di partenza, e spesso dovrà infatti essere accompagnata da opportune condizioni. In particolare, come vedremo tra un istante dovremo distinguere tra equazioni ove compaiono radicali con indice dispari ed equazioni ove invece sono presenti radicali con indice pari.

Ma vediamo subito come risolvere le equazioni irrazionali nei vari casi.

Come risolvere le equazioni irrazionali

Primo caso: equazioni irrazionali con indice dispari

Consideriamo equazioni irrazionali elementari del tipo:

\sqrt[n]{f(x)}=a, \qquad a \in \mathbb{R}, \qquad n \: \text{dispari}

Per risolvere equazioni di questo tipo occorre rileggere in forma più generale i principi di equivalenza.

Ad esempio, il primo principio di equivalenza consiste nell’applicare a ciascun membro di un’equazione una stessa funzione {f(x)=x+q}, ove {q} è la stessa quantità che sommiamo a ciascun membro dell’equazione (quantità tale ovviamente da rispettare le ipotesi date a suo tempo). Allo stesso modo, il secondo principio di equivalenza consiste nell’applicare a ciascun membro dell’equazione la funzione {f(x)=x \cdot q}, ove {q} è la stessa quantità per la quale moltiplichiamo ciascun membro dell’equazione (ancora, una quantità tale da rispettare le ipotesi date a suo tempo).

Possiamo allora in generale affermare che, sotto le opportune ipotesi, se applichiamo ad entrambi i membri di un’equazione una stessa funzione otteniamo un’equazione equivalente a quella data.

Poiché, ricordiamo, per risolvere un’equazione irrazionale vogliamo eliminare i simboli di radice, nel nostro caso basterà applicare a ciascun membro dell’equazione {\sqrt[n]{f(x)}=a} la funzione {f(x)=x^n}. E ciò equivale in parole povere ad elevare alla {n} entrambi i membri dell’equazione data.

Consideriamo quindi ad esempio l’equazione (con radicando avente indice dispari {n=3}):

\sqrt[3]{x}=2

Per risolverla basterà elevare entrambi i membri al cubo (applicando così a ciascun membro la funzione {f(x)=x^3}) in modo da eliminare il simbolo di radice:

\left( \sqrt[3]{x}\right)^3=2^3 \quad \Rightarrow \quad x=8

Così abbiamo risolto l’equazione trovando quel numero la cui radice cubica è uguale a {2}.

Allo stesso modo sarà possibile risolvere equazioni del tipo:

\sqrt[n]{f(x)}=g(x), \qquad n \: \text{dispari}

Ad esempio data l’equazione:

\sqrt[3]{2-x^3}=2-x

il primo passo consiste nell’elevare al cubo entrambi i membri, in modo da liberarci dalla radice:

2-x^3=(2-x)^3

A questo punto occorrerà sviluppare il cubo di un binomio al secondo membro. Per comodità svolgiamo il calcolo separatamente:

\left(2-x\right)^3=8-3 \cdot 4 \cdot x+3 \cdot 2 \cdot x^2 -x^3

e quindi tornando all’equazione otteniamo:

6x^2-12x+6=0

ovvero:

x^2-2x+1=0

Da cui le soluzioni:

x_{1,2}=\dfrac{2 \pm \sqrt{(-2)^2- 4 \cdot 1 \cdot 1 }}{2 \cdot 1}=\dfrac{2\pm 0}{2}=1

Così in conclusione per l’equazione di partenza abbiamo la soluzione (con molteplicità due):

x_1 = 1

In modo del tutto simile, è possibile risolvere equazioni della forma:

\sqrt[n]{f(x)}=\sqrt[n]{g(x)}, \qquad n \: \text{dispari}

In tal caso infatti potremo ancora liberarci dei simboli di radice elevando alla {n} entrambi i membri.

Così, proviamo a risolvere l’equazione:

\sqrt[3]{3+x}=\sqrt[3]{2x^2-1}

Elevando entrambi i membri al cubo ci ritroviamo con l’equazione algebrica:

3+x=2x^2-1

Riscrivendola in forma normale:

2x^2-x-4=0

da cui le soluzioni:

x_{1,2}=\dfrac{1 \pm \sqrt{(-1)^2-4 \cdot 2 \cdot (-4)}}{2 \cdot 2}=\dfrac{1 \pm \sqrt{33}}{4}

L’equazione di partenza ammette dunque le soluzioni:

x_{1}=\dfrac{1+ \sqrt{33}}{4}; \qquad x_{2}= \dfrac{1 - \sqrt{33}}{4}

Secondo caso: equazioni irrazionali con indice pari

Come abbiamo visto le equazioni irrazionali aventi radicali con indice dispari non presentano particolari difficoltà. E’ infatti sufficiente sfruttare i principi di equivalenza in modo da ricondursi ad equazioni algebriche di risoluzione immediata.

Diverso è il caso invece delle equazioni irrazionali con indice pari.

Riprendiamo una delle proprietà fondamentali dei radicali:

\sqrt[n]{x^n}=|x|, \qquad n \: \text{pari}

Tale proprietà ci fa notare che se estraiamo la radice con indice pari di una quantità elevata a quello stesso indice, il risultato è definito soltanto come valore assoluto. Ciò è diretta conseguenza del fatto che se eleviamo ad esponente pari una quantità indifferentemente negativa o positiva, otteniamo sempre e comunque un risultato positivo. Detta in altri termini, l’operazione di elevazione a potenza con esponente pari non conserva necessariamente il segno della quantità di partenza.

Così entrambe le operazioni {(-2)^4} e {2^4} avranno come risultato la stessa quantità positiva {16}.

Consideriamo allora la seguente uguaglianza:

\sqrt{4}=-2

L’uguaglianza è evidentemente falsa. Ma proviamo ad elevare al quadrato entrambi i membri, in modo da liberarci del simbolo di radice esattamente come visto nei casi precedenti:

\left( \sqrt{4}\right)^2=(-2)^2 \quad \Rightarrow \quad 4=4

Attenzione: otteniamo in questo modo un’uguaglianza che è vera. Comprendiamo quindi che in presenza di radicali con indici pari dobbiamo prestare molta attenzione alle condizioni da porre nel risolvere le equazioni irrazionali.

Consideriamo la seguente equazione:

\sqrt{x-4}=3

Siamo in presenza di un’equazione irrazionale con indice del radicando pari. Infatti, al primo membro abbiamo una radice quadrata.

In questo caso non abbiamo problemi poiché la quantità al secondo membro è positiva. Così, se eleviamo tale quantità ad un esponente pari conserviamo il suo segno. Di conseguenza, possiamo tranquillamente elevare entrambi i membri dell’equazione di partenza all’esponente {2}, in modo da liberarci del simbolo di radice:

x-4=9

A questo punto ci siamo ricondotti ad una semplice equazione di primo grado che risolta fornisce:

x=13

e questa è anche la soluzione dell’equazione irrazionale di partenza.

Ma, consideriamo a questo punto la seguente equazione:

\sqrt{4-2x}+2=0

Riconduciamola alla forma {\sqrt[n]{f(x)}=a}:

\sqrt{4-2x}=-2

Come possiamo vedere ci ritroviamo con un’uguaglianza tra la quantità positiva al primo membro (necessariamente positiva poiché abbiamo una radice quadrata) e la quantità negativa al secondo membro. E’ dunque chiaro che l’equazione è impossibile, senza dover eseguire alcun calcolo. Tuttavia, proviamo ad elevare al quadrato entrambi i membri dell’equazione:

\left( \sqrt{4-2x}\right)^2=(-2)^2 \quad \Rightarrow \quad 4-2x=4

Come possiamo facilmente osservare ci ritroviamo con un’equazione di primo grado che risolta fornisce la soluzione:

-2x=4-4 \quad \Rightarrow \quad x=0

soluzione evidentemente non accettabile per l’equazione irrazionale di partenza.

Capiamo quindi che per evitare di ritrovarci con delle soluzioni estranee, ovvero delle “false soluzioni”, nel risolvere le equazioni irrazionali con indice dei radicali pari dobbiamo porre delle opportune condizioni.

Riprendiamo allora l’equazione:

\sqrt{4-2x}+2=0

che come detto diviene:

\sqrt{4-2x}=-2

Affinché l’equazione ammetta soluzioni deve valere la condizione di concordanza dei segni tra il primo membro e secondo membro. E dato che il primo membro è positivo, tale condizione si esprime con:

-2 \geq  0

disuguaglianza evidentemente falsa. Per cui ritroviamo conferma del fatto che l’equazione irrazionale data è impossibile, ovvero non ammette soluzioni.

Consideriamo ora un’equazione del tipo {\sqrt[n]{f(x)}=g(x)}, sempre con indice {n} pari:

\sqrt{3-x^2}=x-1

Imponiamo la condizione di concordanza dei segni tra i membri dell’equazione:

x-1 \geq 0

Per quanto riguarda il primo membro, abbiamo una radice quadrata (quindi con indice pari). Di conseguenza, l’argomento all’interno della radice non può essere negativo e quindi vale la condizione di realtà del radicale al primo membro:

3-x^2 \geq 0

Così potremo elevare al quadrato entrambi i membri dell’equazione data ma a patto di imporre contemporaneamente la condizione di concordanza dei segni e, almeno apparentemente, la condizione di realtà del radicale al primo membro:

\begin{cases} \left( \sqrt{3-x^2}\right)^2=(x-1)^2 \\ \\ x-1  \geq  0 \\ \\  3-x^2 \geq 0\end{cases}

e quindi, liberandoci del simbolo di radice:

\begin{cases}  3-x^2=(x-1)^2 \\ \\ x-1  \geq  0 \\ \\  3-x^2 \geq 0\end{cases}

Ora, attenzione. L’equazione a sistema ci dice che la quantità {3-x^2} è uguale ad una quantità positiva o al più nulla. Infatti, il secondo membro è il quadrato di un binomio, che può essere soltanto positivo o nullo. Di conseguenza, la condizione di realtà del radicale al primo membro dell’equazione di partenza è già compresa nell’equazione a sistema. Quindi, bisogna scartare la condizione di realtà del radicale e limitarci a considerare la sola condizione di concordanza dei segni:

\begin{cases}  3-x^2=(x-1)^2 \\ \\ x-1  \geq  0\end{cases}

Di conseguenza si tratta di mettere a sistema l’equazione che si ottiene elevando all’indice pari del radicale entrambi i membri dell’equazione di partenza insieme alla condizione di concordanza (secondo membro richiesto positivo).

Svolgendo i calcoli il sistema diviene:

\begin{cases}3-x^2=x^2-2x+1 \\ \\ x \geq  1\end{cases}

ovvero:

\begin{cases}2x^2-2x-2=0  \\ \\ x  \geq  1  \end{cases}

e quindi:

\begin{cases}x^2-x-1=0 \\ \\ x \geq 1 \end{cases}

Così in pratica si tratterà di risolvere l’equazione di secondo grado e verificare che le sue soluzioni rispettino la condizione {x \geq 1}. E soltanto le soluzioni che rispettano tale condizione saranno soluzioni dell’equazione irrazionale di partenza.

Risolviamo allora l’equazione di secondo grado:

x_{1,2} = \dfrac{1 \pm \sqrt{(-1)^2-4 \cdot 1 \cdot (-1)}}{2 \cdot 1}=\dfrac{1 \pm \sqrt{5}}{2}

Così per l’equazione di secondo grado all’interno del sistema abbiamo le due soluzioni:

x_{1}=\dfrac{1+ \sqrt{5}}{2}; \qquad x_2=\dfrac{1-\sqrt{5}}{2}

Ora, attenzione. Ciascuna soluzione ottenuta deve essere confrontata con la condizione di concordanza dei segni, ovvero in questo caso con la condizione {x \geq 1}. Concludiamo così che la soluzione {x_2} non è accettabile poiché non è maggiore o uguale a {1}. Quindi in conclusione per l’equazione irrazionale di partenza abbiamo la sola soluzione:

x_1=\dfrac{1+\sqrt{5}}{2}

Consideriamo ora la seguente equazione:

\sqrt{4x+x^2}-\sqrt{-2+x}=0

Portiamo un radicale al secondo membro, in modo da ricondurci alla forma {\sqrt[n]{f(x)}=\sqrt[n]{g(x)}}:

\sqrt{4x+x^2}=\sqrt{-2+x}

Osserviamo che in questo caso non dobbiamo porre alcuna condizione di concordanza. Infatti, il segno di entrambe le quantità a primo e a secondo membro è positivo (si tratta infatti in entrambi i casi di radicali con indice pari).

Per quanto riguarda le condizioni di realtà dei radicali, invece, rispetto al caso precedente il discorso ora è differente. Infatti, se eleviamo entrambi i membri dell’equazione data al quadrato, non otteniamo alcuna condizione sul segno dei radicandi.

Pertanto, ci ritroviamo a dover imporre le condizioni di realtà dei radicali, ovvero:

4x+x^2 \geq 0 

e:

-2+x \geq 0

Così le condizioni di realtà dei radicali necessarie per l’equazione in esame corrispondono al sistema:

\begin{cases}4x+x^2 \geq 0 \\ \\ -2+x \geq 0  \end{cases}

ovvero:

\begin{cases} x(4+x) \geq 0 \\ \\ -2+x \geq 0 \end{cases}

Per quanto riguarda la prima condizione a sistema, si tratta di studiare il segno del prodotto {x (4 + x)}:

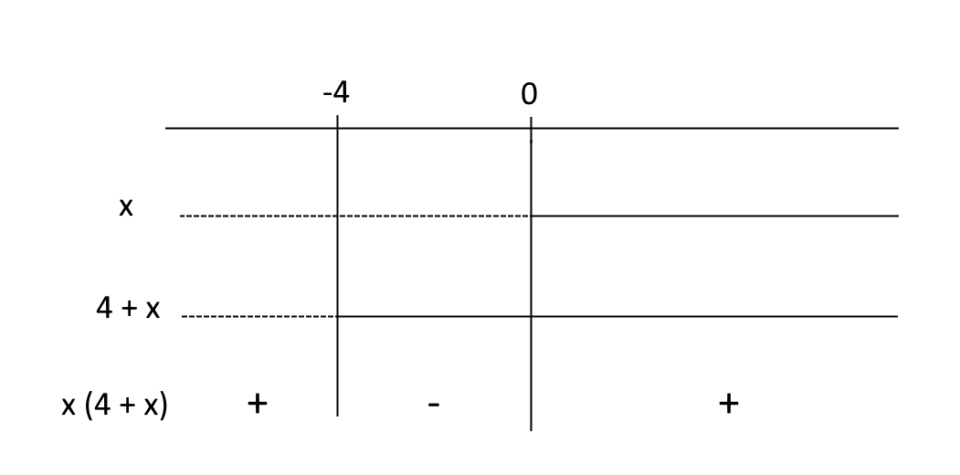
Da ciò otteniamo la condizione {x \leq -4 \: \vee \: x \geq 0}.

Per la seconda condizione otteniamo invece {x \geq 2}. Così, intersecando le due condizioni appena scritte abbiamo:

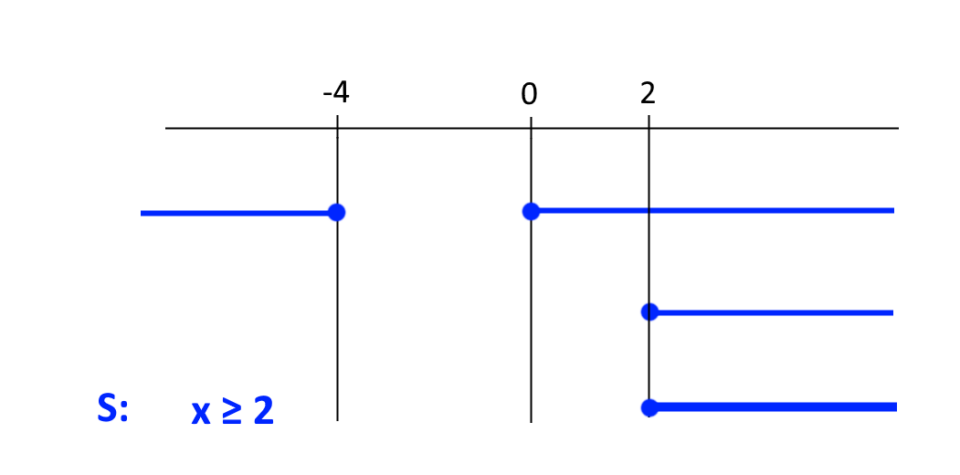
Di conseguenza, per risolvere l’equazione irrazionale di partenza {\sqrt{4x+x^2}=\sqrt{-2+x}} basterà risolvere il seguente sistema:

\begin{cases}\left(\sqrt{4x+x^2} \right)^2=\left(\sqrt{-2+x}\right)^2 \\ \\ x \geq 2 \end{cases}

Sviluppando i calcoli:

\begin{cases}4x+x^2=-2+x \\ \\  x \geq 2 \end{cases}

Risolviamo l’equazione di secondo grado accettando le sole soluzioni che rispettano la condizione {x \geq 2}. Abbiamo:

4x+x^2+2-x=0 \quad \Rightarrow \quad x^2+3x+2=0

da cui otteniamo le soluzioni:

x_{1,2} = \dfrac{-3 \pm \sqrt{3^2-4 \cdot 1 \cdot 2}}{2 \cdot 1}=\dfrac{-3 \pm 1}{2}=\begin{cases}-1  \\ \\ -2 \end{cases}

Ora attenzione: nessuna delle due soluzioni rispetta la condizione {x \geq 2}. Di conseguenza l’equazione irrazionale di partenza è impossibile, ovvero non ammette alcuna soluzione.

Equazioni con due radicali e un termine noto o con più di due radicali

Concludiamo questa lezione considerando ulteriori forme di equazioni irrazionali, per le quali comunque valgono le indicazioni sin qui illustrate. Consideriamo l’equazione:

\sqrt{1+2x}+\sqrt{5+x}=3

Osserviamo che il primo membro è sempre positivo poiché somma di termini sempre positivi (radicali con indice pari). Anche il secondo membro è sempre positivo poiché abbiamo un solo termine dato da una costante positiva. Di conseguenza non dobbiamo imporre alcuna condizione di concordanza dei segni.

Possiamo allora elevare entrambi i membri dell’equazione al quadrato, imponendo però contemporaneamente le condizioni di realtà dei radicali. Infatti, come sappiamo, l’argomento di un radicale con indice pari deve essere necessariamente non negativo. Abbiamo:

\begin{cases}\left(\sqrt{1+2x}+\sqrt{5+x}\right)^2=3^2  \\ \\ 1 + 2x \geq 0 \\ \\ 5+x \geq 0 \end{cases}

Concentriamoci per ora sulle sole condizioni di realtà in modo da ricavare per comodità un’unica condizione ad esse corrispondente :

\begin{cases}1 + 2x \geq 0 \\ \\ 5 + x \geq 0  \end{cases} \quad \Rightarrow \quad \begin{cases}x \geq -\dfrac{1}{2} \\ \\ x \geq -5 \end{cases} \quad \Rightarrow \quad  x \geq -\dfrac{1}{2}

A questo punto possiamo sostituire il sistema scritto all’inizio con il seguente, che contiene al posto delle due condizioni di realtà di partenza la sola condizione appena scritta:

\begin{cases}\left(\sqrt{1+2x}+\sqrt{5+x}\right)^2=3^2  \\ \\x \geq -\dfrac{1}{2}\end{cases}

Si tratterà ora di risolvere l’equazione presente nel sistema, accettando le sole soluzioni che rispettano la condizione {x \geq -\dfrac{1}{2}}.

Osserviamo che al primo membro dell’equazione abbiamo il quadrato di un binomio, ovvero un’espressione del tipo {(A+B)^2} con {A=\sqrt{1+2x}} e {B=\sqrt{5+x}}. Così in merito al solo primo membro avremo:

\begin{align*} & \left(\sqrt{1+2x}+\sqrt{5+x}\right)^2=(A+B)^2=A^2+2AB+B^2= \\ \\ & =\underbrace{1+2x}_{A^2}+\underbrace{2 \cdot \sqrt{1+2x} \cdot \sqrt{5+x}}_{2AB}+\underbrace{5+x}_{B^2}=\end{align*}

Per proseguire i passaggi occorre ricordare la regola del prodotto tra radicali con lo stesso indice. Abbiamo quindi:

\begin{align*} & =1+2x+2\sqrt{(1+2x)(5+x)}+5+x= \\ \\ & =3x+2\sqrt{(1+2x)(5+x)}+6= \\ \\ & =3x+2\sqrt{5+11x+2x^2}+6\end{align*} 

Così riprendendo l’ultimo sistema scritto abbiamo:

\begin{cases}3x+2\sqrt{5+11x+2x^2}+6=9  \\ \\x \geq -\dfrac{1}{2}\end{cases}

ovvero:

\begin{cases} 2\sqrt{2x^2+11x+5}=3(1-x) \\ \\ x \geq -\dfrac{1}{2}\end{cases}

Si tratterà a questo punto di risolvere l’equazione razionale a sistema, accettando le sole soluzioni che soddisfano la condizione {x \geq -\dfrac{1}{2}}.

Riscriviamo l’equazione irrazionale a sistema nella forma {\sqrt[n]{f(x)} = g(x)}:

\sqrt{2x^2+11x+5}=\dfrac{3}{2}(1-x)

Come visto negli esempi precedenti, l’equazione avrà a sua volta delle soluzioni tali da soddisfare il sistema:

\begin{cases} \overbrace{\left( \sqrt{2x^2+11x+5}\right)^2 =\dfrac{9}{4}(1-x)^2 }^{\text{entrambi i membri elevati al quadrato}}\\ \\ \underbrace{\dfrac{3}{2}(1-x) \geq 0}_{\text{condizione di concordanza}} \end{cases}

Sviluppando i calcoli:

\begin{cases} 2x^2+11x+5=\dfrac{9}{4}x^2-\dfrac{9}{2}x+\dfrac{9}{4} \\ \\ x \leq 1\end{cases}

ovvero:

\begin{cases}\dfrac{1}{4}x^2 -\dfrac{31}{2}x-\dfrac{11}{4}=0 \\ \\ x \leq 1\end{cases}

Risolviamo l’equazione a sistema accettando le sole soluzioni tali da soddisfare la condizione {x \leq 1}. Abbiamo:

\begin{align*} & x_{1,2}=\dfrac{\dfrac{31}{2} \pm \sqrt{\left( -\dfrac{31}{2}\right)^2-4 \cdot \dfrac{1}{4} \cdot \left( -\dfrac{11}{4}\right)}}{2 \cdot \dfrac{1}{4}}=\\ \\ & =\dfrac{\dfrac{31}{2}\pm \sqrt{\dfrac{961}{4}+\dfrac{11}{4}}}{\dfrac{1}{2}} =\dfrac{\dfrac{31}{2}\pm \dfrac{1}{2}\sqrt{972}}{\dfrac{1}{2}}=31 \pm 18\sqrt{3}\end{align*}

La soluzione che possiamo accettare è soltanto {x=31-18\sqrt{3}}, poiché è l’unica che soddisfa la condizione {x \leq 1}.

Ora, attenzione. Per poter stabilire se la soluzione ottenuta è anche soluzione dell’equazione irrazionale di partenza, dobbiamo tornare indietro al primo sistema scritto e considerare la relativa condizione. In particolare, in esso abbiamo la condizione:

x \geq -\dfrac{1}{2}

la quale è soddisfatta dalla soluzione {x=31-18\sqrt{3}}, che è quindi in conclusione anche soluzione dell’equazione irrazionale di partenza.

Prima di salutarci, vediamo un ultimo esempio relativo al caso di equazioni irrazionali con più di due radicali. Risolviamo insieme la seguente equazione irrazionale:

\sqrt{4-x}-\sqrt{2-x}-\sqrt{1-x}=0

In questi casi è opportuno ricondurre l’equazione alla forma:

\sqrt{f_1(x)}+\sqrt{f_2(x)}=\sqrt{f_3(x)}

e quindi nel nostro caso scriveremo:

\sqrt{4-x}-\sqrt{2-x}=\sqrt{1-x}

Osserviamo che sia il primo membro, sia il secondo membro saranno positivi per ogni valore della {x}. Infatti, anche la differenza al primo membro sarà sempre positiva poiché il radicando {4-x} è una quantità sempre maggiore del radicando {2-x}, ed inoltre i due radicali hanno entrambi indice {2}. Di conseguenza, non è necessaria alcuna condizione di concordanza dei segni.

Imponiamo invece le condizioni di realtà dei radicali:

\begin{cases} 4-x \geq 0 \\ \\ 2-x \geq 0 \\ \\ 1-x \geq 0 \end{cases}

ovvero:

\begin{cases} x \leq 4 \\ \\ x \leq 2 \\ \\ x \leq 1 \end{cases}

Il sistema è soddisfatto da tutti i valori tali da rispettare la condizione:

x \leq 1

Ora, sotto la condizione appena scritta è possibile elevare al quadrato entrambi i membri dell’equazione irrazionale data:

\begin{cases} \left(\sqrt{4-x}-\sqrt{2-x} \right)^2=\left( \sqrt{1-x} \right)^2  \\ \\ x \leq 1\end{cases}

Al primo membro dell’equazione a sistema riconosciamo il quadrato di un binomio. Infatti, ci ritroviamo a dover calcolare l’espressione {(A-B)^2} con {A = \sqrt{4-x}} e {B=\sqrt{2-x}}. Per cui relativamente al solo primo membro dell’equazione abbiamo:

\begin{align*} &\left(\underbrace{\sqrt{4-x}}_{A}-\underbrace{\sqrt{2-x}}_{B} \right)^2=(A-B)^2=A^2-2AB+B^2 = \\ \\ & =\left( \sqrt{4-x}\right)^2-2 \cdot \sqrt{4-x} \cdot \sqrt{2-x}+\left(\sqrt{ 2-x}\right)^2=\\ \\ & =4-x-2 \sqrt{(4-x)(2-x)}+2-x=\\ \\ & =4-x-2\sqrt{8-4x-2x+x^2}+2-x = \\ \\ & =-2x+6-2\sqrt{x^2-6x+8}\end{align*}

Di conseguenza tornando al sistema abbiamo:

\begin{cases} -2x+6-2\sqrt{x^2-6x+8}=1-x \\ \\ x \leq 1\end{cases}

ovvero:

\begin{cases}-x+5=2\sqrt{x^2-6x+8}  \\ \\   x \leq 1\end{cases}

Risolviamo a questo punto la prima equazione irrazionale a sistema, accettando poi soltanto le soluzioni che rispettano la condizione {x \leq 1}. Abbiamo:

(-x+5)^2=\left( 2\sqrt{x^2-6x+8}\right)^2

e quindi, tenendo conto per il secondo membro che {\left( 2\sqrt{x^2-6x+8}\right)^2=2^2 \cdot \left( \sqrt{x^2-6x+8}\right)^2} (vedi proprietà delle potenze), per l’equazione possiamo scrivere:

\begin{align*} & x^2-10x+25=4(x^2-6x+8) \\ \\ & x^2-10x+25=4x^2-24x+32 \\ \\ & 3x^2-14x+7=0  \end{align*}

Otteniamo per l’equazione di secondo grado le soluzioni:

x_{1,2} = \dfrac{14 \pm \sqrt{196-4 \cdot 3 \cdot 7}}{2 \cdot 3}=\dfrac{14 \pm \sqrt{112}}{6}=\dfrac{14 \pm 4 \sqrt{7}}{6}=\dfrac{7 \pm 2\sqrt{7}}{3}

Ora, attenzione. Ricordiamo che possiamo accettare per l’equazione irrazionale di partenza soltanto le soluzioni che rispettano la condizione {x \leq 1}.

Fra le due soluzioni ottenute, l’unica che rispetta tale condizione è {x=\dfrac{7-2\sqrt{7}}{3}}. E soltanto questa è soluzione dell’equazione irrazionale di partenza.

Quindi in conclusione l’equazione irrazionale data ammette la soluzione:

x=\dfrac{7-2\sqrt{7}}{3}

Conclusioni

Qui termina la lezione sulle equazioni irrazionali, nei due casi di indici dei radicali pari o dispari. Osserviamo che i metodi risolutivi appena visti nel caso delle equazioni irrazionali con due radicali più termine noto o con più di due radicali sono validi anche nel caso di indici dispari. In quest’ultimo caso ovviamente non dovremmo imporre alcuna condizione di realtà (come abbiamo visto all’inizio di questa lezione).

Per quanto riguarda le equazioni irrazionali è tutto. Per allenarvi ulteriormente non perdetevi la scheda di esercizi correlata (vedi link in basso). Buon proseguimento con SìMatematica!