Proponiamo in questa scheda degli esercizi sui sistemi lineari (o sistemi di equazioni di primo grado) pensati per gli studenti delle scuole superiori. Gli esercizi qui proposti accompagnano la lezione intensiva sui sistemi lineari, nella quale vengono spiegati i metodi di sostituzione, di riduzione e la regola di Cramer. Nella presente esercitazione comprenderemo anche esercizi sul metodo del confronto, per il quale rimandiamo per ulteriori approfondimenti alla lezione teorica dedicata.
Potrete qui trovare in particolare degli esercizi sui sistemi lineari che utilizzano tutti i metodi. Per ciascun esercizio mostreremo lo svolgimento con il metodo risolutivo più adatto, ma in alcuni casi utilizzeremo in via alternativa anche più metodi risolutivi per lo stesso sistema lineare. Sarà così possibile effettuare un confronto tra i metodi risolutivi, in modo da poter acquisire l’abilità di saper scegliere il metodo più adatto in base alla forma nella quale si presenta il sistema da risolvere.
Nella prima parte dell’esercitazione vedremo esercizi relativi a sistemi lineari di sole due equazioni in due incognite. Nella seconda parte passeremo a sistemi lineari di tre equazioni in tre incognite.
Vediamo allora subito questa serie di esercizi sui sistemi lineari (sistemi di equazioni di primo grado), nel caso di due equazioni in due incognite e di tre equazioni in tre incognite, svolti con i vari metodi risolutivi.
Esercizi sui sistemi lineari (sistemi di equazioni di primo grado), con i vari metodi
Prima di passare agli svolgimenti degli esercizi sui sistemi lineari, ricordiamo che un sistema lineare è un sistema di equazioni di primo grado, ovvero un insieme di due o più equazioni che devono essere soddisfatte contemporaneamente. Così risolvere un sistema significa cercare gli eventuali valori che sostituiti alle incognite verificano tutte le equazioni presenti nel sistema stesso.
Un sistema lineare di due equazioni in due incognite in forma normale si scrive come:
\begin{cases} a_1x+b_1y=k_1 \\ \\ a_2x+b_2y=k_2\end{cases}ove {a_1, \: b_1, \: a_2, \: b_2 } sono i coefficienti delle incognite, mentre {k_1, \: k_2} sono i termini noti. E’ praticamente sempre obbligatorio ricondurre un sistema alla forma normale prima di apprestarsi a risolverlo (se naturalmente non è già in tale forma). E per fare ciò è sufficiente trasportare opportunamente i termini in ciascuna equazione.
Ora, ricordiamo che due sistemi si dicono equivalenti se le equazioni del primo sistema sono equivalenti alle rispettive equazioni del secondo sistema. Così se sostituiamo un’equazione del sistema con una nuova equazione ad essa equivalente otteniamo un sistema equivalente a quello di partenza. E su questo principio si basano i metodi risolutivi di riduzione e del confronto. Anche il metodo di sostituzione si fonda su questo ragionamento, ma in esso ritroviamo anche il principio di sostituzione. Nei metodi di riduzione e del confronto ritroviamo invece un’applicazione del primo e del secondo principio di equivalenza delle equazioni.
Un ultimo metodo che infine analizzeremo in questa scheda è dato dal metodo di Cramer. Si tratta del metodo più meccanico per risolvere i sistemi lineari, grazie al quale è possibile determinare l’eventuale soluzione del sistema mediante delle opportune formule, calcolando particolari quantità note come determinanti.
Ma vediamo subito come utilizzare i metodi risolutivi menzionati con degli esercizi sui sistemi lineari svolti passo dopo passo, con ciascun metodo. Ci limitiamo per ora ad esercizi su sistemi con due equazioni in due incognite, rimandando per gli esercizi sui sistemi di tre equazioni in tre incognite alla parte successiva di questa scheda.
Importante. In questa scheda supporremo di avere a che fare esclusivamente con sistemi lineari determinati.
Esercizi sui sistemi lineari di due equazioni in due incognite
Esercizio 1
Risolviamo il seguente sistema:
\begin{cases} x+y=1 \\ \\ x-y=3\end{cases}Il sistema è già in forma normale per cui non dobbiamo trasportare alcun termine.
Risolviamo il sistema con il metodo di sostituzione. Per fare questo, dobbiamo ricavare un’espressione per l’incognita in funzione dell’altra da una delle due equazioni, e quindi sostituire tale espressione ad una incognita nell’altra equazione. In tal modo otteniamo un’equazione in una sola incognita che possiamo risolvere. E una volta ricavato il valore per un’incognita, basterà sostituirlo nell’altra equazione in modo da ricavare il valore della rimanente incognita. A questo punto il sistema sarà risolto poiché è nota la coppia di valori {(x, \: y)} soluzione del sistema.
Per iniziare possiamo scegliere a piacere un’equazione tra le due presenti, e quindi esplicitare un’incognita. Ovviamente, è bene operare la scelta in modo da rendere i calcoli i più semplici possibili. Così è ad esempio una buona idea ricavare la {x} dalla prima equazione, mentre è sicuramente non consigliabile anche se corretto ricavare la {y} dalla seconda equazione. Operando questa scelta infatti ci ritroveremmo a dover ragionare con i segni (la {y} è negativa). Non si tratta certo di calcoli difficoltosi, ma onde evitare errori sempre meglio scegliere le strade più dirette ove possibile.
Ricaviamo allora la {x} dalla prima equazione (attenzione a cambiare sempre il segno dei termini che trasportiamo da un membro all’altro di un’equazione):
\begin{cases} x=1-y \\ \\ x-y=3\end{cases}Ma a questo punto la prima equazione ci dice che {x} è esprimibile come {1-y}. E la quantità {x} compare anche nella seconda equazione. E’ allora intuibile che possiamo sostituire alla quantità {x} nella seconda equazione la quantità {1-y}. In questo modo ci ritroviamo come seconda equazione del sistema un’equazione nella sola incognita y. Abbiamo:
\begin{cases} x=1 - y \\ \\ \underbrace{(1-y)}_{x}-y=3\end{cases}Ora sommiamo i termini simili nella seconda equazione, quindi ricaviamo da essa il valore dell’incognita {y}. Possiamo farlo poiché effettivamente si tratta soltanto di risolvere un’equazione di primo grado.
\begin{cases} x=1 - y \\ \\ -2y=3-1 \quad \rightarrow \quad y=-1\end{cases}Abbiamo così ricavato il valore dell’incognita {y}. Ora non resta che ricavare il valore dell’incognita {x}, e per fare questo basta sostituire il valore di {y} nella seconda equazione. Abbiamo:
\begin{cases} x = 1- (-1)=2 \\ \\ y=-1\end{cases}In questo modo abbiamo anche trovato il valore dell’incognita {x}. Il sistema è così risolto e la sua soluzione è data dalla coppia di valori {(x, \: y)}:
(2, \: -1)
Esercizio 1-bis (metodo di riduzione)
Vediamo ora come risolvere il sistema precedente ma con il metodo di riduzione. Riportiamo il sistema nella sua forma di partenza:
\begin{cases} x+y = 1 \\ \\ x-y=3\end{cases}Il metodo di riduzione è un’applicazione del primo principio di equivalenza. Osserviamo anzitutto che la seconda equazione afferma che la quantità {x-y} e la quantità {3} sono tra loro uguali. Così, possiamo rappresentare entrambe le quantità ad esempio con la lettera {Q}.
Ora, consideriamo ad esempio la prima equazione. Per il primo principio di equivalenza possiamo senz’altro scrivere:
x+y+Q=1+Q
Nulla ci impedisce di sostituire a {Q} la quantità {x-y} al primo membro, e la quantità {3} al secondo membro. Infatti, per la seconda equazione tali quantità sono uguali. Abbiamo:
x+y+x-y=1+3
In questo modo abbiamo in pratica sommato membro a membro la prima equazione e la seconda equazione. E attenzione, poiché abbiamo utilizzato il primo principio di equivalenza, la nuova equazione così ottenuta è equivalente alla prima equazione a sistema (e lo è anche alla seconda). Di conseguenza, possiamo sostituire la nuova equazione ottenuta alla prima equazione a sistema, ottenendo un sistema equivalente a quello di partenza. Abbiamo così:
\begin{cases} x+y+x-y=1+3 \\ \\ x-y=3\end{cases}Sommando i termini simili nella prima equazione otteniamo:
\begin{cases} x+\cancel{y}+x-\cancel{y}=1+3 \quad \rightarrow \quad 2x=4 \quad \rightarrow \quad x=2 \\ \\ x-y=3 \end{cases}e quindi:
\begin{cases} x=2 \\ \\ x-y=3 \end{cases}Abbiamo in questo modo ricavato il valore dell’incognita {x}. E’ fondamentale osservare che nel sommare le due equazioni membro a membro tra loro abbiamo eliminato l’incognita {y}. Infatti nell’eseguire la somma i termini in {y} si sono cancellati tra loro.
Nell’applicare il metodo di riduzione dobbiamo scegliere due equazioni che contengano termini in una data incognita aventi lo stesso coefficiente oppure coefficienti tra loro opposti, o comunque dobbiamo ricondurci a tale circostanza (vedi esercizio successivo). In questo modo la nuova equazione risulterà priva di tale incognita, e sostituendo la nuova equazione ottenuta nel sistema avremo ridotto il numero delle incognite rispetto all’equazione presente in precedenza.
Ora è conveniente sostituire il valore della {x} appena ottenuto nella seconda equazione, ma per esercizio ripetiamo ancora l’utilizzo del metodo di riduzione. Sottraiamo allora la seconda equazione alla prima, membro a membro, e sostituiamo la nuova equazione ottenuta alla seconda equazione. Abbiamo:
\begin{cases} x=2 \\ \\ x-(x-y)=2-3 \quad \rightarrow \quad \cancel{x}-\cancel{x}+y=-1 \quad \rightarrow \quad y=-1\end{cases}E quindi:
\begin{cases} x= 2 \\ \\ y = -1\end{cases}Ritroviamo così per le incognite gli stessi valori ottenuti con il metodo di sostituzione.
Il metodo di riduzione risulta un po’ più macchinoso rispetto al metodo di sostituzione per sistemi molto semplici. Ma per sistemi meno semplici e con più equazioni il metodo di riduzione risulta in realtà generalmente quello più pratico da usare.
Esercizio 2
Proseguiamo gli esercizi sui sistemi lineari con il seguente:
\begin{cases} x+2y=8 \\ \\ 3x-4y=4 \end{cases}Utilizziamo in questo caso il metodo di riduzione. Ma prima dobbiamo fare in modo che nelle due equazioni compaiano dei termini in una data incognita aventi lo stesso coefficiente. Come possiamo vedere tale condizione non è al momento verificata. Infatti nella prima equazione la {x} ha coefficiente {1} mentre nella seconda equazione ha coefficiente {3}. Allo stesso modo, la {y} ha coefficiente {2} nella prima equazione ma coefficiente {-4} nella seconda.
Proviamo allora a moltiplicare tutti i termini della prima equazione per {2}. Ciò corrisponde ad applicare alla prima equazione il secondo principio di equivalenza. Abbiamo:
\begin{cases} 2x+4y=16 \\ \\ 3x-4y=4 \end{cases}Ma a questo punto compaiono nella prima e nella seconda equazione dei termini in {y} che sono almeno uguali tra loro in valore assoluto (ovvero, differiscono tra loro solo per il segno). Ma allora se sommiamo membro a membro le due equazioni tra loro, i termini in {y} si cancelleranno. Sommiamo allora membro a membro la prima e la seconda equazione, quindi sostituiamo la nuova equazione ottenuta ad esempio alla seconda equazione a sistema. Abbiamo:
\begin{cases}2x+4y=16 \\ \\ 2x+4y+3x-4y=16+4 \end{cases}Sommando i termini simili nella seconda equazione otteniamo:
\begin{cases}2x+4y=16 \\ \\ 2x+\cancel{4y}+3x-\cancel{4y}=16+4 \quad \rightarrow \quad 5x=20 \quad \rightarrow \quad x=4\end{cases}A questo punto conviene semplicemente sostituire il valore della {x} appena ottenuto nella prima equazione, in modo da ricavare il valore dell’incognita {y}:
\begin{cases} 2x+4y= 16 \quad \rightarrow \quad y=\dfrac{16-2\cdot 4}{4}=\dfrac{8}{4}=2\\ \\ x = 4\end{cases}Il sistema è così risolto ed ammette come soluzione la coppia di valori:
(4, \: 2)
Esercizio 3
Vediamo ora come svolgere gli esercizi sui sistemi lineari di due equazioni in due incognite utilizzando il metodo del confronto. Risolviamo il seguente sistema:
\begin{cases} 2x-6y= -14 \\ \\ 2x-8y=-4\end{cases}Il metodo del confronto si basa sull’idea di ricavare l’espressione per una stessa incognita da entrambe le equazioni del sistema (siamo nel caso di sistemi di due equazioni in due incognite).
Osserviamo che in entrambe le equazioni abbiamo lo stesso termine {2x}. Possiamo allora ottenere un’espressione per la stessa quantità {2x} da entrambe le equazioni:
\begin{cases} 2x=\boxed{-14+6y} \\ \\ 2x = \boxed{-4+8y}\end{cases}Osserviamo che non dobbiamo necessariamente isolare l’incognita {x}. Se anche otteniamo espressioni per una stessa quantità multipla di {x} (in questo caso {2x}), è la stessa cosa.
A questo punto possiamo ottenere una nuova equazione equivalente a quelle presenti uguagliando tra loro le espressioni evidenziate nei riquadri. Fatto ciò possiamo sostituire la nuova equazione ottenuta ad esempio alla prima equazione presente nel sistema. Così abbiamo:
\begin{cases}\boxed{-14+6y}=\boxed{-4+8y} \\ \\ 2x=-4+8y \end{cases}Ci ritroviamo con la prima equazione del sistema che ora contiene una sola incognita. Possiamo quindi ricavare il valore di {y} dalla prima equazione:
\begin{cases}-14+6y=-4+8y \quad \rightarrow \quad 2y=-10 \quad \rightarrow \quad y=-5 \\ \\ 2x=-4+8y \end{cases}Ora possiamo ricavare il valore della rimanente incognita {x} sostituendo nella seconda equazione il valore appena trovato per la {y}:
\begin{cases} y=-5 \\ \\ 2x=-4+8 \cdot (-5) \quad \rightarrow \quad x=\dfrac{-4-40}{2}=-22\end{cases}Così in conclusione il sistema ammette come soluzione la coppia:
(-22, \: -5)
Vediamo ora come risolvere questo stesso esercizio utilizzando il metodo di Cramer.
Esercizio 3 bis (metodo di Cramer)
Riscriviamo il sistema lineare dell’esercizio precedente nella forma di partenza:
\begin{cases} 2x-6y= -14 \\ \\ 2x-8y=-4\end{cases}Prima di applicare il metodo di Cramer, il controllo preliminare da fare è che il sistema sia in forma normale. Inoltre, è assolutamente consigliabile indicare esplicitamente anche gli eventuali coefficienti zero delle incognite. Vedremo meglio questo aspetto in un successivo esercizio.
In questo caso il sistema è già in forma normale ed inoltre compaiono tutte le incognite nel sistema, per cui non abbiamo problemi.
La matrice dei coefficienti è una tabella che contiene i coefficienti delle incognite così come compaiono nel sistema. Nel caso del sistema in esame la matrice dei coefficienti è:
\begin{bmatrix}2 & -6 \\ 2 & -8 \end{bmatrix}A partire dalla matrice dei coefficienti occorre calcolare il determinante della matrice dei coefficienti, il determinante {D_x} e il determinante {D_y}. Una volta note queste quantità sarà possibile ricavare i valori delle incognite del sistema con delle semplici formule.
Il determinante della matrice dei coefficienti si calcola come segue (come visto nella lezione teorica):
D=\det \begin{bmatrix} 2 & -6 \\ 2 & - 8\end{bmatrix}=2 \cdot (-8) - 2 \cdot (-6) = -16+12=-4Ricordiamo che si tratta di calcolare la differenza tra il prodotto degli elementi che si trovano nella diagonale discendente da sinistra verso destra e il prodotto degli elementi che si trovano nella diagonale ascendente da sinistra verso destra.
Il determinante {D_x} è il determinante della matrice che si ottiene a partire dalla matrice dei coefficienti, sostituendo alla colonna dei coefficienti dell’incognita {x} la colonna dei termini noti del sistema.
Nel nostro caso la colonna dei termini noti del sistema è:
\begin{matrix}-14 \\ \\ -4 \end{matrix}sostituendo la colonna dei termini noti alla colonna dei coefficienti delle incognite {x} nella matrice dei coefficienti otteniamo la seguente matrice:
\begin{bmatrix} \textbf{-14} & -6 \\ \textbf{-4} & -8\end{bmatrix}il cui determinante è:
D_x=\det \begin{bmatrix} -14 & -6 \\ -4 & -8\end{bmatrix}= -14 \cdot (-8)-(-4) \cdot (-6)=112-24=88Infine, sostituendo la colonna dei termini noti del sistema alla colonna dei termini in {y} nella matrice dei coefficienti otteniamo la seguente matrice:
\begin{bmatrix} 2 & \textbf{-14} \\ 2 & \textbf{-4}\end{bmatrix}il cui determinante è:
D_y = \det \begin{bmatrix} 2 & -14 \\ 2 & -4\end{bmatrix} = 2 \cdot (-4) - 2 \cdot (-14) = -8+28=20Ora abbiamo tutti gli ingredienti per calcolare i valori delle incognite del sistema. Ricordiamo che le formule del metodo di Cramer per ricavare i valori delle incognite di un sistema di due equazioni in due incognite sono:
x= \dfrac{D_x}{D}; \qquad y=\dfrac{D_y}{D}Sostituendo i valori dei determinati precedentemente calcolati otteniamo per il sistema in esame:
x = \dfrac{D_x}{D}=\dfrac{88}{-4}=-22; \qquad y=\dfrac{D_y}{D}=\dfrac{20}{-4}=-5Così il sistema ha per soluzione la coppia:
(-22, \: -5)
Esercizio 4
Proseguiamo gli esercizi sui sistemi lineari di due equazioni in due incognite con il seguente sistema lineare:
\begin{cases}4(x-3)-(4y-1)= x \\ \\ 5-2x=4(x-3)-3y \end{cases}Osserviamo prima di tutto che il sistema non è in forma normale. Per cui dovremo anzitutto calcolare i prodotti, trasportare i termini ove necessario e quindi sommare tra loro i termini simili. Cominciamo calcolando i prodotti:
\begin{cases} 4x-12-4y+1 = x \\ \\ 5-2x=4x-12-3y\end{cases}Ora trasportiamo opportunamente i termini in modo da avere soltanto quantità numeriche al secondo membro e soltanto quantità letterali al primo membro:
\begin{cases} 4x-4y-x=12-1 \\ \\ -2x-4x+3y=-12-5\end{cases}A questo punto sommiamo tra loro i termini simili:
\begin{cases} 3x-4y=11 \\ \\ -6x+3y=-17\end{cases}Ora il sistema si presenta in forma normale e possiamo convenientemente utilizzare uno dei metodi risolutivi sin qui visti. Proviamo a risolvere il sistema con il metodo di riduzione.
Anzitutto, moltiplichiamo per {2} tutti i termini della prima equazione, in modo da avere nelle equazioni dei termini in {x} uguali tra loro in modulo. Abbiamo:
\begin{cases} 6x-8y=22 \\ \\ -6x+3y=-17\end{cases}Ora ricaviamo una nuova equazione sommando tra loro membro a membro le due equazioni. Sostituiamo la nuova equazione così ottenuta ad esempio alla prima equazione. Si ha:
\begin{cases} 6x-8y+(-6x+3y)=22+(-17) \\ \\ -6x+3y=-17\end{cases}Sommando i termini simili nella prima equazione:
\begin{cases}\cancel{6x}-8y-\cancel{6x}+3y=22-17 \quad \rightarrow \quad -5y=5 \quad \rightarrow \quad y=-1\\ \\ -6x+3y=-17\end{cases}Abbiamo così ricavato il valore dell’incognita {y}. Ora non resta che ricavare per sostituzione l’incognita {x} dalla seconda equazione:
\small \begin{cases} y=-1 \\ \\ -6x+3y=-17 \:\:\rightarrow \: -6x=-17-3y \:\rightarrow \:x=\dfrac{17+3y}{6}=\dfrac{17+3 \cdot (-1)}{6}=\dfrac{7}{3}\end{cases}Così in conclusione il sistema ammette come soluzione la coppia { \left( x, \: y\right)} di valori:
\left( \dfrac{7}{3}, \: -1\right)Esercizio 5
Veniamo all’ultimo di questi esercizi sui sistemi lineari di due equazioni in due incognite di questa scheda, per poi passare ai sistemi lineari di tre equazioni in tre incognite.
Risolviamo insieme il seguente sistema:
\begin{cases} 4(1-y)=x-5(2+y)+12 \\ \\ 5-2(4-x)=6-(y-1)\end{cases}Prima di tutto riconduciamo il sistema alla forma normale. Calcoliamo i prodotti:
\begin{cases} 4-4y=x-10-5y+12 \\ \\ 5 - 8 + 2x=6-y+1 \end{cases}Trasportiamo i termini in modo da avere soltanto quantità numeriche al secondo membro e soltanto quantità letterali al primo membro di ciascuna equazione:
\begin{cases} -4y-x+5y=-10+12-4 \\ \\ 2x+y=6+1-5+8\end{cases}Sommiamo i termini simili:
\begin{cases} y-x=-2 \\ \\ 2x+y=10\end{cases}Risolviamo il sistema utilizzando ad esempio il metodo del confronto. Appare invitante utilizzare questo metodo poiché in entrambe le equazioni figura lo stesso termine {y}.
Esplicitiamo allora la {y} in entrambe le equazioni:
\begin{cases} y=-2+x \\ \\ y=10-2x\end{cases}Ora uguagliamo i due secondi membri delle equazioni appena scritte, e sostituiamo la nuova equazione così ottenuta ad esempio alla prima equazione del sistema. Abbiamo:
\begin{cases} -2+x=10-2x \\ \\ y=10-2x\end{cases}Ricaviamo infine la {x} dalla prima equazione, e quindi sostituiamo il valore ottenuto nella seconda equazione:
\begin{cases} 3x=12 \quad \rightarrow \quad x = \dfrac{12}{3}=4 \\ \\ y=10-2 \cdot (4) = 2\end{cases}Così in conclusione il sistema ammette per soluzione la coppia:
\left( 4, \: 2\right)
Esercizi sui sistemi lineari di tre equazioni in tre incognite
Cominciamo ora a vedere come risolvere i sistemi lineari di tre equazioni in tre incognite. Ma prima di entrare nel merito dei metodi risolutivi, è opportuno evidenziare il salto concettuale che dobbiamo fare nel passaggio dai sistemi lineari di due equazioni in due incognite a quelli di tre equazioni in tre incognite.
Sottolineiamo che i discorsi che qui faremo riguardano soltanto i metodi di sostituzione, riduzione e del confronto. Utilizzando invece il metodo di Cramer l’unica cosa che cambia nei sistemi di tre equazioni in tre incognite è il più difficoltoso calcolo dei determinanti. Per il resto, le formule per il calcolo dei valori delle incognite non sono certamente più difficili di quelle relative al caso dei sistemi di due equazioni in due incognite.
Ora, in un sistema lineare di due equazioni in due incognite, ridotto in forma normale, è sufficiente sostituire un’equazione del sistema a nostra scelta con un’altra ad essa equivalente. A tal punto, sarà subito possibile ricavare un valore di una delle incognite. E infine, basterà sostituire il valore ottenuto dell’incognita nell’altra equazione, ricavando la rimanente incognita. Tutto qui.
Nel caso dei sistemi lineari di tre equazioni in tre incognite, invece, il discorso non è così diretto. Tuttavia, i ragionamenti da seguire sono ancora tutti basati sui principi di equivalenza delle equazioni e sulla definizione di sistemi equivalenti.
Consideriamo un sistema di tre equazioni in tre incognite che, nel caso più generale, presenti tutte e tre le incognite con coefficienti diversi da zero in ciascuna equazione.
All’inizio basterà ancora sostituire un’equazione del sistema a nostra scelta con un’altra ad essa equivalente. Ma a tal punto, dovremo prestare attenzione.
Ora, la prima cosa da chiederci è: la nuova equazione che abbiamo scritto nel sistema, quali incognite ha? Ad esempio, supponiamo che la nuova equazione inserita nel sistema sia nelle incognite {x} e {z}.
In questo caso, nel ricavare un’ulteriore nuova equazione da utilizzare nel sistema, dovremo prestare attenzione che questa contenga le due stesse incognite x e z. Infatti, soltanto in questo modo ci ritroveremo poi nel sistema con due equazioni nelle due stesse incognite {x} e {z}. E questo è importante poiché, ricordiamo, nel risolvere i sistemi di tre equazioni in tre incognite dobbiamo ricondurci, almeno temporaneamente, ad un sistema di due equazioni in due incognite.
Una volta che abbiamo nel sistema due equazioni ove compaiono le due stesse incognite, possiamo escludere la rimanente equazione e quindi ragionare come se fossimo di fronte ad un sistema di due equazioni in due incognite. In tal modo sarà possibile ricavare i valori delle due incognite presenti nelle due equazioni.
Soltanto a tal punto riprenderemo l’equazione che avevamo messo da parte e sostituiremo in essa i valori sinora ricavati per le incognite. E in conclusione sarà così possibile ricavare agevolmente il valore della rimanente incognita.
Abbiamo così presentato in modo discorsivo una importante traccia comune per poter risolvere i sistemi lineari di tre equazioni in tre incognite utilizzando i metodi di sostituzione, di riduzione e del confronto. E utilizzando un metodo oppure un altro, cambierà soltanto il modo con il quale ricaviamo le nuove equazioni da utilizzare nel sistema, ma il procedimento da seguire è concettualmente quello sin qui illustrato.
Per il metodo di Cramer, invece, come già detto l’unica difficoltà nel passaggio ai sistemi di tre equazioni in tre incognite è data dal calcolo dei determinanti. Ma di questo ci occuperemo in un esercizio alla fine di questa scheda.
Esercizio 6
Risolviamo insieme il seguente sistema lineare di tre equazioni in tre incognite:
\begin{cases} x-2y+2z=-4 \\ \\ x+y-8z = 8 \\ \\ -x-4y+16z=-20\end{cases}Osserviamo anzitutto che il sistema è già in forma normale. Proviamo a risolverlo utilizzando ad esempio il metodo di riduzione, che probabilmente è almeno in linea generale il più pratico per i sistemi di tre equazioni in tre incognite.
Le prime due equazioni contengono lo stesso termine {x}. Per cui se sottraiamo membro a membro la seconda equazione alla prima i termini {x} si cancellano tra loro ed otteniamo una nuova equazione nelle sole due incognite {y} e {z}. Cominciamo a scrivere la nuova equazione, sostituendola al posto esclusivamente di una delle due equazioni utilizzate per ricavarla (ad esempio, scegliamo la prima equazione). Abbiamo:
\begin{cases} x-2y+2z-(x+y-8z)=-4-8 \\ \\ x+y-8z = 8 \\ \\ -x-4y+16z=-20\end{cases}Attenzione. Ricordiamo che è possibile inserire una nuova equazione in un sistema soltanto al posto di una delle due equazioni utilizzate per ricavarla. Se avessimo quindi inserito in questo caso la nuova equazione al posto della terza equazione del sistema avremmo commesso un errore. E come risultato non saremmo riusciti ad andare avanti nella risoluzione del sistema stesso.
Sommando i termini simili nella prima equazione otteniamo:
\small \begin{cases} \cancel{x}-2y+2z-\cancel{x}-y+8z=-4-8 \: \: \rightarrow \:\: -3y+10z=-12\\ \\ x+y-8z = 8 \\ \\ -x-4y+16z=-20\end{cases}e quindi:
\small \begin{cases} -3y+10z=-12\\ \\ x+y-8z = 8 \\ \\ -x-4y+16z=-20\end{cases}E’ ora fondamentale osservare che la prima equazione nel sistema si presenta nelle sole incognite {y} e {z}. Dobbiamo allora procedere sostituendo una delle rimanenti equazioni del sistema con una nuova equazione anch’essa nelle sole incognite y e z.
Utilizziamo ancora il metodo di riduzione sommando tra loro la seconda e la terza equazione. In questo modo effettivamente i termini {x} e {-x} si cancellano tra loro, e ci ritroviamo con un’equazione nelle sole incognite {y} e {z}. Sostituiamo la nuova equazione che così si ottiene ad esempio alla seconda equazione del sistema (in alternativa avremmo anche potuto sostituire la terza equazione, ma, attenzione, non la prima). Abbiamo:
\small \begin{cases} -3y+10z=-12\\ \\ x+y-8z+(-x-4y+16z)=8+(-20) \\ \\ -x-4y+16z=-20\end{cases}Sommiamo i termini simili nella seconda equazione:
\small \begin{cases} -3y+9z=-12\\ \\\cancel{x}+y-8z-\cancel{x}-4y+16z=8-20 \: \: \rightarrow \: \: -3y+8z=-12 \\ \\ -x-4y+16z=-20\end{cases}e quindi:
\small \begin{cases} -3y+9z=-12\\ \\\ -3y+8z=-12 \\ \\ -x-4y+16z=-20\end{cases}A questo punto ci ritroviamo con due equazioni che contengono le due sole stesse incognite {y} e {z}. Possiamo quindi mettere da parte la rimanente equazione e ragionare come se avessimo un sistema di due equazioni in due incognite:
\small \begin{cases} -3y+9z=-12\\ \\\ -3y+8z=-12 \\ \\ \dots \end{cases}Utilizziamo ancora il metodo di riduzione. Sommiamo le due equazioni tra loro membro a membro e sostituiamo la nuova equazione che così si ottiene ad esempio al posto della prima equazione:
\begin{cases} 17z=0 \quad \rightarrow \quad z= 0 \\ \\ -3y+8z=-12 \\ \\ \dots \end{cases}Ora sostituiamo il valore appena ricavato per {z} nella seconda equazione, in modo da ricavare la {y}:
\begin{cases} z= 0 \\ \\ -3y+8 \cdot 0=-12 \quad \rightarrow \quad y=4\\ \\ \dots \end{cases}A questo punto riprendiamo l’equazione messa da parte e sostituiamo in essa i valori delle incognite sin qui ricavate. In questo modo otteniamo il valore dell’ultima incognita rimasta, ovvero la {x}:
\small \begin{cases} z= 0 \\ \\ y = 4 \\ \\ -x-4y+16z=-20 \: \: \rightarrow \: \: x & =20-4 \cdot 4+16 \cdot 0 = 4\end{cases}Così in conclusione il sistema ha come soluzione la terna {(x, \: y, \: z)} seguente:
\left( 4, \: 4, \: 0\right)
Esercizio 7
Risolvere il seguente sistema lineare:
\begin{cases} x-y= 1 \\ \\ x+2z=0 \\ \\ y-z=-1\end{cases}Il sistema è già in forma normale. Osserviamo tuttavia che se vogliamo risolverlo utilizzando ad esempio la regola di Cramer, dobbiamo anche riportare esplicitamente le incognite aventi coefficiente 0 in ciascuna equazione. Non è invece necessaria tale operazione se intendiamo utilizzare altri metodi.
Proviamo con il metodo di Cramer. Cominciamo riportando esplicitamente anche le incognite aventi coefficiente zero:
\begin{cases} x-y+0z= 1 \\ \\ x+0y+2z=0 \\ \\ 0x+y-z=-1\end{cases}Avendo riscritto il sistema in questa forma, è ora immediato scrivere la matrice dei coefficienti riducendo al minimo la possibilità di errori:
\det \begin{bmatrix} 1 & -1 & 0 \\ 1 & 0 & 2 \\ 0 & 1 & -1 \end{bmatrix}A questo punto calcoliamo i determinanti. Cominciamo dal determinante della matrice dei coefficienti:
D=\det \begin{bmatrix} 1 & -1 & 0 \\ 1 & 0 & 2 \\ 0 & 1 & -1 \end{bmatrix}=Per effettuare il calcolo utilizziamo la regola di Sarrus. Cominciamo riportando le prime due colonne della matrice dei coefficienti a seguire la matrice stessa:
\begin{bmatrix} 1 & -1 & 0 \\ 1 & 0 & 2 \\ 0 & 1 & -1 \end{bmatrix} \: \:\begin{matrix} 1 & - 1 \\ 1 & 0 \\ 0 & 1 \end{matrix}Consideriamo le diagonali discendenti (in rosso) e quelle ascendenti (in blu).
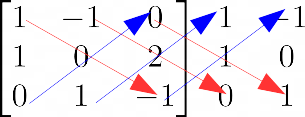
Ora scriviamo il determinante della matrice dei coefficienti sommando tra loro i prodotti degli elementi che si trovano in ciascuna diagonale discendente (in rosso), e quindi sottraendo uno a uno i prodotti corrispondenti a ciascuna diagonale ascendente (in blu). Abbiamo:
\begin{align*} & D=\det \begin{bmatrix} 1 & -1 & 0 \\ 1 & 0 & 2 \\ 0 & 1 & -1 \end{bmatrix}= \\ \\ & =1 \cdot 0 \cdot (-1) + (-1) \cdot 2 \cdot 0 + 0 \cdot 1 \cdot 1 - 0 \cdot 0 \cdot 0 - 1 \cdot 2 \cdot 1 - (-1) \cdot 1 \cdot -1=\\ \\ & =0+0+0-0-2-1=-3\end{align*}Con la stessa regola è possibile calcolare i determinanti {D_x, \: D_y, \: D_z}, ovvero, ricordiamo, i determinanti delle matrici che si ottengono sostituendo, nella matrice dei coefficienti, alla colonna dei coefficienti dell’incognita x, oppure y oppure z la colonna dei termini noti del sistema.
Ricordiamo che la colonna dei termini noti del sistema è formata dai termini noti nell’ordine in cui compaiono nel sistema. Nel nostro caso la colonna dei termini noti del sistema è:
\begin{matrix} 1 \\ 0 \\ -1\end{matrix}Così abbiamo:
\small \begin{align*} & D_x = \det \begin{bmatrix} \textbf{1} & -1 & 0 \\ \textbf{0} & 0 & 2 \\ \textbf{-1} & 1 & -1\end{bmatrix}= \\ \\ & =1 \cdot 0 \cdot (-1)+(-1)\cdot2 \cdot (-1)+0\cdot0\cdot1 -(-1)\cdot0\cdot0-1 \cdot 2 \cdot 1 -(-1)\cdot 0 \cdot (-1)=\\ \\ & =0+2+0-0-2-0=0\end{align*}e con calcoli del tutto simili, che per brevità omettiamo:
D_y = \det \begin{bmatrix} 1 & \textbf{1} & 0 \\ 1 & \textbf{0} & 2 \\ 0 & \textbf{-1} & -1\end{bmatrix}= 3; \qquad D_z=\det \begin{bmatrix} 1 & -1 & \textbf{1} \\ 1 & 0 & \textbf{0} \\ 0 & 1 & \textbf{-1}\end{bmatrix}=0Ora che abbiamo tutti i determinanti, grazie alle formule del metodo di Cramer possiamo ricavare i valori delle incognite {x, \: y, \: z}:
\begin{align*} & x=\dfrac{D_x}{D}=\dfrac{0}{-3}=0; \qquad y=\dfrac{D_y}{D}=\dfrac{3}{-3}=-1; \\ \\ &z=\dfrac{D_z}{D}= \dfrac{0}{-3}=0 \end{align*}Così in conclusione il sistema ha per soluzione la terna:
(0, \: -1, \: 0)
Esercizio 7 bis
Proseguiamo ancora questi esercizi sui sistemi lineari riprendendo il sistema dell’esercizio precedente:
\begin{cases} x-y= 1 \\ \\ x+2z=0 \\ \\ y-z=-1\end{cases}La presenza di poche incognite in ciascuna equazione con coefficienti quasi tutti unitari suggerisce di utilizzare convenientemente il metodo del confronto. Cominciamo esplicitando la {x} nelle prime due equazioni:
\begin{cases} x= 1 + y \\ \\ x=-2z \\ \\ y-z=-1\end{cases}Uguagliamo tra loro le due espressioni ottenute per {x}, e sostituiamo la nuova equazione così ottenuta ad esempio alla prima equazione. Abbiamo:
\begin{cases} 1+y=-2z \\ \\ x = -2z \\ \\ y-z=-1\end{cases}A questo punto escludiamo la seconda equazione in modo da ritrovarci con due equazioni nelle stesse incognite {y} e {z}:
\begin{cases} 1+y=-2z \\ \\ \dots \\ \\ y-z=-1\end{cases}Ragioniamo quindi come se avessimo un sistema di due equazioni in due equazioni. Applichiamo ancora il metodo del confronto, ricavando un’espressione per l’incognita {y} da entrambe le equazioni:
\begin{cases}y=\boxed{-2z-1} \\ \\ \dots \\ \\ y=\boxed{-1+z} \end{cases}Ora uguagliando tra loro le due espressioni nell’incognita {z} otteniamo un’equazione nella sola incognita {z}, alla quale possiamo ad esempio sostituire la prima equazione a sistema. Abbiamo:
\begin{cases} -2z-1=-1+z \\ \\ \dots \\ \\ y=-1+z\end{cases}La prima equazione è nella sola incognita {z}, e da essa riusciamo facilmente a ricavare il valore di tale incognita. Di conseguenza, per sostituzione possiamo ricavare anche il valore dell’incognita {y}.
\begin{cases} z = 0 \\ \\ \dots \\ \\ y=-1+z \quad \rightarrow \quad y=-1\end{cases}Ora non resta che recuperare la seconda equazione in modo da ricavare il valore della {x}:
\begin{cases} z = 0 \\ \\ x = -2z=0 \\ \\ y=-1+z \quad \rightarrow \quad y=-1\end{cases}Ritroviamo così i valori già calcolati con il metodo precedente.
Esercizio 8
Concludiamo questa serie di esercizi sui sistemi lineari con il seguente sistema di tre equazioni in tre incognite:
\begin{cases} x+y=z+4 \\ \\ x-y+2z=-5 \\ \\ 3x-1=-(2z+y)\end{cases}Anzitutto eliminiamo le parentesi tonde al secondo membro della terza equazione. Ovviamente, attenzione ai segni:
\begin{cases} x+y=z+4 \\ \\ x-y+2z=-5 \\ \\ 3x-1=-2z-y \end{cases}Ora trasportiamo opportunamente i termini in modo da ricondurre il sistema alla forma normale:
\begin{cases} x+y-z=4 \\ \\ x-y+2z=-5 \\ \\ 3x+y+2z= 1\end{cases}Importante. Ricordiamo che nello scrivere un sistema in forma normale dobbiamo anche prestare attenzione all’ordine nel quale si presentano le incognite al primo membro, che deve essere alfabetico.
Risolviamo il sistema utilizzando il metodo di Cramer. In questo modo rivedremo insieme come applicare la regola di Sarrus per il calcolo dei determinanti delle matrici tre per tre.
Cominciamo scrivendo la matrice dei coefficienti delle incognite del sistema:
\begin{bmatrix} 1 & 1 & -1 \\ 1 & -1 & 2 \\ 3 & 1 & 2\end{bmatrix}Calcoliamo a questo punto il determinante {D} della matrice dei coefficienti. Per fare questo, conviene prima di tutto ricopiare le prime due colonne della matrice dei coefficienti scrivendole di seguito alla matrice stessa:
\begin{bmatrix} 1 & 1 & -1 \\ 1 & -1 & 2 \\ 3 & 1 & 2\end{bmatrix} \: \: \begin{matrix} 1 & 1 \\ 1 & -1 \\ 3 & 1\end{matrix}Poi, occorre individuare le diagonali discendenti (che indicheremo in rosso) e le diagonali ascendenti (che indicheremo in blu):
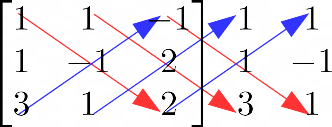
Ora sommiamo tra loro tutti i prodotti degli elementi che si trovano nelle diagonali discendenti (in rosso), e sottraiamo ciascun prodotto che si trova in ogni diagonale ascendente (in blu). Ciò che otteniamo è il valore del determinante {D} della matrice dei coefficienti. Così:
\small \begin{align*} & D=\det \begin{bmatrix} 1 & 1 & -1 \\ 1 & -1 & 2 \\ 3 & 1 & 2\end{bmatrix}= \\ \\ & =1 \cdot (-1) \cdot 2 + 1 \cdot 2 \cdot 3 + (-1) \cdot 1 \cdot 1 -3 \cdot (-1)\cdot(-1)-1 \cdot 2 \cdot 1 - 2 \cdot 1 \cdot 1 = \\ \\ & =-2+6-1-3-2-2=-4 \end{align*}Ora dobbiamo ricavare i determinanti {D_x, \: D_y, \: D_z}.
Il determinante {D_x} è il determinante della matrice che si ottiene sostituendo alla prima colonna della matrice dei coefficienti la colonna dei termini noti del sistema. Per calcolare {D_x} dovremo quindi considerare la seguente matrice:
\begin{bmatrix} \textbf{4} & 1 & -1 \\ \textbf{-5} & -1 & 2 \\ \textbf{1} & 1 & 2\end{bmatrix}Infatti, a partire dalla matrice dei coefficienti, abbiamo sostituito alla colonna dei coefficienti dei termini nell’incognita {x} (la prima colonna), la colonna dei termini noti, formata dai termini noti delle equazioni all’interno del sistema nell’ordine in cui si presentano nel sistema stesso. Per maggior chiarezza riportiamo di nuovo a seguire il sistema da risolvere evidenziando la colonna dei termini noti:
\begin{cases} x+y-z=\textbf{4} \\ \\ x-y+2z=\textbf{-5} \\ \\ 3x+y+2z= \textbf{1}\end{cases}Per calcolare il determinante della matrice così ottenuta utilizziamo di nuovo la regola di Sarrus. Così il calcolo segue le stesse regole di quello visto per la matrice dei coefficienti.
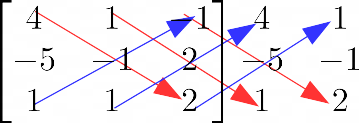
\small \begin{align*} & D_x = \det \begin{bmatrix} \textbf{{4}} & 1 & -1 \\ \textbf{{-5}} & -1 & 2 \\ \textbf{{1}} & 1 & 2\end{bmatrix} = \\ \\ & =4 \cdot (-1) \cdot 2 + 1 \cdot 2 \cdot 1 + (-1) \cdot (-5) \cdot 1 - 1 \cdot (-1) \cdot (-1)-1 \cdot 2 \cdot 4 - 2 \cdot (-5) \cdot 1 = \\ \\ & = -8+2+5-1-8+10=0 \end{align*}Procedendo in modo del tutto simile otteniamo per i determinanti {D_y} e {D_z}.
Il determinante {D_y} è il determinante della matrice dei coefficienti ove però sostituiamo alla colonna delle incognite {y} (seconda colonna) la colonna dei termini noti del sistema:
\small \begin{align*} & D_y=\det \begin{bmatrix} 1 & \textbf{4} & -1 \\ 1 & \textbf{-5} & 2 \\ 3 & \textbf{1} & 2\end{bmatrix} =\\ \\ & =1 \cdot(-5) \cdot 2 + 4 \cdot 2 \cdot 3 +(-1)\cdot1\cdot 1 - 3 \cdot (-5)\cdot(-1)-1\cdot2\cdot1 -2 \cdot 1 \cdot 4 = \\ \\ & = -10+24-1-15-2-8=-12 \end{align*}Similmente, {D_z} è il determinante della matrice dei coefficienti nella quale però sostituiamo all’ultima colonna la colonna dei coefficienti del sistema:
\small \begin{align*} & D_z= \det \begin{bmatrix} 1 & 1 & \textbf{4} \\ 1 & -1 & \textbf{-5} \\ 3 & 1 & \textbf{1} \end{bmatrix}=\\ \\ & =1 \cdot (-1) \cdot 1 + 1 \cdot (-5) \cdot 3 + 4 \cdot 1 \cdot 1 - 3 \cdot (-1) \cdot 4 - 1 \cdot (-5) \cdot 1 - 1\cdot 1 \cdot 1 =\\ \\ & =-1-15+4+12+5-1=4 \end{align*}Ora non resta che calcolare i valori delle incognite {x, \: y, \: z} utilizzando le formule del metodo di Cramer per i sistemi di tre equazioni in tre incognite:
\begin{align*} & x=\dfrac{D_x}{D}=\dfrac{0}{-4}=0; \qquad y=\dfrac{D_y}{D}=\dfrac{-12}{-4}=3; \\ \\ & z= \dfrac{D_z}{D}=\dfrac{4}{-4}=-1\end{align*}E siamo così arrivati al risultato finale anche per questo ultimo esercizio di questa scheda di esercizi sui sistemi lineari. In conclusione il sistema ha come soluzione la terna {(x, \: y, \: z)}:
\left( 0, \: 3, \: -1\right)
Conclusioni
Qui termina questa serie di esercizi sui sistemi lineari con i vari metodi (metodo di sostituzione, metodo di riduzione, metodo del confronto, regola di Cramer). Abbiamo in particolare visto come risolvere i sistemi lineari (o sistemi di equazioni di primo grado), sia nel caso di due equazioni in due incognite, sia nel caso di tre equazioni in tre incognite. Ed avendo visto in azione tutti e quattro i metodi risolutivi, possiamo fare qualche considerazione prima di salutarci.
Il metodo di sostituzione è quello concettualmente più semplice, anche se può diventare macchinoso, soprattutto nel caso dei sistemi lineari di tre equazioni in tre incognite.
Il metodo di riduzione è un po’ meno intuitivo rispetto al metodo di sostituzione, tuttavia consente di risolvere in maniera più fluida i sistemi, specialmente nel caso dei sistemi lineari dalle tre equazioni in su. In questi casi infatti il metodo di sostituzione può anche comportare dei calcoli algebrici decisamente pesanti.
Per quanto riguarda il metodo del confronto, come sappiamo questo è uno stretto parente del metodo di riduzione ed è conveniente soltanto in alcuni casi particolari. E ciò dipende dalla forma delle equazioni presenti all’interno del sistema lineare da risolvere.
Infine, il metodo di Cramer è il più meccanico di tutti e tre. Non richiede particolari considerazioni da fare sul piano concettuale né tantomeno accorgimenti speciali nel caso di sistemi di tre equazioni in tre incognite. E questo effettivamente è un grande vantaggio rispetto agli altri tre metodi. Tuttavia, lo svantaggio legato all’utilizzo del metodo di Cramer per lo svolgimento degli esercizi sui sistemi lineari è dato dal fatto di dover calcolare, nel caso di tre equazioni in tre incognite, i determinanti di matrici di tre righe per tre colonne. Per fare questo abbiamo visto la regola di Sarrus che, seppur non certo complicata sul piano concettuale, richiede comunque pazienza e particolare attenzione. E non solo, se utilizziamo il metodo di Cramer dobbiamo stare particolarmente attenti a riscrivere correttamente il sistema di partenza, se necessario, in forma normale.
In conclusione, la scelta del metodo più adatto per risolvere un dato sistema lineare è vostra, a meno che il metodo da usare non venga richiesto espressamente dal testo dell’esercizio. Noi di SìMatematica riteniamo utile consigliarvi il metodo di riduzione, poiché è quello che di solito si rivela il più efficiente per i sistemi lineari. E inoltre, è anche possibile risolvere i sistemi lineari in maniera mista, ovvero utilizzando dapprima il metodo di riduzione, e poi quello di sostituzione. Del resto abbiamo utilizzato quest’ultimo approccio in molti esercizi.
Un saluto a tutti voi e buon proseguimento con SìMatematica! 🙂
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
