In questa scheda vediamo una serie di esercizi sul prodotto di radicali con indici diversi. L’obiettivo è quello di mettere ulteriormente in pratica quanto visto nella lezione sul prodotto di radicali con indici diversi. Vedremo inoltre anche il caso del quoziente tra radicali con indici diversi, che comunque è riconducibile al prodotto.
Ci occuperemo in particolare sia del caso di radicali con radicandi numerici, sia del caso di radicali con radicandi letterali (radicandi che dipendono da almeno una variabile). Nel secondo caso, vedremo le discussione che dovremo effettuare.
Partiamo allora subito con gli esercizi sul prodotto di radicali con indici diversi.
Esercizi svolti e commentati sul prodotto e quoziente di radicali con indici diversi
Prima parte: radicandi numerici
Esercizio 1
Calcolare il seguente prodotto:
\sqrt[4]{\dfrac{3}{2}} \cdot \sqrt{\dfrac{2}{3}}Prima di tutto dobbiamo portare i radicali allo stesso indice. Per fare questo basta sfruttare la proprietà invariantiva dei radicali:
\begin{align*} &\sqrt[4]{\dfrac{3}{2}} \cdot \sqrt{\dfrac{2}{3}} = \sqrt[4]{\dfrac{3}{2}} \cdot \sqrt[2 \cdot 2]{\left( \dfrac{2}{3}\right)^2}= \sqrt[4]{\dfrac{3}{2}} \cdot \sqrt[4]{\dfrac{4}{9}} = \end{align*}A questo punto basta applicare la regola del prodotto di radicali con lo stesso indice:
=\sqrt[4]{\dfrac{3}{2} \cdot \dfrac{4}{9}}=\sqrt[4]{\dfrac{2}{3}}Siamo così arrivati al risultato finale. Possiamo in conclusione scrivere:
\sqrt[4]{\dfrac{3}{2}} \cdot \sqrt{\dfrac{2}{3}}=\sqrt[4]{\dfrac{2}{3}}Esercizio 2
Vediamo come calcolare il seguente prodotto fra radicali con indici differenti:
\sqrt[3]{\dfrac{21}{4}} \cdot \sqrt{\dfrac{6}{7}}Come nel precedente esercizio, prima di tutto riduciamo i radicali allo stesso indice. Inoltre, scomponiamo in fattori le quantità nei radicandi:
\begin{align*} &\sqrt[3]{\dfrac{21}{4}} \cdot \sqrt{\dfrac{6}{7}}=\sqrt[3 \cdot 2]{\dfrac{21^2}{4^2}} \cdot \sqrt[2 \cdot 3]{\dfrac{6^3}{7^3}}=\sqrt[6]{\dfrac{(7 \cdot 3)^2}{(2^2)^2} } \cdot \sqrt[6]{ \dfrac{(3 \cdot 2)^3}{7^3}}= \\ \\ & = \sqrt[6]{\dfrac{7^2 \cdot 3^2 }{2^4} } \cdot \sqrt[6]{\dfrac{3^3 \cdot 2^3}{7^3}} = \end{align*}A questo punto applichiamo la regola del prodotto tra radicali con lo stesso indice, effettuando delle semplificazioni grazie alle proprietà delle potenze:
\begin{align*} & = \sqrt[6]{\dfrac{7^2 \cdot 3^2 }{2^4} \cdot\dfrac{3^3 \cdot 2^3}{7^3}} =\sqrt[6]{\dfrac{\cancel{7^2} \cdot 3^5 \cdot \cancel{2^3}}{2^{\cancel{4}} \cdot 7^{\cancel{3}}}}= \sqrt[6]{\dfrac{3^5}{2 \cdot 7}}=\sqrt[6]{\dfrac{243}{14}} \end{align*}Esercizio 3
Passiamo al seguente quoziente tra radicali con indici differenti. Calcolare:
\dfrac{\sqrt[3]{10}}{\sqrt{10}}La regola consiste nel ridurre i radicali allo stesso indice, e quindi scrivere come quoziente un radicale avente per indice il comune indice e per radicando il rapporto tra i radicandi dei radicali ridotti allo stesso indice.
Abbiamo:
\dfrac{\sqrt[3]{10}}{\sqrt{10}}=\dfrac{\sqrt[3 \cdot 2]{10^2}}{\sqrt[2 \cdot 3]{10^3}}= \dfrac{\sqrt[6]{10^2}}{\sqrt[6]{10^3}}=\sqrt[6]{\dfrac{10^2}{10^3}}=\sqrt[6]{\dfrac{1}{10}}=\dfrac{1}{\sqrt[6]{10}}Osserviamo che avremmo potuto anche ragionare con il prodotto fra radicali:
\begin{align*} & \dfrac{\sqrt[3]{10}}{\sqrt{10}}=\sqrt[3]{10} \cdot \dfrac{1}{\sqrt{10}}=\sqrt[6]{10^2} \cdot \dfrac{1}{\sqrt[6]{10^3}}=\sqrt[6]{10^2 \cdot \dfrac{1}{10^3}}= \\ \\ & =\sqrt[6]{\dfrac{1}{10}}=\dfrac{1}{\sqrt[6]{10}} \end{align*}Parte seconda: radicandi letterali
Nel caso degli esercizi sul prodotto di radicali con indici differenti aventi radicandi letterali (radicandi dipendenti da almeno una variabile), dovremo:
- determinare il campo di esistenza del prodotto dei radicali a partire dai campi di esistenza dei singoli radicali nel prodotto;
- determinare il segno del prodotto in base al segno dei singoli fattori di partenza.
Dovremo quindi stabilire per quali valori della variabile (o delle variabili) esiste il prodotto dei radicali e come cambia il segno del prodotto stesso proprio in base al valore della variabile (o delle variabili).
Esercizio 4
Calcolare:
\sqrt{x-1} \cdot \sqrt[3]{(x+1)^2}Determiniamo anzitutto i campi di esistenza dei due radicali. Il primo radicale ha indice pari ed è di conseguenza definito soltanto per i valori della {x} che rendono il radicando positivo o al più nullo:
x-1 \geq 0 \iff x \geq 1
Il secondo radicale è invece definito per ogni valore reale della {x}. Infatti l’indice del radicale è dispari e il radicale è un polinomio (i polinomi così come li abbiamo definiti esistono per tutti i valori reali della variabile).
Di conseguenza il prodotto dei radicali dati esiste nell’insieme dato dall’intersezione tra i due campi di esistenza, e quindi per {x \geq 1}.
Ora, per quanto riguarda il segno del prodotto, osserviamo che il primo radicale è sempre positivo (si tratta infatti di un radicale con indice pari). Anche il secondo radicale è sempre positivo. Infatti, pur trattandosi di un radicale con indice dispari, il radicando è elevato al quadrato ed è quindi sempre positivo.
Così in conclusione il prodotto è sempre positivo e per la condizione di esistenza data possiamo scrivere, utilizzando le regole dei precedenti esercizi:
\begin{align*} &\sqrt{x-1} \cdot \sqrt[3]{(x+1)^2} = \sqrt[2 \cdot 3]{(x-1)^3} \cdot \sqrt[3 \cdot 2]{(x+1)^{2 \cdot 2 }}=\\ \\ & =\sqrt[6]{(x-1)^3} \cdot \sqrt[6]{(x+1)^4}=\sqrt[6]{(x-1)^3 \cdot (x+1)^4}= \\ \\ & =\sqrt[6]{(x-1)^3 \cdot (x+1)^3 \cdot(x+1)}= \sqrt[6]{[(x-1)(x+1)]^3 \cdot (x+1) } = \\ \\ & =\sqrt[6]{(x^2-1)^3 \cdot (x+1)}, \qquad x \geq 1 \end{align*}Esercizio 5
Calcolare:
\sqrt{3+x} \cdot \sqrt[4]{4-x}Osserviamo subito che entrambi i radicali sono positivi e quindi anche il loro prodotto sarà positivo. Infatti, entrambi i radicali hanno indice pari.
Determiniamo le condizioni di esistenza. Per ciascun radicale dovremo avere il radicando maggiore o al più uguale a zero. Si ha:
3+x \geq 0 \iff x \geq -3; \qquad 4-x \geq 0 \iff x \leq 4
Imponendo entrambe le condizioni contemporaneamente otteniamo le condizioni di esistenza del prodotto:
\begin{cases} x \geq -3 \\ \\ x \leq 4 \end{cases} \quad \Rightarrow \quad -3 \leq x \leq 4 Così per le condizione date possiamo scrivere:
\begin{align*} & \sqrt{3+x} \cdot \sqrt[4]{4-x}=\sqrt[4]{(3+x)^2} \cdot \sqrt[4]{4-x}= \\ \\ & =\sqrt[4]{(3+x)^2(4-x)}, \qquad -3 \leq x \leq 4 \end{align*}Esercizio 6
Veniamo all’ultimo di questi esercizi sul prodotto e quoziente di radicali con indici diversi. Calcolare:
\sqrt[3]{\dfrac{a+3}{a-3}} \cdot \sqrt{\dfrac{a-3}{a+1}} \cdot \sqrt[4]{\dfrac{a+1}{a+3}}Determiniamo anzitutto il campo di esistenza di ciascun radicale. Per il primo, che ha indice dispari, bisogna imporre la sola condizione relativa al denominatore diverso da zero:
a-3 \neq 0 \iff a \neq 3
Per gli altri radicali (di indice pari), dovremo imporre anzitutto i denominatori dei radicandi diversi da zero:
a+1 \neq 0 \iff a \neq -1; \quad a+3 \neq 0 \iff a \neq -3
e inoltre dovremo imporre i radicandi positivi o al più nulli:
\dfrac{a-3}{a+1} \geq 0 \quad \wedge \quad \dfrac{a+1}{a+3} \geq 0Studiamo il segno di ciascuna frazione, ad esempio per via grafica. Cominciamo dalla prima frazione:
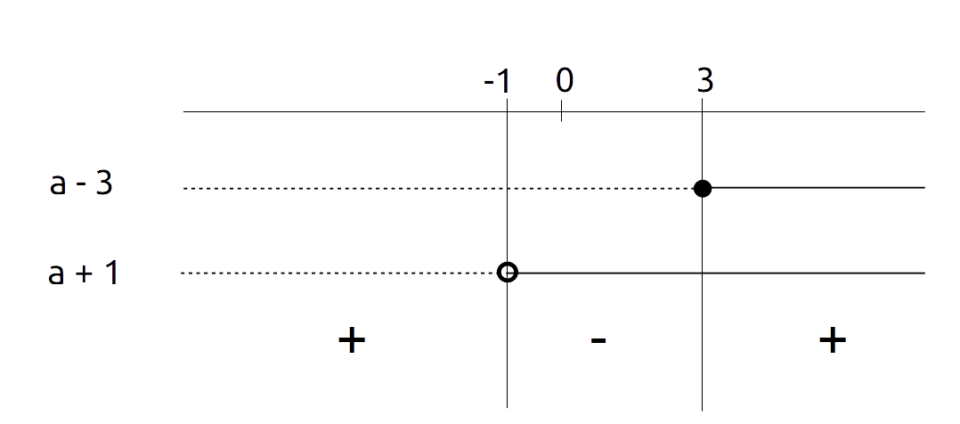
Per la seconda frazione:
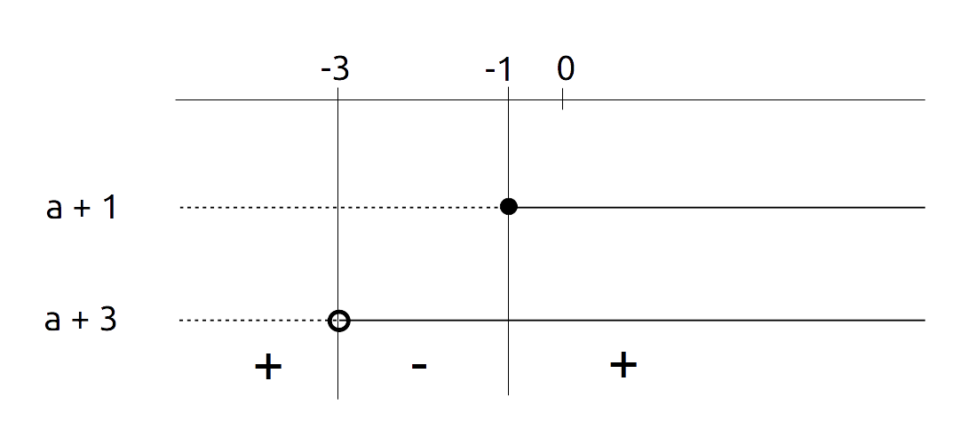
Prestiamo attenzione che dobbiamo escludere anche il valore {x=3} perché ciò è richiesto dalla condizione di esistenza del primo radicale. Inoltre dobbiamo anche escludere i valori che annullano i denominatori. Infine, per ciascuna frazione dobbiamo considerare i valori che le rendono positive o al più nulle.
Così, mettendo tutte le condizioni che devono valere contemporaneamente a sistema, abbiamo:
\scriptsize\begin{cases} a \neq 3 \\ \\ a \neq -1 \\ \\ a \neq -3 \\ \\ a < -1 \quad \vee \quad a \geq 3 \\ \\ a < -3 \quad \vee \quad a \geq -1\end{cases} \: \Rightarrow \quad \begin{cases}a < -1 \quad \vee \quad a > 3 \\ \\ a < -3 \quad \vee \quad a > -1 \end{cases} \: \Rightarrow \quad \boxed{ a <-3 \: \vee \: a > 3}e questa è la condizione di esistenza del prodotto.
Veniamo al segno del prodotto, riprendendo il prodotto di partenza. Osserviamo che il secondo e il terzo radicale sono positivi in quanto hanno indice pari. Il primo radicale potrà essere invece anche negativo, in quanto il suo indice è dispari e il radicando può assumere segno qualsiasi, in funzione della {a}.
Di conseguenza, il segno del prodotto dipenderà dal segno del radicando nel primo radicale. Effettuiamo allora lo studio del segno della frazione {\dfrac{a+3}{a-3}}:
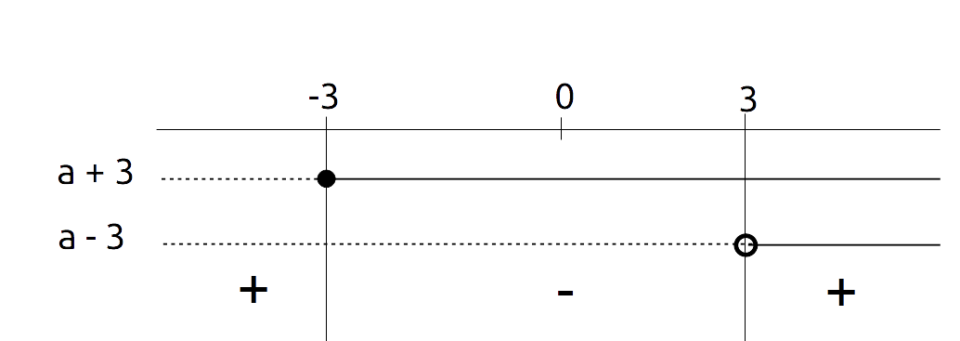
Osserviamo che la frazione e quindi il corrispondente radicale sono positivi in tutto il campo di esistenza del prodotto. Quindi, visto che gli altri due radicali sono sempre positivi, concludiamo che il prodotto è positivo in tutto il suo campo di esistenza.
In conclusione, imponendo la condizione di esistenza {a <-3 \: \vee \: a > 3} possiamo calcolare il prodotto come:
\begin{align*} &\sqrt[3]{\dfrac{a+3}{a-3}} \cdot \sqrt{\dfrac{a-3}{a+1}} \cdot \sqrt[4]{\dfrac{a+1}{a+3}}= \\ \\ & = \sqrt[12]{\dfrac{(a+3)^4}{(a-3)^4}} \cdot \sqrt[12]{\dfrac{(a-3)^6}{(a+1)^6}} \cdot \sqrt[12]{\dfrac{(a+1)^3}{(a+3)^3}}= \\ \\ & =\sqrt[12]{\dfrac{(a+3)^{\cancel{4}}}{\cancel{(a-3)^4}} \cdot\dfrac{(a-3)^{\cancel{6}^{\scriptsize \displaystyle2}}}{(a+1)^{\cancel{6}^{\scriptsize \displaystyle3}}}\cdot \dfrac{\cancel{(a+1)^3}}{\cancel{(a+3)^3}}} =\\ \\ & = \sqrt[12]{\dfrac{(a+3)(a-3)^2}{(a+1)^3}}, \qquad a<-3 \: \vee \: a > 3\end{align*}Per quanto riguarda gli esercizi sul prodotto e quoziente di radicali con indici diversi è tutto. Buon proseguimento con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
