Esercizi sulle equazioni irrazionali

 - 

Equazioni (superiori)

Proponiamo ora una scheda di esercizi sulle equazioni irrazionali, svolti e commentati. In questo modo potremo mettere ulteriormente in pratica quanto visto nella lezione teorica sulle equazioni irrazionali. Vedremo in particolare come risolvere le equazioni irrazionali nei vari casi possibili.

Ricordiamo brevemente che le equazioni irrazionali sono particolari equazioni algebriche nelle quali l’incognita compare almeno una volta sotto radice. L’idea per risolvere tali equazioni consiste nel liberare l’incognita dal simbolo di radice. In particolare, se nell’equazione compare la radice n-esima dell’incognita, è intuitivo elevare la quantità che contiene l’incognita all’esponente n. In tal modo sarà possibile isolare l’incognita come in una qualunque equazione algebrica. Tuttavia, occorre procedere in modo da rispettare i principi di equivalenza ed inoltre è fondamentale distinguere i casi di indice n pari oppure dispari.

Uno fra i casi più semplici è quello di equazioni irrazionali della forma:

\sqrt[n]{f(x)}=g(x), \qquad n \: \text{dispari}

In tal caso possiamo facilmente liberarci del simbolo di radice elevando entrambi i membri dell’equazione all’esponente n:

\left( \sqrt[n]{f(x)}\right)^n=\left( g(x)\right)^n

ottenendo:

f(x)=\left( g(x)\right)^n

A questo punto sarà possibile risolvere l’equazione nell’incognita {x}. E le sue eventuali soluzioni saranno anche soluzioni dell’equazione irrazionale di partenza.

Più complicato è il caso di equazioni irrazionali di questa stessa forma ma con indice n pari:

\sqrt[n]{f(x)}=g(x), \qquad n \: \text{pari}

Poiché le potenze con esponente pari non conservano necessariamente il segno della base, per essere sicuri di non incorrere in soluzioni estranee è necessario imporre la condizione di concordanza dei segni tra il primo e il secondo membro dell’equazione. Dato che il primo membro essendo una radice con indice pari è necessariamente positivo, tale condizione si esprime con:

g(x) \geq 0 

Di conseguenza, per risolvere l’equazione potremo anche in questo caso elevare entrambi i membri all’esponente n, tuttavia a patto di imporre contemporaneamente la condizione di concordanza dei segni:

\begin{cases}\left( \sqrt[n]{f(x)}\right)^n=\left( g(x)\right)^n \\ \\ g(x) \geq 0  \end{cases}

In altre parole si tratterà di risolvere l’equazione a sistema accettando le sole soluzioni che rispettano la condizione {g(x) \geq 0}. E tali soluzioni saranno anche soluzioni per l’equazione irrazionale di partenza.

Sempre nel caso di esponente n pari, in presenza di equazioni ad esempio della forma:

\sqrt[n]{f_1(x)} =\sqrt[n]{f_2(x)}, \qquad n \: \text{pari}

non è più necessario imporre la condizione di concordanza dei segni. Infatti, dato che n è pari è ovvio che entrambi i membri sono positivi. Tuttavia, in questo caso occorre imporre le condizioni di realtà dei radicali:

\begin{cases} f_1(x) \geq 0 \\ \\ f_2(x) \geq 0 \end{cases}

Così potremo ancora una volta risolvere l’equazione elevando all’esponente {n} entrambi i suoi membri, ma a patto di imporre contemporaneamente le condizioni di realtà dei radicali:

\begin{cases}\left(\sqrt[n]{f_1(x)}\right)^n  =\left(\sqrt[n]{f_2(x)} \right)^n \\ \\ f_1(x) \geq 0 \\ \\ f_2(x) \geq 0  \end{cases}

ovvero:

\begin{cases} f_1(x)=f_2(x) \\ \\ f_1(x) \geq 0 \\ \\ f_2(x) \geq 0  \end{cases}

Così si tratterà di risolvere l’equazione presente a sistema accettando soltanto le soluzioni tali da rispettare entrambe le condizioni di realtà poste.

Infine, precisiamo ancora una volta che in equazioni del tipo {\sqrt[n]{f(x)}=g(x)} la condizione di realtà del radicale non serve. Questa è infatti già inclusa nell’equazione che si ottiene elevando al quadrato entrambi i membri dell’equazione di partenza.

Fatte le dovute premesse, vediamo allora subito questi esercizi sulle equazioni irrazionali.

Esercizi svolti sulle equazioni irrazionali

Prima parte: equazioni irrazionali con un radicale e una quantità funzione dell’incognita

In questa prima parte ci proponiamo di risolvere equazioni irrazionali della forma:

\sqrt[n]{f(x)}=g(x)

Esercizio 1

Risolvere la seguente equazione irrazionale:

\sqrt[3]{1+8x^3}=3+2x

Eleviamo entrambi i membri all’indice del radicale al primo membro. Eleviamo quindi al cubo ciascun membro dell’equazione:

\left( \sqrt[3]{1+8x^3}\right)^3=\left( 3+2x\right)^3

Dato che l’indice del radicale è dispari, non dobbiamo imporre alcuna condizione. Sviluppando allora i calcoli in ciascun membro abbiamo:

1+8x^3=27+8x^3+36x+24x^2

Osserviamo che al secondo membro abbiamo calcolato il cubo di un binomio.

Procediamo riducendo l’equazione appena scritta alla forma normale:

24x^2+36x+26=0

ovvero:

12x^2+18x+13=0

Determiniamo le eventuali soluzioni:

x_{1,2}=\dfrac{-18\pm \sqrt{18^2-4 \cdot 12 \cdot 13}}{2 \cdot 12}=\text{impossibile}

L’equazione non ammette soluzioni poiché la quantità sotto radice (il determinante) è minore di zero. Quindi l’equazione di secondo grado è impossibile ed in conclusione è impossibile anche l’equazione irrazionale di partenza.

Esercizio 2

Risolvere:

\sqrt[3]{-1-3x^2}=x-1

Possiamo elevare al cubo entrambi i membri dell’equazione senza imporre alcuna condizione. Infatti, come nel caso precedente l’esponente del radicando al primo membro è dispari:

\left(\sqrt[3]{-1-3x^2}\right)^3=(x-1)^3

Abbiamo:

-1-3x^2=x^3+2x-2x^2-1

ovvero semplificando:

x^3+x^2+2x=0

Eseguiamo un raccoglimento al primo membro per poi applicare la legge di annullamento del prodotto:

x(x^2+x+2)=0 \quad \Rightarrow \quad x=0 \quad \vee \quad x^2+x+2=0

Abbiamo così intanto ottenuto la soluzione {x=0}. Risolviamo ora l’equazione:

x^2+x+2=0

Abbiamo:

x_{1,2}=\dfrac{-1 \pm \sqrt{1^2-4 \cdot 1 \cdot 2}}{2 \cdot 1}= \text{impossibile} 

Di conseguenza per l’equazione irrazionale di partenza abbiamo l’unica soluzione:

x=0

Esercizio 3

Vediamo ora come risolvere la seguente equazione irrazionale:

\sqrt{x+1}=x-1

Stavolta ci ritroviamo nel caso di indice del radicando pari. Infatti, al primo membro abbiamo una radice quadrata (indice {n=2}).

In questo caso non possiamo precipitarci ad elevare direttamente entrambi i membri al quadrato. Dobbiamo infatti imporre anche la condizione di concordanza dei segni tra il primo e il secondo membro. Infatti la quantità al secondo membro può avere in generale segno qualunque al variare della {x}.

Poiché il primo membro è positivo la condizione di concordanza dei segni consiste nell’imporre positivo o al più nullo il secondo membro:

x-1 \geq 0 

Di conseguenza l’equazione irrazionale di partenza è riconducibile al sistema:

\begin{cases}\left(\sqrt{x+1} \right)^2=(x-1)^2 \\ \\ x-1 \geq 0  \end{cases}

ovvero:

\begin{cases} x+1=x^2-2x+1 \\ \\ x \geq 1\end{cases}

Risolviamo a questo punto l’equazione a sistema accettando soltanto le soluzioni che soddisfano la condizione {x \geq 1}. Abbiamo:

 \small x+1=x^2-2x+1 \quad \Rightarrow \quad x^2-3x=0 \quad \Rightarrow \quad x(x-3)=0

Applicando la legge di annullamento del prodotto otteniamo per l’equazione di secondo grado le soluzioni:

x= 0 \quad \vee \quad x=3

Ora, attenzione. Non dimentichiamo la condizione {x \geq 1}, che è soddisfatta soltanto dalla soluzione {x=3}. Quindi, possiamo accettare per l’equazione irrazionale di partenza la sola soluzione {x=3}.

Esercizio 4

Veniamo ora alla seguente equazione irrazionale, sempre simile alle precedenti:

6-2x=x-\sqrt{4+x^2}-1

Per cominciare trasportiamo i termini in modo da ricondurci alla forma {\sqrt{f(x)}=g(x)}:

\sqrt{4+x^2}=6-2x-x+1

ovvero:

\sqrt{4+x^2}=-3x+7

In pratica abbiamo fatto in modo da avere tutte le quantità fuori radice al secondo membro.

Ora eleviamo entrambi i membri al quadrato, imponendo allo stesso tempo la condizione di concordanza dei segni (infatti l’indice del radicale è pari):

\begin{cases}4+x^2=9x^2+49-42x \\ \\ -3x + 7 \geq 0  \end{cases}

e quindi:

\begin{cases} 8x^2-42x+45=0 \\ \\ x \leq \dfrac{7}{3}\end{cases}

Risolviamo l’equazione a sistema accettando le sole soluzioni che rispettano la condizione {x \leq \dfrac{7}{3}}:

x_{1,2}=\dfrac{42 \pm \sqrt{42^2-4 \cdot 8 \cdot 45}}{2 \cdot 8}=\dfrac{42 \pm 18}{16}=\begin{cases}\dfrac{15}{4} \\ \\ \dfrac{3}{2} \end{cases}

Ora rimane da vedere quale delle due soluzioni rispetta la condizione {x \leq \dfrac{7}{3}}. Per fare questo dobbiamo confrontare tra loro tutte e tre le frazioni. Per fare ciò non è necessaria la calcolatrice: basta ridurre le frazioni a denominatore comune. Il primo passo consiste nel determinare il minimo comune multiplo fra tutti i denominatori. Poi, basterà riscrivere ciascuna frazione come la corrispondente frazione equivalente avente per denominatore proprio il denominatore comune trovato.

\text{mcm}(3,4,2)=12, \qquad \dfrac{7}{3}=\dfrac{28}{12}; \qquad \dfrac{15}{4}=\dfrac{45}{12}; \qquad \dfrac{3}{2}=\dfrac{18}{12}

Come è ora evidente, l’unica soluzione accettabile è {x=\dfrac{15}{4}}, che è così l’unica soluzione per l’equazione irrazionale di partenza.

Seconda parte: equazioni irrazionali con due radicali

Vediamo ora come risolvere le equazioni irrazionali della forma:

\sqrt[n]{f_1(x)}=\sqrt[n]{f_2(x)}

Esercizio 5

Risolvere la seguente equazione irrazionale con due radicali:

\sqrt[3]{4-x}=\sqrt[3]{2x+5}

Osserviamo che l’indice dei radicali è dispari. Di conseguenza non dobbiamo porre nessuna condizione, e possiamo direttamente elevare al cubo ciascun membro dell’equazione data:

4-x=2x+5

Riscriviamo l’equazione così ottenuta in forma normale:

3x+1=0

Otteniamo la soluzione:

x=-\dfrac{1}{3}

che è anche soluzione per l’equazione irrazionale di partenza.

Esercizio 6

Risolvere:

\sqrt{1+5x}=\sqrt{x-2}

Attenzione: stavolta gli indici dei radicali sono pari. Dobbiamo allora imporre le condizioni di realtà, una per ciascun radicale. In pratica dobbiamo imporre che tutte le quantità all’interno dei simboli di radice siano positive o al più nulle:

\begin{cases} 1+5x \geq 0 \\ \\ x-2 \geq 0\end{cases}

Sotto queste ipotesi è possibile elevare entrambi i membri al quadrato:

1+5x=x-2

Risolvendo l’equazione di primo grado otteniamo la soluzione:

x=-\dfrac{3}{4}

che è anche l’unica soluzione dell’equazione irrazionale di partenza.

Esercizio 7

Proseguiamo ancora con gli esercizi sulle equazioni irrazionali del tipo i precedenti. Vedremo tuttavia che in questo caso le condizioni di realtà richiederanno un po’ più lavoro. Risolviamo l’equazione:

\sqrt{-x^2-x+2}=\sqrt{x^2-x-6}

Come nell’esercizio precedente eleviamo entrambi i membri dell’equazione al quadrato imponendo allo stesso tempo le condizioni di realtà dei radicali (indici pari):

\begin{cases}-x^2-x+2=x^2-x-6 \\ \\ -x^2-x+2 \geq 0 \\ \\ x^2-x-6 \geq 0  \end{cases}

ovvero:

\begin{cases}2x^2=8  \quad \Rightarrow \quad x_{1,2}=\pm \sqrt{4}=\pm2 \\ \\  -x^2-x+2 \geq 0 \\ \\ x^2-x-6 \geq 0  \end{cases}

A questo punto dobbiamo lavorare sulle condizioni di realtà dei radicali, in modo da ricavare un’unica condizione da poter confrontare con le soluzioni appena ottenute per l’equazione di secondo grado.

Osserviamo che ciascuna condizione di realtà è del tipo:

P(x) \geq 0 

ove {P(x)} è un polinomio di secondo grado.

L’idea è quella di scomporre ciascun polinomio in fattori per poi studiare il segno di ciascun prodotto. In alternativa è anche possibile determinare gli zeri di ciascuna equazione {P(x)=0} e quindi utilizzare il metodo della parabola, risolvendo ciascuna disequazione {P(x) \geq 0}.

Vediamo il metodo basato sullo studio dei segni.

Cominciamo studiando il segno del polinomio {-x^2-x+2}. Per fare questo, scomponiamolo in fattori ad esempio utilizzando il metodo del trinomio caratteristico. Abbiamo:

\begin{align*} & -x^2-x+2=-(x^2+x-2)=-(x+2)(x-1)= \\ \\ & =(x+2)(1-x) \end{align*}

Studiamo il segno di ciascun fattore per poi determinare il segno del prodotto al variare di {x}:

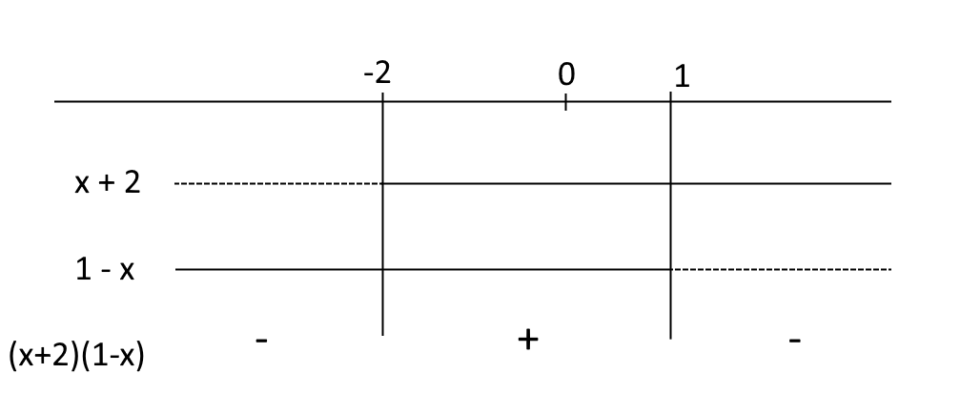
Così sappiamo che il polinomio {-x^2-x+2} è positivo per {-2 < x < 1} (ed è nullo in corrispondenza degli zeri).

Procediamo allo stesso modo con il polinomio {x^2-x-6}, che riguarda la rimanente condizione di realtà dei radicali. Abbiamo:

 x^2-x-6 =(x-3)(x+2)

Studiando i segni dei fattori:

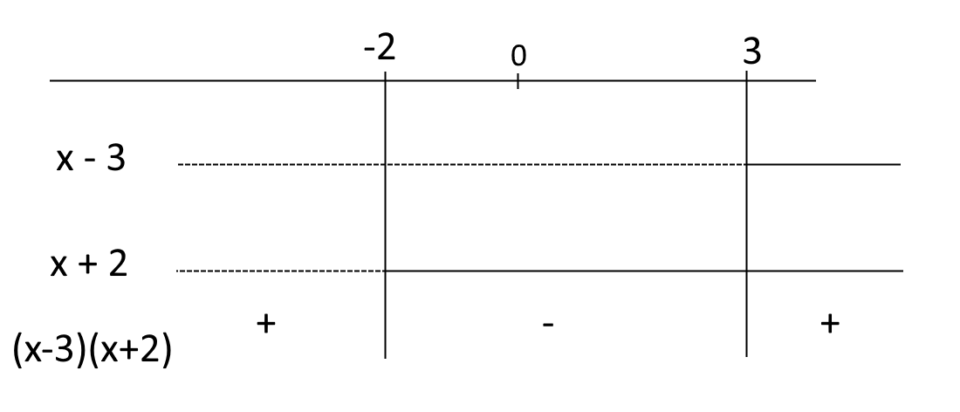
Il polinomio è positivo per {x < -2} oppure per {x > 3} (ed è nullo in corrispondenza degli zeri).

Ora non resta che intersecare tra di loro gli insiemi dei valori delle {x} che soddisfano le condizioni di realtà. Si tratta proprio dei due insiemi di valori che abbiamo appena determinato con gli studi dei segni.

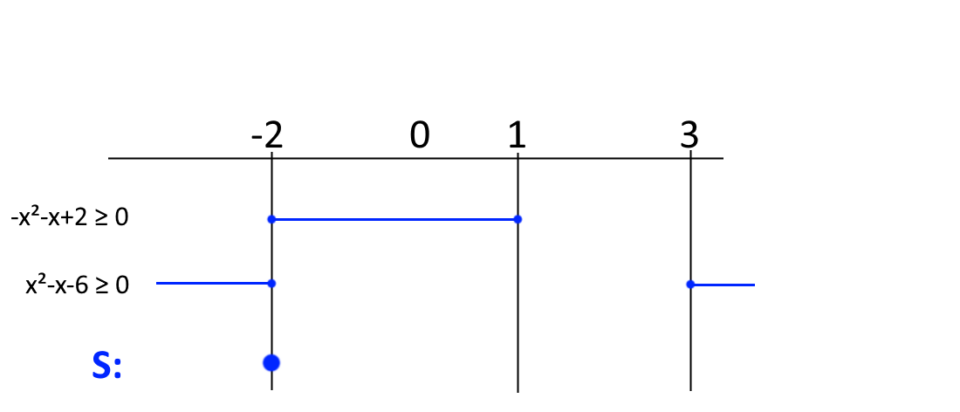
Come possiamo vedere, intersecando i due insiemi otteniamo l’insieme {S}, costituito da un unico elemento. Di conseguenza, entrambe le condizioni di realtà sono soddisfatte soltanto dal valore {x=2}.

In conclusione, poiché tra le soluzioni dell’equazione a sistema abbiamo il valore {x=2}, concludiamo che esso è la soluzione dell’equazione irrazionale di partenza.

Concludiamo questa scheda di esercizi sulle equazioni irrazionali con un paio di esercizi relativi ai casi di equazioni contenenti più di due radicali, oppure due radicali più un termine noto. Vedremo quindi come risolvere le equazioni irrazionali della forma:

\sqrt[n]{f_1(x)}+\sqrt[n]{f_2(x)}=k, \qquad k \in \mathbb{R}

e della forma:

\sqrt[n]{f_1(x)}+\sqrt[n]{f_2(x)} = \sqrt[n]{f_3(x)}

Osserviamo che se le equazioni non si presentano in forme esattamente di questo tipo, sarà in generale possibile ricondurle alle forme appena indicate utilizzando i principi di equivalenza. In altre parole, potrà accadere che dovremo trasportare dei termini da un membro all’altro dell’equazione in modo da ricondurci alle forme tipo appena presentate.

Precisiamo che le forme presentate sono quelle più convenienti per risolvere le equazioni con il minor numero di calcoli possibile.

Terza parte: equazioni irrazionali con più di due radicali o con due radicali più un termine noto

Esercizio 8

Veniamo al penultimo di questi esercizi sulle equazioni irrazionali:

\sqrt{1-x}+\sqrt{6-x}=5

Attenzione: sarebbe una cattiva idea trasportare uno dei due radicali al secondo membro:

\sqrt{1-x}=-\sqrt{6-x}+5

Infatti, così facendo la quantità a secondo membro potrà essere positiva, negativa o nulla a seconda del valore della {x}. Di conseguenza, dovremmo imporre la condizione di concordanza tra i segni dei membri dell’equazione.

Come visto in precedenti esercizi, osserviamo che il primo membro è positivo poiché si tratta di un radicale con indice pari. Dovremmo quindi imporre il secondo membro maggiore o uguale a zero, il che corrisponde alla condizione:

-\sqrt{6-x}+5 \geq 0 

ovvero:

\sqrt{6-x} \leq 5

Come evidente, la condizione corrisponde ad una disequazione irrazionale che ancora non sappiamo risolvere. In particolare, non è certamente desiderabile dover risolvere una disequazione irrazionale per risolvere un’equazione irrazionale. Comprendiamo quindi come è decisamente conveniente mantenere l’equazione data nella forma:

\sqrt{1-x}+\sqrt{6-x}=5

In questo modo infatti non è necessaria alcuna condizione di concordanza dei segni. Procediamo elevando entrambi i membri dell’equazione al quadrato, imponendo allo stesso tempo le condizioni di realtà dei radicali:

\begin{cases} \left( \sqrt{1-x}+\sqrt{6-x}\right)^2=5^2 \\ \\ 1- x \geq 0 \\ \\ 6 - x \geq 0 \end{cases}

ovvero:

\begin{cases} 1-x+6-x+2 \cdot \sqrt{1-x} \cdot \sqrt{6-x}=25 \\ \\ x \leq 1 \\ \\ x \leq 6\end{cases}

e quindi:

\begin{cases} 1-2x+6+2 \cdot \sqrt{(1-x)(6-x)}=25 \\ \\ x \leq 1\end{cases}

Si tratterà così di risolvere l’equazione irrazionale a sistema, accettando le sole soluzioni che soddisfano la condizione {x \leq 1 }. Abbiamo:

\begin{cases} -2x+2 \sqrt{6-x-6x+x^2}=18  \\ \\ x \leq 1 \end{cases}

ovvero, riconducendo l’equazione irrazionale ad una delle forme a noi note:

\begin{cases}\sqrt{x^2-7x+6}=9+x\\ \\ x \leq 1 \end{cases}

Ora, per l’equazione irrazionale a sistema dobbiamo scrivere un ulteriore sistema:

\begin{cases}x^2-7x+6=81+x^2+18x \\ \\ x \geq - 9 \end{cases}

Ciò corrisponde alle tecniche precedentemente viste per risolvere le equazioni irrazionali della forma {\sqrt[n]{f(x)} = g(x)}.

Sviluppando i calcoli abbiamo:

\begin{cases} 25x=-75 \\ \\ x \geq -9\end{cases} \quad \Rightarrow \quad \begin{cases}x = -3 \\ \\ x \geq - 9 \end{cases} \quad \Rightarrow \quad x = -3

Ora attenzione, non abbiamo ancora finito. Dobbiamo tornare indietro al primo sistema scritto. Quest’ultimo sistema infatti, non dimentichiamo, corrisponde soltanto all’equazione irrazionale presente nel primo sistema.

Dobbiamo quindi confrontare la soluzione {x=-3} appena ottenuta con la condizione {x \leq 1} presente nel primo sistema. Effettivamente la soluzione soddisfa tale condizione, quindi in conclusione l’equazione irrazionale di partenza è risolta per:

x = -3

Esercizio 9

Risolvere la seguente equazione irrazionale:

\sqrt{1+x}+\sqrt{4-x}=2

Siamo ancora in presenza di un’equazione irrazionale con indici dei radicali pari. Non abbiamo tuttavia bisogno di nessuna condizione di concordanza dei segni. Infatti entrambi i membri dell’equazione sono positivi per ogni valore della {x}. Procediamo quindi elevando al quadrato entrambi i membri dell’equazione, imponendo allo stesso tempo le condizioni di realtà dei radicali.

\begin{cases} 1+x + 2 \sqrt{(1+x)(4-x)} + 4-x = 4 \\ \\ 1+x \geq 0 \\ \\ 4-x \geq 0 \end{cases}

ovvero:

\begin{cases}  \sqrt{4+3x-x^2}=-\dfrac{1}{2}  \\ \\ 1 + x \geq 0 \\ \\ 4-x \geq 0 \end{cases}

Come possiamo notare immediatamente l’equazione a sistema è impossibile. Infatti, il primo membro (sempre positivo in quanto radicale con indice pari) non potrà mai essere uguale al secondo membro (una costante negativa).

Di conseguenza l’equazione irrazionale di partenza è in conclusione impossibile, ovvero non ammette alcuna soluzione.

Ultima parte: equazioni con più di due radicali

Esercizio 10

Concludiamo questi esercizi sulle equazioni irrazionali con il seguente:

\sqrt{x-5}-\sqrt{x-2}=\sqrt{x}

Trasportando un termine abbiamo:

\sqrt{x-5}=\sqrt{x}+\sqrt{x-2}

Eleviamo al quadrato entrambi i membri dell’equazione così riscritta, imponendo allo stesso tempo le condizioni di realtà dei radicali:

\begin{cases} x-5=x+2\sqrt{x(x-2)}+x-2 \\ \\ x-5 \geq 0 \\ \\ x \geq 0 \\ \\ x-2 \geq 0 \end{cases}

ovvero:

\begin{cases}2\sqrt{x(x-2)} = -3-x \\ \\ x \geq 5 \\ \\ x \geq 0 \\ \\ x \geq 2 \end{cases}

E’ immediato osservare che l’equazione a sistema è impossibile. Infatti, il primo membro è sempre positivo mentre il secondo membro è sempre negativo. Di conseguenza è anche impossibile l’equazione irrazionale di partenza.

Conclusioni

Per quanto riguarda gli esercizi sulle equazioni irrazionali per questa scheda è tutto. Riassumendo evidenziamo l’importanza di distinguere tra le equazioni irrazionali che contengono indici dei radicali dispari e quelle che contengono indici dei radicali pari.

Inoltre, nell’ambito delle equazioni irrazionali aventi radicali con indici pari, è importante capire in base alla forma dell’equazione quali condizioni porre. In particolare, se siamo sicuri che entrambi i membri dell’equazione hanno lo stesso segno bisogna imporre le sole condizioni di realtà dei radicali. Diversamente, occorre imporre l’opportuna condizione di concordanza dei segni fra i membri dell’equazione.

Buon proseguimento con SìMatematica!