Funzioni lineari di due variabili

 - 

Domini piani

Le funzioni lineari di due variabili sono funzioni a valori reali generalmente definite in tutto il piano ma il cui dominio può essere ristretto ad una regione del piano (dominio piano) e tali che il grado rispetto a ciascuna delle lettere presenti nell’espressione della funzione (variabili) è non superiore ad uno.

Le funzioni lineari di due variabili hanno la seguente espressione in forma generale:

f(x,y)=ax+by+c, \qquad a, \: b, \: c \in \R

Tali funzioni associano a ciascuna coppia {(x, y)} il corrispondente valore {f(x,y)}, calcolato secondo l’espressione {ax+by+c}.

Osserviamo che l’espressione {ax+by+c} ha senso per qualunque valore reale delle variabili {x} e {y}. Di conseguenza la funzione {f(x,y)} su indicata ha come dominio l’insieme dato da tutte le possibili coppie {(x,y)}, con {x, \: y \in \R}. In altre parole, il dominio di {f(x,y)} è dato da {\R \times \R}, ovvero {\R^2}. Infatti, ciascuna coppia {(x,y)} è un elemento dell’insieme che si ottiene dal prodotto cartesiano di {\R} con sé stesso:

\R \times \R = \R ^2

Così tenendo conto del suo dominio possiamo definire {f(x,y)} come segue:

f(x,y):\R^2 \rightarrow \R, \quad (x,y) \rightarrow ax+by+c

Ma se la funzione {f(x,y)} è definita in tutto {\R^2} allora sarà anche definita in un sottoinsieme di {\R^2}. Per cui, un qualsiasi dominio piano è un possibile dominio per {f(x,y)}.

Dal punto di vista grafico, le funzioni lineari di due variabili hanno come grafico un piano inclinato che vive nello spazio tridimensionale. Ad esempio, per la funzione lineare di due variabili:

f(x,y)=3x+6y-7

che è della forma {f(x,y)=ax+by+c} con {a=3, \: b = 6, \: c=-7} abbiamo il seguente grafico:

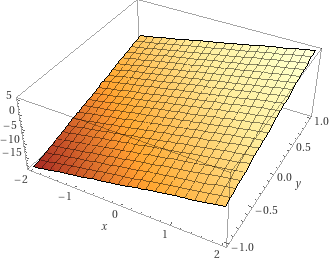
Osserviamo che il dominio della funzione è una regione del piano coordinato {x-y}, ovvero il piano in cui giacciono entrambi gli assi {x} e {y}. Ciascun punto del grafico della funzione si ottiene calcolando il valore assunto da {f(x,y)} in ciascuna coppia di punti {(x,y)} del piano coordinato {x-y}, riportando opportunamente il valore ottenuto nell’asse {z} (l’asse verticale).

Ora poniamo:

ax+by+c=k, \qquad k \in \R

Esplicitando ad esempio rispetto ad {y} otteniamo:

y=\dfrac{-ax-c+k}{b}

ovvero:

y=-\dfrac{a}{b}x+\dfrac{-c+k}{b}

A prima vista ci ritroviamo con l’equazione di una retta, della forma {y=mx+q}, con {m=-\dfrac{a}{b}} e {q=\dfrac{-c+k}{b}}. E’ però importante osservare che mentre i coefficienti {a, \: b, \:c } sono noti (dipendono infatti dall’espressione di {f(x,y)}), la lettera {k} può assumere qualsiasi valore reale ed è dunque un parametro.

Così, la precedente espressione non rappresenta soltanto una retta ma un fascio improprio di rette. In altre parole, abbiamo delle rette tutte parallele tra loro (infatti hanno tutte lo stesso coefficiente angolare {m=-\dfrac{a}{b}}) e con ordinata all’origine {q} dipendente dal parametro {k}.

Osservazione. Il fascio è detto “improprio” poiché le rette che lo compongono sono tutte parallele tra loro.

Tale fascio di rette è anche rappresentato dall’espressione data inizialmente, ovvero:

ax+by+c=k, \qquad k \in \R

E’ importante rilevare che, fissato un certo {k}, tutti i valori {x, \: y} tali da soddisfare la precedente uguaglianza rappresentano i punti del piano per i quali la funzione {f(x,y)} assume il valore reale {k}. Così, fissando un certo {k_0}, in tutti i punti della retta {ax+by+c=k_0} la funzione {f(x,y)} assume lo stesso valore.

Massimi e minimi delle funzioni lineari di due variabili in un dominio piano

Consideriamo una funzione lineare di due variabili definita in un dominio piano {D_f}:

f(x,y):D_f \subseteq \R^2 \rightarrow \R

Restringiamoci al solo caso di domini piani delimitati da rette.

Il nostro obiettivo è determinare i punti del dominio {D_f} in corrispondenza dei quali la funzione assume rispettivamente il valore massimo e il valore minimo.

Per valore massimo (minimo) di una funzione in un dominio intendiamo il più grande (piccolo) valore assunto dalla funzione tra tutte le sue valutazioni in ciascun punto del dominio.

Ora, supponiamo di avere una funzione lineare di due variabili definita in un dominio piano dato da un poligono. Si può dimostrare quanto segue.

Consideriamo una funzione {f(x,y):D_f \subseteq \R^2 \rightarrow \R}, lineare di due variabili reali e a valori reali. Sia {D_f} un dominio piano delimitato da rette, ovvero un poligono.
Sotto tali ipotesi, i valori di massimo e minimo assunti dalla funzione relativamente al dominio {D_f} sono da ricercare fra le valutazioni della funzione in corrispondenza dei vertici del poligono e/o in corrispondenza di tutti i punti di uno o più lati del poligono.
In particolare, se in due stessi vertici la funzione assume uno stesso valore di massimo (minimo), allora in tutti i punti del segmento che unisce i due vertici la funzione assume tale valore di massimo (minimo).

Tutti i punti del dominio piano {D_f} nei quali la funzione {f(x,y)} assume valori di massimo o minimo relativamente a quel dominio si dicono punti di massimo o minimo della funzione, relativi al dominio {D_f}.

Ora, potremmo chiederci come mai può accadere che tutti i punti di un dato segmento che congiunge due vertici del dominio piano siano punti di massimo o minimo per la funzione.

Per comprendere questo basta riflettere su quanto affermato in precedenza, ovvero che ogni retta del tipo {ax+by+c=k_0} è data da punti del dominio {D_f} in corrispondenza dei quali {f(x,y)} assume lo stesso valore {k_0}. Di conseguenza, se il dominio {D_f} della funzione è tale che la retta passante per due suoi vertici ha lo stesso coefficiente angolare della retta {ax+by+c=k_0} per un opportuno {k_0}, ed inoltre se in corrispondenza di tali vertici la funzione assume uno stesso valore di massimo o di minimo, allora tutti i punti del segmento che congiunge tali vertici saranno necessariamente punti di massimo o di minimo.

Così in breve, per ricercare i punti di massimo e minimo di una funzione lineare di due variabili definita in un poligono, dobbiamo prima di tutto determinare le coordinate dei vertici del poligono. E le coordinate di ciascun vertice si ottengono intersecando tra loro due opportune rette del poligono.

Fatto ciò, dovremo procedere con il calcolare le valutazioni della funzione in ciascun vertice. Se in ciascun vertice otteniamo un valore differente, allora il punto di minimo sarà il vertice ove la funzione assume il valore più piccolo, mentre il punto di massimo sarà il punto ove la funzione assume il valore più grande.

Nel caso in cui invece la funzione assume un valore massimo (minimo) in corrispondenza di due vertici, tutti i punti del segmento che unisce i due vertici saranno punti di massimo (minimo).

Esempio 1 (massimi e minimi relativi di funzioni lineari di due variabili)

Determinare i massimi e minimi della funzione {f(x, y)=3x+9y-5} relativamente al dominio {D_f} delimitato dalle rette {\begin{align*} & r_1 : 2x+3y-5=0, \: r_2 : 2x+4y+2=0, \\ \\ & \: r_3 : -3x+6y-4=0, r_4: -3x+6y+5=0 \end{align*}} e comprendente anche i punti delle rette stesse.

Cominciamo tracciando nel piano cartesiano le rette {r_1, \: r_2, \: r_3, \: r_4}. Per fare questo, è utile riscrivere ciascuna equazione delle rette in forma esplicita:

\begin{align*} &r_1 : y=-\dfrac{2}{3}x+\dfrac{5}{3}; \\ \\&  r_2 :y =-\dfrac{1}{2}x-\dfrac{1}{2}; \\ \\ & r_3 : y = \dfrac{1}{2}x+\dfrac{2}{3} \\ \\ & r_4 :  y=\dfrac{1}{2}x-\dfrac{5}{6}\end{align*}

Per rappresentare ciascuna retta, come visto nelle precedenti lezioni basta considerare due punti appartenenti ad ogni retta. In particolare, basterà sostituire per ciascun punto un fissato valore della {x} in modo da ottenere il corrispondente valore {y}. Ciascuna coppia {(x,y)} così ottenuta rappresenta le coordinate di un punto della retta considerata.

Disegnando ciascuna retta nel piano cartesiano otteniamo la seguente rappresentazione grafica:

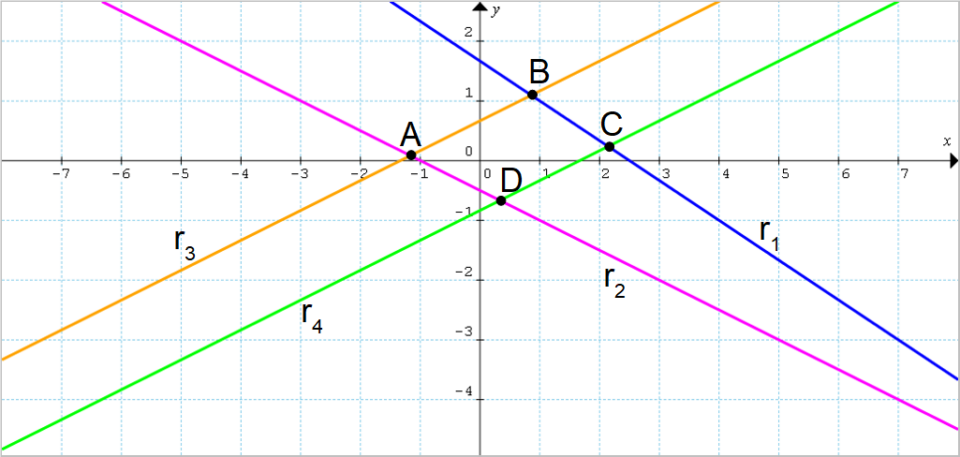
Le rette determinano il poligono {\overline{ABCD}}, che è il dominio piano {D_f} della funzione {f(x,y)}. Tale dominio ha la seguente rappresentazione analitica:

\begin{cases}2x+3y-5 \leq 0  \\ \\ 2x+4y+2 \geq 0 \\ \\ -3x+6y-4 \leq 0  \\ \\ -3x+6y+5 \geq 0 \ \end{cases}

I punti {A, \: B, \: C, \: D} sono i vertici del poligono e risultano dall’intersezione di due opportune rette. Ad esempio, il vertice {A} si ottiene dall’intersezione delle rette {r_2} ed {r_3}, il vertice {B} si ottiene dall’intersezione della retta {r_1} con la retta {r_3} e così via.

Per determinare le coordinate cartesiane di ciascun vertice basta mettere a sistema le equazioni delle rette la cui intersezione restituisce proprio quel vertice. Così abbiamo intanto, per il vertice {A}:

A:r_2 \cap r_3 : \begin{cases}r_2 : y =-\dfrac{1}{2}x-\dfrac{1}{2} \\ \\  r_3 : y = \dfrac{1}{2}x+\dfrac{2}{3}  \end{cases}

Possiamo risolvere il sistema utilizzando il metodo del confronto:

\begin{align*} &\begin{cases}-\dfrac{1}{2}x-\dfrac{1}{2} = \dfrac{1}{2}x + \dfrac{2}{3} \quad \rightarrow \quad x =  -\dfrac{7}{6} \\ \\ y=\dfrac{1}{2}x+\dfrac{2}{3} \quad \rightarrow \quad y=\dfrac{1}{12}\end{cases}\end{align*}

Così un primo vertice del poligono è dato da {A=\left( -\dfrac{7}{6}, \dfrac{1}{12}\right)}.

Procedendo in modo del tutto simile otteniamo per i rimanenti vertici le seguenti coordinate:

B=\left( \dfrac{6}{7}, \dfrac{23}{21}\right), \quad C=\left(\dfrac{15}{7}, \dfrac{5}{21}\right), \quad D=\left( \dfrac{1}{3}, -\dfrac{2}{3}\right)

Ora dobbiamo valutare la funzione {f(x, y)=3x+9y-5} in corrispondenza di ciascun vertice del dominio {D_f}. Tali valutazioni sono infatti tutte possibili massimi o minimi per la funzione relativi al dominio {D_f}. Abbiamo:

\small \begin{align*} &A: \quad f\left( x_A, y_A\right)=f\left( -\dfrac{7}{6}, \dfrac{1}{12}\right)=3 \cdot \left( -\dfrac{7}{6}\right)+9 \cdot \dfrac{1}{12}-5=-\dfrac{31}{4} \\ \\ &B: \quad f(x_B, y_B)=f\left( \dfrac{6}{7}, \dfrac{23}{21}\right)=3 \cdot \dfrac{6}{7}+9\cdot\dfrac{23}{21}-5=\dfrac{52}{7} \\ \\ &C: \quad f(x_C, y_C) = f\left(\dfrac{15}{7}, \dfrac{5}{21}\right)=3 \cdot \dfrac{15}{7}+9\cdot \dfrac{5}{21}-5=\dfrac{25}{7} \\ \\ & D: \quad f(x_D, y_D)=f\left(\dfrac{1}{3}, -\dfrac{2}{3} \right)=3 \cdot \dfrac{1}{3}+9\cdot \left( -\dfrac{2}{3}\right)-5=-10 \end{align*}

Tutti i valori appena calcolati sono diversi tra loro e di conseguenza non avremo punti di massimo o minimo in corrispondenza di nessun lato del poligono {D_f}.

Ricercando il valore più piccolo e il valore più grande tra le valutazioni della funzione appena calcolate, concludiamo che {D} è un punto di minimo della funzione relativo al dominio {D_f} mentre {B} è un punto di massimo della funzione sempre relativo al dominio {D_f}.

Esempio 2

Calcolare i massimi e minimi della funzione {f(x,y)=x-y+2} relativi al dominio {D_f} seguente.

D_f : \begin{cases}y \geq -3x-4  \\ \\ y \geq -1 \\ \\  y \leq  x+4 \\ \\  y \leq -3x+8\end{cases}

Le rette origine di ciascun semipiano a sistema sono:

\begin{align*} &r_1 : y=-3x-4,  && \quad r_2 : y=-1 \\ \\ & r_3:y=x+4, && \quad r_4:y=-3x+8\end{align*}

Rappresentiamo nel piano cartesiano il dominio piano come segue:

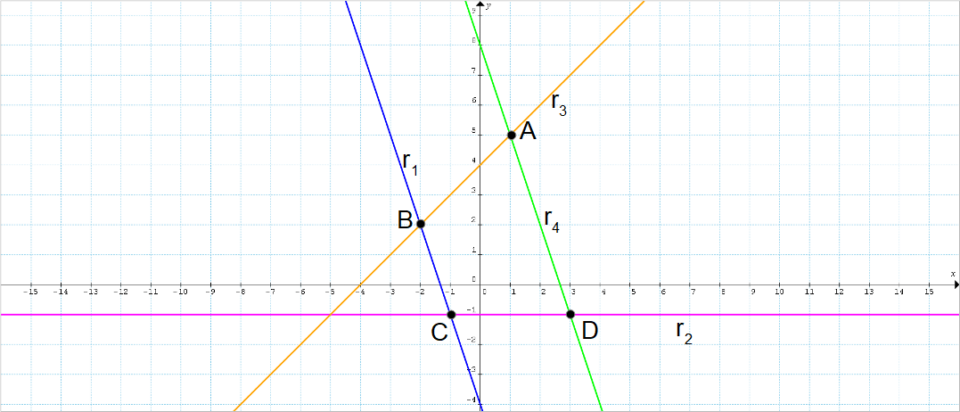
Il dominio piano è dato dal poligono {\overline{ABCD}}.

Determiniamo le coordinate dei vertici mettendo a sistema due a due le equazioni corrispondenti a ciascuna retta rappresentata in figura (omettiamo per brevità i passaggi relativi alla risoluzione dei sistemi):

\begin{align*} &A: r_3 \cap r_4 : \begin{cases} y=x+4 \quad \rightarrow \quad x=1 \\ \\ y=-3x+8 \quad \rightarrow  \quad y=5\quad \end{cases} \\ \\ & B: r_1 \cap r_3 : \begin{cases} y=-3x-4 \quad \rightarrow \quad x =-2  \\ \\ y=x+4 \quad \rightarrow \quad y=2\end{cases} \\ \\ &C: r_2 \cap r_1 : \begin{cases} y=-1 \\ \\ y=-3x-4 \quad \rightarrow \quad x=-1\end{cases}  \\ \\ &D: r_2 \cap r_4 : \begin{cases} y=-1 \\ \\ y=-3x+8 \quad \rightarrow \quad x=3\end{cases}\end{align*}

Così abbiamo i vertici:

\small A=(1,5), \quad B=(-2,2), \quad C=(-1, -1), \quad D=(3, -1)

Procediamo ora valutando la funzione in ciascun vertice, in modo da ricercare i punti di massimo e minimo relativi al dominio {D_f}:

\begin{align*} & f(x_A, y_A)= f(1,5)=1-5+2=-2 \\ \\& f(x_B, y_B) = f(-2, 2)=-2-2+2=-2 \\ \\ &f(x_C, y_C)=f(-1,-1)=-1+1+2=2 \\ \\ &f(x_D, y_D)=f(3,-1)=3+1+2=6\end{align*}

Il valore di massimo della funzione relativo al dominio {D_f} è {6} ed il corrispondente punto di massimo (sempre relativo al dominio {D_f}) è il vertice {D=(3,-1)}.

Osserviamo che per il minimo della funzione relativo al dominio {D_f} abbiamo il valore {-2} comune ai vertici {A} e {B}. Così tutti i punti del segmento {\overline{AB}} sono punti di minimo della funzione relativamente al dominio {D_f}.

Per fornire informazioni più precise sui punti di minimo relativo della funzione, scriviamo l’equazione della retta passante per i vertici {A} e {B}. Cominciamo calcolandone il coefficiente angolare:

m=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{2-5}{-2-1}=\dfrac{-3}{-3}=1

Di conseguenza, l’equazione di tale retta è:

\small y-y_A=m \cdot (x-x_A) \quad \rightarrow \quad y-5=x-1 \quad \rightarrow \quad y=x+4

Così, i punti di minimo relativi al dominio {D_f} della funzione data sono:

(x, x+4) \quad \text{con} \quad  -2 \leq x \leq 1 

ove la {x} è ristretta ai valori compresi tra le ascisse dei punti {A} e {B}. Ciò effettivamente corrisponde a tutti i punti appartenenti al segmento {\overline{AB}}.

Conclusioni

Qui termina la lezione sulle funzioni lineari di due variabili e sulla ricerca dei loro punti di massimo e minimo relativi ad un certo dominio piano {D_f} delimitato da rette.

Abbiamo così fornito un’introduzione alle funzioni di due variabili reali a valori reali, limitatamente al secondo anno delle scuole superiori. L’argomento verrà ripreso nelle lezioni di Analisi 2 dedicate agli studenti universitari. Buono studio a tutti voi!