Insieme complementare

 - 

Insiemi

L’insieme complementare di un insieme A rispetto ad un fissato universo E è l’insieme dato dagli elementi dell’insieme E che non appartengono all’insieme A. Effettivamente un tale insieme è il “complementare” dell’insieme A rispetto ad E, poiché l’unione tra detto insieme e l’insieme A restituisce proprio l’insieme universo E.

In questa lezione vediamo il concetto di insieme complementare di un dato insieme rispetto ad un fissato insieme universo {E}. E’ fondamentale ricordare che la nozione di insieme complementare deve sempre andare a braccetto con l’insieme universo scelto. In altre parole, ha senso parlare di insieme complementare di un dato insieme soltanto se si precisa l’insieme universo {E} che abbiamo scelto. Come vedremo infatti, nella simbologia utilizzata per gli insiemi complementari è sempre precisato l’insieme universo scelto.

Ricordiamo che l’insieme universo per uno o più insiemi {A_i} (con {i} numero naturale) è un insieme tale da essere un sovrainsieme per tutti gli insiemi {A_i}. In parole povere, perché l’insieme {E} sia un insieme universo ad esempio per gli insiemi {A, \: B, \: C}, tali insiemi dovranno essere tutti dei sottoinsiemi dell’insieme universo {E}:

\small E \: \text{insieme universo per} \: A, \: B, \: C \iff A \subseteq E \: \wedge B \subseteq E \: \wedge \: C \subseteq E

ove il simbolo “{\iff}” significa “se e solo se” e il simbolo “{\wedge}” significa “e contemporaneamente”. Ricordiamo inoltre che il simbolo “{\subseteq}” indica la relazione di inclusione tra insiemi (vedi sottoinsiemi).

Dopo questa breve introduzione, diamo inizio alla lezione vera e propria introducendo gradualmente la definizione di insieme complementare e i principali concetti ad essa correlati, fornendo regole ed esempi.

Definizione di insieme complementare

Supponiamo di dover lavorare unicamente con degli insiemi {A_i} (ovvero con gli insiemi {A_1, \: A_2, \: \dots \: A_n, \: n \in \N}), tali da essere tutti sottoinsiemi di un dato insieme {E}, che definiamo insieme universo o spazio ambiente.

Preso allora uno qualunque di tali insiemi {A_i}, che indicheremo semplicemente con {A}, vale la seguente definizione.

L’insieme complementare di un insieme {A} rispetto all’universo {E} è l’insieme che contiene tutti gli elementi dell’insieme {E} che non appartengono all’insieme {A}. In simboli:{\mathcal{C}_E A=\left\{ x \in E | x \not \in A\right\}}E per la definizione di insieme differenza:{\mathcal{C}_E A=E \setminus A}

Il simbolo {\mathcal{C}_E A} significa “insieme complementare di {A} rispetto all’universo scelto {\textbf{E}}“.

Osserviamo che un insieme complementare di {A} è univocamente determinato soltanto una volta precisato l’insieme universo {E}. E dato che in generale è possibile scegliere infiniti insiemi universo per l’insieme {A}, abbiamo per {A} infiniti insiemi complementari al variare del particolare insieme universo scelto. Ma una volta scelto ed espressamente indicato l’insieme universo {E}, l’insieme complementare di un insieme {A} rispetto all’insieme universo {E} è unico.

Infine, per la definizione di insieme complementare abbiamo evidentemente:

\mathcal{C}_EA \cup A = E

ovvero l’unione del complementare di un insieme {A} rispetto all’universo {E} e dello stesso insieme {A} restituisce l’insieme universo {E}. Infatti, abbiamo l’unione degli elementi di {E} che non appartengono ad {A} e degli elementi di {A}.

Insieme complementare e diagrammi di Venn

Fissato un insieme universo {E} per l’insieme {A} (avendo quindi {A \subseteq E}), possiamo rappresentare l’insieme complementare di {A} rispetto all’insieme universo {E} come segue (diagrammi di Venn:

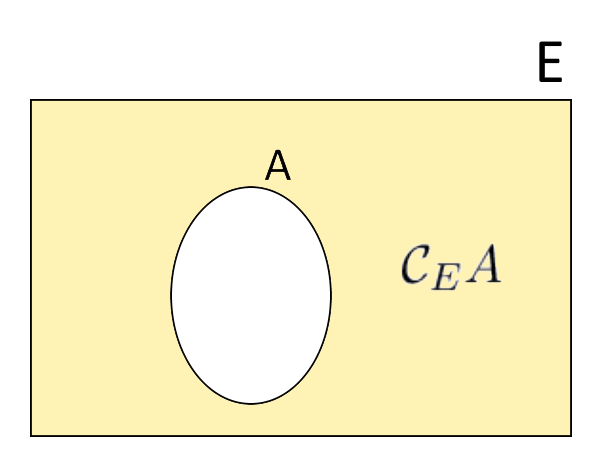
In pratica abbiamo rappresentato l’insieme universo {E} con un rettangolo. L’insieme {A} è rappresentato con il corrispondente ovale, mentre il complementare dell’insieme {A} rispetto all’universo {E} è dato dalla parte colorata.

Esempi sull’operazione di complementazione tra insiemi

Vediamo degli esempi su come determinare l’insieme complementare di un dato insieme A rispetto ad un fissato insieme universo E. L’operazione di determinare l’insieme complementare di un dato insieme (ovviamente rispetto ad un fissato insieme universo) si chiama complementazione.

Esempio 1

Dato l’insieme:

A=\left\{ 1,2,3\right\}

determinare il suo complementare rispetto all’universo {E=\left\{ 1,2,3,4,5\right\}}.

Per la definizione di insieme complementare, si tratta di determinare l’insieme differenza:

\mathcal{C}_E A = E \setminus A = \left\{ 1,2,3,4,5\right\}- \left\{ 1,2,3\right\}=\left\{ 4,5\right\}

Infatti {4, \: 5} sono gli elementi di {E} che non appartengono ad {A}. Così in conclusione:

\mathcal{C}_E A = \{4,5\}

Esempio 2

Determinare il complementare dell’insieme:

A=\left\{ x  < 10\right\}

prendendo come insieme universo l’insieme {\N} dei numeri naturali.

Cominciamo anzitutto rappresentando per comodità l’insieme {A} per elencazione (infatti in questo caso l’insieme {A} è finito):

A= \left\{ 0,1,2,3,4,5,6,7,8,9\right\}

Preso {E=\N}, abbiamo:

\mathcal{C}_E A = E - A = \N - \left\{ 0,1,2,3,4,5,6,7,8,9\right\}=\{x \in \N \: | \: x > 9\}

In altre parole, l’insieme cercato è l’insieme dei numeri naturali privato degli elementi da {0} a {9}. Ma un tale insieme è semplicemente l’insieme dei numeri naturali maggiori di {9}. Da cui la rappresentazione in forma implicita (o intensiva, o per proprietà caratteristica) utilizzata.

Così in conclusione abbiamo:

\mathcal{C}_E A = \left\{ x \in \N \: | \: x > 9\right\}

Esempio 3

Fissato come insieme universo l’insieme {\N} dei numeri naturali, determinare il complementare rispetto all’universo stesso dell’insieme dei numeri pari.

Indicato con {P} l’insieme dei numeri pari e con {D} l’insieme dei numeri dispari, per l’insieme complementare dell’insieme dei numeri pari rispetto all’universo dato dall’insieme dei numeri naturali, abbiamo:

\mathcal{C}_\N P=D

Osserviamo che vale sempre l’uguaglianza {\mathcal{C}_E A \cup A = E}. Ad esempio per quanto riguarda il terzo esempio abbiamo:

\mathcal{C}_{\N} P \cup P=D \cup P = \N

Così, lo ribadiamo ancora, l’unione di un insieme con il complementare dell’insieme rispetto ad un dato insieme universo restituisce lo stesso insieme universo.

Proprietà dell’insieme complementare

Vediamo ora le principali proprietà dell’insieme complementare (più precisamente, le principali proprietà dell’operazione di complementazione di un insieme).

1) Unione di un insieme e del suo complementare

Come già ormai evidenziato più volte, fissato un universo {E} e considerato un suo sottoinsieme {B} si ha:

B \cup \mathcal{C}_E B  = E

Effettivamente, possiamo riscrivere la precedente uguaglianza come segue:

\left\{ x \in E \: | \: x \in B\right\} \cup \left\{ x \in E \: | \: x \in E \: \wedge x \not \in B\right\}=E

uguaglianza che è evidentemente vera (basta applicare la definizione di insieme unione). Infatti abbiamo l’unione degli elementi dell’insieme {E} che appartengono all’insieme {B} e degli elementi dello stesso insieme {E} che non appartengono all’insieme {B}.

2) Intersezione tra un insieme e il suo complementare

Abbiamo:

B \cap \mathcal{C}_E B = \emptyset

Effettivamente per la definizione di insieme complementare i due insiemi {B} e {\mathcal{C}_E B} sono disgiunti, ovvero non hanno elementi in comune. Di conseguenza il risultato della loro intersezione è uguale all’insieme vuoto.

3) Leggi di de Morgan

Mettendo in relazione l’operazione di complementazione di un insieme rispetto ad un insieme universo e le operazioni di unione ed intersezione tra insiemi, otteniamo le leggi di De Morgan. Le uguaglianze a seguire sono valide nel caso in cui {E} sia il fissato insieme universo per due insiemi {A, \: B}.

3.1) Prima legge di De Morgan (legge dell’intersezione)

\mathcal{C}_E (A \cap B) = \mathcal{C}_E A \cup \mathcal{C}_E B

In altre parole, la prima legge di De Morgan afferma che l’insieme complementare dell’intersezione tra due insiemi è uguale all’unione del complementare del primo insieme e del complementare del secondo insieme.

3.2) Seconda legge di De Morgan (legge dell’unione)

\mathcal{C}_E (A \cup B)=\mathcal{C}_E A \cap \mathcal{C}_E B

La seconda legge di de Morgan afferma quindi che il complementare dell’unione tra insiemi è uguale all’intersezione dei rispettivi complementari di ciascuno dei due insiemi.

Per i più volenterosi, una dimostrazione delle leggi di De Morgan è disponibile qui (attenzione: nella risorsa nel link, l’insieme universo viene indicato con {U}, mentre {E} rappresenta un insieme generico). Osserviamo che dimostrare le leggi di De Morgan equivale a provare l’uguaglianza degli insiemi a primo e secondo membro dell’uguaglianza corrispondente a ciascuna legge. E ancora, l’uguaglianza tra due insiemi si dimostra provando che il primo insieme è un sottoinsieme del secondo e che contemporaneamente il secondo insieme è un sottoinsieme del primo. Ed è questo il succo dei ragionamenti utilizzati nel dimostrare le leggi di De Morgan.

Ma al di là delle dimostrazioni rigorose, è anche possibile dimostrare intuitivamente le leggi di De Morgan con una “dimostrazione grafica”, che però qui omettiamo.

Ricordiamo che le leggi di De Morgan date per gli insiemi sono perfettamente analoghe alle corrispondenti leggi di De Morgan date per le operazioni con le proposizioni logiche. In particolare, la complementazione tra insiemi corrisponde alla negazione logica di proposizioni.

4) Complementare dell’insieme vuoto e complementare dell’insieme universo

Il complementare dell’insieme vuoto rispetto ad un fissato universo {E} è uguale ad {E}:

\mathcal{C}_E \emptyset = E

Infatti, data la definizione di insieme complementare formulata con l’operazione di differenza tra insiemi, abbiamo:

\mathcal{C}_E \emptyset = E \setminus \emptyset = E 

Il complementare dell’insieme universo (rispetto allo stesso insieme universo) è uguale all’insieme vuoto:

\mathcal{C}_E E = \emptyset 

Infatti utilizzando ancora l’operazione di differenza tra insiemi:

\mathcal{C}_E E = E \setminus E = \emptyset

Di conseguenza, abbiamo tutti gli elementi di {E} che non appartengono all’insieme stesso {E}, e quindi l’insieme vuoto.

5) Complementare del complementare di un insieme

Il complementare del completare di un insieme A (rispetto ad un fissato universo E) restituisce lo stesso insieme A:

\mathcal{C}_E (\mathcal{C}_EA) = A

Infatti, l’operazione può essere ricondotta a:

\mathcal{C}_E (E \setminus A)

Ma il complementare degli elementi di {E} che non appartengono ad {A} non può essere dato che dagli elementi di {E} che appartengono ad {A}. E visto che {A \subseteq E} (per definizione di insieme universo), otteniamo l’insieme {A}.

In modo intuitivo, possiamo immaginare di prendere il negativo di un’immagine, e quindi di prenderne ancora il negativo. Il risultato che otteniamo non può essere che la stessa immagine di partenza. 😉

Conclusioni

A questo punto, conosciuta anche la complementazione abbiamo visto tutte le principali operazioni tra insiemi e le rispettive proprietà. Nella prossima lezione introdurremo la definizione di partizione di un insieme (che non è l’insieme delle parti di cui già ci siamo occupati). Nella lezione ancora successiva ci occuperemo infine del prodotto cartesiano, completando così la serie di lezioni sugli insiemi di SìMatematica! Buon proseguimento!