Intersezione tra insiemi

 - 

Insiemi

L’intersezione tra insiemi è un’operazione il cui risultato è un insieme costituito dai soli elementi in comune agli insiemi dati. Così l’insieme intersezione dei due insiemi A e B è uguale ad un insieme che contiene tutti e soli gli elementi che appartengono ad entrambi gli insiemi A e B.

Dopo aver visto l’operazione di unione tra insiemi, in questa lezione introduciamo quindi l’intersezione tra insiemi, fornendo la definizione, alcuni esempi ed infine riportando le proprietà di tale operazione. Partiremo dal semplice caso dell’intersezione di due soli insiemi, per poi estendere l’operazione al caso generale di più insiemi.

Al pari dell’unione, anche l’operazione di intersezione ha una grande importanza e ricorrerà molto spesso nel proseguimento dei vostri studi. Ad esempio, quando studieremo i sistemi di equazioni, vedremo che l’insieme delle soluzioni di un sistema è dato dall’intersezione tra gli insiemi delle soluzioni delle equazioni presenti nel sistema. Ma ci occuperemo di questi aspetti a suo tempo. 😉

Definizione di intersezione tra insiemi

Cominciamo con il fornire la definizione di intersezione tra insiemi, a partire dal semplice caso di due soli insiemi di partenza. L’operazione di intersezione tra insiemi fornisce come risultato un particolare insieme detto insieme intersezione degli insiemi di partenza.

Dati due insiemi {A} e {B}, l’insieme intersezione tra i due insiemi è dato da un insieme che contiene i soli elementi in comune tra i due insiemi {A} e {B}.

Di conseguenza, possiamo rappresentare l’insieme intersezione tra due insiemi {A} e {B} come:

A \cap B = \{x \: | \: x \in A \: \small{\text{e contemporaneamente} }\: x \in B \}

Al secondo membro abbiamo rappresentato l’insieme intersezione mediante la proprietà caratteristica.

In modo del tutto simile a quanto fatto per l’operazione di unione tra insiemi, possiamo provare a rappresentare l’operazione di intersezione tra insiemi in una forma più rigorosa. Cominciamo introducendo un insieme universo {E}, tale da essere un sovrainsieme di entrambi gli insiemi {A} e {B}. In altre parole, entrambi gli insiemi {A} e {B} sono dei sottoinsiemi dell’insieme universo {E}.

Possiamo allora scrivere:

A \cap B = \{x \in E \: | \: x \in A \: \small{\text{e contemporaneamente}} \: x \in B\}

A questo punto, osserviamo che l’espressione “e contemporaneamente” può essere sostituita con il simbolo “{\wedge}“. Per chi conosce la logica, precisiamo che tale simbolo si riferisce all’operazione di congiunzione logica (AND). Così abbiamo:

A \cap B = \left\{ x \in E \: | \:x \in A  \: \wedge \:  x \in B \right\}

Conviene fin da subito mostrare la rappresentazione attraverso i diagrammi di Venn dell’operazione di intersezione tra insiemi. Infatti, tale rappresentazione mostra in maniera chiara come è definita l’operazione stessa.

Consideriamo intanto i due insiemi:

A=\left\{ 1, 2, 3, 5,9 \right\}, \qquad B = \left\{ 1, 3,9,11,24\right\}

e fissiamo per essi un universo {E}. L’insieme intersezione è dato da:

A \cap B = \left\{ 1,3,9\right\}

Gli elementi {1, 3} e {9} sono infatti gli unici elementi in comune agli insiemi {A} e {B}. In altre parole, tali elementi hanno la proprietà di appartenere contemporaneamente ad entrambi gli insiemi {A} e {B}. Gli altri elementi appartengono invece soltanto ad uno dei due insiemi. Ad esempio, l’elemento {2} appartiene soltanto all’insieme {A} e di conseguenza non fa parte dell’insieme intersezione {A \cap B}.

Utilizzando i diagrammi di Venn possiamo rappresentare l’insieme intersezione tra gli insiemi {A} e {B} come segue:

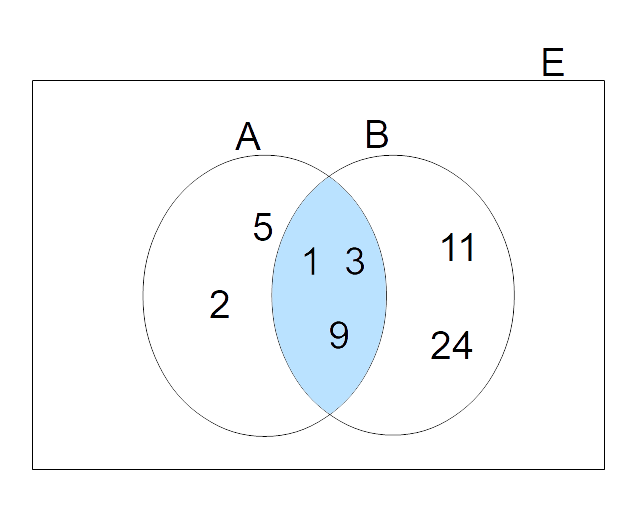
In azzurro è rappresentata la “parte in comune” tra i due insiemi, più propriamente la regione che contiene gli elementi in comune a tutti e due gli insiemi.

Forniamo ora ulteriori esempi sull’operazione di intersezione tra insiemi.

Esempi sull’intersezione tra insiemi

Esempio 1

Determinare l’intersezione (insieme intersezione) dei seguenti insiemi:

A=\left\{ 3,5,9,11\right\}, \quad B=\left\{ 4,12,9,3\right\}

Osserviamo che i due insiemi hanno in comune i soli elementi {3} e {9}. Di conseguenza abbiamo:

A \cap B = \left\{ 3, 9\right\}

Esempio 2

Determinare l’insieme intersezione dei seguenti insiemi:

A=\{x \in N \: | \: x < 10\}, \qquad B = \left\{ x \in \N \: | \: x=2n, \: n \in \N\right\}

Per non perderci, scriviamo anzitutto entrambi gli insiemi utilizzando la rappresentazione per elencazione. In questo modo, sarà tutto più semplice. 😉

L’insieme {A} è dato da tutti i numeri naturali inferiori a {10}, quindi:

A= \left\{ 0,1,2,3,4,5,6,7,8,9\right\}

L’insieme {B} è invece l’insieme di tutti i numeri naturali pari (un numero naturale pari {x} è esprimibile come il doppio di un certo numero naturale, da cui {x = 2n}, con {n} tale da essere un opportuno numero naturale ).

Ora, l’insieme {B} è infinito, e di conseguenza non possiamo rappresentarlo per elencazione riportandone tutti gli elementi. Tuttavia, aiutandoci con dei puntini possiamo scrivere i soli elementi che ci servono:

B=\left\{ 0,2,4,6,8,10, \dots\right\}

Nell’elencazione ci basta infatti arrivare ad un numero naturale maggiore o uguale all’elemento più grande dell’insieme {A}.

A questo punto non è troppo complicato determinare l’insieme intersezione dei due insiemi {A} e {B}:

A \cap B = \left\{ 0,2,4,6,8\right\}

Questi infatti sono gli unici elementi ad essere in comune tra i due insiemi dati.

Osserviamo infine che nonostante l’insieme {B} sia infinito, poiché l’insieme {A} è finito otteniamo come insieme intersezione un insieme finito.

Intersezione tra più di due insiemi

L’operazione di intersezione tra insiemi può essere estesa agevolmente al caso di tre o più insiemi.

L’insieme intersezione di tre o più insiemi è dato da un insieme che contiene gli elementi in comune a tutti gli insiemi di partenza. In simboli, fissato un insieme universo {E}: {\small A_1 \cap A_2 \cap A_3 \dots \cap A_n = \{x \in E \: | \: x \in A_1 \: \wedge \: x \in A_2 \: \dots \wedge\: x \in A_n \}, \:n \in \N}

Così ad esempio nel caso di tre insiemi in un dato universo {E} abbiamo:

A_1 \cap A_2 \cap A_3 = \{x \in E \: | \: x\in A_1 \: \wedge \: x \in A_2 \: \wedge \: x \in A_3 \}

Così l’insieme intersezione degli insiemi {A_1, \: A_2, \: A_3} è l’insieme che contiene tutti gli elementi in comune agli insiemi {A_1, \: A_2} e {A_3}.

Esempio

L’intersezione tra gli insiemi:

\small A=\left\{ 3,6,20,60\right\}, \qquad B=\left\{ 3,6,50\right\}, \qquad C=\left\{ 3,5,6,9,20,60\right\}

è data da:

A \cap B \cap C = \left\{3,6 \right\}

Gli elementi {3} e {6} sono infatti gli unici elementi in comune a tutti e tre gli insiemi.

Insiemi disgiunti

All’operazione di intersezione tra insiemi è legata un’importante definizione, ovvero quella di insiemi disgiunti.

Due o più insiemi si dicono disgiunti se il loro insieme intersezione è uguale all’insieme vuoto.

In altre parole, dati ad esempio due insiemi {A} e {B}, questi sono disgiunti se:

A \cap B = \emptyset

Proprietà dell’intersezione tra insiemi

Concludiamo la lezione presentando le proprietà dell’intersezione insiemistica.

Durante la lettura incontrerete il concetto di insieme complementare. Di questo ci occuperemo dettagliatamente in una successiva lezione, tuttavia per il momento sappiate che il complementare di un insieme {A} rispetto ad un dato insieme universo {E} è dato da tutti gli elementi dell’insieme {E} che non appartengono all’insieme {A}. In simboli:

\mathcal{C}_{E}A=\left\{ x \in E \: |x \not \in A\right\}

A parole, il complementare dell’insieme {A} rispetto all’universo {E} è un insieme i cui elementi appartengono all’insieme universo {E} e contemporaneamente non appartengono all’insieme {A}. Più brevemente, si tratta degli elementi dell’insieme {E} tali da non appartenere all’insieme {A}.

1) Intersezione tra un insieme e i suoi sottoinsiemi impropri

Dato un insieme {A}, i suoi sottoinsiemi impropri sono {A} stesso e l’insieme vuoto. Per le operazioni di intersezione tra l’insieme {A} e ciascuno dei suoi sottoinsiemi impropri abbiamo:

A \cap A =A

Infatti, gli elementi di {A} sono tutti elementi in comune con lo stesso insieme {A}. In altre parole, due insiemi uguali hanno tutti gli elementi in comune.

Inoltre:

A \cap \emptyset = \emptyset

Infatti, poiché l’insieme vuoto non contiene alcun elemento, esso non può avere alcun elemento in comune con nessun insieme. Di conseguenza, l’insieme intersezione è privo di elementi, e coincide con l’insieme vuoto.

2) Proprietà commutativa dell’intersezione

Si ha:

A \cap B = B \cap A 

3) Proprietà associativa dell’intersezione

A \cap (B \cap C) = (A \cap B) \cap C

4) Proprietà distributiva dell’intersezione rispetto all’unione

A \cap (B \cup C)=(A \cap B ) \cup (A \cap C)

Ricordiamo che il simbolo {\cup} si riferisce all’operazione di unione tra insiemi, che abbiamo visto nella precedente lezione.

5) Intersezione tra un insieme e il suo complementare

Fissato un universo {E}, abbiamo:

\mathcal{C}_EA \cap A = \emptyset

La proprietà discende dalla definizione di complementare di un insieme rispetto ad un fissato insieme universo.

Di conseguenza, un insieme e il suo complementare (rispetto ad un dato insieme universo) sono disgiunti.

6) Legge di De Morgan dell’intersezione (intersezione tra insiemi)

Abbiamo (legge di De Morgan dell’intersezione tra due insiemi):

\mathcal{C}_{E}(A \cap B) = \mathcal{C}_EA \cup \mathcal{C}_{E}B

Per chi già conosce la logica, la relazione appena scritta è la versione insiemistica della seguente legge della logica:

\neg(p \wedge q)=\neg p \vee \neg q 

ove {p} e {q} sono proposizioni logiche, “{\neg}” è il simbolo di negazione logica, “{\wedge}” è il simbolo della congiunzione logica (analoga dell’intersezione insiemistica), ed infine “{\vee}” è il simbolo della disgiunzione logica inclusiva (analoga dell’unione insiemistica).

7) Intersezione di un insieme con un suo sottoinsieme

Se {B \subseteq A}, abbiamo:

B \cap A = B

In altre parole, l’intersezione tra un insieme e un suo sottoinsieme restituisce l’insieme più piccolo dei due (il sottoinsieme).

Invece, con riferimento alla precedente lezione, l’unione tra un insieme {A} e un suo sottoinsieme {B} restituisce il sovrainsieme {A} (ovvero l’insieme più grande).

8) Intersezione di un insieme con l’insieme universo

Fissato un insieme universo {E} e dato un insieme {A} abbiamo:

A \cap E = A

Dato che per la definizione di insieme universo, abbiamo che {A \subseteq E}, la proprietà appena enunciata discende dalla {7}.

9) L’insieme intersezione è un sottoinsieme di ciascuno degli insiemi intersecati

Veniamo all’ultima proprietà sull’intersezione insiemistica che discutiamo in questa lezione. In particolare, vogliamo concludere mostrando che l’insieme che si ottiene come risultato dell’intersezione tra {A} e {B} è un sottoinsieme di entrambi gli insiemi di partenza.

Abbiamo:

A \cap B \subseteq A, \qquad A \cap B \subseteq B

Per questa lezione è tutto. Nella prossima lezione vedremo l’ultima operazione sugli insiemi che tratteremo in questo corso di lezioni, ovvero l’operazione di differenza tra insiemi. Buon proseguimento con SìMatematica! 🙂