La funzione radice cubica

 - 

Radicali

La funzione radice cubica è una particolare funzione che associa ad ogni numero reale il corrispondente valore che elevato al cubo restituisce il numero di partenza.

In questa lezione ci proponiamo di costruire la funzione radice cubica a partire dalla funzione cubica {y=x^3}, allo stesso modo con il quale abbiamo definito la funzione radice quadrata a partire dalla funzione {y=x^2}. Analizzeremo le più importanti proprietà della funzione radice cubica con particolare riferimento al grafico.

La funzione radice cubica a partire dalla funzione cubica y = x³

La funzione cubica {y=x^3} associa ad ogni numero reale il suo cubo. Tale funzione ha per dominio l’intero insieme dei numeri reali. Il codominio e l’insieme delle immagini della funzione coincidono e sono dati da tutto {\mathbb{R}}.

Il grafico di tale funzione cubica è il seguente:

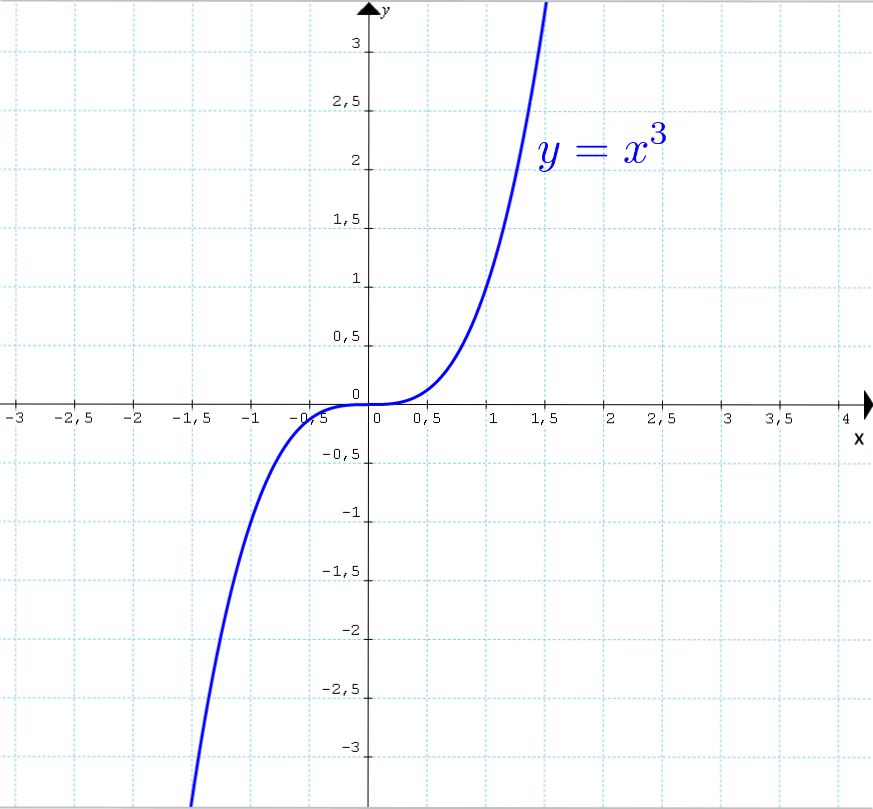
La funzione cubica {y=x^3} ha così la proprietà di essere sia iniettiva, sia suriettiva. Proviamo anzitutto la iniettività, ovvero:

f(x_1)=f(x_2) \quad \iff \quad x_1 = x_2

In altre parole una funzione è iniettiva se non assume mai lo stesso valore in punti diversi tra loro. Così avremo l’uguaglianza tra le valutazioni {f(x_1)} e {f(x_2)} soltanto se i due punti coincidono.

Ciò tra l’altro si traduce graficamente osservando che una funzione è iniettiva soltanto se tracciando una qualsiasi retta orizzontale questa interseca il grafico della funzione in un solo punto. E come è immediato verificare il grafico della funzione cubica {y=x^3} rispetta tale condizione.

Ma riprendiamo la verifica dell’iniettività dal punto di vista analitico. Nel caso della funzione cubica in esame si ha:

x_1 ^ 3 = x_2^3 \quad \iff \quad \sqrt[3]{x_1^3} = \sqrt[3]{x_2^3} \quad \iff \quad x_1 = x_2

Abbiamo quindi dimostrato l’iniettività della funzione cubica {y=x^3} estraendo la radice cubica di entrambi i membri dell’uguaglianza di partenza.

Per la suriettività, dobbiamo dimostrare che riusciamo sempre a trovare una controimmagine per ogni valore {y}. In altre parole, se la funzione è suriettiva, allora per ogni {y} esisterà sempre una {x} corrispondente tale che si abbia {x^3=y}.

E’ evidente che in questo caso riusciamo a trovare per ogni {y} reale la corrispondente {x}, espressa come:

x=\sqrt[3]{y}

Infatti considerando il grafico della funzione cubica {y=x^3}, preso un qualsiasi punto {y} nell’asse delle ordinate è sempre possibile trovare un unico punto {P} ad esso corrispondente e quindi determinare il valore della sua ascissa {x}.

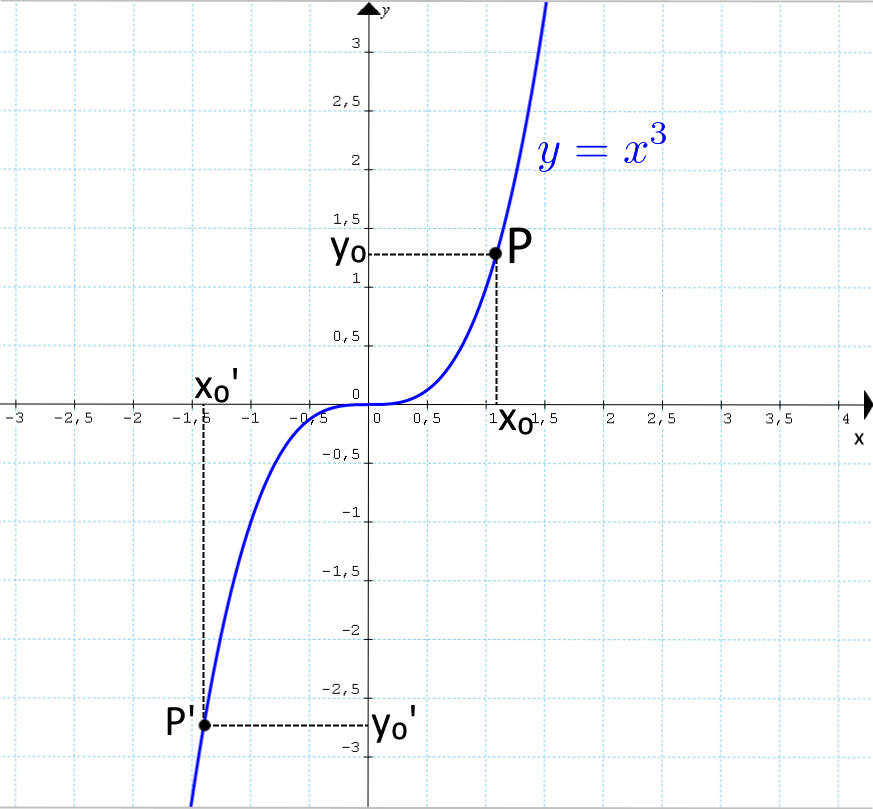
In conclusione la funzione cubica {y=x^3} è sia iniettiva, sia suriettiva. Di conseguenza è biiettiva (iniettiva più suriettiva) e quindi invertibile. In particolare, la funzione inversa di tale funzione cubica si chiama funzione radice cubica ed è così definita:

f:\mathbb{R} \rightarrow \mathbb{R} \: | \: x \rightarrow \sqrt[3]{x}

La funzione {f(x)=\sqrt[3]{x}} associa dunque ad ogni numero reale la sua radice cubica, ovvero quel numero reale che elevato alla terza potenza restituisce il numero reale di partenza.

Il grafico della funzione radice cubica si ottiene calcolando per ogni {x} la corrispondente radice cubica:

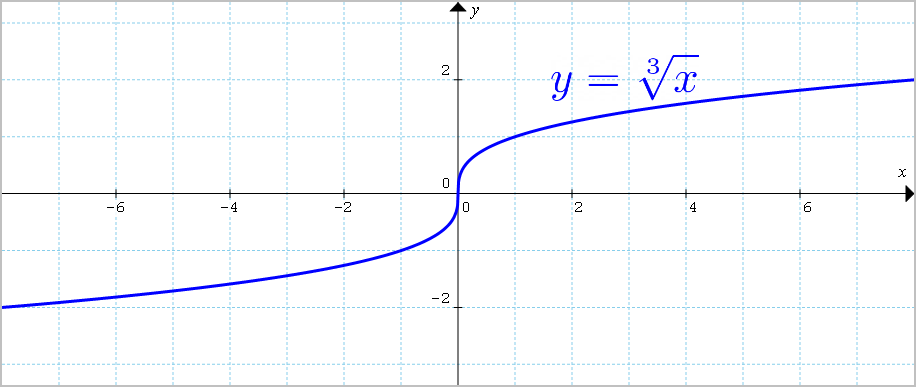
Osserviamo che il grafico è simmetrico rispetto all’origine. Infatti a valori opposti della {x} corrispondono valori opposti della {y}. Ad esempio:

\sqrt[3]{8}=2; \qquad \sqrt[3]{-8}=-2; 

In generale abbiamo quindi:

\sqrt[3]{x}=-\sqrt[3]{-x}

ovvero:

\boxed{\sqrt[3]{-x}=-\sqrt[3]{x}}

La proprietà è in generale valida per i soli radicali con indice dispari e consente di cambiare il segno del radicando a patto di porre un segno meno davanti al simbolo di radice. Così ad esempio:

\sqrt[3]{-27} = -\sqrt[3]{27}=-3

Facendo un ulteriore esempio con un radicando letterale:

\sqrt[5]{-x+7}=-\sqrt[5]{x-7}

In pratica ponendo un segno meno davanti al radicale abbiamo potuto sostituire il polinomio all’interno della radice con il polinomio ad esso opposto (abbiamo cioè cambiato i segni di tutti i suoi termini).

Attenzione: la proprietà non è invece valida nel caso dei radicali con indice pari. Infatti non è possibile estrarre la radice con indice pari di un numero negativo. E quindi in generale se esiste un radicale con indice pari avente per radicando un polinomio {P}, non potrà certamente esistere il radicale con indice pari avente per radicando l’opposto di quello stesso polinomio {-P}. E ciò conferma ulteriormente la non applicabilità della proprietà ai radicali con indice pari.

A conclusione della lezione, osserviamo che come nel caso della funzione radice quadrata, anche il grafico della funzione radice cubica presenta una simmetria con il grafico della funzione cubica {y=x^3} rispetto alla bisettrice del primo e terzo quadrante:

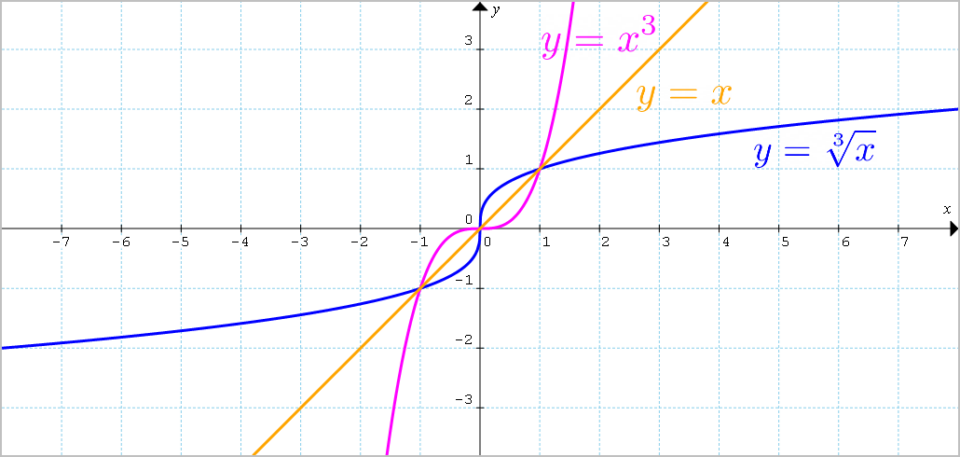
Ciò è diretta conseguenza del fatto che le due funzioni {y=\sqrt[3]{x}} e {y=x^3} sono una l’inversa dell’altra.

Per quanto riguarda la funzione radice cubica è tutto. Dalla prossima lezione torneremo ad occuparci del calcolo con i radicali ed in particolare vedremo la semplificazione dei radicali. Buon proseguimento!