La funzione radice quadrata

 - 

Radicali

La funzione radice quadrata è una particolare funzione che associa ad ogni numero reale non negativo un corrispondente valore anch’esso non negativo (quindi positivo o al più nullo). E il valore è tale che elevandolo al quadrato ritroviamo il numero reale di partenza.

Dopo aver introdotto la nozione di condizioni di esistenza per un radicale, procediamo introducendo la funzione radice quadrata e le sue più importanti proprietà. Il punto di partenza per definire tale funzione è dato dalla parabola di equazione {y=x^2}.

Fatte le dovute premesse vediamo subito la funzione radice quadrata e le sue principali proprietà, con particolare riferimento all’andamento del suo grafico.

La funzione radice quadrata a partire dalla parabola y=x²

Partiamo dal grafico della parabola {y=x^2}. Per disegnare il grafico basta associare ad ogni punto dell’asse {x} il valore {x^2}. In particolare, la funzione {y=x^2} ha per dominio l’intero insieme dei numeri reali, ed ha per insieme delle immagini i soli reali positivi (più lo zero).

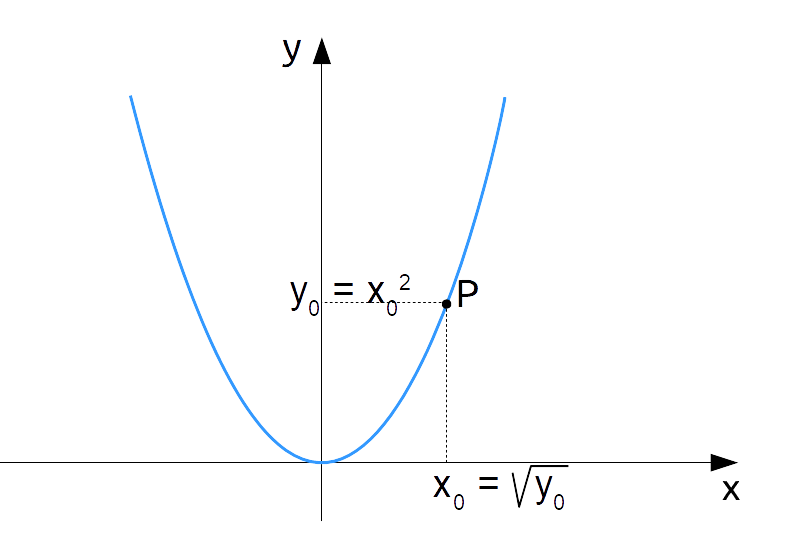
Il punto {P} della parabola ha coordinate {(x_0, \: y_0)}.

Osserviamo che al punto {x_0} dell’asse delle ascisse corrisponde il valore {y_0 = x_0^2} e viceversa al valore {y_0} corrisponde il punto {x_0 = \sqrt{y_0}} dell’asse delle ascisse. Ed è proprio il viceversa che a noi interessa. Il nostro obiettivo è infatti ricavare, a partire da un dato valore, un numero tale che il suo quadrato sia uguale al valore di partenza. E con ciò otterremo la funzione radice quadrata.

Tuttavia, è importante accorgersi che al valore {y_0} non corrisponde il solo punto {x_0} ma anche il punto {x_1}:

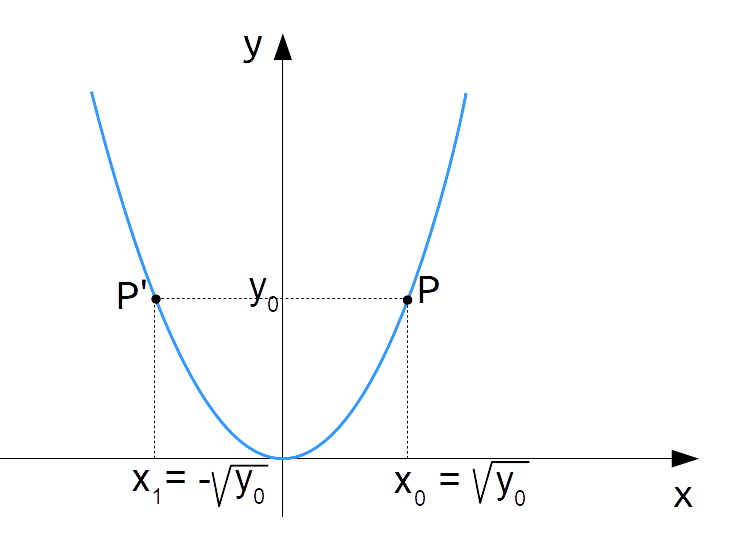
Di conseguenza, mentre a partire da un certo punto {x_0} otteniamo uno e un solo valore {y_0}, partendo dal valore {y_0} ad esso corrispondono due punti {x_0} e {x_1}. In altre parole, dato {y_0} i valori della {x} tali che {x^2 = y_0} sono due.

Ritroviamo così il discorso fatto a suo tempo: i valori della {x} tali da soddisfare ad esempio la condizione {x^2=25} sono {x_0 = 5} e {x_1 = -5}.

Tuttavia, osservando il grafico è immediato notare che, considerando ad esempio soltanto il primo quadrante, allora ad ogni valore {y_0} corrisponde uno ed un solo punto {x_0}. Così, restringendoci al solo primo quadrante, e quindi considerando le sole {x} positive (più lo zero), a partire da ciascun numero potremo determinare la sua radice quadrata, ottenendo una funzione. Infatti, avremo sempre uno ed un solo valore della radice quadrata.

Per costruire il grafico della funzione radice quadrata l’idea è quella di calcolare per ogni numero reale non negativo il corrispondente valore della radice quadrata. Escludiamo i numeri negativi poiché non esiste nessun numero che moltiplicato per sé stesso restituisce un risultato positivo. Non è quindi possibile estrarre la radice quadrata di un numero negativo.

Così ad esempio per {x=0} otteniamo come radice quadrata {y=0}. Infatti, {0^2=0}. Poi, per {x=\dfrac{1}{4}} otteniamo {y=\dfrac{1}{2}}. Infatti {\left( \dfrac{1}{2}\right)^2}=\dfrac{1}{4}. Procedendo in questo modo per un adeguato numero di punti otteniamo il grafico della funzione radice quadrata:

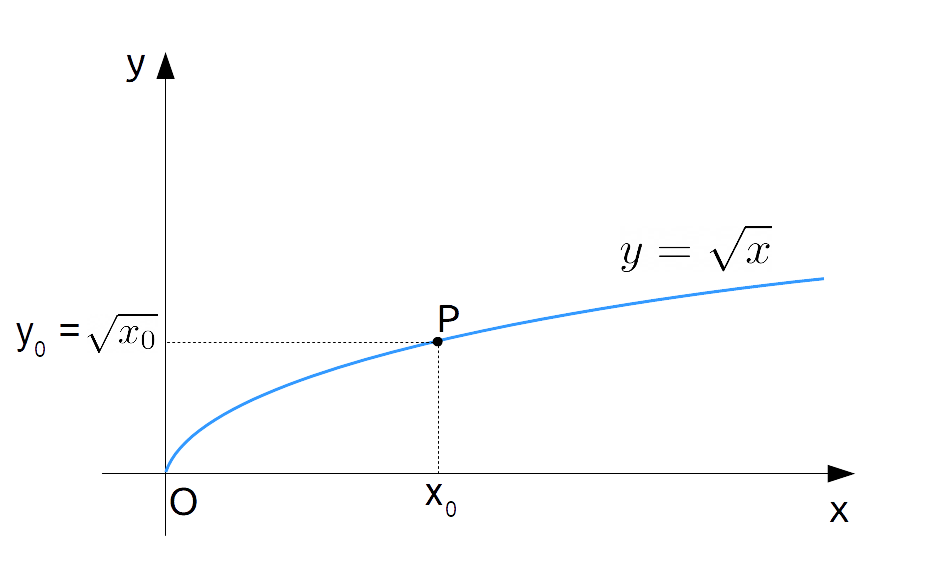
La funzione radice quadrata è in conclusione definita come:

f: \mathbb{R}^{+} \rightarrow \mathbb{R} \: | \: x \rightarrow \sqrt{x}

ovvero è una funzione avente per dominio i soli numeri reali positivi (più lo zero). Inoltre, la funzione è a valori reali (quindi il codominio è {\mathbb{R}}) ma il suo insieme delle immagini è dato dai soli reali positivi (più lo zero):

\Im (f)=[0, \: +\infty[

Tale insieme delle immagini è conseguenza del fatto di aver costruito la funzione radice quadrata a partire dalla funzione {y=x^2} restringendoci al solo primo quadrante. E quindi tutte le {x} positive (più lo zero) del grafico della parabola {y=x^2} rappresentano esattamente l’insieme delle immagini della funzione radice quadrata. E in particolare, avendo ristretto il dominio della funzione {y=x^2} ai soli reali positivi possiamo affermare che la funzione radice quadrata è l’inversa della funzione “quadrato di {x}“.

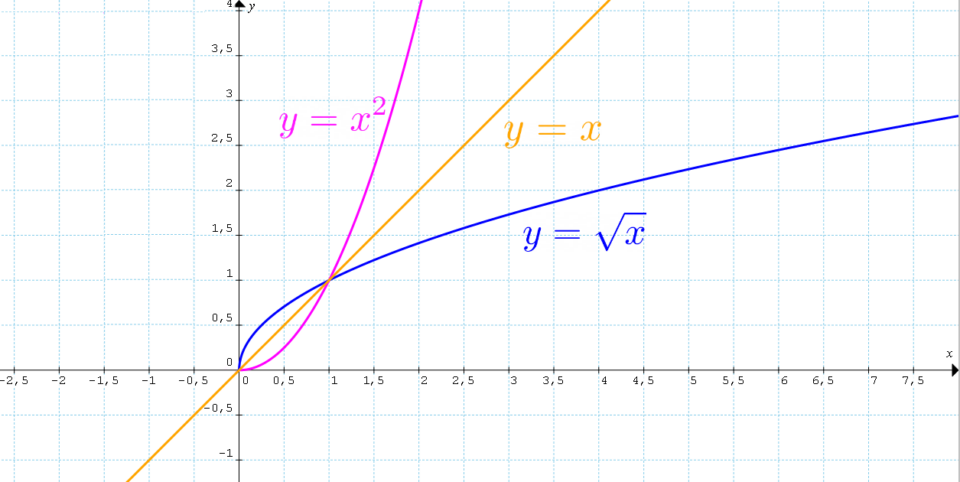
Osserviamo in particolare che il grafico della parabola {y=x^2} con dominio ristretto a {\mathbb{R}^{+ }} è simmetrico al grafico della funzione {y=\sqrt{x}} rispetto alla bisettrice del primo e terzo quadrante. Tale simmetria si verifica in generale per tutte le funzioni tra loro inverse.

Per quanto riguarda la funzione radice quadrata e le sue principali proprietà è tutto. Nella prossima lezione ci occuperemo della funzione radice cubica.