La partizione di un insieme è una collezione di insiemi ciascuno diverso dall’insieme vuoto, tali da essere a due a due disgiunti ed infine tali che la loro unione è uguale all’insieme di partenza.
Introduciamo così dopo aver visto le operazioni tra insiemi la definizione di partizione di un insieme. Si tratta di una insieme i cui elementi sono ancora degli insiemi, e questa è una caratteristica che presenta anche l’insieme potenza o insieme delle parti, del quale già ci siamo occupati. Tuttavia, prestiamo particolare attenzione al fatto che le definizioni di partizione di un insieme e di insieme delle parti fanno riferimento a due concetti completamente diversi.
Nel corso della lezione vedremo nel dettaglio la definizione di partizione di un insieme, la sua rappresentazione grafica con i diagrammi di Venn e presenteremo degli esempi sul suo utilizzo. Inoltre, vedremo in questo concetto quale ruolo gioca l’insieme complementare, visto nella precedente lezione.
Definizione di partizione di un insieme
Consideriamo un insieme {A} diverso dall’insieme vuoto per il quale sia stato definito un universo {E}. Sinteticamente, sia dato {A \neq \emptyset} con {A \subseteq E}.
Ora, un qualsiasi insieme formato da sottoinsiemi di {A} (o più propriamente, una qualsiasi collezione o famiglia di sottoinsiemi di {A}) rappresenta una partizione per l’insieme {A} se e solo se:
- ciascun sottoinsieme è diverso dal vuoto;
- i sottoinsiemi sono a due a due disgiunti. In altre parole, l’intersezione tra ciascuna possibile coppia di sottoinsiemi è uguale all’insieme vuoto;
- l’unione di tutti i sottoinsiemi ha come risultato l’insieme di partenza {A}.
Graficamente, è possibile rappresentare mediante i diagrammi di Venn una possibile partizione di un dato insieme {A} come segue:
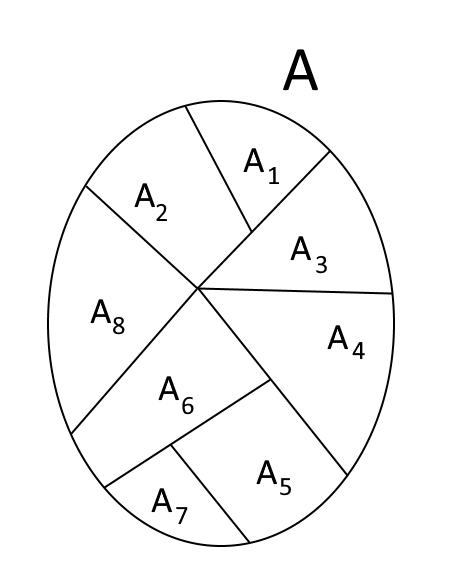
Intuitivamente l’idea è quella di immaginare la superficie del pavimento della nostra stanza suddivisa in tante piastrelle.
Ora, le proprietà che devono avere dei sottoinsiemi dell’insieme {A} affinché questi possano costituire una partizione di {A} possono essere espresse in simboli come segue:
\begin{align*} & A_i \neq \emptyset\\ \\ & A_i \cap A_j =\emptyset; \\ \\ & \cup_{i=1}^{n} A_i = A_1 \cup A_2 \cup \dots \cup A_n=A \end{align*}Queste non sono altro che le proprietà che fanno parte della definizione di partizione di un insieme ritradotte in linguaggio simbolico. Osserviamo che {n} indica il numero dei sottoinsiemi presenti.
Così, una possibile partizione di {A} si scriverà ad esempio come:
P(A)=\left\{ A_1, A_2\right\}se {A_1} e {A_2} sono dei sottoinsiemi di {A} tali da essere diversi dall’insieme vuoto, a due a due disgiunti e tali che la loro unione restituisce l’insieme {A}.
Attenzione. Per un dato insieme {A} esistono in generale più possibili partizioni. Precisiamo inoltre che ogni insieme ha almeno una partizione, data dall’insieme stesso.
Attenzione. Non confondiamo la simbologia {P(A)}, che indica una {\text{partizione}} di {A}, con la simbologia {\mathscr{P}(A)} che indica invece l’insieme delle parti di {A}.
Requisiti di un insieme affinché sia possibile determinare una partizione per esso
Come evidenziato nella definizione di partizione di un insieme {A}, l’insieme {A} deve essere diverso dall’insieme vuoto. In caso contrario, non è possibile determinare alcuna partizione per l’insieme stesso.
Ora, se l’insieme {A} ha un solo elemento, per esso è possibile scrivere un’unica partizione. Così ad esempio dato l’insieme:
A=\left\{ a\right\}formato da un solo elemento, esiste per esso un’unica partizione data dall’insieme {A}. Infatti, il sottoinsieme {A \subseteq A}:
- è diverso dall’insieme vuoto: {A \neq \emptyset};
- è disgiunto con sé stesso: {A \cap A = \emptyset};
- l’unione con sé stesso restituisce l’insieme {A}: {A \cup A = A}.
Per insiemi {A} dai due elementi in su abbiamo invece più possibili partizioni.
Esempi di partizioni di un insieme
Esempio 1
Consideriamo l’insieme:
A=\left\{ 1,2,3\right\}Abbiamo ad esempio:
P(A)=\left\{ \left\{ 1\right\}, \left\{ 2,3\right\}\right\}Verifichiamo tutti i requisiti di ciascun elemento di {P(A)}. Prima di tutto, osserviamo che ciascuno di essi è un sottoinsieme di {A}, come richiesto.
Abbiamo:
- ciascun sottoinsieme è diverso dall’insieme vuoto;
- i sottoinsiemi sono a due a due disgiunti. Infatti {\left\{1\right\} \cap \left\{2,3\right\} = \emptyset};
- l’unione dei sottoinsiemi restituisce l’insieme di partenza. Infatti {\left\{ 1\right\} \cup \left\{ 2,3\right\}=\left\{ 1,2,3\right\}=A}.
Osserviamo che {P(A)} non è l’unica partizione possibile per {A}. Infatti, un’altra è data da:
P_2(A)=\left\{ \left\{ 1,3\right\}, \left\{ 2\right\}\right\}A voi verificare che gli elementi di {P_2(A)} rispettano ancora i precedenti criteri.
Esempio 2
Dato l’insieme:
A=\left\{ 5,22,7,99,55\right\}scrivere {P(A)} in uno dei modi possibili.
Abbiamo:
P(A)=\left\{ \left\{ 5, 22\right\}, \left\{ 7,99\right\}, \left\{ 55\right\}\right\}Esempio 3
Scrivere una partizione dell’insieme:
A=\left\{ 5\right\}Poiché l’insieme ha un solo elemento, l’unica possibile partizione è quella banale, data dall’insieme stesso:
P(A)=\left\{ 5\right\}Insieme delle parti e partizione di un insieme
Consideriamo ancora l’insieme:
A=\left\{ 1,2,3\right\}L’insieme potenza di {A} (o insieme delle parti) è dato da:
\mathscr{P}(A)=\left\{ \emptyset, \{1\}, \{2\}, \left\{ 3\right\}, \left\{ 1,2\right\}, \left\{ 2,3\right\}, \left\{ 1,3\right\}, \left\{ 1,2,3\right\}\right\}Ora, le possibili partizioni di un insieme sono tutte sottoinsiemi dell’insieme potenza o insieme delle parti di {A}. In altre parole, una qualunque partizione di {A} avrà per elementi degli elementi dell’insieme potenza {\mathscr{P}(A)}.
Dunque, la costruzione di una partizione di {A} comincia dalla scelta dei suoi elementi all’interno dell’insieme potenza {\mathscr{P}(A)}.
Ad esempio, una partizione di {A} è in questo caso data da:
P(A)=\left\{ \left\{ 1\right\}, \left\{ 2,3\right\}\right\}e gli elementi {\left\{ 1\right\}} e {\left\{ 2,3\right\}} sono dei sottoinsiemi di {A} che appartengono anche all’insieme delle parti {\mathscr{P}(A)}.
Questa è dunque la differenza tra l’insieme delle parti o insieme potenza di {A} e una partizione di {A}. Gli elementi dell’insieme delle parti di {A}, ovvero gli elementi di {\mathscr{P}(A)}, sono tutti i sottoinsiemi di {A} e quindi dei possibili candidati ad essere elementi di una partizione di {A}.
In altri termini, l’insieme delle parti {A} contiene dei mattoni con i quali è possibile costruire una partizione dell’insieme {A}. In ogni caso, l’insieme delle parti contiene anche l’insieme vuoto, ma questo non potrà mai essere un elemento di nessuna partizione di {A}.
Un dato insieme e il suo complementare come partizione del loro insieme universo
Fissato un universo {E} per un insieme {A} non vuoto, una partizione per l’insieme universo {E} è data da:
P(A)=\left\{ \left\{ \mathcal{C}_EA, A\right\}\right\}Ovvero, un insieme {A} e il suo complementare rispetto all’universo {E} costituiscono una partizione per l’insieme {E}.
Infatti, l’insieme {A} e il suo complementare sono entrambi diversi dall’insieme vuoto, la loro intersezione dà come risultato l’insieme vuoto e la loro unione restituisce l’insieme {E}.
Partizioni di insiemi infiniti
Se un insieme è finito ed è costituito da {n} elementi, con {n > 1}, per esso sono possibili più partizioni. Il numero esatto delle partizioni dipende da {n}, ma per i nostri fini evitiamo di presentare la regola per determinare tale numero.
Se invece un insieme è infinito, allora le partizioni che si possono costruire per esso sono infinite.
Dato ad esempio l’insieme dei numeri naturali, una delle possibili infinite partizioni per esso è:
P(\N)=\left\{ \left\{x \in \N \: | \: x < 50\right\}, \left\{ x \in \N \: | \: x \geq 50\right\}\right\}Osserviamo che i sottoinsiemi che costituiscono la partizione rispettano tutti i requisiti ormai noti. In particolare, la loro intersezione è uguale all’insieme vuoto, poiché l’elemento {50} è escluso dal primo sottoinsieme ma è compreso nel secondo.
Osserviamo che il seguente insiemi di insiemi non è una partizione per l’insieme dei numeri naturali:
\left\{ \left\{ x \in \N \: | \: x < 50\right\}, \left\{ x \in \N \: | \:x > 50\right\}\right\}Infatti i due insiemi sono ancora disgiunti, ma l’elemento {50} viene escluso da entrambi gli insiemi. Di conseguenza, l’unione degli insiemi non restituisce l’insieme {\N} di partenza.
Anche il seguente insieme di insiemi non costituisce una partizione di {\N}:
\left\{ \left\{ x \in \N \: | \: x \leq 50\right\}, \left\{ x \in \N \: | \:x \geq 50\right\}\right\}Infatti, i due insiemi hanno in comune l’elemento {50}, e quindi non rispettano il criterio di dover essere disgiunti.
Nel proseguimento dei vostri studi non sarà infrequente dover suddividere un insieme in più sottoinsiemi in modo da ottenere una partizione. Occorrerà in questi casi sempre tener conto degli accorgimenti evidenziati negli esempi.
Per questa lezione è tutto. Nella prossima lezione ci occuperemo del prodotto cartesiano.
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
