Punto medio di un segmento sulla retta

 - 

Coordinate cartesiane e retta nel piano

Fissata come sistema di riferimento una retta r, il punto medio di un segmento giacente sulla stessa retta r ed avente per estremi i punti A di ascissa a e B di ascissa b è il punto M avente come ascissa la media aritmetica delle ascisse degli estremi del segmento AB. In altre parole, indicata con m l’ascissa del punto medio M, si ha m = (a + b)/2.

Dopo aver introdotto nella precedente lezione un particolare sistema di riferimento cartesiano dato da una retta r, proseguiamo introducendo la nozione di punto medio di un segmento relativo alla stessa retta r. Così, quello che ci proponiamo è individuare l’ascissa del punto medio di un segmento i cui punti sono tutti appartenenti ad una data retta r, che utilizziamo come riferimento. In questo modo, le ascisse di ciascun punto del segmento saranno delle opportune coordinate cartesiane sulla retta r.

Così, quello che facciamo è utilizzare la retta r come spazio unidimensionale, nel quale possiamo in generale avere punti, segmenti e semirette. In tale spazio abbiamo cioè una sola dimensione, poiché infatti ciascun punto è univocamente individuato nella retta r mediante un unico numero, detto ascissa.

Vedremo più avanti come sia anche possibile lavorare in uno spazio bidimensionale (detto più comunemente piano). In tal caso, ciascun punto del piano sarà individuato da due coordinate cartesiane, dette rispettivamente ascissa ed ordinata. Utilizzeremo in particolare un sistema di riferimento non più dato da una sola retta ma bensì da due rette, dette assi cartesiani.

Ma rimaniamo per ora nel nostro sistema di riferimento dato dalla sola retta r, e vediamo nel dettaglio come determinare l’ascissa del punto medio di un segmento giacente sulla retta r.

Come calcolare l’ascissa del punto medio di un segmento sulla retta r

Consideriamo un sistema di riferimento dato da una retta {r}. Un tale sistema di riferimento è unidimensionale poiché ciascun punto sulla retta {r} può essere individuato da un solo numero, detto ascissa.

Consideriamo un segmento {\overline{AB}} giacente sulla retta {r}, i cui estremi sono i punti {A=(a)} e {B=(b)} (oppure {A(a)} e {B(b)}, in base alle notazioni utilizzate).

Per definizione, il punto medio {M=(m)} del segmento {\overline{AB}} è tale da rispettare l’uguaglianza:

AM=MB

In altre parole, il punto {M} è un punto tale che le lunghezze algebriche dei segmenti {\overline{AM}} e {\overline{MB}} sono tra loro uguali.

Ma tenendo conto della definizione di lunghezza algebrica di un segmento data nella precedente lezione, l’uguaglianza appena scritta diviene:

m-a=b-m

Da cui ricavando {m}:

2m=b+a \quad \Rightarrow \quad \boxed{m=\dfrac{a+b}{2}}

Abbiamo così la seguente definizione.

Il punto medio di un segmento {\overline{AB}} sul riferimento dato da una retta r ha ascissa {m} data da:{m=\dfrac{a+b}{2}}che rappresenta la media aritmetica delle ascisse degli estremi del segmento {\overline{AB}}.

Osservazione. Ricordiamo che la lunghezza algebrica di un segmento sulla retta {r} è data dalla differenza tra l’ascissa del secondo estremo e l’ascissa del primo estremo. Così ad esempio la lunghezza algebrica del segmento {\overline{AB}} è data da {b-a}, con {a, \: b} ascisse rispettivamente degli estremi {A} e {B}.

Come esprimere l’ascissa di un generico punto appartenente al segmento {\overline{AB}}

Per quanto detto sinora, dato un segmento {\overline{AB }} giacente su una retta {r} presa come riferimento, possiamo scrivere le ascisse di tre suoi punti:

A=(a), \quad  M=\left( \dfrac{a+b}{2}\right), \quad  B=(b)

Il problema che ora vogliamo risolvere è quello di poter scrivere un’espressione per l’ascissa {x} di un generico punto {P} appartenente al segmento {\overline{AB}}.

Osserviamo che l’ascissa del punto medio {M} può essere riscritta, applicando la proprietà distributiva della divisione, come segue:

m=\dfrac{1}{2}a+\dfrac{1}{2}b

In generale, l’ascissa {x} di un generico punto {P} appartenente al segmento {\overline{AB}} avrà espressione:

x=\alpha \cdot a + \beta \cdot b

ove {a} e {b} sono le ascisse degli estremi del segmento e {\alpha} e {\beta} sono dei numeri reali non negativi e tali che {\alpha + \beta = 1}.

Effettivamente, per {\alpha=1} e {\beta = 0} otteniamo l’ascissa del primo estremo del segmento:

x=1 \cdot a + 0 \cdot b = a

mentre per {\alpha= 0 } e {\beta = 1} otteniamo l’ascissa del secondo estremo del segmento:

x=0 \cdot a + 1 \cdot b = b

Effettivamente, poi, in entrambi i casi abbiamo {\alpha + \beta = 1}.

Così l’ascissa {m} del punto medio {M} del segmento {\overline{AB}} si può ottenere a partire dall’espressione dell’ascissa {x} del generico punto {P} del segmento {\overline{AB}} ponendo {\alpha = 1/2} e {\beta =1/2}. Ed osserviamo che anche in questo caso abbiamo:

\alpha + \beta = \dfrac{1}{2}+\dfrac{1}{2}=1

Ora, osserviamo che poiché {\alpha+\beta=1} allora dovrà necessariamente essere, esplicitando ad esempio {\alpha}:

\alpha= 1-\beta

Osservazione. Si è qui scelto di ricavare {\alpha} e non {\beta} poiché in questo modo, come vedremo nel seguito, sarà possibile ottenere ordinatamente i punti del segmento {\overline{AB}} al crescere di {\beta}. L’avverbio “ordinatamente” si riferisce al verso positivo stabilito nella retta {r}.

Così sostituendo a {\alpha} l’espressione {1-\beta} possiamo esprimere l’ascissa {x} del generico punto {P} del segmento {\overline{AB}} come:

\boxed{x=(1-\beta) \cdot a + \beta  \cdot b, \qquad 0 \leq  \beta \leq 1 } \qquad (*)

Abbiamo così scritto l’equazione parametrica del segmento {\overline{AB}} sul riferimento dato dalla retta {r}, equazione che fornisce il valore dell’ascissa di ogni punto del segmento {\overline{AB}} in corrispondenza di ciascun valore del parametro {\beta} compreso tra {0} e {1}.

Per completezza, dimostriamo che la relazione è valida per ogni {\beta} compreso tra {0} e {1} (inclusi i valori {0} e {1}).

Il nostro obiettivo è allora dimostrare che per ogni {\beta} tale che {0 \leq \beta \leq 1} la formula * restituisce un valore per l’ascissa {x} sempre compreso tra {a} e {b} (inclusi {a} e {b}). Una volta dimostrato questo possiamo affermare che la * restituisce l’ascissa di un generico punto del segmento {\overline{AB}}.

Quindi, dobbiamo dimostrare che:

a\leq  \overbrace{(1- \beta)  \cdot a + \beta  \cdot b}^{x} \leq b

Cioè equivale a dimostrare che valgano contemporaneamente le seguenti disuguaglianze:

\begin{align} & (1-\beta)\cdot a + \beta \cdot b \geq a, \\ &(1-\beta)\cdot a + \beta  \cdot b \leq b\end{align}

Cominciamo dalla 1, e sottraiamo l’ascissa {a} del punto {A} ad entrambi i membri:

(1-\beta) \cdot a + \beta \cdot b - a \geq a-a 

ovvero:

\begin{align*} &\cancel{a}-\beta \cdot a +\beta \cdot b -\cancel{a} \geq 0, \\ \\ &\beta (-a+b) \geq 0\end{align*}

L’ultima relazione scritta è vera poiché {\beta } è per definizione non negativo, ed inoltre la somma algebrica {-a+b}, che può essere riscritta come la differenza {b-a}, è positiva in quanto per ipotesi {b > a} (infatti il punto {B} segue nella retta {r} il punto {A}). Così la condizione 1 è verificata.

In modo del tutto simile possiamo dimostrare che anche la condizione 2 è verificata. Basta infatti sottrarre {b} membro a membro e procedere con opportuni raccoglimenti:

\begin{align*} & (1-\beta)\cdot a + \beta  \cdot b-b \leq b -b, \\ \\ &  a-\beta \cdot a +\beta \cdot b - b \leq 0, \\ \\ &a(1-\beta)-b(-\beta+ 1) \leq 0,  \\ \\ &(1-\beta) (a-b) \leq 0\end{align*}

La relazione appena scritta è verificata poiché {1-\beta} è una quantità sempre non negativa, mentre la quantità {a-b} è negativa (infatti, il punto {B} segue nella retta {r} il punto {A}).

Dunque la relazione * risulta verificata per {0 \leq \beta \leq 1} ed effettivamente restituisce l’ascissa di un punto del segmento {\overline{AB}} sulla retta {r} per ogni valore di {\beta}. Quindi in conclusione la * rappresenta l’equazione parametrica del segmento {\overline{AB}} nel riferimento cartesiano unidimensionale {r}.

Esempi (ascissa del punto medio di un segmento)

Esempio 1

Dati i punti {A=(-2)} e {B=(4)} determinare il punto medio {M} del segmento {\overline{AB}}, il punto medio del segmento {\overline{AM}} e il punto medio del segmento {\overline{BM}}. Utilizzare come sistema di riferimento una retta {r}.

Indichiamo con {a=-2} l’ascissa del punto {A} e con {b=4} l’ascissa del punto {B}. Per l’ascissa {m} del punto medio {M} del segmento {\overline{AB}} abbiamo:

m=\dfrac{a+b}{2}=\dfrac{-2+4}{2}=1

Allo stesso modo, per l’ascissa {m_1} di {M_1}, punto medio del segmento {\overline{AM}} abbiamo:

m_1 = \dfrac{a+m}{2}=\dfrac{-2+1}{2}=-\dfrac{1}{2}

Infine, per l’ascissa {m_2} di {M_2}, punto medio del segmento {\overline{MB}}:

m_2= \dfrac{m+b}{2}=\dfrac{1+4}{2}=\dfrac{5}{2}

Possiamo rappresentare i punti calcolati sulla retta {r} come segue:

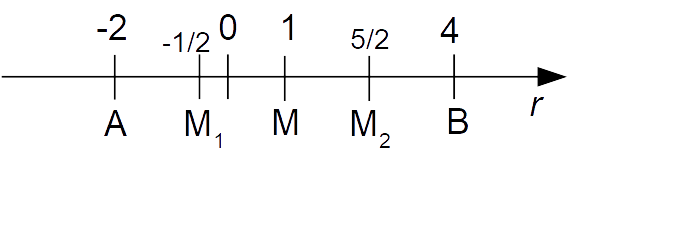
Osserviamo infine che a partire dalla relazione *, l’ascissa del punto {M} si ottiene per {\beta=\dfrac{1}{2}}, quella del punto {M_1} si ottiene per {\beta=\dfrac{1}{4}} e infine l’ascissa del punto {M_2} si ottiene per {\beta=\dfrac{3}{4}}. Infatti:

\begin{align*} &m=(1-\beta) a + \beta b = \left( 1-\dfrac{1}{2}\right) \cdot (-2)+\dfrac{1}{2} \cdot 4=1, \\ \\ & m_1 = (1-\beta)a+\beta b = \left( 1-\dfrac{1}{4}\right) \cdot (-2)+\dfrac{1}{4} \cdot 4=-\dfrac{1}{2}, \\ \\ & m_2 = (1-\beta)a+\beta b = \left( 1-\dfrac{3}{4}\right)\cdot(-2)+\dfrac{3}{4} \cdot 4= \dfrac{5}{2} \end{align*}

I valori di {\beta} scelti si giustificano osservando che esiste una relazione di diretta proporzionalità tra il valore di {\beta} corrispondente ad un certo punto {P} e la lunghezza {|AP|} del segmento {\overline{AP}}, avente per estremi il punto {A=(a)} e il punto {P=(x)}. E in ogni caso, ad esempio per ricavare il valore di {\beta} corrispondente al punto {M} basta sostituire la sua ascissa {m} nella *, ricavando {\beta}:

\small \begin{align*} & m=(1-\beta)a+\beta b \quad \Rightarrow \quad m=a-\beta a+\beta b \\ \\ &\Rightarrow m-a=\beta(-a+b) \quad \Rightarrow \quad \beta = \dfrac{m-a}{-a+b}= \dfrac{1-(-2)}{-(-2)+4}=\dfrac{1}{2}\end{align*}

il che conferma che l’ascissa del punto {M} si ottiene per {\beta = \dfrac{1}{2}}.

Le osservazioni fatte sui valori del parametro {\beta} corrispondenti ai punti {M, \: M_1, \: M_2} hanno una loro importanza. Infatti, ciò mette in evidenza che grazie alla proprietà di continuità della retta, ad ogni valore dell’ascissa {x} di un punto {P} sulla retta {r} corrisponde un suo proprio valore del parametro {\beta}. Ovvero, per ogni punto {P} preso sulla retta {r} esiste un valore di {\beta} compreso tra {0} e {1} inclusi, tale che la * restituisce l’ascissa {x} dello stesso punto {P}.

Conclusioni

Per quanto riguarda questa lezione sul punto medio di un segmento sulla retta r è tutto. Nella prossima lezione introdurremo la nozione di distanza tra due punti della retta r. Buon proseguimento!