Regola di Cartesio

 - 

Equazioni (superiori)

Passiamo ora ad esaminare una regola per le equazioni di secondo grado: la regola di Cartesio. Tale regola permette di determinare il segno delle soluzioni di un’equazione di secondo grado senza risolvere l’equazione. L’ipotesi sulla quale si basa la regola è che l’equazione abbia discriminante maggiore o uguale a zero. Questa è infatti la condizione necessaria per l’esistenza delle soluzioni reali di un’equazione di secondo grado.

La regola di Cartesio mette in relazione i segni dei coefficienti di un’equazione di secondo grado con i segni delle sue soluzioni. Ed è proprio sulla base di tale ragionamento che è possibile “predire” il segno delle soluzioni senza calcolarle.

Per curiosità, precisiamo che la regola di Cartesio si estende anche al caso di equazioni di grado superiore al secondo. Tuttavia, considereremo in questa lezione il solo caso relativo ad equazioni di secondo grado.

NOTA: nel paragrafo a seguire introduciamo in modo ragionato la regola di Cartesio fornendone la dimostrazione. Per chi vuole passare direttamente allo studio della regola a livello pratico, è possibile passare subito al relativo paragrafo. Consigliamo comunque di leggere tutta la lezione, poiché comprendere il ragionamento alla base della regola di Cartesio è una valida palestra per comprendere i ragionamenti sulle dimostrazioni.

Introduzione alla regola di Cartesio: relazione tra i segni dei coefficienti e i segni delle soluzioni

Consideriamo l’equazione di secondo grado in forma normale:

ax^2+bx+c = 0

Supponiamo che l’equazione ammetta soluzioni reali, ovvero che si abbia {\Delta = b^2-4ac \geq 0}.

Ipotizziamo di non essere interessati alle soluzioni dell’equazione, ma soltanto ai segni delle soluzioni stesse. In questo caso, è possibile dedurre i segni delle soluzioni a partire dai segni dei coefficienti.

Un principio fondamentale sul quale si basa la regola di Cartesio è dato dal fatto che il prodotto tra due numeri è negativo se e solo se i due numeri sono discordi. Viceversa, se il prodotto tra due numeri è positivo i due numeri sono concordi.

In parole più semplici, se il prodotto tra due numeri è positivo, questi hanno lo stesso segno. Se invece il segno del prodotto è negativo, i due numeri hanno segno diverso l’uno dall’altro.

Ora, come visto nella precedente lezione, sappiamo che il prodotto delle soluzioni di un’equazione di secondo grado si esprime come:

p=\dfrac{c}{a}

Così il prodotto delle soluzioni di un’equazione di secondo grado è positivo se i coefficienti a, c sono concordi (ovvero hanno lo stesso segno). E quindi se detti coefficienti sono concordi le soluzioni dell’equazione saranno anch’esse concordi (infatti il loro prodotto è positivo).

Ora, la somma delle soluzioni di un’equazione di secondo grado è data da:

s=-\dfrac{b}{a}

Così la somma delle soluzioni sarà positiva se i coefficienti a, b sono discordi. Se invece tali coefficienti sono concordi la somma delle soluzioni sarà negativa.

Nel caso di soluzioni di segno differente, possiamo inoltre affermare che:

• se la somma (algebrica) delle soluzioni dell’equazione è negativa, la soluzione con valore assoluto maggiore è negativa;
• invece, se la somma (algebrica) delle soluzioni dell’equazione è positiva, la soluzione con valore assoluto maggiore è positiva.

Tali affermazioni si giustificano osservando che se due numeri {m} e {n} hanno segno differente, la loro somma sarà negativa solo se il valore assoluto del numero negativo è più grande del numero positivo. Viceversa, la loro somma sarà positiva se il numero positivo è più grande del valore assoluto del numero negativo. Basta fare dei piccoli esperimenti con dei valori numerici per convincersene. 😉

A questo punto, mettiamo insieme le informazioni relative alla somma e al prodotto delle soluzioni e ai segni dei coefficienti dell’equazione di partenza e cerchiamo di trarre delle conclusioni sui segni delle soluzioni, analizzando i possibili casi.

In particolare, i casi possibili sono:

• coefficienti dell’equazione tutti dello stesso segno;
• {a} e {c} concordi, {a} e {b} discordi;
• coefficienti {a} e {c} discordi, coefficienti {a} e {b} concordi;
• infine, {a} e {c} discordi, {a} e {b} discordi.

Primo caso: coefficienti dell’equazione tutti dello stesso segno

Se i coefficienti {a} e {c} sono concordi, le soluzioni sono concordi (prodotto delle soluzioni positivo). E se inoltre i coefficienti {a} e {b} sono concordi, la somma delle soluzioni è negativa.

Ma in generale, affinché la somma tra due numeri sia negativa almeno uno dei due numeri dovrà essere negativo. E dato che già sappiamo che le soluzioni sono concordi, dovranno necessariamente essere entrambe negative. Quindi, se tutti i coefficienti dell’equazione hanno lo stesso segno, le soluzioni dell’equazione sono entrambe negative.

Secondo caso: coefficienti a e c concordi, coefficienti a e b discordi

Supponiamo che i coefficienti {a} e {c} siano concordi (prodotto delle soluzioni positivo), e i coefficienti {a} e {b} siano discordi (somma delle soluzioni positiva). In tal caso, le soluzioni hanno lo stesso segno e affinché la loro somma sia positiva devono necessariamente essere entrambe positive. Infatti affinché una somma tra due numeri sconosciuti risulti sempre positiva è necessario che entrambi i numeri siano positivi.

Terzo caso: coefficienti a e c discordi, coefficienti a e b concordi

Se i coefficienti {a} e {c} sono discordi, il prodotto delle soluzioni è negativo e quindi le soluzioni hanno segno differente.

In particolare, dato che i coefficienti {a} e {b} sono concordi, la somma delle soluzioni è negativa e di conseguenza la soluzione con valore assoluto maggiore è quella negativa.

Quarto caso: coefficienti a e c discordi, coefficienti a e b discordi

In quest’ultimo caso, il prodotto delle soluzioni è negativo e la loro somma è positiva. Allora le due soluzioni avranno segno differente e la soluzione di valore assoluto maggiore sarà quella positiva.

Abbiamo così già ottenuto le regole che ci servono per poter determinare i segni delle soluzioni di un’equazione di secondo grado a partire dai segni dei suoi coefficienti. Rimane soltanto da rileggerle in una maniera più intuitiva.

Regola di Cartesio: permanenze e variazioni in un’equazione di secondo grado

Per riassumere le regole appena stabilite in modo pratico, riprendiamo la forma generale di un’equazione di secondo grado in forma normale:

ax^2+bx+c=0

Osserviamo che nella forma normale i termini sono ordinati per grado della x decrescente. Di conseguenza ritroveremo i coefficienti esattamente nell’ordine {a, \: b, \: c}.

Leggendo i coefficienti dell’equazione da sinistra a destra, diciamo che abbiamo:

• una variazione, ogni volta che il segno di un coefficiente è differente dal segno del coefficiente che lo precede;
• una permanenza, ogni volta che il segno di un coefficiente è uguale al segno del coefficiente che lo precede.

Così ad esempio nell’equazione:

3x^2-5x+2=0

abbiamo due variazioni. Infatti, passando dal coefficiente {a} al coefficiente {b} abbiamo una variazione di segno (infatti il segno del coefficiente {a} è positivo mentre il segno del coefficiente {b} è negativo). Allo stesso modo, anche passando dal coefficiente {b} al coefficiente {c} abbiamo una variazione (infatti, mentre il segno del coefficiente {b} è negativo, il segno del coefficiente {c} è positivo).

Invece, nell’equazione:

3x^2-5x-2=0

abbiamo una variazione e una permanenza. Infatti, il coefficiente {a} è positivo e il coefficiente {b} è negativo (variazione), mentre il coefficiente {c} ha lo stesso segno del coefficiente {b} (permanenza).

Ora, a cosa ci servono le variazioni e le permanenze? Tali concetti permettono di stabilire una comoda regola pratica che consente di determinare il segno delle soluzioni di un’equazione di secondo grado (regola di Cartesio).

Riprendiamo le precedenti casistiche sui segni dei coefficienti. In particolare, costruiamo una tabella che indica i i possibili segni dei coefficienti relativi a ciascuna casistica. Inoltre, per ciascuna casistica indichiamo le variazioni e le permanenze.

Regola di Cartesio (equazioni di secondo grado)

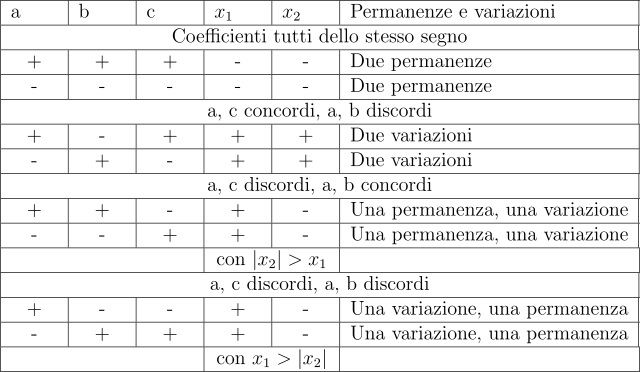
Possiamo a questo punto enunciare la Regola di Cartesio.

Regola di Cartesio. Ipotizziamo che un’equazione di secondo grado abbia soluzioni reali.
Considerata allora detta equazione nella forma normale {ax^2+bx+c=0}, possiamo affermare che ad ogni variazione corrisponde una soluzione positiva, e ad ogni permanenza corrisponde una soluzione negativa.
Infine, nel caso di soluzioni di segno differente tra loro, se abbiamo prima una permanenza e poi una variazione, la soluzione negativa ha valore assoluto maggiore della soluzione positiva. Invece, se abbiamo prima una variazione e poi una permanenza la soluzione positiva è maggiore del valore assoluto della soluzione negativa.

Vediamo ora degli esempi sull’utilizzo della regola di Cartesio.

Esempio 1

Mediante la regola di Cartesio determinare i segni delle soluzioni dell’equazione:

x^2+2x-35=0

L’equazione si presenta già in forma normale. Vediamo il determinante:

\Delta = b^2-4ac=2^2-4 \cdot 1 \cdot (-35 )= 4+140=144 > 0

Il determinante è maggiore di zero per cui l’equazione ha due soluzioni reali e coincidenti. Ora cerchiamo di capirne il segno.

Controlliamo i segni dei coefficienti nell’ordine da sinistra verso destra. Poiché i segni di {a} e {b} sono entrambi positivi, abbiamo una permanenza. Inoltre poiché il segno di {c} è diverso da {b} abbiamo una variazione.

Nell’ordine abbiamo una permanenza seguita da una variazione. Di conseguenza la soluzioni sono di segno differente e la soluzione negativa è in modulo maggiore della soluzione positiva.

Infatti utilizzando la formula risolutiva otteniamo per l’equazione le soluzioni:

x_1=-7; \qquad x_2 = 5

Le due soluzioni come ci aspettavamo sono discordi e il valore assoluto della soluzione negativa è maggiore della soluzione positiva. Infatti {|-7|>5}.

Esempio 2

Mediante la regola di Cartesio determinare i segni delle soluzioni dell’equazione:

6x^2+29x+28=0

L’equazione è già in forma normale. Per il determinante:

\Delta=b^2-4ac=29^2-4 \cdot 6 \cdot 28 = 841-672=169>0

Essendo {\Delta > 0} abbiamo per l’equazione due soluzioni reali e distinte.

Per il loro segno, osserviamo che nell’equazione abbiamo due permanenze. Infatti i segni dei coefficienti sono tutti uguali. Di conseguenza le due soluzioni saranno negative.

Infatti, risolvendo l’equazione otteniamo:

x_1= -\dfrac{7}{2}; \qquad x_2 = -\dfrac{4}{3}

Utilità della regola di Cartesio

La regola di Cartesio è sicuramente utile per controllare la correttezza delle equazioni di secondo grado. Se infatti le soluzioni che abbiamo calcolato hanno dei segni tali da non rispettare la regola di Cartesio, sicuramente abbiamo commesso un errore.

Inoltre, è possibile determinare facilmente il segno delle soluzioni ottenute, senza l’uso della calcolatrice, anche in quei casi ove non sia immediato stabilire il segno delle soluzioni stesse. Pensiamo ad esempio a quei casi ove otteniamo delle soluzioni contenenti termini anche irrazionali.

Consideriamo ad esempio l’equazione:

x^2+5x-5=0

Applicando la formula risolutiva otteniamo le soluzioni:

x_1=\dfrac{-5+3\sqrt{5}}{2}; \qquad x_2=\dfrac{-5-3\sqrt{5}}{2}

Mentre è evidente che {x_2} è negativa, non è altrettanto immediato stabilire il segno della soluzione {x_1}. Si arriva comunque rapidamente a determinare il segno di {x_1} ragionando sulla quantità {\sqrt{5}}, tuttavia vediamo di utilizzare la regola di Cartesio.

Poiché nell’equazione abbiamo una permanenza e una variazione, dobbiamo avere una soluzione positiva e una negativa. E dato che {x_2} è evidentemente negativa, concludiamo che {x_1} è positiva. Infatti, a riprova di ciò:

x_1=\dfrac{-5+3\sqrt{5}}{2}\approx 0,85 > 0

Un’altra utilità della regola di Cartesio è data dalla possibilità di studiare il segno delle soluzioni di un’equazione parametrica al variare del parametro, come mostra il seguente esempio.

Studio del segno delle soluzioni parametriche di un’equazione di secondo grado letterale

Consideriamo l’equazione:

x^2+2kx+k^2=0

Anzitutto calcoliamo il determinante:

\Delta = b^2-4ac=(2k)^2-4 \cdot 1 \cdot k^2=4k^2-4k^2=0

Dunque per ogni valore reale di {k} avremo per l’equazione due soluzioni reali e coincidenti. Vediamo ora di determinare il segno delle soluzioni.

Il coefficiente {a} è uguale a {1} e di conseguenza non dipende dal parametro. Invece i coefficienti {b=2k} e {c=k^2} dipendono dal parametro. Tuttavia, il coefficiente {c} è un quadrato ed è quindi positivo per ogni {k}. Allora, l’unico coefficiente il cui segno dipende dal parametro è {b}.

Il coefficiente {b} è positivo se:

2k > 0 \iff k > 0

Quindi per {k> 0 } nell’equazione abbiamo una permanenza (coefficienti {a} e {b} positivi) e un’altra permanenza (infatti {c=k^2} è come detto positivo).

Di conseguenza, per {k> 0 } avremo due soluzioni negative.

Vediamo infine cosa succede per {k< 0}. In questo caso nell’equazione abbiamo due variazioni. Infatti, il coefficiente {a} è positivo e il coefficiente {b} è negativo (una variazione). Inoltre, il coefficiente successivo a {b} è positivo (altra variazione). Di conseguenza, per {k<0} abbiamo due soluzioni entrambe positive.

Troviamo conferma dei risultati risolvendo l’equazione parametrica, la quale fornisce le soluzioni parametriche:

x_1=x_2 = -k, \qquad k \in \mathbb{R}

soluzioni evidentemente entrambe negative per {k>0} ed entrambe positive per {k<0}.

L’esempio visto sulle equazioni parametriche è piuttosto semplice. Le cose si complicando invece nel caso ad esempio di coefficienti aventi tutti segno dipendente dal parametro. In tal caso occorrerà studiare i segni dei coefficienti in funzione del parametro aiutandosi per via grafica. In tal modo sarà possibile individuare i vari casi possibili di variazioni e permanenze proprio in funzione del valore del parametro. E con ciò si potranno stabilire i segni delle soluzioni parametriche.

Esempio (studio del segno delle soluzioni parametriche in un caso più generale)

Studiare il segno delle soluzioni dell’equazione parametrica:

2kx^2+(1-2k^2)x-k=0

Vediamo anzitutto quando il determinante è maggiore o uguale a zero (chiaramente per {\Delta<0} studiare il segno delle soluzioni non ha senso):

\begin{align*} & \Delta = (1-2k^2)^2-4 \cdot 2k \cdot (-k) =  \\ \\ & =1+4k^4-4k^2+8k^2=1+4k^4+4k^2=(1+2k^2)^2 \end{align*}

Il discriminante è comunque in questo caso positivo per ogni valore di {k}. Ha dunque senso determinare il segno delle soluzioni dell’equazione per ogni valore reale del parametro, ad eccezione di {k=0}. Infatti, per quest’ultimo valore l’equazione diventa di primo grado.

Studiamo a questo punto i segni dei coefficienti {a, \: b} e {c}. Prima di tutto, occupiamoci separatamente dello studio del segno del coefficiente {b=1-2k^2}. Trattandosi di un polinomio di secondo grado in {k}, scomponiamolo in fattori e quindi studiamo il segno dei fattori:

1-2k^2=(1-\sqrt{2}k)(1+\sqrt{2}k)

Abbiamo:

Quindi il coefficiente {b} è positivo per {-\dfrac{1}{\sqrt{2}}<k<\dfrac{1}{\sqrt{2}}}.

Veniamo ora ai rimanenti coefficienti dell’equazione. Il coefficiente {a=2k} è evidentemente positivo per {k >0}, mentre infine il coefficiente {c=-k} è positivo per {k<0}.

Riepiloghiamo tutti i risultati dello studio dei segni dei coefficienti dell’equazione nel seguente diagramma:

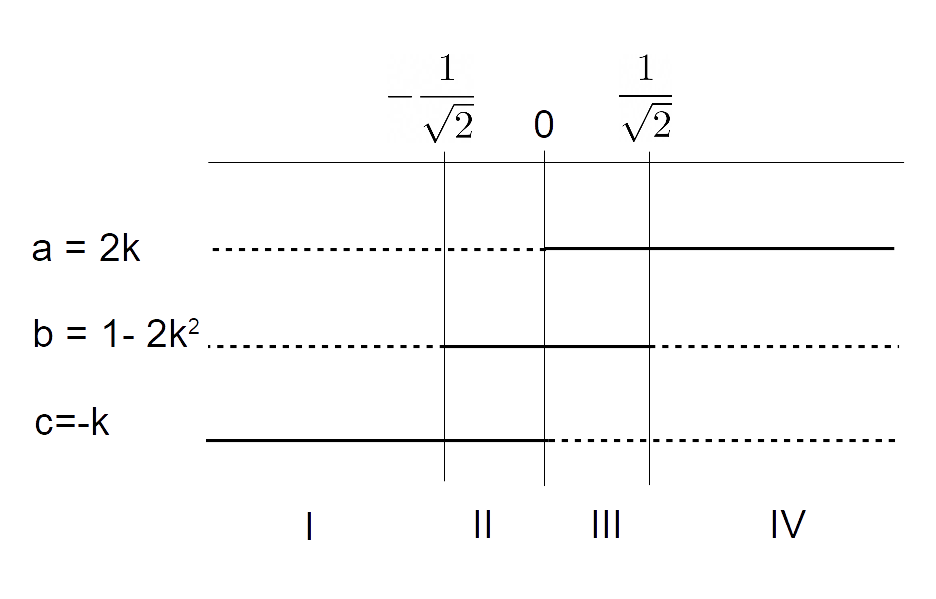
Attenzione: dobbiamo leggere il diagramma in senso verticale considerando il segno che assume ogni coefficiente in ciascun intervallo (gli intervalli sono indicati con i numeri romani).

Nel primo intervallo abbiamo una permanenza e una variazione, di conseguenza per {k<-\dfrac{1}{2}} le due soluzioni sono discordi.

Nel secondo intervallo abbiamo una variazione e una permanenza, e quindi anche per {-\dfrac{1}{\sqrt{2}}<k<0} avremo due soluzioni discordi.

Procedendo in questo modo è immediato rilevare che anche negli altri due intervalli abbiamo rispettivamente una permanenza e una variazione e una variazione e una permanenza, per cui in conclusione le soluzioni dell’equazione data risultano discordi per ogni valore reale del parametro (escluso {k = 0 } e {k=\pm \dfrac{1}{\sqrt{2}}}, valori che annullano dei coefficienti dell’equazione e per i quali a rigore dovremmo fare dei ragionamenti a parte).

Possiamo verificare immediatamente i risultati ottenuti sullo studio dei segni delle soluzioni. Infatti, tenendo conto che le soluzioni parametriche dell’equazione sono:

x_1 = -\dfrac{1}{2k}, \qquad x_2 = k

se i risultati sui segni delle soluzioni sono corretti (soluzioni discordi), il prodotto delle soluzioni dovrà essere sempre negativo. Ed effettivamente la disequazione:

x_1 \cdot x_2 < 0 \iff \left( -\dfrac{1}{2k}\right)\cdot k  < 0

risulta verificata per ogni {k \neq 0}.

Per quanto riguarda la regola di Cartesio applicata alle equazioni di secondo grado è tutto. Nella prossima lezione ci occuperemo dei problemi di secondo grado (problemi risolvibili con le equazioni di secondo grado). Un saluto a tutti voi!