Scomporre un polinomio con Ruffini

 - 

Monomi e polinomi (superiori)

In questa lezione vediamo come scomporre un polinomio con la regola di Ruffini. Il metodo si basa sul teorema di Ruffini e sul teorema del resto, grazie ai quali è eventualmente possibile individuare un divisore del tipo {x-c} per il polinomio da scomporre.

Così, individuato se possibile un tale divisore, per scomporre un dato polinomio {P(x)}con la regola di Ruffini basterà scrivere:

P(x)=Q(x) \cdot (x-c)

ove {Q(x)} è il quoziente esatto della divisione {P(x):(x-c)}.

Osserviamo che {c} è un valore che annulla {P(x)}. Ciò si giustifica ricordando che, per il teorema del resto, il resto della divisione {P(x):(x-c)} è uguale alla valutazione {P(c)}, ovvero al valore che il polinomio assume per {x=c}. Inoltre, se tale valore è zero, per il teorema di Ruffini {x-c} è un divisore di {P(x)}, per cui la divisione {P(x):(x-c)} è esatta. E di conseguenza vale la relazione precedente che esprime il polinomio come prodotto del quoziente per il divisore.

Per tutto quanto detto, il primo passo per scomporre un polinomio con la regola di Ruffini è dato dal ricercare una radice del polinomio, ovvero un valore {c} che annulla il polinomio, cioè tale che {P(c)=0}.

Nella lezione ci occuperemo di tutti i casi:

• come scomporre un polinomio con la regola di Ruffini utilizzando radici intere o frazionarie;
• come scomporre un polinomio con la regola di Ruffini nel caso di polinomio con più lettere.

Fatte le dovute premesse vediamo subito la scomposizione di un polinomio con la regola di Ruffini.

Metodo pratico per scomporre un polinomio con la regola di Ruffini

Supponiamo di dover scomporre il polinomio:

P(x) = x^3+3x^2-10x-24

Il primo passo consiste nel ricercare un valore {c} tale che {P(c)=0}. Dobbiamo cioè trovare una radice {c} del polinomio.

La regola generale afferma che tutti i divisori del termine noto del polinomio, presi con segno positivo e negativo, sono possibili radici per il polinomio stesso. Questi sono tutti i possibili divisori nel caso in cui il coefficiente di grado massimo del polinomio sia {1} (e siamo in questa situazione, poiché il coefficiente di {x^3} è proprio {1}). Qualora tale coefficiente sia diverso da {1}, avremo anche altri possibili divisori (vedremo la regola generale nella sua completezza più avanti nella lezione).

Così i possibili zeri o radici di {P(x)} sono:

\pm1, \: \pm2, \: \pm3, \: \pm4, \: \pm6, \: \pm8,\: \pm12, \: \pm 24

Si tratta a questo punto di testare con pazienza i valori, sostituendo alla {x} ciascuno di essi. Ci fermeremo non appena avremo trovato un valore per cui la valutazione del polinomio risulta uguale a zero. Abbiamo:

P(-2)=(-2)^3+3(-2)^2-10(-2)-24=-8+12+20-24=0

Quindi abbiamo trovato una radice per il polinomio pari a {c=-2}. Di conseguenza, il polinomio {P(x)} sarà divisibile per {x-c}, ovvero per {x-(-2)=x+2}. Quindi il binomio {x+2} è un divisore del polinomio {x^3+3x^2-10x-24}. Ciò significa che il quoziente {Q(x)} della divisione:

(x^3+3x^2-10x-24):(x+2)

sarà esatto e consentirà di scomporre il polinomio come:

x^3+3x^2-10x-24=Q(x)(x+2)

Ora, per trovare il quoziente {Q(x)} è in teoria possibile eseguire la divisione utilizzando la regola generale. Tuttavia, è di fatto obbligatorio poiché estremamente conveniente utilizzare la regola di Ruffini. Infatti dobbiamo dividere il polinomio {P(x)} per un polinomio di primo grado.

Cominciamo allora a compilare la tabella, scrivendo i coefficienti del polinomio ordinato da scomporre e scrivendo il valore della radice {c} nell’apposito spazio sulla sinistra:

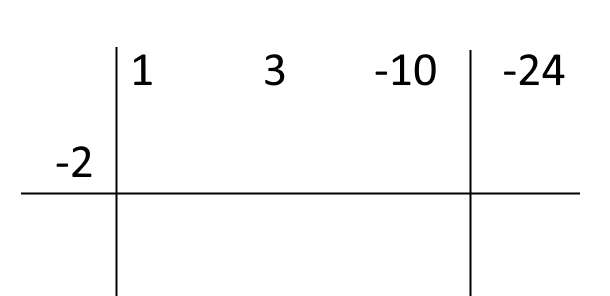
Riportiamo il primo coefficiente del polinomio nella parte in basso:

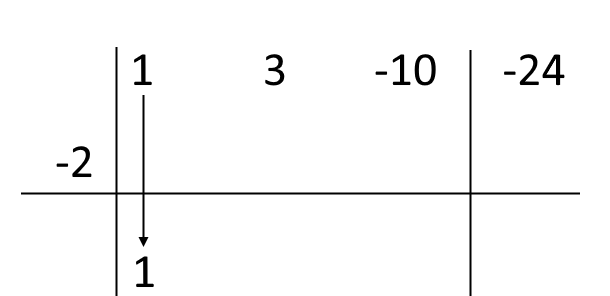
A questo punto moltiplichiamo il valore della radice per l’ultimo numero scritto: {-2 \cdot 1 = -2}. Scriviamo il risultato sotto al secondo coefficiente del polinomio {P(x)}:

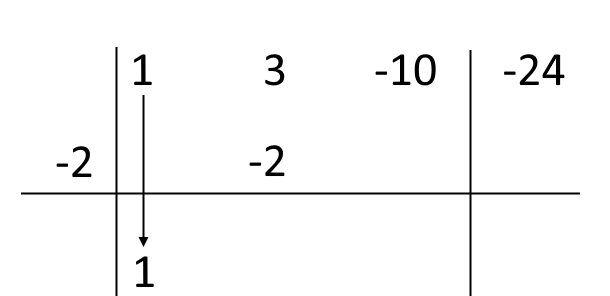
Ora sommiamo algebricamente l’ultimo numero scritto con il numero sopra di esso (quindi {3+(-2)=3-2=1}):

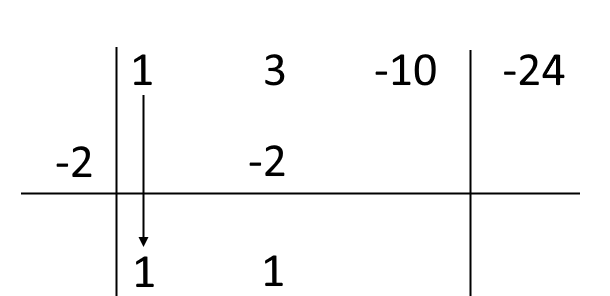
A questo punto moltiplichiamo la radice per l’ultimo numero scritto: {-2 \cdot 1 = -2}. Scriviamo il risultato sotto al terzo coefficiente del polinomio {P(x)}:

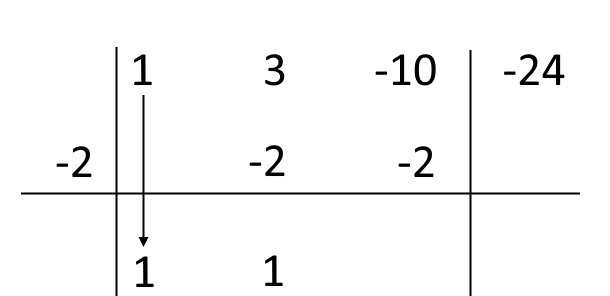
A questo punto sommiamo algebricamente l’ultimo numero scritto con quello sopra di esso (quindi {-10+(-2)=-10-2=-12}):

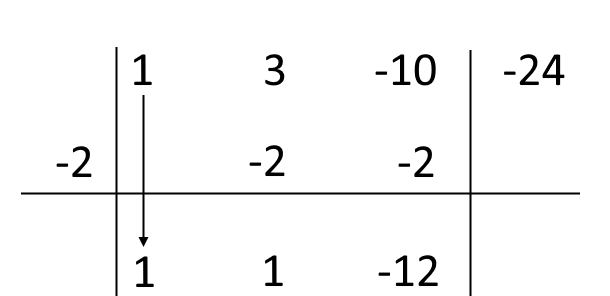
Ora siamo quasi arrivati. Moltiplichiamo la radice {-2} per l’ultimo numero scritto ({-2 \cdot (-12) = 24}), e scriviamo il risultato ottenuto sotto il termine noto di {P(x)}:

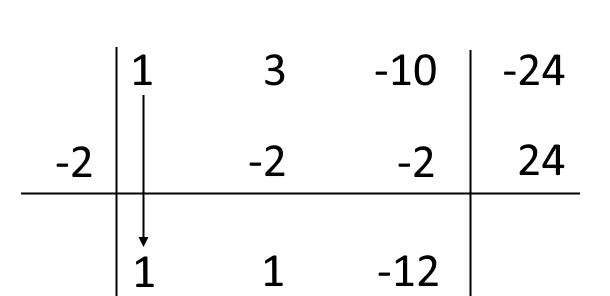
Ed ora siamo al passaggio conclusivo. Sommiamo algebricamente tra loro l’ultimo numero scritto e quello sopra di esso: {-24+24=0}. Scriviamo nell’ultimo spazio rimanente il risultato:

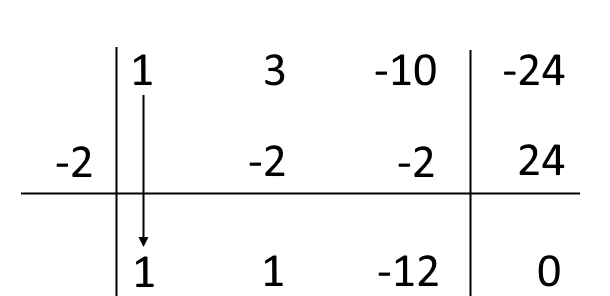
Osserviamo che questo ultimo numero rappresenta il resto della divisione e deve essere zero. Infatti, poiché {c=-2} è una radice di {P(x)}, per i teoremi del resto e di Ruffini il resto della divisione {P(x):(x-c)} non può essere che zero. Se otteniamo un resto diverso da zero, ciò significa che abbiamo fatto qualche errore nei calcoli relativi alla tabella della regola di Ruffini.

Ora, i numeri presenti nell’ultima riga, tolto il resto, sono ordinatamente i coefficienti del quoziente {Q(x)}. E poiché {P(x)} è di terzo grado, e poiché {x-c} è di primo grado, il quoziente sarà necessariamente di secondo grado (differenza tra il grado del dividendo e il grado del divisore, {3-1=2}). Così abbiamo:

Q(x)=x^2+x-12

e in conclusione possiamo scrivere:

P(x)=Q(x)\cdot (x-c) 

ovvero nel nostro caso, ricordando che {c=-2}:

x^3+3x^2-10x-24=(x^2+x-12)(x+2)

E questa è una prima scomposizione del polinomio {x^3+3x^2-10x-24}. Abbiamo così visto come scomporre un polinomio con la regola di Ruffini.

Ora, la scomposizione non è finita poiché {x^2+x-12} può essere ulteriormente scomposto. E’ conveniente utilizzare la regola del trinomio caratteristico, anche se in teoria è ancora possibile utilizzare la regola di Ruffini. Osserviamo che la scomposizione con la regola di Ruffini è conveniente soltanto finché non si arriva nella scomposizione ad un fattore di secondo grado.

Nel nostro caso abbiamo (trinomio caratteristico):

(x^2+x-12)=(x+4)(x-3)

E quindi scrivendo la scomposizione finale del polinomio di partenza:

x^3+3x^2-10x-24=(x^2+x-12)(x+2)=(x+4)(x-3)(x+2)

In generale sarà conveniente se possibile scomporre tramite la regola di Ruffini un polinomio di quarto grado come il prodotto di un polinomio di terzo grado per un polinomio di primo grado. A tal punto se possibile scomporremo di nuovo con la regola di Ruffini il polinomio di terzo grado come prodotto di un polinomio di secondo grado per un polinomio di primo grado.

Così in tal caso scriveremo il polinomio di quarto grado di partenza come prodotto di un polinomio di secondo grado per due polinomi di primo grado. E a tal punto scomporremo se possibile il polinomio di secondo grado con altri metodi, arrivando all’eventuale scomposizione finale data dal prodotto di soli polinomi di primo grado.

La regola di Ruffini può quindi essere utilizzata in modo ricorsivo, come mostra il seguente esempio completo.

Utilizzo in forma ricorsiva della regola di Ruffini (scomposizioni successive)

Scomporre il seguente polinomio:

P(x)=x^4-3x^3-15x^2+19x+30

Come sempre quando è in ballo la divisione tra polinomi assicuriamoci che il polinomio sia ordinato e completo. In questo caso ci siamo. Diversamente occorrerà ordinare il polinomio e considerare coefficiente zero per i termini mancanti (es., il polinomio {x^2+2x^3+7} dovrà essere riscritto come 2x^3+x^2+0x+7, scrivendo poi nella tabella un coefficiente {0} per il termine in {x}).

Ricerchiamo una radice per il polinomio dato tra i divisori positivi e negativi del termine noto. Abbiamo:

\small P(-1)=(-1)^4-3(-1)^3-15(-1)^2+19(-1)+30=+1+3-15-19+30=0

Pertanto {c=-1} è una radice per il polinomio da scomporre e quindi {x-c=x-(-1)} ovvero {x+1} è un divisore per il polinomio stesso. La divisione {P(x):(x+1)} dovrà allora dare un quoziente esatto (e pertanto il resto sarà zero).

Utilizzando la regola di Ruffini:

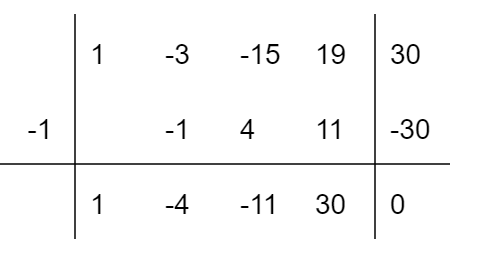
Il quoziente dovrà essere di grado {4-1=3}, e tenendo conto dei coefficienti che abbiamo calcolato si ha {Q(x)=x^3-4x^2-11x+30}. Abbiamo allora intanto la scomposizione:

x^4-3x^3-15x^2+19x+30=(x^3-4x^2-11x+30)(x+1)

E di nuovo possibile scomporre il polinomio di terzo grado con la regola di Ruffini. Infatti abbiamo per il polinomio {x^3-4x^2-11x+30} la radice {c=2}. Il polinomio è quindi divisibile per {x-2} ed applicando in modo del tutto simile ai casi precedenti la regola di Ruffini otteniamo la scomposizione:

x^3-4x^2-11x+30=(x^2-2x-15)(x-2)

Così tenendo conto di entrambe le scomposizioni sin qui scritte:

x^4-3x^3-15x^2+19x+30=(x^2-2x-15)(x-2)(x+1)

Ora è possibile infine scomporre il polinomio {x^2-2x-15} con la regola del trinomio caratteristico, ottenendo {x^2-2x-15=(x-5)(x+3)}. Di conseguenza per il polinomio di partenza abbiamo la scomposizione finale:

x^4-3x^3-15x^2+19x+30=(x-5)(x+3)(x-2)(x+1)

Ricerca delle radici per polinomi con coefficiente del termine di grado massimo diverso da 1

Supponiamo di voler scomporre con la regola di Ruffini il seguente polinomio:

2x^3-3x^2+16x+9

Stavolta il coefficiente del termine di grado massimo è diverso da {1} e per la ricerca delle radici la regola è leggermente diversa.

Le possibili radici sono date dai rapporti tra ciascuno dei divisori del termine noto per ciascuno dei divisori del coefficiente del termine di grado massimo.

I divisori del termine noto {9} sono:

\pm 1, \: \pm 3, \: \pm9

mentre i divisori del coefficiente del termine di grado massimo (ovvero il coefficiente di {2x^£}) sono:

\pm 1, \: \pm 2

Così le possibili radici sono date dai rapporti (ne riportiamo solo una parte):

\pm1, \: \dfrac{\pm3}{\pm 1}, \: \dfrac{\pm9 }{\pm1}, \: \dfrac{\pm 1}{\pm 2}, \:\dfrac{\pm3}{\pm2}\dots

considerando per il numeratore e il denominatore di ciascun rapporto tutti i possibili segni, e quindi la conseguente frazione.

In questo caso uno zero del polinomio è dato dalla frazione {-\dfrac{1}{2}}:

\begin{align*}  P\left( -\dfrac{1}{2}\right) &=2 \cdot \left( -\dfrac{1}{2}\right)^3-3\left( -\dfrac{1}{2}\right)^2+16 \cdot \left(-\dfrac{1}{2} \right)+9=\\ \\ & = 2 \cdot \left( -\dfrac{1}{8}\right)-3 \cdot \dfrac{1}{4} -8+9=-1-8+9=0\end{align*}

A questo punto procediamo scomponendo il polinomio con la regola di Ruffini, con {c=-\dfrac{1}{2}}, tenendo conto che di conseguenza un divisore del polinomio è {x+\dfrac{1}{2}}:

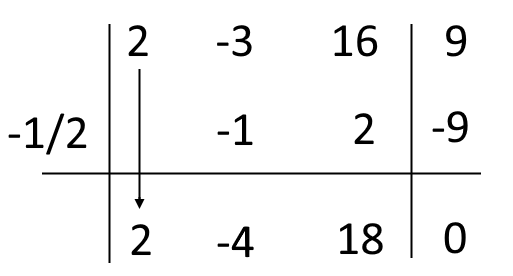
\begin{align*} & 2x^3-3x^2+16x+9=(2x^2-4x+18)\left(x+\dfrac{1}{2}\right) = \\ \\ & =(2x^2-4x+18)\left( \dfrac{2x+1}{2}\right) =\dfrac{1}{2}(2x^2-4x+18)(2x+1)=\\ \\ & =(x^2-2x+9)(2x+1)\end{align*}

La scomposizione si conclude qui poiché non è possibile scomporre il polinomio {x^2-2x+9}. Esso non è infatti un trinomio caratteristico poiché non è possibile individuare due numeri aventi somma {-2} e prodotto {9}.

Osservazione. Un polinomio del tipo {ax^2+bx+c} non è sicuramente scomponibile in fattori se la quantità {\Delta=b^2-4ac} risulta minore di zero. Nel caso del polinomio {x^2-2x+9} abbiamo {a=1, \: b=-2, \: c=9} e infatti risulta: {(-2)^2-4 \cdot 1 \cdot 9 = 4-36<0}

Scomporre con la regola di Ruffini di un polinomio con più lettere

Vediamo come scomporre con la regola di Ruffini un polinomio con più lettere. Proviamo a scomporre il polinomio:

x^3-5ax^2+7a^2x-3a^3

In modo del tutto simile al caso del trinomio caratteristico con più lettere, l’idea è quella di scegliere una lettera come variabile e considerare l’altra lettera come parametro. Consideriamo ad esempio la lettera {x} come variabile e la lettera {a} come parametro.

Con queste ipotesi, siamo in presenza di un polinomio nella variabile {x} con coefficiente {1} per il termine di terzo grado (il grado è riferito alla variabile {x}), coefficiente {-5a} per il termine di secondo grado, coefficiente {7a^2} per il termine di primo grado e termine noto {-3a^3}.

Cominciamo ricercando una radice per il polinomio, ovvero in questo caso un monomio che sostituito alla {x} annulla il polinomio.

Osserviamo che sostituendo alla variabile {x} la quantità {a} abbiamo:

\small P(a)=a^3-5a \cdot a^2+ 7 a^2 \cdot a-3a^3=a^3-5a^3+7a^3-3a^3=0

Di conseguenza {c=a} è una radice per il polinomio da scomporre e di conseguenza {x-a} è un suo divisore. Calcoliamo a questo punto il quoziente con la regola di Ruffini:

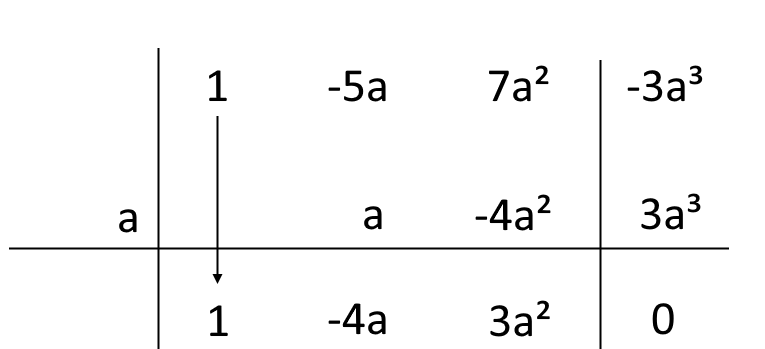
Poiché il polinomio di partenza è di terzo grado rispetto alla variabile {x}, il quoziente sarà di secondo grado sempre rispetto alla variabile {x}. I coefficienti ottenuti nell’ultima riga della tabella sono i coefficienti parametrici del quoziente ed abbiamo:

Q(x)=x^2-4ax+3a^2

Così possiamo scrivere la scomposizione:

x^3-5ax^2+7a^2x-3a^3=(x^2-4ax+3a^2)(x-a)

Ora, il polinomio {x^2-4ax+3a^2} può essere scomposto utilizzando la regola del trinomio caratteristico nel caso di più lettere (vedi precedente lezione). Dobbiamo ricercare due quantità la cui somma sia {-4a} e il cui prodotto sia {3a^2}. Osserviamo che la somma {-4a} è negativa mentre il prodotto {3a^2} è positivo. Per cui le due quantità avranno entrambe segno meno. Inoltre, esse dovranno essere di primo grado rispetto ad {a} (di modo che il loro prodotto sia di secondo grado). Le due quantità sono {-3a} e {-a}. Infatti {-3a + (-a) = -4a} ed inoltre {-3a \cdot (-a) = 3a^2}. Così abbiamo:

x^2-4ax+3a^2=(x-3a)(x-a)

E quindi in conclusione per il polinomio di partenza vale la scomposizione:

\begin{align*} &x^3-5ax^2+7a^2x-3a^3=(x^2-4ax+3a^2)(x-a) = \\ \\ & =(x-3a)(x-a)(x-a)=(x-3a)(x-a)^2\end{align*}

Conclusioni

Per quanto riguarda le tecniche su come scomporre un polinomio con la regola di Ruffini è tutto. Ribadiamo ancora che il metodo si basa sulle conseguenze del teorema del resto e del teorema di Ruffini, i quali consentono di individuare un divisore del tipo {x-c} del polinomio di partenza, che utilizzeremo per la scomposizione dello stesso polinomio.

Buon proseguimento!