Cominciamo ora ad occuparci del problema della scomposizione dei polinomi in fattori fornendo in questa lezione una introduzione generale. Nelle lezioni successive ci occuperemo più nel dettaglio di ogni singolo metodo di scomposizione, fornendo ulteriori esempi.
Per scomposizione dei polinomi in fattori intendiamo un procedimento che consente, se possibile, di riscrivere un polinomio {P} di grado {n} nel prodotto di almeno due polinomi {P_1} e {P_2}, aventi grado rispettivamente {n_1} ed {n_2}, con {n_1 < n} ed {n_2 < n}. Per quanto sappiamo sul grado del prodotto tra polinomi avremo ovviamente {n=n_1+n_2}.
Se dunque è possibile riscrivere il polinomio {P} come:
P=P_1 \cdot P_2
allora diciamo che il polinomio {P} è riducibile o scomponibile in fattori. Precisiamo ancora che i fattori della scomposizione possono anche essere più di due.
In generale non è immediato capire se un certo polinomio può essere scomposto in fattori oppure no. Un aiuto ci viene comunque dato dalla proprietà simmetrica dell’uguaglianza, per la quale se {A=B} allora necessariamente {B=A}. Ed il trucco è quello di applicare la proprietà simmetrica dell’uguaglianza a quanto sappiamo sulla divisione di un polinomio per un monomio e sui prodotti notevoli.
Ad esempio, consideriamo la seguente divisione di un polinomio per un monomio:
(\underbrace{2a^2b+3ab^2-7ab}_{P(a,b)}):(\underbrace{ab}_{D(a,b)})=\underbrace{2a+3b-7}_{Q(a,b)}Per le proprietà della divisione tra polinomi abbiamo di conseguenza:
(\underbrace {2a+3b-7}_{Q(a,b)}) \cdot \underbrace{ab}_{D(a,b)} = \underbrace{2a^2b+3ab^2-7ab}_{P(a,b)}infatti in una divisione tra polinomi tra loro divisibili, il prodotto del quoziente {Q} per il divisore {D} deve restituire il polinomio dividendo {P}.
Ora, applicando la proprietà simmetrica dell’uguaglianza all’ultima relazione possiamo scrivere:
2a^2b+3ab^2-7ab=\left( 2a+3b-7\right) \cdot ab
o il che è lo stesso:
2a^2b+3ab^2-7ab=ab \cdot \left( 2a+3b-7\right)
In altre parole, è possibile scomporre il polinomio {2a^2b+3ab^2-7ab} nel prodotto dei due fattori {ab} e {2a+3b-7}. Così abbiamo riscritto il polinomio di partenza come prodotto del massimo comune divisore dei monomi che lo compongono per il quoziente tra il polinomio stesso e tale MCD.
La procedura appena vista è un metodo di scomposizione e si chiama raccoglimento a fattore comune. In particolare nel caso in esame abbiamo effettuato un raccoglimento con il fattore comune {ab}. La definizione “fattore comune” è dovuta al fatto che effettivamente ciascun termine del polinomio di partenza può essere riscritto come prodotto del fattore comune {ab} per ciascun termine del polinomio {2a+3b-7}. Ad esempio, {2a^2b=ab\cdot 2a} e così via per gli altri termini.
Vedremo tra un istante la regola pratica corrispondente, nei due casi di raccoglimento a fattore comune totale e parziale.
Un’altra importantissima tecnica per scomporre i polinomi consiste nell’applicare la proprietà simmetrica dell’uguaglianza alle regole che abbiamo stabilito per i prodotti notevoli.
Ad esempio grazie al prodotto notevole della somma per differenza possiamo scrivere:
(a+b)(a-b)=a^2-b^2
E per la proprietà simmetrica dell’uguaglianza ciò equivale a scrivere
a^2-b^2=(a+b)(a-b)
In altre parole, è possibile scomporre un polinomio dato dalla differenza dei quadrati di due termini come il prodotto della somma per la differenza dei due termini stessi.
In più, con un ragionamento del tutto simile è possibile stabilire delle regole per la scomposizione dei polinomi a partire da tutte le regole dei prodotti notevoli che abbiamo studiato nelle precedenti lezioni.
Infine, ci occuperemo di ulteriori due metodi di scomposizione che si basano sulla regola di Ruffini per la divisione tra polinomi e su una regola pratica che consente di scomporre particolari trinomi di secondo grado (indicati con il nome di trinomio caratteristico, trinomio particolare o trinomio somma prodotto).
Precisiamo che la scomposizione in fattori dei polinomi è utile ad esempio per:
- semplificare delle particolari frazioni che contengono lettere anche ai denominatori (frazioni algebriche);
- sommare tra loro delle frazioni algebriche mettendole a denominatore comune;
- risolvere alcuni tipi di equazioni.
E questi sono solo alcuni dei casi nei quali la scomposizione in fattori dei polinomi si rivela utile. Con ciò desideriamo quindi invitarvi a studiare con attenzione l’argomento.
Fatte le dovute premesse, vediamo subito le varie regole per scomporre i polinomi in fattori.
Tecniche per la scomposizione dei polinomi
Raccoglimento a fattore comune totale
Per quanto visto nell’introduzione, se esiste un termine che è il massimo comune divisore di tutti i termini di un polinomio, è possibile scomporre tale polinomio nel prodotto del massimo comune divisore stesso per un particolare polinomio quoziente. E il polinomio quoziente è dato dalla divisione del polinomio di partenza per il massimo comune divisore dei suoi termini.
Proviamo ad applicare il principio appena illustrato, per poi ricavarne una regola di pratico uso. Consideriamo il polinomio:
2x^3+7x^2-9x
Osserviamo che il massimo comune divisore tra i monomi {2x^3}, {7x^2} e {-9x} è {x}. Così il quoziente tra il polinomio e l’MCD dei termini che lo compongono è:
(2x^3+7x^2-9x):x=2x^2+7x-9
Di conseguenza, scomponendo il polinomio nel prodotto del MCD dei suoi termini per il quoziente appena calcolato abbiamo:
2x^3+7x^2-9x=x(2x^2+7x-9)
Nella pratica diciamo che abbiamo messo in evidenza il termine {x} nel polinomio. E in modo del tutto equivalente, quello che dobbiamo fare è:
- dividere ciascun termine del polinomio di partenza per il MCD di tutti i suoi termini;
- allo stesso tempo moltiplicare il risultato ottenuto per il MCD stesso.
Così più brevemente avremo:
2x^3+7x^2-9x=x\left( \dfrac{2x^3}{x}+\dfrac{7x^2}{x}-\dfrac{9x}{x}\right)=x(2x^2+7x-9)Nella pratica dividiamo mentalmente ciascun termine del polinomio di partenza per il MCD dei suoi termini e scriviamo direttamente:
2x^3+7x^2-9x=x(2x^2+7x-9)
Forniamo ora la regola generale da utilizzare.
Sia dato un polinomio {P}. Se esiste un massimo comune divisore diverso da {1} di tutti i suoi termini, possiamo scomporre il polinomio nel prodotto del MCD stesso per un polinomio che si ottiene da quello di partenza dividendo ciascuno dei suoi termini per il MCD.
In tal modo diciamo che abbiamo effettuato un raccoglimento a fattore comune, mettendo in evidenza il MCD dei termini del polinomio.
Ricordando la definizione di massimo comune divisore tra monomi, ciò consiste nel mettere in evidenza un monomio che abbia parte numerica data dal MCD delle parti numeriche dei termini del polinomio da scomporre, e parte letterale costituita dalle lettere comuni a tutti i termini del polinomio, accompagnate dal più piccolo tra gli esponenti presenti nel polinomio per ciascuna lettera.
Vediamo subito un esempio relativo ad un polinomio con più lettere. Scomponiamo in fattori il polinomio:
8a^2b^4+4a^2b^2+16a^4b^2
Il MCD tra i coefficienti dei termini del polinomio è {4}. Le lettere in comune ai termini sono {a} e {b}. Per la lettera {a} l’esponente più piccolo che compare nei termini del polinomio è {2}, e per la lettera {b} l’esponente più piccolo è {2}. Di conseguenza è possibile raccogliere per il termine {4a^2b^2}:
\left( 8a^2b^4+4a^2b^2+16a^4b^2\right)=4a^2b^2(2b^2+1+4a^2)
Osserviamo che il fattore {2b^2+1+4a^2} è ottenuto dividendo ciascun termine del polinomio di partenza per il termine messo in evidenza, ovvero {4a^2b^2}. Scrivendo per maggior chiarezza tutti i passaggi:
\begin{align*} & \left( 8a^2b^4+4a^2b^2+16a^4b^2\right)=\\ \\ & = 4a^2b^2\left( \dfrac{8a^2b^4}{4a^2b^2}+\dfrac{4a^2b^2}{4a^2b^2}+\dfrac{16a^4b^2}{4a^2b^2}\right)=\\ \\ & =4a^2b^2(2b^2+1+4a^2) \end{align*}In caso di dubbi consigliamo un ripasso sulla divisione tra monomi.
Raccoglimento a fattore comune parziale
Può capitare che non sia possibile raccogliere nessun termine in un polinomio. Questo avviene quando non esiste alcun monomio diverso da {1} che sia il MCD di tutti i termini del polinomio.
Tuttavia, può essere possibile riscrivere il polinomio da scomporre come somma di due polinomi, tali che per ciascuno di essi sia possibile determinare il MCD di tutti i suoi termini. In tal caso, potremo eseguire il raccoglimento a fattore comune limitatamente a ciascuno dei due polinomi, eseguendo un raccoglimento a fattore comune parziale.
A tal punto, dovremo poi ritrovarci nella condizione di poter eseguire un raccoglimento a fattore comune totale, in modo da poter scomporre in fattori il polinomio di partenza. Se ciò non accade, vuol dire che il polinomio non può essere scomposto utilizzando questo metodo.
Consideriamo ad esempio il polinomio:
4ax-4bx+ay-by
E’ evidente che non esiste un MCD diverso da {1} di tutti i termini del polinomio. Tuttavia, possiamo riscrivere il polinomio come somma di due polinomi:
(4ax-4bx)+(ay-by)
Ed in particolare riusciamo ad individuare un MCD per tutti i termini di ciascun polinomio. Così, per il primo polinomio possiamo effettuare il raccoglimento:
4ax-4bx=4x(a-b)
mentre per il secondo polinomio:
ay-by=y(a-b)
Così sommando tra loro le due scomposizioni in fattori appena scritte abbiamo per il polinomio di partenza:
4ax-4bx+ay-by=4x(a-b)+y(a-b)
Ancora non abbiamo una scomposizione in fattori per il polinomio di partenza, bensì ci ritroviamo con una somma di prodotti. Tuttavia, osserviamo che i due prodotti hanno un fattore in comune: {a-b}. E’ allora possibile raccogliere l’espressione appena scritta proprio per tale fattore comune:
4x(a-b)+y(a-b)=(a-b)(4x+y)
ovvero svolgendo tutti i passaggi per maggior chiarezza:
\begin{align*} & 4x(a-b)+y(a-b)= \\ \\ & =(a-b)\cdot\big[ 4x\underbrace{(a-b):(a-b)}_{1}+y\underbrace{(a-b):(a-b)}_{1}\big]= \\ \\ & =(a-b)(4x+y) \end{align*}Siamo quindi riusciti a scomporre in fattori il polinomio di partenza eseguendo prima due raccoglimenti a fattore comune parziali, poi un raccoglimento a fattore comune totale.
Vediamo un ulteriore esempio. Scomponiamo il polinomio:
-3abx-6acx-3aby-6acy
Osserviamo che il massimo comune divisore tra tutti i coefficienti dei termini è {-3}. Inoltre, abbiamo una sola lettera comune a tutti i termini, la {a}. E questa si presenta in tutti i termini con esponente {1}. Così, possiamo intanto eseguire un raccoglimento a fattore comune totale con il termine {-3a}:
-3abx-6acx-3aby-6acy=-3a\left(bx+2cx+by+2cy\right)=
Ora, osserviamo che il polinomio dentro le parentesi tonde può essere inteso come somma di due polinomi:
=-3a\left[ \left( bx+2cx\right)+\left( by+2cy\right)\right]=
E’ a questo punto possibile raccogliere il primo polinomio per {x} e il secondo polinomio per {y}. In tal modo eseguiamo due raccoglimenti parziali:
=-3a\left[ x(b+2c)+y\left(b+2c\right) \right]=
A questo punto possiamo raccogliere all’interno delle parentesi quadre per il fattore comune {b+2c}:
=-3a[(b+2c)(x+y)]=
e quindi:
=-3a(b+2c)(x+y)
Abbiamo così ottenuto una scomposizione in fattori per il polinomio di partenza e possiamo in conclusione scrivere:
-3abx-6acx-3aby-6acy=-3a(b+2c)(x+y)
Scomposizione dei polinomi con il prodotto somma per differenza
Sia dato il polinomio:
x^2y^2-z^2
In esso riconosciamo la differenza tra il quadrato del termine {xy} e il quadrato del termine {z}. In generale per il prodotto notevole della somma per differenza si ha:
(a+b)(a-b)=a^2-b^2
Per cui la differenza tra i quadrati di due termini sarà uguale al prodotto della loro somma per la loro differenza:
a^2-b^2=(a+b)(a-b)
Per cui nel nostro caso abbiamo:
x^2y^2-z^2=(xy+z)(xy-z)
E’ possibile scomporre una differenza tra i quadrati di due termini come prodotto della somma dei due termini per la loro differenza. E in quest’ultima differenza, il minuendo sarà il termine il cui quadrato è accompagnato nel polinomio di partenza con il segno più, mentre il sottraendo sarà il termine il cui quadrato nel polinomio di partenza è accompagnato dal segno meno.
Ad esempio, scomponiamo il polinomio:
-4a^6b^4+9a^4b^4
Riconosciamo nel termine {4a^6b^4} (il primo termine nel polinomio privato del segno meno) il quadrato di {2a^3b^2}, mentre riconosciamo nel secondo termine {9a^4b^4} il quadrato di {3a^2b^2}. Ora, attenzione, il quadrato che è accompagnato dal segno meno nel polinomio da scomporre è il quadrato del termine {2a^3b^2}. Così questo dovrà comparire nella differenza tra termini che scriveremo nella scomposizione come sottraendo. Abbiamo quindi:
-4a^6b^4+9a^4b^4=(3a^2b^2+2a^3b^2)(3a^2b^2-2a^3b^2)=
Per maggiore praticità avremmo anche potuto riscrivere il polinomio di partenza come {9a^4b^4-4a^6b^4}. In un modo o nell’altro l’importante è prestare attenzione ai segni, seguendo la regola che abbiamo indicato.
Osserviamo che la scomposizione non è terminata. Infatti è possibile eseguire dei raccoglimenti all’interno di ciascuna coppia di parentesi tonde:
=[a^2b^2(3+2a)][a^2b^2(3-2a)]=a^4b^4(3+2a)(3-2a)
Ora la scomposizione è completa.
Quadrato di un binomio
Ricordiamo la regola del prodotto notevole del quadrato di un binomio:
(a+b)^2=a^2+2ab+b^2
Per la proprietà simmetrica dell’uguaglianza:
a^2+2ab+b^2=(a+b)^2
Effettivamente abbiamo ottenuto una scomposizione in fattori poiché la potenza {(a+b)^2} è uguale per definizione al prodotto {(a+b)(a+b)}.
E’ possibile scomporre un trinomio come quadrato di un binomio se nel trinomio sono presenti i quadrati di due quantità e se il rimanente termine del trinomio è il doppio prodotto delle due stesse quantità.
Consideriamo ad esempio il trinomio:
36a^2b^2-12ab+1
Riconosciamo nel primo termine il quadrato del monomio {\boxed{6ab}}. Infatti {(6ab)^2=36a^2b^2}. Il terzo termine è evidentemente il quadrato di {\boxed{1}}. Ora, vediamo se il doppio prodotto dei due termini evidenziati è uguale al terzo termine:
2 \cdot 6ab \cdot 1 = 12ab
Il risultato differisce dal terzo termine del trinomio per un segno. Ciò significa che uno dei due termini fra {6ab} e {1} dovrà essere preso con il segno opposto. Scegliamo allora ad esempio {-1}. Così abbiamo:
36a^2b^2-12ab+1=(6ab-1)^2
Effettivamente, se in un quadrato di un binomio il doppio prodotto è negativo, ciò significa che uno dei due termini del binomio deve essere necessariamente negativo e l’altro positivo.
La necessità di indagare sui segni dei termini è dovuta al fatto che il quadrato di un termine positivo o negativo è sempre positivo.
Ora, se il ragionamento sui segni vi causa problemi, è possibile considerare le due formule separate per la scomposizione con il quadrato di un binomio:
\begin{align*} & a^2+2ab+b^2 = (a+b)^2 ;\\ \\ &a^2-2ab+b^2=(a-b)^2\end{align*}L’importante in un modo o nell’altro è ricordare che il segno che separa i termini nel binomio dipende dal segno del doppio prodotto.
Scomposizione dei polinomi con il quadrato di un trinomio
Ricordiamo la regola del prodotto notevole del quadrato di un trinomio:
(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ac
Per la proprietà simmetrica dell’uguaglianza possiamo anche scrivere:
a^2+b^2+c^2+2ab+2bc+2ac=(a+b+c)^2
e ciò rappresenta la scomposizione in fattori del polinomio di sei termini di partenza.
Se in un polinomio di sei termini riconosciamo i quadrati di tre quantità e i doppi prodotti rispettivamente della prima quantità per la seconda, della seconda quantità per la terza e infine della prima quantità per la terza, allora il polinomio dato è uguale al quadrato della somma delle tre quantità stesse (quadrato di un trinomio).
Consideriamo ad esempio il caso del trinomio:
a^2+b^2+4c^2+2ab+4ac+4bc
Individuiamo nei primi tre termini i quadrati delle quantità rispettivamente {a}, {b} e {2c}. Calcoliamo a questo punto i doppi prodotti tra le possibili coppie delle quantità individuate e vediamo se coincidono con i rimanenti termini del polinomio da scomporre. Abbiamo:
- doppio prodotto della prima quantità per la seconda: {2 \cdot a \cdot b= 2ab};
- doppio prodotto della seconda quantità per la terza: {2 \cdot b \cdot 2c = 4bc};
- infine, doppio prodotto della prima quantità per la terza: {2 \cdot a \cdot 2c = 4ac}.
Effettivamente ciascun doppio prodotto scritto coincide con uno dei rimanenti termini del polinomio di partenza. Così possiamo in conclusione scrivere:
a^2+b^2+4c^2+2ab+4ac+4bc=(a+b+2c)^2
Consideriamo un altro esempio. Scomponiamo in fattori il polinomio:
9x^2+y^2+1-6xy-6x+2y
Ancora, nei primi tre termini riconosciamo dei quadrati. Abbiamo infatti il quadrato, rispettivamente, di {3x}, di {y} e infine di {1}. Veniamo ai doppi prodotti delle quantità che abbiamo individuato:
- doppio prodotto della prima quantità per la seconda: {2 \cdot 3x \cdot y = 6xy};
- doppio prodotto della seconda quantità per la terza: {2 \cdot y \cdot 1 =2y};
- infine, doppio prodotto della prima quantità per la terza: {2 \cdot 3x \cdot 1 = 6x}.
Ora, attenzione. I doppi prodotti corrispondono come valori assoluti ma non sempre come segno. In particolare, l’unico doppio prodotto che ritroviamo con lo stesso segno nel polinomio da scomporre è il secondo, ovvero {2y}. Da ciò deduciamo che entrambi i termini {y} e {1} che fanno parte del doppio prodotto hanno lo stesso segno (ad esempio, prendiamoli entrambi positivi). Di conseguenza, poiché negli altri due doppi prodotti compare il termine {3x} e i corrispondenti termini nel polinomio sono negativi, il termine {3x} stesso dovrà essere negativo. Così, avremo in conclusione per il polinomio di partenza la scomposizione:
9x^2+y^2+1-6xy-6x+2y=(-3x+y+1)^2
Osserviamo che avremmo potuto equivalentemente considerare i termini {3x, \: -y} e {-1} . Infatti, essi soddisfano comunque i requisiti sui segni dei doppi prodotti. Così avremmo potuto altrettanto correttamente scrivere:
9x^2+y^2+1-6xy-6x+2y=\left( 3x-y-1\right)^2
Ciò non è una sorpresa poiché il quadrato di un polinomio e il quadrato del suo opposto coincidono.
Cubo di un binomio
Vediamo ora come scomporre i polinomi utilizzando il cubo di un binomio. Ricordiamo la regola del prodotto notevole del cubo di un binomio:
(a+b)^3=a^3+3a^2b+3ab^2+b^3
Sfruttando la proprietà simmetrica dell’uguaglianza:
a^3+3a^2b+3ab^2+b^3=(a+b)^3
e ciò rappresenta la scomposizione in fattori del polinomio {a^3+3a^2b+3ab^2+b^3}.
Un polinomio ove siano presenti i cubi di due termini e i tripli prodotti rispettivamente del quadrato del primo termine per il secondo termine e del primo termine per il quadrato del secondo termine può essere scomposto come il cubo della somma dei due termini.
Vediamo subito un esempio. Scomponiamo in fattori il polinomio:
27y^3+8+36y+54y^2
Ricerchiamo prima di tutto i termini che sono cubi di certe quantità. Osserviamo che il primo termine è il cubo della quantità {\boxed{3y}}. Infatti {(3y)^3=3^{3}y^3=27y^3}. Inoltre, il secondo termine è il cubo della quantità {\boxed{2}} (infatti {2^3=8}).
Individuate le quantità delle quali compaiono i cubi nel polinomio da scomporre, procediamo scrivendo i due tripli prodotti:
- triplo prodotto del quadrato della prima quantità per la seconda quantità: {3 \cdot (3y)^2 \cdot 2= 3 \cdot 9y^2 \cdot 2 = 54y^2};
- triplo prodotto della prima quantità per il quadrato della seconda quantità: {3 \cdot 3y \cdot 2^2 = 3 \cdot 3y \cdot 4 = 36y}.
Effettivamente i due doppi prodotti scritti sono uguali ai rimanenti termini nel polinomio da scomporre. Riconosciamo allora nel polinomio il cubo di un binomio e possiamo scrivere:
27y^3+8+36y+54y^2=(3y+2)^3
Vediamo un altro esempio. Scomponiamo in fattori il polinomio:
125a^3-75a^2b+15ab^2-b^3
Osserviamo che abbiamo il cubo della quantità {\boxed{5a}} (infatti (5a)^3=125a^3, il primo termine del polinomio). Inoltre, l’ultimo termine del polinomio è il cubo della quantità {\boxed{-b}} (infatti, {(-b)^3=b^3}).
Controlliamo i tripli prodotti:
- triplo prodotto del quadrato della prima quantità per la seconda quantità: {3 \cdot (5a)^2 \cdot (-b) = 3 \cdot 25a^2 \cdot (-b) = -75a^2b};
- triplo prodotto della prima quantità per il quadrato della seconda quantità: {3 \cdot 5a \cdot (-b)^2 = 3 \cdot 5a \cdot b^2 = 15ab^2}.
Effettivamente ritroviamo i due tripli prodotti nei rimanenti termini del polinomio da scomporre, per cui in definitiva possiamo scrivere:
125a^3-75a^2b+15ab^2-b^3=(5a-b)^3
Scomposizione dei polinomi con la somma di cubi e la differenza di cubi
Vediamo un ulteriore metodo per la scomposizione dei polinomi, basato sulla somma di cubi e sulla differenza di cubi. Ricordiamo il prodotto notevole della somma di cubi:
(a+b)(a^2-ab+b^2)=a^3+b^3
Ancora, per la proprietà simmetrica dell’uguaglianza:
a^3+b^3=(a+b)(a^2-ab+b^2)
Allo stesso modo, partendo dalla regola del prodotto notevole della differenza di cubi:
(a-b)(a^2+ab+b^2)=a^3-b^3
sempre grazie alla proprietà simmetrica dell’uguaglianza possiamo scrivere:
a^3-b^3 = (a-b)(a^2+ab+b^2)
Otteniamo allora le due seguenti regole:
La somma dei cubi di due quantità si può scomporre come il prodotto della somma delle due quantità per il falso quadrato della differenza delle due stesse quantità: {a^3+b^3=(a+b)(a^2-ab+b^2)}
La differenza dei cubi di due quantità si può scomporre come il prodotto della differenza delle due quantità per il falso quadrato della somma delle due stesse quantità: {a^3-b^3 = (a-b)(a^2+ab+b^2)}
Consideriamo un primo esempio sulla scomposizione in fattori dei polinomi con le regole appena indicate. Scomponiamo in fattori il seguente polinomio:
y^3-8
Osserviamo che {2^3=8}. Inoltre {(y)^3=y^3}. Per cui ci ritroviamo con la differenza di due cubi. Ed abbiamo rispettivamente il cubo della quantità {y} meno il cubo della quantità {2}. La scomposizione del polinomio dato sarà quindi data dal prodotto della differenza delle due quantità per il falso quadrato della loro somma.
Nello scrivere la differenza, osserviamo che il sottraendo dovrà essere relativo alla quantità il cui cubo nel polinomio da scomporre è accompagnato dal segno meno. Così un fattore della scomposizione sarà dato dalla differenza {y-2}.
Ora, l’altro fattore sarà il falso quadrato della somma delle due quantità, quindi il falso quadrato della somma {y+2}, che è un binomio. Ricordiamo che il falso quadrato di un binomio si costruisce con il quadrato del primo termine, più il prodotto (e non il doppio prodotto) dei due termini, più il quadrato del secondo termine. Così nella scomposizione figurerà il fattore {y^2+2y+4}, ovvero il falso quadrato del binomio {y+2}.
In conclusione abbiamo la scomposizione:
y^3-8= (y-2)(y^2+2y+4)
Consideriamo un ulteriore esempio. Scomponiamo il seguente polinomio:
x^3y^3+1
Riconosciamo immediatamente una somma di cubi (rispettivamente il cubo delle quantità {xy} e {1}). Un fattore sarà quindi dato dalla somma delle due quantità, ovvero il binomio {xy+1}. Per quanto riguarda l’altro fattore, dovremo considerare il falso quadrato del binomio {xy-1}, che è la differenza delle due quantità. Così l’altro fattore sarà dato da {x^2y^2-xy+1}. Di conseguenza possiamo scrivere la scomposizione:
x^3y^3+1=(xy+1)(x^2y^2-xy+1)
Il trinomio caratteristico
Per scomporre dei particolari trinomi di secondo grado che non sono lo sviluppo di un quadrato di un binomio, esiste una regola detta scomposizione con il trinomio caratteristico. Un trinomio di questo tipo si indica anche con il nome di trinomio particolare, o anche trinomio notevole somma e prodotto.
Consideriamo un trinomio caratteristico nella forma:
x^2+sx+p
ove i coefficienti {s} e {p} sono interi e il coefficiente della {x^2} è {1}.
Supponiamo di voler scomporre il trinomio come segue:
(x^2+sx+p)=(x+m)(x+n)
ove {m} e {n} sono interi. Sviluppiamo il secondo membro dell’uguaglianza appena scritta:
\begin{align*} (x^2+sx+p) &=x^2+mx+nx+mn= \\ \\ & = x^2+(m+n)x+mn\end{align*}Affinché tale uguaglianza risulti verificata, per il principio di identità dei polinomi dovrà essere:
\begin{cases} m+n=s \\ \\ mn = p\end{cases}Così in parole povere per scomporre il polinomio dovremo trovare due numeri {m, \: n} la cui somma sia uguale al coefficiente della {x} e il cui prodotto sia uguale al termine noto.
Consideriamo ad esempio il polinomio:
x^2-x-6
Dobbiamo trovare due numeri {m} e {n} tali che la loro somma sia uguale a {-1} (il coefficiente della {x}) e il loro prodotto sia uguale a {-6} (il termine noto).
Per ricercare i due numeri, scriviamo in fila tutti i possibili divisori del termine noto e consideriamo tutte le possibili coppie:
\pm 1, \quad \pm 2, \quad \pm 3, \quad \pm 6
Consideriamo i possibili prodotti tra i valori di ciascuna coppia, prendendo prima i valori più esterni e poi quelli più interni:
\begin{align*} & 1 \cdot 6 = 6; \quad 1 \cdot (-6)=\boxed{-6};\\ \\ & 2 \cdot 3 = 6; \quad -2 \cdot 3 = \boxed{-6}; \quad \underline{\underline{2 \cdot (-3)}} = \boxed{-6} \end{align*}Ora, nelle prove eseguite abbiamo individuato tre coppie di termini il cui prodotto è {-6}. Ora, dobbiamo scegliere solo la coppia la cui somma è pari a {-1}. La coppia di numeri cercati è allora {-3, \: 2}. Infatti {-3 \cdot 2 = -6} e {-3+2 = -1}. Così abbiamo {m=-3} e {n=2} e possiamo in conclusione scrivere:
x^2-x-6=(x-3)(x+2)
ovvero abbiamo riespresso il polinomio da scomporre nella forma {(x+m)(x+n)}.
Caso con coefficiente della {x^2} diverso da 1
Consideriamo il polinomio:
2x^2+5x-3
Non possiamo applicare la precedente regola poiché il coefficiente della {x^2} è diverso da {1}.
L’idea è quella di ricercare due numeri la cui somma sia uguale al coefficiente della {x} e il cui prodotto sia uguale al prodotto del coefficiente della {x^2} per il termine noto. Quindi cerchiamo due numeri {h} e {k} tali che:
h+k = 5; \qquad h\cdot k= 2 \cdot (-3) = -6
Con non troppa difficoltà troviamo i numeri {h=6} e {k=-1}. Ora riscriviamo il coefficiente della {x} del trinomio di partenza come somma dei due numeri trovati:
2x^2+5x-3=2x^2+(6-1)x-3=
A questo punto sviluppiamo l’espressione scritta applicando la proprietà distributiva, senza sommare i valori numerici tra loro:
=2x^2+6x-x-3=
ora non resta che suddividere i termini in due gruppi, e quindi eseguire dei raccoglimenti parziali in modo tale che sia poi possibile eseguire un raccoglimento totale. Ad esempio:
=(2x^2-x)+(6x-3) = x(2x-1)+3(2x-1)=(2x-1)(x+3)
In conclusione possiamo quindi scrivere:
2x^2+5x-3 =(2x-1)(x+3)
Scomposizione con la regola di Ruffini
Vediamo ora la scomposizione dei polinomi utilizzando la regola di Ruffini.
Ricordiamo che grazie alla regola di Ruffini è possibile dividere rapidamente un polinomio {P(x)} per un binomio della forma {x-c}. Inoltre, per il teorema del resto, il resto di tale divisione coincide con la valutazione {P(c)} del polinomio dividendo.
Ma poiché la valutazione {P(c)} è il resto, affinché {P(x)} sia divisibile per {x-c} basta che {c} sia tale da avere {P(c)=0}. Così, {P(x)} è divisibile per {x-c} se {c} è un valore che annulla il polinomio {P(x)}, ovvero una sua radice.
Così, per tale valore di {c} è possibile scrivere:
P(x)=Q(x) \cdot (x-c)
ove {Q(x)} è il quoziente della divisione {P(x):(x-c)}. Così, il polinomio dividendo è uguale al prodotto del quoziente per il divisore (proprietà della divisione tra polinomi). E ciò rappresenta una scomposizione in fattori per il polinomio {P(x)}.
Per determinare {Q(x)} è possibile e conveniente utilizzare la regola di Ruffini.
Consideriamo un esempio pratico. Scomponiamo in fattori il polinomio:
x^3-7x-6
Il primo passo è individuare un valore attribuito alla {x} per il quale si annulla il polinomio. E questo sarà il valore da attribuire alla {c}. In un polinomio di questo tipo, il valore va ricercato tra tutti i divisori del termine noto, ovvero {\pm 1, \: \pm 2, \: \pm3, \: \pm6}. Senza provare tutti questi valori, è abbastanza immediato osservare per come sono i coefficienti del polinomio che questo si annulla per {x=-1}:
P(-1)=(-1)^3-7 (-1)-6 = -1+7-6=0
Così abbiamo {c=-1}. Sostituiamo il valore ottenuto per la {c} nella forma generica del polinomio divisore {x-c}. Otteniamo {x-(-1)=x+1}. Quindi, il polinomio {x+1} è un divisore del polinomio di partenza {x^3-7x-6}. Di conseguenza, il quoziente della divisione {(x^3-7x-6):(x+1)} sarà esatto ed in particolare avremo resto zero.
Ora, calcoliamo il quoziente della divisione utilizzando la regola di Ruffini. Dobbiamo ottenere resto zero.
Ricordiamo di ordinare i polinomi dividendo e divisore e di completare il dividendo se necessario. I polinomi sono ordinati, tuttavia il dividendo non è completo. Dobbiamo allora riscriverlo come {x^3+0x^2-7x-6}. Procediamo costruendo la tabella della regola di Ruffini.
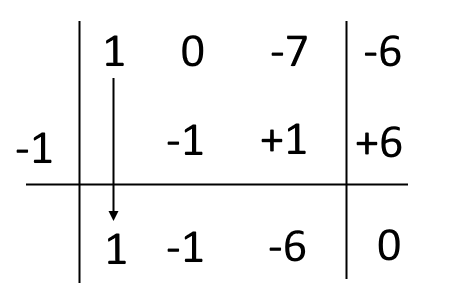
Abbiamo visto come utilizzare la regola nella lezione sulla regola di Ruffini per la divisione tra polinomi.
Abbiamo un quoziente {Q(x)=x^2-x-6} e abbiamo correttamente ottenuto resto {0}. Se il resto è diverso da zero, ciò significa in questo caso che abbiamo fatto un qualche errore. Infatti, come sappiamo {x+1} è un divisore di {x^3-7x-6}.
Così, è possibile esprimere il polinomio di partenza come prodotto del quoziente per il divisore. Vale quindi la scomposizione:
x^3-7x-6=(x^2-x-6)(x+1)
Ora, il polinomio {x^2-x-6} può essere scomposto con la regola del trinomio caratteristico. A rigore è anche possibile utilizzare di nuovo la regola di Ruffini, ma non è conveniente. Con la regola del trinomio caratteristico otteniamo:
x^2-x-6=(x-3)(x+2)
e quindi possiamo in conclusione scrivere:
x^3-7x-6=(x^2-x-6)(x+1)=(x-3)(x+2)(x+1)
e questa è la scomposizione finale.
Conclusioni
Per quanto riguarda questa introduzione alla scomposizione dei polinomi è tutto. Già con le informazioni contenute in questa lezione sarete in grado di scomporre una notevole varietà di polinomi. Nelle prossime lezioni riprenderemo ciascun metodo di scomposizione dei polinomi presentando ulteriori esempi e schede di esercizi correlate. Buon proseguimento!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
