Ci proponiamo ora di studiare insieme il significato geometrico delle disequazioni di primo grado. In particolare, vedremo il problema geometrico corrispondente alla risoluzione di una disequazione di primo grado.
In una disequazione di primo grado in forma normale, il primo membro come vedremo rappresenta l’espressione di una funzione che ha per grafico una retta. Infatti, una funzione che ha per grafico una retta è del tipo:
y=mx+q
ovvero, ribattezzando in modo differente i coefficienti:
y=ax+b
Così ad esempio risolvere la disequazione:
ax+b>0
significa determinare le ascisse dei punti della retta {y=ax+b} che si trovano al di sopra dell’asse delle {x}. In altre parole, individueremo i punti per i quali la funzione {y=ax+b} è positiva. Nei rimanenti punti dell’asse reale la funzione sarà invece negativa, ad eccezione del punto avente ascissa {x=-\dfrac{b}{a}}, che è tale da annullare detta funzione.
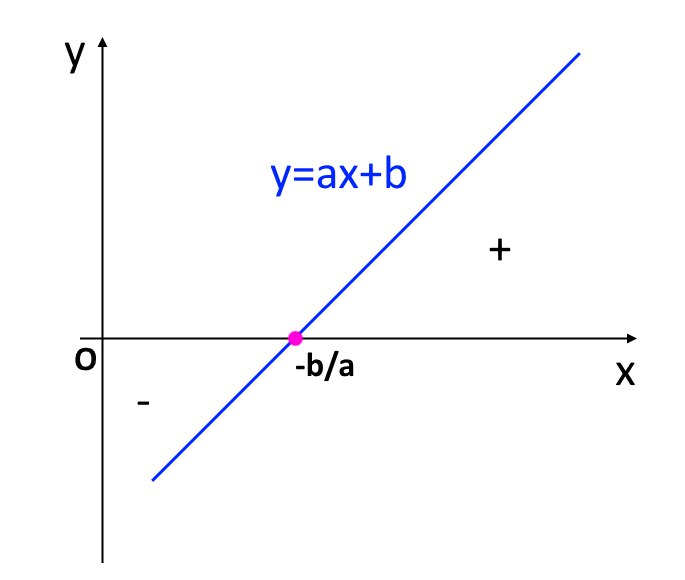
Considerando inoltre disequazioni non in forma normale del tipo ad esempio:
ax+b < cx+d
risolverle significa determinare le ascisse dei punti della retta {y=ax+b} che stanno al di sotto dei punti della retta {y=cx+d}.
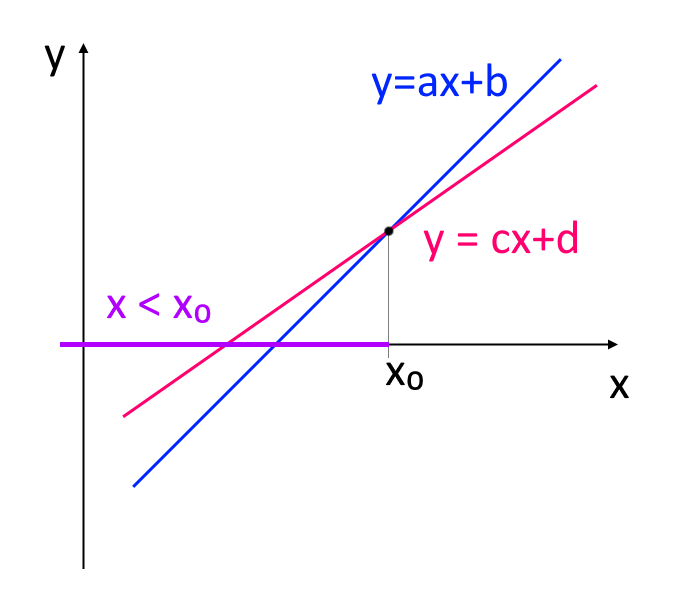
La disequazione è soddisfatta per tutte le {x} minori di {x_0}, le quali effettivamente corrispondono a punti della retta {y=ax+b} che stanno tutti al di sotto della retta {y=cx+d}.
Ma vediamo subito degli esempi relativi al significato geometrico delle disequazioni di primo grado.
Studio del segno della funzione y=ax+b
Grazie alle disequazioni di primo grado è possibile studiare il segno di funzioni del tipo:
y=ax+b
Ad esempio, la funzione sarà positiva in tutti i punti le cui coordinate {x} sono tali da soddisfare la disequazione:
ax+b > 0
Sarà invece negativa in tutti i punti le cui coordinate {x} sono tali da soddisfare la disequazione:
ax+b<0
Infine, la funzione sarà nulla nel punto di ascissa {x} che soddisfa l’equazione:
ax+b=0
Esempi sul significato geometrico delle disequazioni di primo grado
Esempio 1
Studiare il segno della funzione:
y=x+4
La funzione sarà positiva per i valori della {x} tali da soddisfare la disequazione:
x+4 > 0
e quindi, applicando le proprietà delle disequazioni:
x>-4
La funzione sarà invece negativa per i valori della {x} tali da soddisfare la disequazione:
x+4 < 0
e quindi per i valori della {x}:
x < -4
Infine, la funzione sarà nulla per il valore della {x} che verifica l’equazione:
x+4 = 0
ovvero:
x=-4
Possiamo riepilogare graficamente i risultati ottenuti:
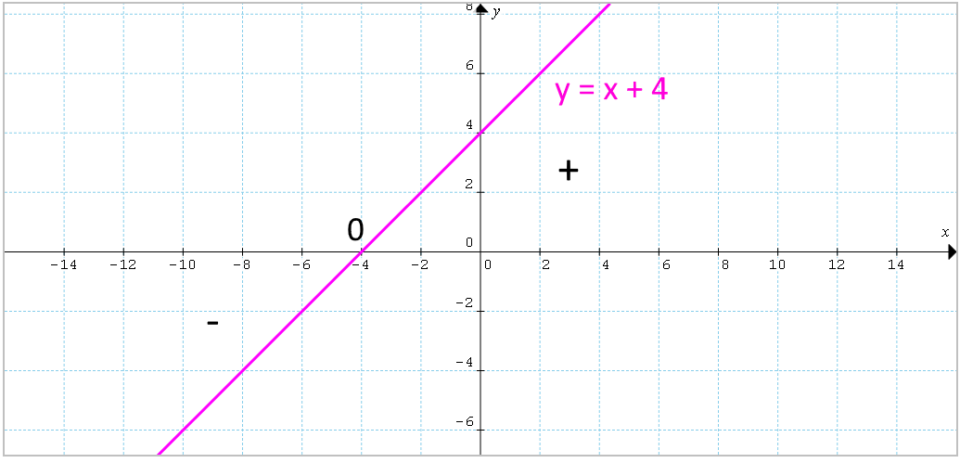
Esempio 2
Determinare per quali valori della {x} il grafico della funzione {y=x+5} si trova al di sopra del grafico della funzione {y=2x-7}.
In questo caso si tratterà di determinare l’insieme delle soluzioni della disequazione:
x + 5 >2x-7
Trasportiamo i termini in modo da avere tutti i termini in {x} nel primo membro e tutti i termini numerici nel secondo membro:
x-2x>-7-5
ovvero:
-x >-12
e quindi in conclusione:
x<12
Vediamo se graficamente troviamo conferma dei risultati ottenuti. Tracciamo le rette corrispondenti alle funzioni {y=x+5} e {y=2x-7} e controlliamo dove si intersecano:
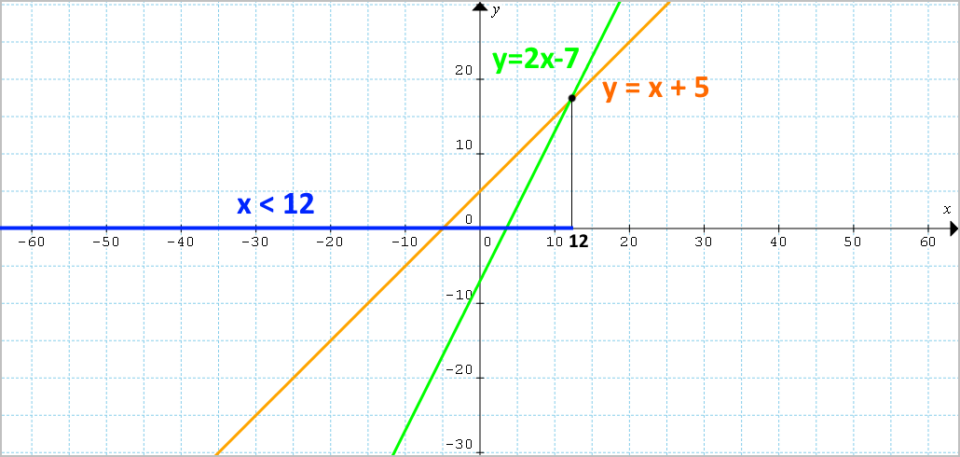
Le rette si intersecano nel punto di ascissa {x=12} e come è immediato osservare la retta {y=x+5} è al di sopra della retta {y=2x-7} per tutti i punti di ascissa {x<12}. Ciò conferma il risultato precedentemente ottenuto per via algebrica.
Per quanto riguarda il significato geometrico delle disequazioni di primo grado è tutto. Come abbiamo visto, esiste un legame tra le disequazioni di primo grado e lo studio del segno di funzioni la cui espressione è data da un polinomio di primo grado. In generale andando avanti nei nostri studi vedremo come effettivamente le disequazioni permettono di effettuare lo studio del segno di funzioni polinomiali, ovvero funzioni del tipo:
y=P(x)
ove {P(x)} è un polinomio di grado {n}. E nella prossima lezione ci occuperemo delle disequazioni prodotto, ovvero di particolari disequazioni del tipo:
P(x) \lesseqgtr 0
ove {P(x)} è un polinomio di grado {n} scomponibile nel prodotto fra polinomi tutti di primo grado {P_1(x) \cdot P_2(x) \cdot 1\dots \cdot P_n(x) }.
In particolare, il nostro obiettivo sarà studiare il segno del polinomio {P(x)} ragionando sui segni dei singoli fattori {P_1(x), \: P_2(x), \dots \: P_n(x)} presenti nella sua scomposizione.
Un saluto a tutti e buon proseguimento con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
