Unione tra insiemi

 - 

Insiemi

L’unione tra insiemi ha come risultato un insieme che contiene tutti gli elementi di entrambi gli insiemi, escluse le eventuali ripetizioni. Così, se intendiamo sommare tra loro due insiemi che hanno degli elementi in comune, nell’insieme che otteniamo come risultato della somma (l’insieme unione) gli elementi in comune dovranno figurare una volta sola.

Vediamo ora come si esegue l’operazione di unione tra insiemi, considerando inizialmente il semplice caso di due soli insiemi. L’unione tra insiemi è la prima delle operazioni tra insiemi che studieremo in questo corso di lezioni.

Nel corso della lezione presenteremo diversi esempi per poter comprendere come si esegue l’unione tra insiemi, anche fra più di due insiemi. Inoltre, mostreremo una semplice rappresentazione grafica dell’operazione mediante i diagrammi di Venn. Infine, a conclusione della lezione enunceremo le principali proprietà dell’operazione di unione tra insiemi.

Definizione di unione tra insiemi

Cominciamo definendo l’operazione insiemistica di unione tra insiemi. Limitiamoci per il momento al semplice caso di due soli insiemi.

Dati due insiemi {A} e {B}, l’operazione di unione tra gli insiemi {A} e {B} restituisce come risultato l’insieme unione {A \cup B} che contiene tutti gli elementi di {A} e tutti gli elementi di {B}.

In senso matematico, possiamo affermare che l’insieme unione, risultato dell’operazione di unione tra due insiemi {A} e {B}, contiene tutti gli elementi che appartengono all’insieme {A} oppure tutti gli elementi che appartengono all’insieme {B}.

Stiamo particolarmente attenti al significato di “oppure”. In senso matematico, intendiamo dire che ciascun elemento dell’insieme unione può appartenere o all’insieme {A}, o all’insieme {B}, senza escludere che possa appartenere anche ad entrambi.

Di conseguenza, possiamo rappresentare l’insieme unione dei due insiemi {A} e {B} come segue:

A \cup B = \{x \in A \: \text{oppure} \: x \in B \}

Osserviamo che al secondo membro dell’uguaglianza appena scritta abbiamo rappresentato l’insieme unione mediante la sua proprietà caratteristica.

Ora, proviamo a fornire una rappresentazione simbolica dell’operazione ancora più rigorosa. In particolare, fissato un sovrainsieme {E} di entrambi gli insiemi {A} e {B}, che prendiamo come insieme universo {E}, possiamo scrivere:

A \cup B = \{x \in E \: | \: x \in A \: \text{oppure} \: x \in B \}

In questo modo abbiamo anche precisato l’insieme universo al quale appartengono gli elementi di entrambi gli insiemi {A} e {B}. Di conseguenza, anche tutti gli elementi dell’insieme unione apparteranno allo stesso insieme universo fissato.

Ricordiamo che {E} è un sovrainsieme per gli insiemi {A} e {B} se valgono entrambe le relazioni di inclusione: {A \subseteq E, \quad B \subseteq E}Tra parentesi, la lettera {E} sta per insieme ambiente, sinonimo di insieme universo (in inglese ambiente si dice environment). Ciò non toglie che l’insieme universo possa anche essere indicato ad esempio con la lettera {U}, che però qui preferiamo non usare poiché somiglia al simbolo dell’operatore di unione tra insiemi, {\cup}.

Per chi è in fase di ripasso e già conosce la logica, è inoltre possibile sostituire la parola “oppure” con il simbolo matematico “{\vee}“, che si riferisce all’operazione di congiunzione logica inclusiva. In questo modo possiamo descrivere l’operazione di unione tra insiemi in modo ancora più formale:

A \cup B = \{x \in E \: | \: x \in A \: \vee \: x \in B \}

A questo punto facciamo subito degli esempi in modo da chiarire la definizione di unione tra insiemi. Come vedrete, non è il caso di farsi spaventare dalle definizioni formali. Si tratta infatti di un’operazione piuttosto intuitiva. 😉

Esempi sull’operazione di unione tra insiemi

Esempio 1

Consideriamo gli insiemi {A=\{1, 3, 5 \}} e {B=\{3, 7, 8 ,10 \}}. L’unione tra i due insiemi è data dall’insieme:

A \cup B = \{1, 3, 5, 7,8,10\}

Osserviamo che non abbiamo ripetuto due volte l’elemento {3}. Infatti, come già sappiamo negli insiemi non possiamo ripetere elementi tra loro uguali, e questo vale anche per l’insieme unione.

Per meglio chiarire, possiamo definire l’operazione di unione tra gli insiemi {A} e {B} come un’operazione insiemistica che restituisce come risultato un insieme dato da:

• tutti gli elementi non in comune tra i due insiemi {A} e {B};
• più, tutti gli eventuali elementi in comune tra i due insiemi {A} e {B}.

Tenendo a mente questa definizione alternativa è a nostro parere più immediato evitare l’errore di ripetere nell’insieme unione uno stesso elemento. Considerati infatti gli stessi insiemi {A} e {B} abbiamo:

• elementi non in comune tra gli insiemi {A} e {B}: {1, 5, 7, 8 ,10};
• elementi in comune tra i due stessi insiemi: {3}.

A questo punto non resta che rappresentare l’insieme unione come un insieme che contiene tutti gli elementi che abbiamo sinora scritto:

A \cup B = \{ 1, 5, 7, 8,10, 3\}

Ritroviamo così lo stesso insieme unione che abbiamo scritto in precedenza (ricordiamo che l’ordine o sequenza con la quale vengono elencati gli elementi di un insieme non conta).

Esempio 2

Consideriamo i due insiemi:

\begin{align*} &\  A=\{\text{insieme dei numeri naturali pari} \}, \\ \\ & B=\{\text{insieme dei numeri naturali dispari\}} \end{align*}

Abbiamo allora:

A \cup B = \N

Infatti l’unione tra l’insieme dei numeri naturali dispari e l’insieme dei numeri naturali pari restituisce l’insieme dei numeri naturali {\N}.

Unione tra insiemi ed insieme vuoto

L’unione tra un dato insieme {A} e l’insieme vuoto ha come risultato lo stesso insieme {A}:

A \cup \emptyset = A

Ciò discende direttamente dal fatto che l’insieme vuoto è l’insieme privo di elementi.

Unione tra più di due insiemi

L’operazione di unione tra insiemi può essere estesa agevolmente al caso di tre o più insiemi.

L’insieme unione di tre o più insiemi è dato da un insieme che contiene gli elementi di tutti gli insiemi di partenza. In simboli, fissato un insieme universo {E}: {\small A_1 \cup A_2 \cup A_3 \dots \cup A_n = \{x \in E \: | \: x \in A_1 \: \vee \: x \in A_2 \: \dots \vee\: x \in A_n \}, \:n \in \N}

Così ad esempio nel caso di tre insiemi in un dato universo {E} abbiamo:

A_1 \cup A_2 \cup A_3 = \{x \in E \: | \: x\in A_1 \: \vee \: x \in A_2 \: \vee \: x \in A_3 \}

Così l’insieme unione degli insiemi {A_1, \: A_2, \: A_3} è l’insieme che contiene tutti gli elementi di ciascun insieme, compresi anche gli elementi in comune tra gli insiemi.

Unione tra insiemi e diagrammi di Venn

Consideriamo i due insiemi finiti in un dato universo {E}:

A=\{1, \: 5, \: 23\}, \qquad B=\{2,\: 4, \: 7, \: 23\}

Graficamente l’insieme unione {A \cup B} si rappresenta come segue:

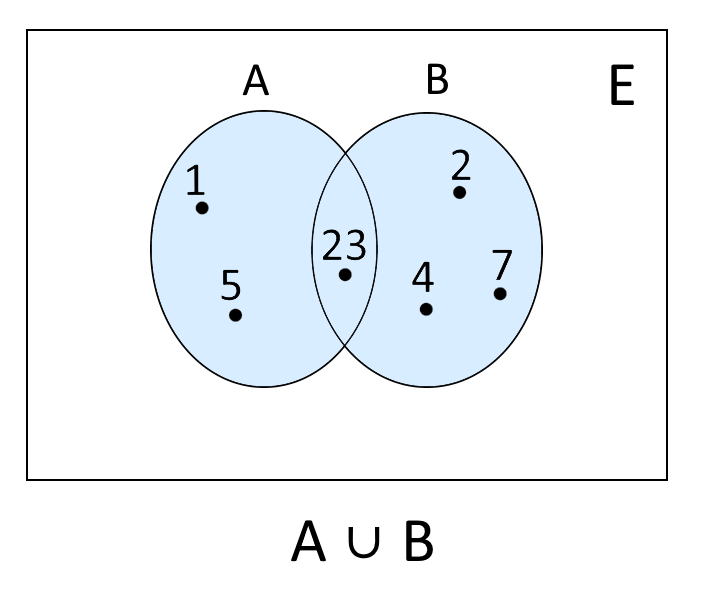
ed abbiamo:

A \cup B = \left\{ 1,2,4,5,7,23\right\}

Nella rappresentazione grafica abbiamo evidenziato l’insieme unione con il colore azzurro. E nello scrivere l’insieme unione per elencazione, come al solito non abbiamo ripetuto l’elemento {23} che è in comune ai due insiemi.

Consideriamo ora i due insiemi, fissato ancora un universo {E}:

A=\{3, \: 5, \: 9\}, \qquad B=\left\{ 4,\:6,12\right\}

Tramite l’utilizzo dei diagrammi di Venn possiamo rappresentare l’operazione di unione tra i due insiemi come segue:

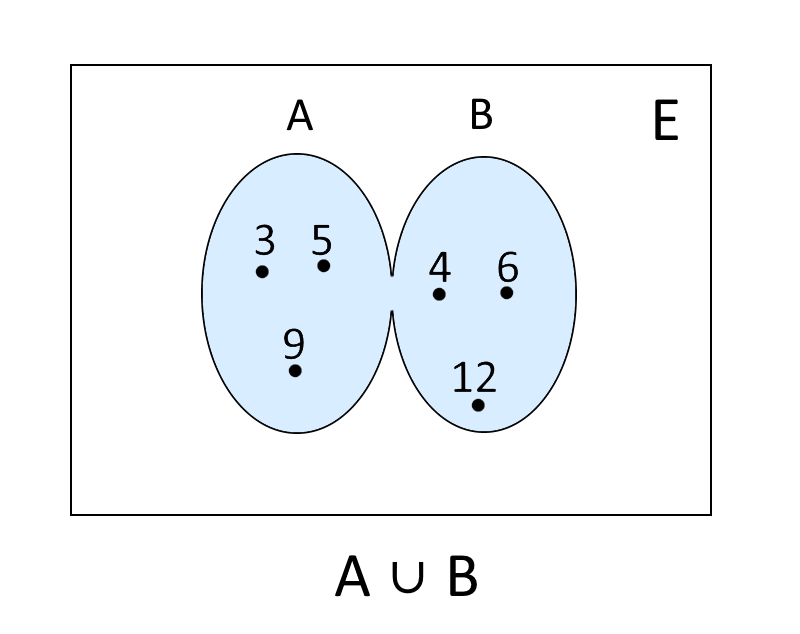
ed abbiamo:

A \cup B = \left\{ 3,4,5,6,9,12\right\}

In questo particolare caso i due insiemi di partenza non hanno elementi in comune. Per cui è sufficiente scrivere gli elementi di entrambi gli insiemi senza preoccuparsi delle ripetizioni.

Proprietà dell’operazione di unione insiemistica

Veniamo ora alle proprietà dell’operazione di unione tra insiemi. Nelle proprietà troverete anche le operazioni di intersezione tra insiemi e di complementare di un insieme, delle quali ancora non abbiamo parlato. Tuttavia, nessun problema: tratteremo questi concetti nelle lezioni successive. In ogni caso, per chi non è qui per un ripasso ma sta studiando gli insiemi per la prima volta, anticipiamo che:

• l’operazione di intersezione tra gli insiemi {A} e {B} restituisce come risultato l’insieme intersezione {A \cap B}, che contiene soltanto gli elementi in comune tra gli insiemi dati. Ci occuperemo di questa operazione nella prossima lezione;
• fissato un insieme universo {E}, il complementare di un insieme {A} rispetto all’universo {E} è l’insieme {\mathcal{C}_{E}(A)} formato da tutti gli elementi dell’insieme {E} che non appartengono ad {A}.

1) Unione di un insieme con i sottoinsiemi impropri di quello stesso insieme

Ricordiamo che dato un insieme {A}, i suoi sottoinsiemi impropri sono l’insieme stesso e l’insieme vuoto. Abbiamo:

A \cup A = A

ed inoltre, come già anticipato:

A \cup \emptyset = A

2) Proprietà commutativa dell’unione

Poiché la sequenza con cui elenchiamo gli elementi di un insieme non conta, abbiamo:

A \cup B = B \cup A

3) Proprietà associativa dell’unione

Per la proprietà associativa si ha:

A \cup (B \cup C)=(A \cup B) \cup C

4) Proprietà distributiva dell’unione rispetto all’intersezione

Tra le operazioni di unione ed intersezione tra insiemi vale la proprietà distributiva (proprietà distributiva dell’unione rispetto alla intersezione):

A \cup (B \cap C)=(A \cup B) \cap (A \cup C)

5) Complementare dell’insieme unione (legge di de Morgan dell’unione)

Il complementare dell’insieme unione rispetto ad un fissato universo {E} è uguale all’insieme intersezione del complementare dell’insieme {A} e del complementare dell’insieme {B}, sempre rispetto al fissato universo {E}:

\mathcal{C}_{E}(A \cup B)=\mathcal{C}_EA \cap C_{E}B

Per chi già conosce la logica, la precedente uguaglianza corrisponde alla legge:

\neg (p \vee q)=\neg (p) \wedge \neg(q)

ove {p} e {q} sono proposizioni logiche, {\neg} è il simbolo della negazione logica e i simboli {\vee} e {\wedge} indicano rispettivamente le operazioni di disgiunzione logica inclusiva (l’analoga dell’unione insiemistica) e di congiunzione logica (l’analoga dell’intersezione insiemistica).

6) Unione di un insieme con il suo complementare

Per la definizione di insieme complementare rispetto ad un fissato insieme universo {E} si ha:

B \cup \mathcal{C}_E(B)=E

7) Unione di un insieme con l’insieme universo

Fissati un insieme {A} e l’insieme universo {E}:

A \cup E = E

8) Unione di un insieme con un suo sottoinsieme

Se si ha che {B \subseteq A}, allora possiamo scrivere:

A \cup B = A

L’unione di un insieme con un suo sottoinsieme restituisce sempre il sovrainsieme (ovvero l’insieme più grande dei due).

Osservazione. Le proprietà {7} e {8} rappresentano in pratica la stessa proprietà. Infatti, con riferimento alla proprietà {7}, per definizione l’insieme universo {E} scelto è un sovrainsieme dell’insieme {A} (ovvero l’insieme {E} contiene l’insieme {A}). Allo stesso modo, con riferimento alla proprietà {8}, l’insieme {A} è un sovrainsieme dell’insieme {B} (ovvero {A} contiene {B}). Ed in entrambi i casi, il risultato dell’operazione di unione tra i due rispettivi insiemi è l’insieme più grande (il sovrainsieme).

9) Sottoinsiemi dell’insieme unione

Abbiamo:

A \subseteq (A \cup B), \qquad B \subseteq (A \cup B)

In altre parole, entrambi gli insiemi {A} e {B} sono sottoinsiemi dell’insieme dato dalla loro unione.

Per questa lezione è tutto. Nella prossima lezione ci occuperemo dell’operazione di intersezione tra insiemi. Buon proseguimento! 🙂