Come si calcola il volume del cilindro? Potreste fornire degli esercizi svolti, indicando le formule da utilizzare in base ai dati di partenza disponibili?
Per calcolare il volume del cilindro dobbiamo moltiplicare l’area di base del cilindro per la sua altezza. E dato che la base di un cilindro è un cerchio, l’area di base si ottiene moltiplicando il quadrato del raggio di base del cilindro per la costante Pi Greco. Di conseguenza, il volume sarà dato anche dal quadrato del raggio di base, moltiplicato per Pi Greco e per l’altezza della figura.
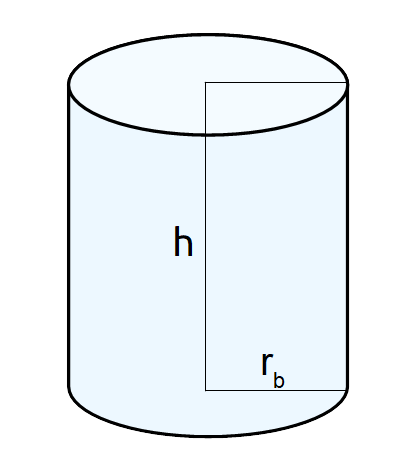
Così intanto per il volume del cilindro abbiamo le due seguenti formule:
V=S_b \cdot h; \qquad V= \pi \cdot r_{b}^2 \cdot hove {V} è il volume del cilindro, {S_b} è la superficie di base, {h} è l’altezza del cilindro, {r_b} il raggio di base del cilindro (il raggio del cerchio base del cilindro) e {\pi} è il numero fisso o costante Pi Greco. In questi casi possiamo prendere per Pi Greco l’approssimazione {3,14} (se si vuole più precisione, {3,14159} è un’approssimazione adeguata un po’ per tutti i casi).
La superficie laterale del cilindro è data da:
S_l =2 \cdot \pi \cdot r_b \cdot h =C \cdot h
ovvero è il prodotto della circonferenza di base del cilindro (perimetro di base) per la sua altezza. Osserviamo che disponendo del raggio di base o dell’altezza del cilindro e della superficie laterale è possibile calcolare il volume del cilindro.
A partire dalla superficie laterale e dal raggio di base abbiamo:
h = \dfrac{S_l}{2 \cdot \pi \cdot r_b}; \qquad V =\pi \cdot r_b^2 \cdot hovvero è possibile calcolare l’altezza del cilindro a partire dalla superficie laterale e dal raggio di base, in modo da poter poi procedere al calcolo del volume del cilindro stesso.
In modo del tutto simile è possibile ricavare il volume del cilindro a partire dalla superficie laterale e dall’altezza:
r_b = \dfrac{S_l}{2 \cdot \pi \cdot h}; \qquad V = \pi \cdot r_b^2 \cdot hSe invece disponiamo come dati di partenza del perimetro di base (circonferenza del cerchio di base) e dell’altezza del cilindro possiamo ricavare il raggio di base e quindi calcolare il volume:
r_b = \dfrac{C}{2 \cdot \pi }; \qquad V =\pi \cdot r_b^2 \cdot hInfine, ricordiamo che la superficie totale del cilindro è data da:
S_{tot} = S_l + 2 \cdot S_bPer cui ad esempio se abbiamo come dati di partenza la superficie totale del cilindro e il raggio di base, possiamo ricavare il volume del cilindro. Cominciamo anzitutto ricavando la superficie di base e da essa la superficie laterale:
S_b = \pi \cdot r_b^2 ; \qquad S_l=S_{tot} - 2 \cdot S_bA questo punto dalla superficie laterale possiamo ricavare l’altezza del cilindro:
h= \dfrac{S_l}{C}Infine calcoliamo il volume:
V = S_b \cdot h
Fatta una panoramica sulle varie formule relative al calcolo del volume del cilindro, vediamo degli esercizi di esempio che ne mostrano il pratico uso.
Esercizi di esempio sul calcolo del volume del cilindro
Volume del cilindro a partire dalla superficie di base e dall’altezza
Esempio 1
Calcolare il volume di un cilindro avente superficie di base pari a {78,54 \text{cm}^2} e altezza pari a {10 \text{cm}}.
Abbiamo:
V= S_b \cdot h = 78,54 \text{cm}^2 \cdot 10 \text{cm} = 785,4 \text{cm}^3Volume del cilindro a partire dal raggio di base e dall’altezza
Esempio 2
Calcolare il volume di un cilindro avente raggio di base pari a {4 \text{cm}} e altezza uguale a {15 \text{cm}}.
Cominciamo calcolando la superficie di base:
S_b = \pi \cdot r_b^2 = 3,14 \cdot (4 \text{cm})^2=3,14 \cdot 16 \text{cm}^2=50,24 \text{cm}^2A questo punto possiamo calcolare il volume:
V= S_b \cdot h = 50,24 \text{cm}^2 \cdot 15 \text{cm} = 753,6 \text{cm}^3Dati di partenza: superficie laterale e dal raggio di base
Esempio 3
Un cilindro ha superficie laterale pari a {120 \text{cm}^2} e raggio di base pari a {8 \text{cm}}. Calcolare il volume.
Dalla superficie laterale possiamo ricavare l’altezza del cilindro:
h = \dfrac{S_l}{2 \cdot \pi \cdot r_b} =\dfrac{120 \text{cm}^2}{2 \cdot 3,14 \cdot 8 \text{cm}}= 2,39 \text{cm}Per il volume abbiamo così:
V= \pi \cdot r_b^2 \cdot h = 3,14 \cdot (8 \text{cm})^2 \cdot 2,39 \text{cm} \approx 480,29 \text{cm}^3Dati di partenza: superficie laterale e dalla altezza
Esempio 4
Un cilindro ha superficie laterale pari a {120 \text{cm}^2} e altezza pari a {2,4 \text{cm}}. Calcolare il volume.
Ricaviamo il raggio di base a partire dalla superficie laterale:
r_b = \dfrac{S_l}{2 \cdot \pi \cdot h}=\dfrac{120 \text{cm}^2}{2 \cdot 3,14 \cdot 2,4 \text{cm}}=7,96 \text{cm}e quindi per il volume:
V= \pi \cdot r_b^2 \cdot h=3,14 \cdot (7,96 \text{cm})^2 \cdot 2,4 \text{cm} \approx 477,49 \text{cm}^3Volume del cilindro a partire dalla superficie totale e dal raggio di base
Esempio 5
Sia dato un cilindro di superficie totale {227 \text{cm}^2} e avente raggio di base uguale a {5,6 \text{cm}}. Calcolare il volume.
Cominciamo calcolando la superficie di base:
S_b = \pi \cdot r_b^2 = 3,14 \cdot (5,6 \text{cm})^2 = 98,47 \text{cm}^2La superficie laterale è data da:
S_l = S_{tot}-2 \cdot S_b = (227- 2 \cdot 98,47) \text{cm}^2 = 30,06 \text{cm}^2Ricaviamo a questo punto l’altezza del cilindro (disponiamo infatti sia della superficie laterale, sia del raggio di base):
h = \dfrac{S_l}{\underbrace{2 \cdot \pi \cdot r_b}_{C}}=\dfrac{30,06 \text{cm}^2}{2 \cdot 3,14 \cdot 5,6 \text{cm}}= \dfrac{30,06 \text{cm}^2}{35,168 \text{cm}} \approx 0,85 \text{cm}Ovviamente avremmo anche potuto calcolare separatamente la circonferenza di base, ricavando poi l’altezza.
Concludiamo calcolando il volume:
V= S_b \cdot h = 98,47 \text{cm}^2 \cdot 0,85 \text{cm} \approx 83,70 \text{cm}^3Cilindro equilatero
Un cilindro equilatero è un particolare cilindro avente altezza uguale al doppio del raggio di base. Per il calcolo del volume abbiamo:
V = \pi \cdot r_b^2 \cdot h \quad \text{con} \quad h= 2 \cdot r_b \quad \Rightarrow \quad V = \pi \cdot r_b ^2 \cdot 2 \cdot r_b e quindi:
\boxed{V=2 \cdot \pi \cdot r_b^3}Inoltre, poiché il raggio di base è uguale alla metà dell’altezza del cilindro, vale anche la seguente formula:
V = \pi \cdot r_b^2 \cdot h \quad \text{con} \quad r_b = \dfrac{h}{2} \quad \Rightarrow \quad V = \pi \cdot \dfrac{h^2}{4} \cdot h e quindi:
\boxed{V = \dfrac{\pi \cdot h^3}{4}}Vediamo subito un paio di esempi.
Esempio 6
Un cilindro equilatero ha raggio di base uguale a {7 \text{cm}}. Calcolare il volume.
Abbiamo:
V = 2 \cdot \pi \cdot r_b^3 = 2 \cdot 3,14 \cdot (7 \text{cm})^3 = 2 \cdot 3,14 \cdot 343 \text{cm}^3 = 2.154,04 \text{cm}^3Esempio 7
Un cilindro equilatero ha altezza pari a {10 \text{cm}}. Calcolare il volume.
Si ha:
V= \dfrac{\pi \cdot h^3}{4}= \dfrac{3,14 \cdot (10 \text{cm})^3}{4}=785 \text{cm}^3| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
