Calcolare il diametro dalla circonferenza

 - 

Domande e risposte

Come si può calcolare il diametro di un cerchio a partire dalla sua circonferenza? E a partire dall’area del cerchio? Potrei avere una spiegazione delle formule con relativi esempi di applicazione?

Per calcolare il diametro di un cerchio a partire dalla sua circonferenza basta dividere la misura della circonferenza stessa per il numero fisso (o costante) {\pi}.

Diversamente, per calcolare il diametro di un cerchio a partire dall’area della circonferenza (o meglio area del cerchio) basta dividere il quadruplo dell’area per la costante {\pi} e quindi estrarre la radice quadrata del risultato ottenuto.

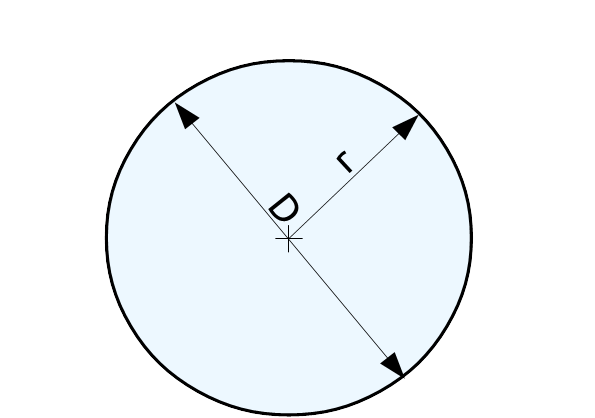
Come in figura, indichiamo con {D} il diametro della circonferenza (da non confondersi con il raggio {r}, la cui misura è pari alla metà del diametro). Indichiamo inoltre con {A} l’area del cerchio e con {\pi} una particolare costante o numero fisso, approssimabile nei casi più semplici con il valore {3,14}. Infine, indichiamo con {C} la misura della circonferenza del cerchio.

Calcolare il diametro di un cerchio a partire dalla misura della sua circonferenza e dall’area

Ricordiamo la formula che esprime la circonferenza di un cerchio in funzione del suo diametro:

C=\pi \cdot D

Dividendo entrambi i membri dell’uguaglianza per {\pi}:

\dfrac{C}{\pi}=\dfrac{\cancel{\pi} \cdot D}{\cancel{\pi}}

da cui otteniamo la formula per calcolare il diametro di un cerchio a partire dalla sua circonferenza:

\boxed{D = \dfrac{C}{\pi}}

Ricordiamo inoltre la formula per il calcolo dell’area del cerchio a partire dal diametro:

A=\pi \cdot \dfrac{D^2}{4}

La formula si ricava facilmente dalla più semplice formula che esprime l’area del cerchio in funzione del raggio:

A= \pi \cdot r^2

data dal prodotto della costante {\pi} per il quadrato del raggio.

Infatti, poiché {r = \dfrac{D}{2}}abbiamo:

A=\pi \cdot  r^2=\pi \cdot \left( \dfrac{D}{2}\right)^2 = \pi \cdot  \dfrac{D^2}{4}

e quindi:

{ A =  \dfrac{\pi \cdot D^2}{4}}

Grazie a questa formula possiamo esprimere il diametro in funzione dell’area:

\boxed{D= \sqrt{\dfrac{4 \cdot A}{\pi}}}

Vediamo come ricavare quest’ultima formula a partire dalla precedente. Ripartiamo allora dalla formula:

{ A =  \dfrac{\pi \cdot D^2}{4}}

Il nostro obiettivo è isolare il diametro {D}, ovvero ritrovare il solo diametro {D} in un membro dell’uguaglianza. Cominciamo moltiplicando entrambi i membri per {4}:

A \cdot 4 =\dfrac{\pi \cdot D^2}{\cancel{4}} \cdot \cancel{4}; \qquad 4 \cdot A = \pi \cdot D^2

Ora dividiamo entrambi i membri dell’ultima uguaglianza appena scritta per {\pi}:

\dfrac{4 \cdot A}{\pi}= \dfrac{\cancel{\pi} \cdot D^2}{\cancel{\pi}}; \qquad \dfrac{4 \cdot A}{\pi}= D^2

Infine, estraiamo la radice quadrata di entrambi i membri, tenendo conto che un diametro può soltanto essere positivo:

\sqrt{\dfrac{4 \cdot A}{\pi}}=\sqrt{D^2}

E poiché per l’ipotesi detta {\sqrt{D^2}=D} otteniamo in conclusione:

\boxed{D = \sqrt{\dfrac{4 \cdot A}{\pi}}}

e questa è la formula per ricavare il diametro di una circonferenza a partire dalla sua area.

Vediamo ora subito un paio di esempi su come calcolare il diametro di un cerchio a partire dalla circonferenza oppure dall’area del cerchio.

Esempio 1

Calcolare il diametro di un cerchio avente misura della circonferenza pari a {157 \text{cm}}.

Ricaviamo il diametro dalla circonferenza dividendo la circonferenza stessa per la costante {\pi}, che come ricordato possiamo in questi semplici esercizi approssimare con il valore {3,14}. Abbiamo:

D=\dfrac{C}{\pi}=\dfrac{157 \text{cm}}{3,14}=50 \text{cm}

Esempio 2

Calcolare il diametro di un cerchio avente area {235,5 \text{mm}^2}.

Utilizzando la formula esposta in precedenza per il calcolo del diametro a partire dall’area del cerchio abbiamo:

\begin{align*} & D= \sqrt{\dfrac{4 \cdot A}{\pi}}=\sqrt{\dfrac{4 \cdot 235,5 \text{mm}^2}{3,14}}= \sqrt{\dfrac{942 \text{mm}^2}{3,14}}= \\ \\ & =\sqrt{300\text{mm}^2}\approx 17,32 \text{mm} \end{align*}

Per quanto riguarda formule ed esempi per calcolare l’area del cerchio a partire dalla circonferenza e dall’area è tutto. Buon proseguimento con SìMatematica!