In questa lezione vediamo la regola per la riduzione di radicali allo stesso indice. In altre parole, a partire da due o più radicali vedremo come scrivere dei nuovi radicali equivalenti a quelli di partenza ma aventi tutti lo stesso indice.
Saper effettuare la riduzione di radicali allo stesso indice è importante per poter poi eseguire la moltiplicazione di radicali con indice diverso tra loro. Infatti, per moltiplicare tra loro ad esempio due radicali con indice differente basterà ridurli allo stesso indice, e quindi eseguire la moltiplicazione secondo la regola del prodotto fra radicali con lo stesso indice, già vista in precedenza.
Vediamo allora subito come si effettua la riduzione di radicali allo stesso indice.
Riduzione dei radicali allo stesso indice (caso numerico)
Una conseguenza importante della proprietà invariantiva dei radicali è la possibilità di riscrivere due radicali di modo che abbiano lo stesso indice. Dati due radicali desideriamo cioè individuare due nuovi radicali aventi lo stesso valore dei radicali di partenza ma tali da avere lo stesso indice. Tale operazione si chiama riduzione dei radicali allo stesso indice.
Consideriamo i due radicali:
\sqrt[3]{2}; \qquad \sqrt[4]{7}Moltiplichiamo per {4} l’indice della radice e l’esponente del radicando relativi al primo radicale. Moltiplichiamo invece per {3} ancora l’indice della radice e l’esponente del radicando relativi stavolta al secondo radicale. Abbiamo:
\sqrt[3]{2}= \sqrt[3 \cdot 4]{2^{1 \cdot 4}}=\boxed{\sqrt[12]{2^4}}; \qquad \sqrt[4]{7}=\sqrt[4 \cdot 3]{7^{1 \cdot 3}}= \boxed{\sqrt[12]{7^3}}I due radicali ottenuti hanno lo stesso indice.
Osserviamo che abbiamo moltiplicato indice della radice ed esponente del radicando in ciascun radicale per il rapporto tra il minimo comune multiplo degli indici dei radicali di partenza e l’indice di ciascun radicale.
In base ai ragionamenti fatti ricaviamo la seguente regola pratica:
E’ possibile ridurre due o più radicali con radicando positivo allo stesso indice utilizzando come indice comune il minimo comune multiplo degli indici e moltiplicando l’esponente di ciascun radicando per il rapporto tra l’indice comune e l’indice presente nel radicando di partenza considerato.
Quando possibile, prima di ridurre i radicali allo stesso indice è consigliabile effettuare la semplificazione di ciascuno dei radicali. Infatti questa operazione consente in generale di alleggerire i calcoli successivi.
Consideriamo ad esempio i seguenti tre radicali:
\sqrt[3]{2^5}; \quad \sqrt{3^7}; \quad \sqrt[12]{5^2}I primi due radicali sono irriducibili. E’ invece possibile semplificare il terzo radicale:
\sqrt[12]{5^2}=\sqrt[12:2]{5^{2:2}}=\sqrt[6]{5}Così tenendo conto della forma semplificata appena ottenuta ci ritroviamo a dover ridurre allo stesso indice i seguenti radicali:
\sqrt[3]{2^5}; \quad \sqrt{3^7}; \quad \sqrt[6]{5}Gli indici dei radicali sono rispettivamente {3, 2} e {6}. Il minimo comune multiplo degli indici è {\text{mcm}{(3, 2, 6)=6}}.
Calcoliamo ora le quantità per le quali l’esponente del radicando relative a ciascun radicale. Come detto dobbiamo dividere il minimo comune multiplo degli indici per l’indice di ciascun radicale:
6:3=2; \qquad 6:2 = 3; \qquad 6:6 = 1
A questo punto utilizziamo {6} come indice comune e moltiplichiamo l’esponente del radicando di ciascun radicale per le rispettive quantità appena determinate:
\begin{align*} & \sqrt[3]{2^5}=\sqrt[6]{2^{5 \cdot 2}}= \boxed{\sqrt[6]{2^{10}}}; \\ \\ &\sqrt{3^7}=\sqrt[6]{3^{7 \cdot 3}}=\boxed{\sqrt[6]{3^{21}}}; \\ \\ & \sqrt[6]{5}=\sqrt[6 ]{5^{1 \cdot 1}}=\boxed{\sqrt[6]{5}} \end{align*}Osserviamo che i radicali evidenziati sono tutti equivalenti a quelli di partenza ed hanno tutti lo stesso indice. Abbiamo quindi ridotto i radicali dati allo stesso indice.
Nel caso dei radicali con indice dispari e radicando negativo vale la seguente regola.
Se fra i radicali da ridurre allo stesso indice ci sono uno o più radicali con indice dispari e radicando negativo, occorre in tali radicali portare fuori il segno meno per poi procedere alla riduzione allo stesso indice come da regola precedente.
Così ad esempio per ridurre allo stesso indice i seguenti radicali:
\sqrt[3]{-9}; \qquad \sqrt{5}; \qquad \sqrt[5]{-2^3}dovremo prima di tutto portare fuori il segno meno dai radicali aventi radicando negativo:
\sqrt[3]{-9}=-\sqrt[3]{9}; \qquad \sqrt[5]{-2^3}=-\sqrt[5]{2^3}Così dovremo ridurre allo stesso indice i seguenti radicali:
-\sqrt[3]{9}=-\sqrt[3]{3^2}; \qquad \sqrt{5}; \qquad -\sqrt[5]{2^3}Ma a questo punto non resta che procedere con le regole già viste. Il minimo comune multiplo degli indici è {30}, per cui riducendo i radicali a questo indice comune otteniamo:
-\sqrt[30]{3^{20}}; \qquad \sqrt[30]{{5^{15}}}; \qquad -\sqrt[30]{2^{18}}Giustificazione della regola per la riduzione di radicali allo stesso indice.
Riprendiamo i tre radicali di partenza relativi al penultimo esempio, per comodità nella forma già semplificata:
\sqrt[3]{2^5}; \quad \sqrt{3^7}; \quad \sqrt[6]{5}Riscriviamoli come potenze con esponente frazionario:
2^{\frac{5}{3}}; \qquad 3^{\frac{7}{2}}; \qquad 5^{\frac{1}{6}}Poiché l’indice di ciascun radicale è uguale al denominatore della corrispondente potenza ad esponente frazionario, per ridurre i radicali di partenza allo stesso indice basterà calcolare il denominatore comune delle frazioni all’esponente nelle potenze appena scritte. In tal modo potremo ridurre a denominatore comune tutte le frazioni ad esponente. Abbiamo:
\text{mcm} (3, 2 , 6) = 6, \qquad \text{denominatore comune} Le frazioni agli esponenti diventano, riducendole allo stesso denominatore comune {6}:
\begin{align*} & \dfrac{5}{3} \quad \Rightarrow \quad \dfrac{\overbrace{(6:3)}^{2} \cdot 5}{\underbrace{6}_{3 \cdot 2}}=\dfrac{10}{6}; \\ \\ & \dfrac{7}{2} \quad \Rightarrow \quad \dfrac{\overbrace{(6:2)}^{3} \cdot 7 }{\underbrace{6}_{2 \cdot 3}} = \dfrac{21}{6} \\ \\ & \dfrac{1}{6} \quad \Rightarrow \quad \dfrac{1}{6}\end{align*}Osserviamo che in pratica abbiamo moltiplicato numeratore e denominatore di ciascuna frazione di partenza per uno stesso numero. Quindi, abbiamo applicato la proprietà invariantiva della divisione.
Ora, come sappiamo mettendo delle frazioni a denominatore comune otteniamo delle nuove frazioni equivalenti a quelle di partenza. Di conseguenza, le seguenti potenze corrisponderanno agli stessi valori delle potenze di partenza:
2^{\frac{10}{6}}; \qquad 3^{\frac{21}{6}}; \qquad 5^{\frac{1}{6}}Per concludere non resta che riscrivere tali potenze sotto forma di radicali (il denominatore dell’esponente è l’indice, il numeratore è l’esponente del radicando):
\sqrt[6]{2^{10}}; \qquad \sqrt[6]{3^{21}}; \qquad \sqrt[6]{5}Abbiamo ritrovato gli stessi radicali ottenuti con la regola pratica. Di conseguenza, la regola per la riduzione di radicali allo stesso indice si giustifica con la proprietà invariantiva della divisione.
Riduzione di radicali allo stesso indice nel caso di radicando variabile
Nel caso di radicando variabile, per ridurre dei radicali allo stesso indice occorre anzitutto determinare l’insieme {D} delle {x} ove tutti i radicali esistono. Quindi, bisogna procedere studiando il segno di ciascun radicale in detto insieme. In tal modo, potremo attribuire i segni ai nuovi radicali che scriveremo in base al valore della variabile.
Esempio 1
Ridurre allo stesso indice i radicali:
\sqrt{x+1}; \qquad \sqrt[3]{x-1}; \qquad \sqrt[3]{x}Determiniamo per prima cosa l’insieme di definizione comune a tutti e tre i radicali. Il primo radicale, avente indice pari, esiste per {x+1 \geq 0}, ovvero per {x \geq -1}. Gli altri due radicali esistono invece per ogni {x} reale. Infatti questi ultimi hanno indice dispari.
Di conseguenza, l’insieme di definizione {D} relativo a tutti e tre i radicali è {x \geq -1} (l’intersezione degli insiemi di esistenza dei singoli radicali).
Ora vediamo cosa succede relativamente ai segni nell’insieme {D}. Il primo radicale è positivo o al più nullo per ogni {x} dell’insieme {D}. Quindi:
\sqrt{x+1} \geq 0 \qquad \forall \: x \geq -1Per quanto riguarda il secondo radicale, studiamo il segno al variare di {x} in {\mathbb{R}} e quindi vediamo che segno assume nell’insieme {D}.
Abbiamo {x-1 \geq 0 } per {x \geq 1}. Quindi il radicale {\sqrt{x+1}} è positivo o nullo in {\mathbb{R}} e nell’insieme {D} per ogni {x} maggiore o uguale a {1}.
Viceversa, il radicale risulterà negativo in {\mathbb{R}} per ogni {x < 1}. Tuttavia, dobbiamo considerare i soli valori della {x} dell’insieme {D}. Dovremo quindi effettuare l’intersezione tra l’insieme delle {x} in {\mathbb{R}} ove il radicale è negativo e l’insieme delle {x} che appartengono a {D}:
\begin{cases} x < 1 \\ \\ x \geq -1\end{cases} \quad \Rightarrow \quad -1 \leq x<1Quindi per {-1 \leq x<1} il radicale {\sqrt[3]{x-1}} è negativo in {D}.
Infine, in modo del tutto simile per il segno in {D} del terzo radicale abbiamo:
\sqrt[3]{x} < 0 \iff -1 \leq x < 0 ; \qquad \sqrt[3]{x} \geq 0 \iff x \geq 0 Se più comodo, possiamo in alternativa effettuare lo studio dei segni dei radicali per via grafica, escludendo i valori che non appartengono a {D}:
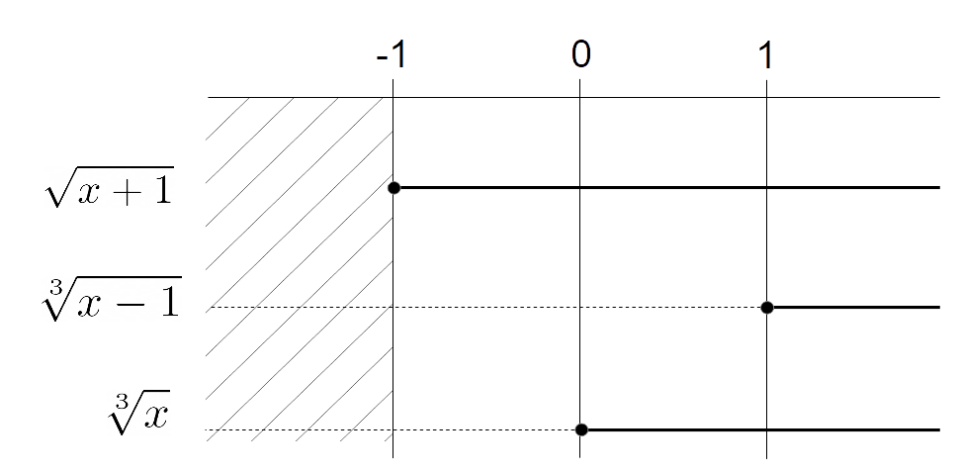
A questo punto prendiamo il minimo comune multiplo degli indici dei radicali:
\text{mcm}(2,3,3) = 6Ora non resta che riscrivere i radicali di partenza come radicali ad essi equivalenti aventi indice {6}, prestando attenzione al segno ove necessario.
Il primo radicale di partenza ha indice pari. Anche il nuovo radicale corrispondente avrà indice pari, per cui in questo caso non dobbiamo imporre alcuna condizione e possiamo scrivere direttamente:
\sqrt{x+1} = \sqrt[2 \cdot 3]{(x+1)^{1 \cdot 3}}=\sqrt[6]{(x+1)^3}Gli altri due radicali di partenza hanno invece indice dispari. Dovendo riscriverli con indice {6}, quindi pari, dobbiamo prestare attenzione ai segni. In particolare, dovremo mettere un segno meno davanti al nuovo radicale per i valori della {x}per i quali il corrispondente radicale di partenza è negativo in {D}, e mettere un segno più davanti al radicale per i valori per i quali il radicale di partenza corrispondente è invece positivo in {D}:
\sqrt[3]{x-1}= \begin{cases} -\sqrt[6]{(x-1)^2} \quad \text{per} \quad -1 \leq x < 1 \\ \\ \sqrt[6]{(x-1)^2} \quad \text{per} \quad x \geq 1 \end{cases}Analogamente abbiamo per il terzo radicale:
\sqrt[3]{x}= \begin{cases} -\sqrt[6]{x} \quad \text{per} \quad -1 \leq x < 0 \\ \\ \sqrt[6]{x} \quad \text{per} x \geq 0 \end{cases}Abbiamo così ridotto i radicali di partenza allo stesso indice.
Conclusioni
Per questa lezione sulla riduzione dei radicali allo stesso indice è tutto. Precisiamo soltanto come ultima nota che quanto appreso nella lezione è anche utile per confrontare dei radicali tra loro. Ad esempio, supponiamo di voler stabilire a quale tra i due seguenti radicali corrisponde il valore maggiore, senza usare la calcolatrice:
\sqrt[3]{3^4}; \qquad \sqrt[4]{3^6}Basta ridurre i radicali allo stesso indice, e quindi confrontare i radicandi:
\sqrt[3 \cdot 4]{3^{4 \cdot 4}}= \sqrt[12]{3^{16}}; \qquad \sqrt[4 \cdot 3]{3^{6 \cdot 3}}=\sqrt[12]{3^{18}}Poiché {3^{18} > 3^{16}} concludiamo che il secondo radicale è quello al quale corrisponde il valore maggiore:
\sqrt[12]{3^{18}} > \sqrt[12]{3^{16}}Nella prossima lezione ci occuperemo del prodotto e quoziente di radicali con indici diversi. Buon proseguimento!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
