Come si calcola l’area del rombo? Quali formule devo utilizzare per trovare l’area del rombo e di quali dati ho bisogno?
Per calcolare l’area del rombo, il metodo più comune consiste nel moltiplicare tra loro le misure delle due diagonali del rombo, dividendo il risultato ottenuto per {2}.
Tuttavia, è possibile calcolare l’area del rombo anche disponendo di altri dati. Di conseguenza, le formule per trovare l’area del rombo sono più di una.
Formule per calcolare l’area del rombo
Il rombo è un particolare parallelogramma che presenta la proprietà di avere i lati tutti uguali (congruenti).

Così tutti e quattro i lati del rombo hanno la stessa misura {L}. Per ciascun lato avremo una relativa altezza {h} corrispondente al vertice opposto al lato. Ad esempio, l’altezza relativa al lato {L} in figura è un segmento tracciato a partire del vertice opposto allo stesso lato e tale da essere perpendicolare al medesimo lato {L}. Tra parentesi, le altezze possono anche essere costruite a partire da un vertice fino ad arrivare al prolungamento del lato opposto al vertice. Così in tutto nel rombo abbiamo otto altezze, tutte di uguale misura.
Le diagonali nel rombo sono tra loro perpendicolari ed in generale hanno misura differente ({d_1} e {d_2} in figura). Nel caso in cui la due perpendicolari abbiano la stessa misura otteniamo un quadrato.
In figura è inoltre rappresentata la circonferenza inscritta al rombo, avente raggio {r}.
In base ai dati che abbiamo a disposizione esistono differenti formule per calcolare l’area del rombo.
- se come dati di partenza abbiamo le misure delle due diagonali utilizzeremo la formula:
{A = \dfrac{d_1 \cdot d_2}{2}} - se invece disponiamo della misura {L} dei lati del rombo e dell’altezza {h} utilizzeremo la formula: {A = L \cdot h}
- infine, se come dati di partenza abbiamo la misura del raggio della circonferenza inscritta al rombo e la misura dei lati del rombo utilizzeremo la formula: {A= L \cdot 2r}
La terza formula si giustifica a partire dalla seconda poiché in un rombo {h= 2\cdot r}. L’altezza di un rombo è cioè uguale al doppio del raggio della circonferenza inscritta nel rombo stesso.
Le prime due formule si possono giustificare graficamente.
Per la prima formula, consideriamo la seguente figura:
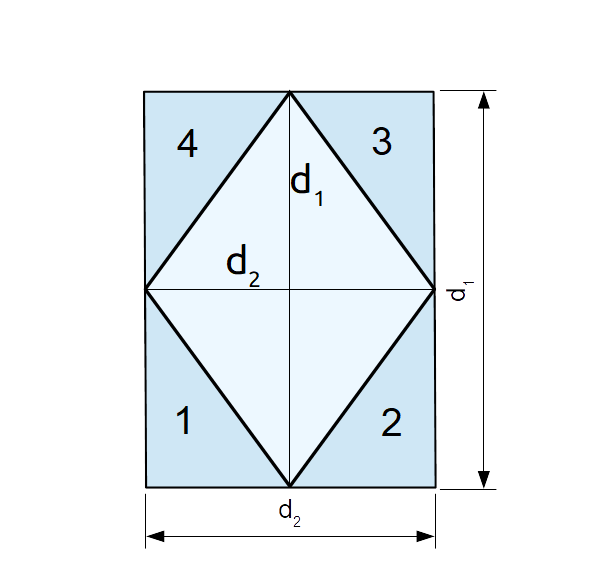
Abbiamo qui circoscritto al rombo un rettangolo avente base ed altezza di misure corrispondenti a quelle delle diagonali del rombo.
Osserviamo che le somme delle aree dei triangoli rettangoli 1, 2, 3 e 4 sono uguali all’area del rombo. Di conseguenza, il rettangolo avrà area doppia di quella del rombo. E poiché l’area del rettangolo è pari al prodotto della base per l’altezza, ovvero {d_1 \cdot d_2}, l’area del rombo sarà uguale a {\dfrac{d_1 \cdot d_2}{2}}.
Per la seconda formula, osserviamo la seguente figura:
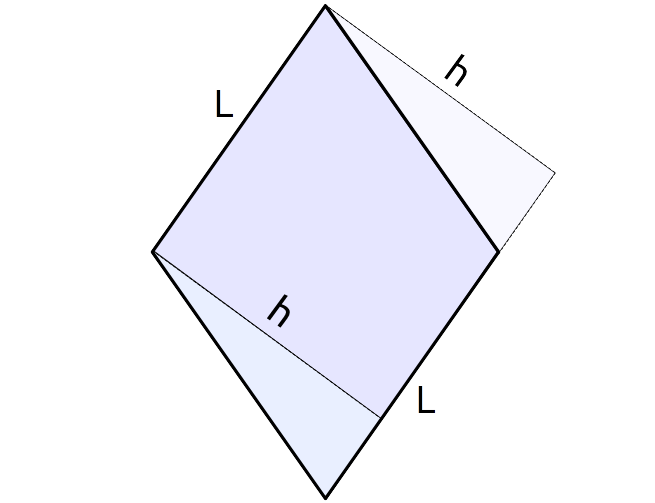
Possiamo immediatamente notare che abbiamo due triangoli rettangoli aventi la stessa area. Di conseguenza, l’area del rettangolo di lati {L} e {h} è uguale all’area del rombo.
Esercizi di esempio sul calcolo dell’area del rombo
Esempio 1
Calcolare l’area di un rombo avente diagonale minore di misura {10 \text{cm}} e diagonale maggiore il triplo della minore.
Indichiamo ad esempio con {d_2} la diagonale minore. Per cui come dato di partenza abbiamo {d_2 = 10 \text{cm}}. Per quanto ci dice il testo dell’esercizio:
d_1 = 3 \cdot d_2 = 3 \cdot 10 \text{cm} = 30 \text{cm}Per cui utilizzando la prima formula:
A= \dfrac{d_1 \cdot d_2}{2} = \dfrac{30 \text{cm} \cdot 10 \text{cm}}{2} = 150 \text{cm}^2Esempio 2
Calcolare l’area di un rombo avente altezza {35 \text{cm}} e lato {20 \text{cm}}.
Abbiamo (seconda formula):
A= L \cdot h = 20 \text{cm} \cdot 35 \text{cm} = 700 \text{cm}^2Esempio 3
Calcolare l’area di un rombo avente lato {2 \text{m}} e raggio della circonferenza inscritta {1,3 \text{m}}.
Come dati di partenza abbiamo ila misura dei lati del rombo e il raggio della circonferenza inscritta. Utilizziamo allora la terza formula:
A = L \cdot 2 \cdot r = 2 \text{m} \cdot 2 \cdot 1,3 \text{m} = 5,2 \text{m}^2Area con la misura dei lati e il seno di un angolo interno
Ricorrendo alla trigonometria è anche possibile calcolare l’area di un rombo a partire dalla misura dei suoi lati e il seno trigonometrico di uno qualsiasi dei suoi angoli interni. Precisiamo che l’angolo interno di un rombo è un angolo compreso tra due lati qualsiasi del rombo.
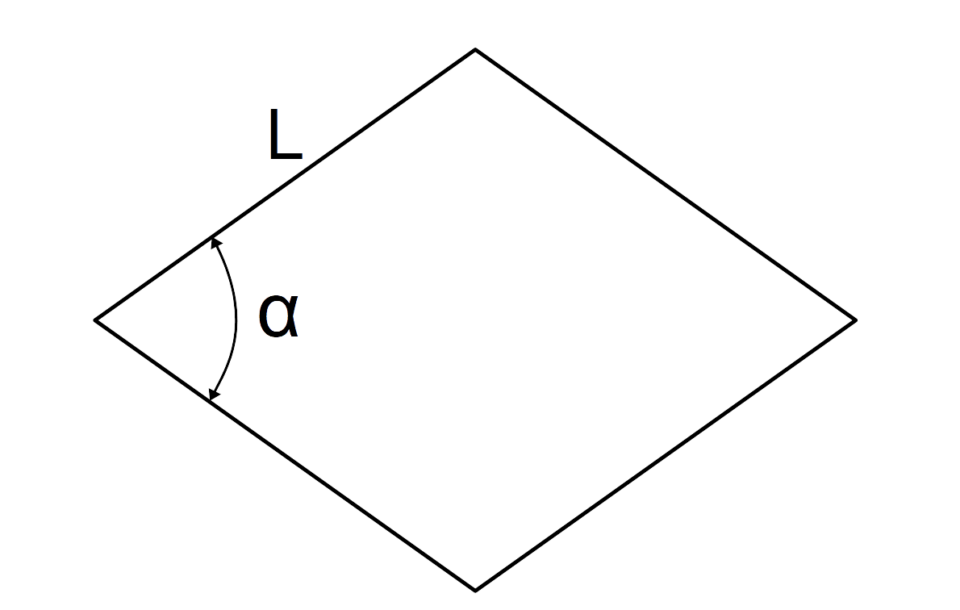
In particolare, a partire da questi dati di partenza, l’area del rombo è uguale al prodotto tra il quadrato della misura di un lato del rombo e il seno dell’angolo {\alpha}:
A= L^2 \cdot \sin \alpha
Esempio
Se i lati di un rombo hanno misura {100 \text{cm}} e l’angolo compreso tra due lati è pari a {27°}, abbiamo:
A=L^2 \cdot \sin \alpha = (100 \text{cm})^2 \cdot \sin (27°)=4540 \text{cm}^2Per il calcolo del valore della funzione seno attenzione ad impostare correttamente i gradi come unità di misura degli angoli nella calcolatrice. Ricordiamo in particolare che i gradi sessagesimali sono indicati con la sigla {\text{DEG}}. Attenzione a non impostare la calcolatrice su {\text{GRAD}}. Questi sono infatti i gradi centesimali e vengono usati solo raramente.
Se per i calcoli trigonometrici la vostra calcolatrice è impostata in radianti, senza alterare alcuna impostazione è possibile convertire l’angolo dai gradi ai radianti. Nel nostro caso basterà impostare la proporzione:
\pi : 180° = x:27°
da cui otteniamo la misura dell’angolo dato espresso in radianti:
x = \dfrac{\pi \cdot 27°}{180°} \approx 0,47123E quindi :
A= L^2 \cdot \sin \alpha = (100 \text{cm})^2 \cdot \sin (0,47123) \approx 4540 \text{cm}^2Conclusioni
Per quanto riguarda le formule per il calcolo dell’area del rombo è tutto. Precisiamo soltanto che dalle precedenti formule è possibile stabilire delle utili formule inverse. Così ad esempio se abbiamo come dati di partenza l’area {A} e la misura di una diagonale possiamo ricavare l’altra diagonale:
d_1 = \dfrac{2 \cdot A}{d_2}, \qquad d_2=\dfrac{2 \cdot A}{d_1}Inoltre, nota l’area {A} e il lato {L} possiamo ricavare l’altezza:
h=\dfrac{A}{L}O in alternativa, nota la misura dell’altezza {h} e l’area {A} possiamo ricavare la misura dei lati del rombo:
L=\dfrac{A}{h}Infine, nota l’area e la misura dei lati del rombo possiamo ricavare il raggio della circonferenza ad esso inscrivibile. E inoltre, nota l’area e il raggio della circonferenza inscrivibile possiamo determinare la misura dei lati:
r = \dfrac{A}{2L}; \qquad L=\dfrac{A}{2r}| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
