Area del cerchio

 - 

Domande e risposte

Quali sono le formule per il calcolo dell’area del cerchio? Come si calcola l’area del cerchio a partire dal raggio, dal diametro oppure dalla sua circonferenza?

L’area del cerchio è l’area della superficie del cerchio. Per il calcolo dell’area del cerchio dovremo scegliere la giusta formula da utilizzare in base ai nostri dati di partenza. Del resto, per risolvere ogni problema la prima cosa da fare è controllare i dati che abbiamo.

Ad esempio, possiamo avere come dato di partenza il raggio {r}:

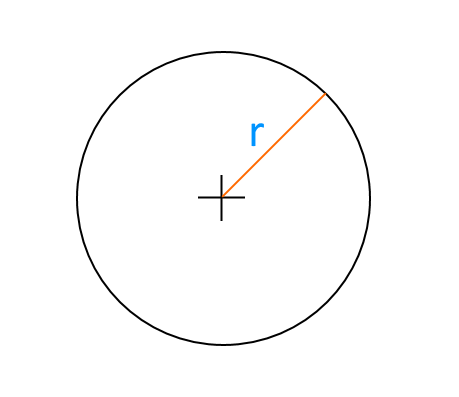
In tal caso possiamo calcolare l’area del cerchio con la formula:

A= \pi \cdot r^2

nella quale Pi Greco è un famosissimo numero fisso che generalmente può essere approssimato con {3,14} (o in modo più raffinato con {3,14159}).

In altre parole, l’area di tale figura si ottiene moltiplicando Pi Greco per il quadrato del raggio. Equivalentemente, se ci resta più facile possiamo moltiplicare il raggio per sé stesso e quindi moltiplicare il risultato ottenuto per Pi Greco:

A = r \cdot r \cdot \pi

Se il dato di partenza è invece il diametro {d}:

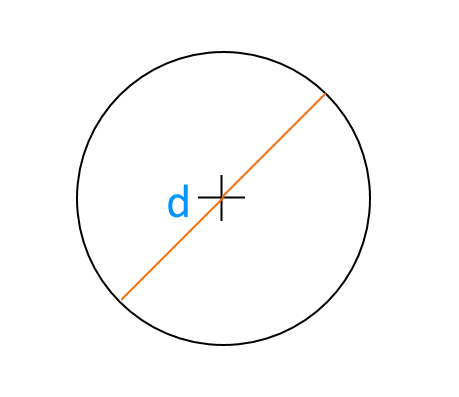
allora utilizziamo la formula:

A = \pi \cdot \dfrac{d^2}{4}

Dovremo in questo caso moltiplicare tra loro Pi Greco e la quarta parte del quadrato del diametro.

Infine, se il nostro dato di partenza è la circonferenza {C} del cerchio (ovvero la misura del perimetro del cerchio), allora utilizzeremo la formula:

A = \dfrac{C^2}{4\pi}

Passiamo subito agli esempi in modo da vedere nella pratica come utilizzare le formule che abbiamo appena illustrato.

Esempi

Esempio 1

Dato di partenza: raggio {2 \text{cm}}.

Abbiamo:

A = \pi \cdot r^2 = \pi \cdot (2  \text{cm})^2 = \pi \cdot 4 \text{cm}^2 \approx 3,14 \cdot 4 \text{cm}^2=12,56 \text{cm}^2

Esempio 2

Dato di partenza: diametro {d=12 \text{mm}}.

Abbiamo:

A = \pi \cdot \dfrac{d^2}{4}= \pi \cdot \dfrac{(12 \text{mm})^2}{4} \approx 3,14 \cdot \dfrac{144}{4} \text{mm}^2=113,04 \text{mm}^2

Esempio 3

Dato di partenza: circonferenza {C=35 \text{cm}}.

Abbiamo:

A=\dfrac{ C^2}{4 \cdot \pi}=\dfrac{(35\text{cm})^2}{4 \cdot \pi} \approx \dfrac{1225 \text{cm}^2}{4 \cdot 3,14} = 97,53 \text{cm}^2

Come ricordare la formula dell’area del cerchio nelle sue differenti versioni

Non occorre ricordare tutte e tre le formule dell’area del cerchio. L’unica formula che serve veramente ricordare è quella basata sul raggio:

A=\pi \cdot r^2

Se infatti abbiamo come dato di partenza il diametro, ci basta ricordare che per definizione {d=2 \cdot r } (il diametro è il doppio del raggio) e che quindi il raggio è la metà del diametro, ovvero {r=\dfrac{d}{2}}. Si tratterà allora di sostituire nella precedente formula ad {r} la quantità {\dfrac{d}{2}} ottenendo:

A= \pi \cdot \left( \dfrac{d}{2}\right)^2=\pi \cdot \dfrac{d^2}{4}

Ricordiamo infatti che il quadrato di una frazione è uguale al quadrato del numeratore fratto il quadrato del denominatore.

Se invece come dato di partenza abbiamo la circonferenza, basta ricordare che:

C=2 \pi r

da cui dividendo entrambi i membri dell’uguaglianza per {2 \pi} otteniamo la formula inversa:

r=\dfrac{C}{2 \cdot \pi}

A questo punto ci basta sostituire l’espressione per {r} appena ottenuta nella formula dell’area del cerchio a partire dal raggio:

A=\pi \cdot r^2 = \pi \cdot \left( \dfrac{C}{2 \cdot \pi}\right)^2 = \pi \cdot \dfrac{C^2}{(2 \cdot \pi)^2} =\pi \cdot \dfrac{C^2}{2^2 \cdot \pi^2} = \cancel{\pi} \cdot \dfrac{C^2}{4 \pi ^{\cancel{2}^{\scriptsize \displaystyle1}}}=\dfrac{C^2}{4\pi }

Per comprendere tutti i passaggi può essere utile un ripasso sulle proprietà delle potenze.

Con i trucchi qui mostrati è dunque sufficiente ricordare una sola formula per il calcolo dell’area della figura.