Proprietà delle potenze

 - 

Domande e risposte

Quali sono le proprietà delle potenze e quale è la loro utilità?

Le proprietà delle potenze consentono di eseguire più rapidamente i calcoli nei quali sono presenti delle potenze. Le proprietà delle potenze più importanti sono le regole del prodotto e del rapporto tra potenze di uguale base, le regole del prodotto tra potenze di uguale esponente, ed infine la regola delle potenze di potenze.

Supponiamo ad esempio di dover calcolare il prodotto:

2^3 \cdot 2^5

Piuttosto che calcolare le potenze {2^3} e {2^5} possiamo sfruttare la proprietà del prodotto tra potenze di uguale base: il prodotto tra potenze di uguale base è uguale ad una potenza che ha per base la stessa base e per esponente la somma degli esponenti.

Così nel nostro caso possiamo scrivere direttamente:

2^3 \cdot 2^5 =2^{3+5}=2^8=256

Infatti, {2^3 = 8} e {2^5=32} e quindi:

2^3 \cdot 2^5 = 8 \cdot 32 =256

Così grazie alle proprietà delle potenze siamo riusciti a calcolare il prodotto di partenza senza dover calcolare le singole potenze relative ai fattori nel prodotto. Ovviamente il vantaggio diventa più evidente al crescere del numero dei fattori in gioco. Ad esempio:

2^2 \cdot 2^3 \cdot 2^4 = 2^{2+3+4}=2^{9}=512

Il calcolo è sicuramente molto più pratico rispetto a dover calcolare tutte le potenze relativamente a ciascun fattore e moltiplicarle tra loro:

2^2 \cdot 2^3 \cdot 2^4 =4 \cdot 8 \cdot 16 = 32 \cdot 16 = 512

A seguire riportiamo una tabella che riassume tutte le proprietà delle potenze.

Tabella delle proprietà delle potenze

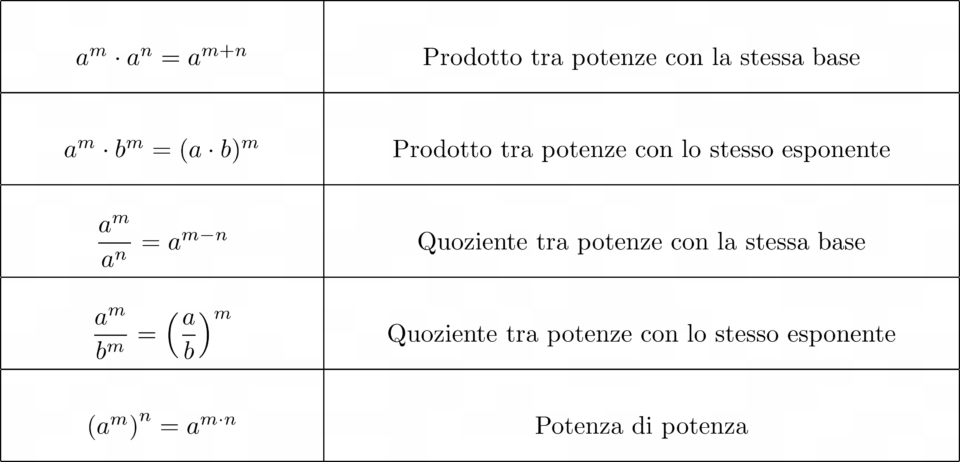
Vediamo ora un po’ più nel dettaglio ciascuna proprietà fornendo degli esempi di utilizzo.

Prodotto tra potenze con la stessa base

Il prodotto tra potenze con la stessa base è uguale ad una potenza avente per base la stessa base e per esponente la somma degli esponenti delle potenze nel prodotto. {a^m \cdot a^n = a^{m+n}}

La proprietà consente come abbiamo visto nell’introduzione di moltiplicare potenze numeriche tra loro senza dover calcolare le singole potenze presenti nel prodotto.

Inoltre, la proprietà del prodotto tra potenze con la stessa base interviene nel prodotto tra monomi (e quindi anche nel prodotto tra polinomi). Ad esempio:

ab \cdot a^2b^3=a^3b^4

Il risultato si può dimostrare agevolmente utilizzando le proprietà delle potenze. Riordinando i fattori nel prodotto abbiamo infatti:

a \cdot a^2 \cdot b \cdot b^3 =a^1 \cdot a^2\cdot b^1 \cdot b^3=a^{1+2}\cdot b^{1+3}=a^3 b^{4}

Come è possibile notare abbiamo riordinato i fattori in modo da individuare dei prodotti tra potenze aventi la stessa base, rispettivamente un prodotto con potenze aventi base {a}, e un prodotto con potenze aventi basi {b}.

Vediamo un ultimo esempio:

(a+b)^2 \cdot (a+b)=(a+b)^2 \cdot (a+b)^1 = (a+b)^{2+1}=(a+b)^3

In questo modo è possibile calcolare rapidamente il risultato del prodotto esprimendolo come una potenza. Diversamente avremmo dovuto calcolare il quadrato del binomio e quindi eseguire il prodotto tra polinomi:

\begin{align*} & (a+b)^2 \cdot (a+b) = (a^2+2ab+b^2) (a+b) = \\ \\ & =a^3+2a^2b+ab^2+a^2b+2ab^2+b^3=a^3+3a^2b+3ab^2+b^3=\\ \\ & =(a+b)^3 \end{align*}

E’ dunque evidente la praticità delle proprietà delle potenze.

Osserviamo che è possibile utilizzare la proprietà anche in senso inverso. Ad esempio:

(a+b+c)^3 = (a+b+c)^2 \cdot (a+b+c)

E’ infatti possibile vedere l’esponente {3} come somma degli esponenti {2} e {1} relativi a potenze aventi la stessa base moltiplicate tra loro.

Ciò consente ad esempio di ricondurre il calcolo del cubo di un trinomio al prodotto del quadrato del trinomio per il trinomio stesso.

Prodotto tra potenze con lo stesso esponente

Un’altra proprietà delle potenze molto ricorrente nel calcolo letterale è il prodotto tra potenze con lo stesso esponente.

Il prodotto tra potenze con lo stesso esponente è uguale ad una potenza che ha per esponente lo stesso esponente e per base il prodotto delle basi. {a^m \cdot b^m = (a \cdot b) ^ m}

Ad esempio:

2^3 \cdot 3^3 =  (2 \cdot 3)^3 = 6^3 = 36 \cdot 6 = 216

Diversamente, calcolando le singole potenze nel prodotto:

2^3 \cdot 3^3 = 8 \cdot 27 = 216

La proprietà è molto usata anche nel calcolo letterale. Ad esempio:

a^2 \cdot b^2 = (ab)^2

Osserviamo che è possibile utilizzare la proprietà anche in senso inverso:

(ab)^2=a^2b^2

Dunque la potenza di un prodotto è uguale al prodotto delle potenze dei singoli fattori.

Quoziente tra potenze di uguale base

Veniamo ora ad un’altra importante proprietà delle potenze.

Il quoziente tra potenze di uguale base è uguale ad una potenza avente per base la stessa base e per esponente la differenza tra l’esponente della potenza al dividendo e l’esponente della potenza al divisore. {\dfrac{a^m}{a^n} = a^{m-n}}

Ad esempio:

2^3:2^2=2^{3-2}=2^1=2

Ciò ci ha risparmiato di dover calcolare le singole potenze e quindi eseguire la divisione:

2^3:2^2=8:4=2

La proprietà interviene ovviamente nella divisione tra monomi:

a^2b:(ab) = a

Infatti:

a^2b:(ab)= (a^2:a^1)\cdot(b^1:b^1)=a^{2-1}\cdot b^0 = a^1 \cdot 1 = a

Come ulteriore esempio:

(a+b)^3:(a+b)^2=(a+b)^{3-2}=(a+b)^1=a+b

Grazie alle proprietà delle potenze ci risparmiamo in questo caso la fatica di dover calcolare le singole potenze ed eseguire la divisione tra i corrispondenti polinomi:

\begin{align*} & (a+b)^3=a^3+3a^2b+3ab^2+b^3; \quad (a+b)^2=a^2+2ab+b^2  \\ \\ & (a^3+3a^2b+3ab^2+b^3):(a^2+2ab+b^2)=a+b\end{align*}

Quoziente tra potenze con lo stesso esponente

Il quoziente tra potenze con lo stesso esponente è uguale ad una potenza che ha per esponente lo stesso esponente e per base il quoziente tra le basi.{\dfrac{a^m}{b^m} = \left(\dfrac{a}{b}\right) ^ m}

Così ad esempio:

10^5:5^5=(10:5)^5=2^5=32

E’ evidente la maggior praticità del calcolo rispetto a dover calcolare le singole potenze dividendo poi i risultati tra loro:

10^5:5^5=100000:3125=32

La proprietà è di uso ricorrente anche nel calcolo letterale. Ad esempio:

\dfrac{a^3}{b^3}=\left( \dfrac{a}{b}\right)^3

Utilizzando la proprietà in senso inverso è inoltre possibile calcolare la potenza di una frazione:

\left( \dfrac{a}{b}\right)^3=\dfrac{a^3}{b^3}; \qquad \left( \dfrac{3}{4}\right)^2=\dfrac{3^2}{4^2}=\dfrac{9}{16}

Proprietà della potenza di una potenza

Un’ultima importantissima proprietà delle potenze è la regola della potenza di una potenza.

La potenza di una potenza è uguale ad una potenza avente per base la stessa base e per esponente il prodotto tra gli esponenti. {\left(a^m\right)^n = a^{m \cdot n}}

Così ad esempio:

\left( 3^3\right)^2= 3^{3 \cdot 2}=3^6=729

Diversamente avremmo dovuto calcolare la potenza più interna e quindi elevare il risultato al quadrato:

\left( 3^3\right)^2=(27)^2=729

La proprietà della potenza di una potenza presenta una moltitudine di applicazioni nel calcolo letterale ed algebrico in genere. Consideriamo ad esempio la seguente equazione:

x^4-5x^2+4=0

Si tratta di un’equazione di quarto grado, per la quale non è certo di comune uso la formula risolutiva. Tuttavia, sfruttando la proprietà della potenza di una potenza nel termine {x^4} possiamo riscrivere l’equazione come:

(x^2)^2-5x^2+4=0

A questo punto basta sostituire ad {x^2} la variabile {t}:

t^2-5t+4=0

Ora ci ritroviamo con un’equazione di secondo grado, che è possibile risolvere con tecniche standard. Poi con opportuni ragionamenti sarà possibile ricavare le soluzioni nella variabile {x}.

Sulla proprietà della potenza di potenza si basano quindi numerose tecniche risolutive di vari problemi che richiedono delle sostituzioni del tipo che abbiamo appena visto.

Dimostrazioni intuitive delle proprietà delle potenze

Cerchiamo a questo punto di capire la logica che sta dietro alle proprietà delle potenze. In questo modo ci sarà più semplice ricordarle ed eviteremo ancor meglio possibili errori.

Proprietà del prodotto tra potenze di uguale base

Consideriamo ad esempio il seguente prodotto:

a^2 \cdot a^3=a^{2+3} = a^5

Perché dobbiamo considerare la somma degli esponenti? Osserviamo che il prodotto può essere riscritto come:

\overbrace{a \cdot a}^{a^2} \cdot \overbrace{a\cdot a \cdot a}^{a^3}=\overbrace{a \cdot a \cdot a \cdot a \cdot a}^{a^5}

Come possiamo vedere eseguendo la moltiplicazione quello che facciamo è aggiungere dei fattori {a}.

Nel prodotto tra potenze di uguale base interviene la somma degli esponenti e non il prodotto.

Proprietà del prodotto tra potenze di uguale esponente

Vogliamo far vedere perché ad esempio si ha:

a^3 \cdot b^3 = (a \cdot b)^3

Osserviamo che per la definizione di potenza possiamo scrivere:

\boxed{(a \cdot b) ^3} =  (a\cdot b) \cdot (a\cdot b) \cdot (a\cdot b) =

Riordinando i fattori:

= a \cdot a \cdot a \cdot b \cdot b \cdot b = \boxed{a^3 \cdot b^3}

Proprietà del quoziente tra potenze di uguale base e quoziente tra potenze di uguale esponente

Queste proprietà si dimostrano in modo delle tutto simile alle precedenti.

Per la proprietà del quoziente tra potenze di uguale base abbiamo ad esempio:

a^3:a^2=a^{3-2}=a^1=a

Infatti:

a^3:a^2=\dfrac{\cancel{a} \cdot \cancel{a} \cdot a}{\cancel{a} \cdot \cancel{a}}=a

Così eseguendo la divisione in pratica togliamo dei fattori.

Nel quoziente tra potenze di uguale base interviene la differenza tra gli esponenti e non il rapporto.

Per la proprietà del quoziente tra potenze di uguale esponente abbiamo ad esempio:

\dfrac{a^3}{b^3}=\left( \dfrac{a}{b}\right)^3

Infatti:

\dfrac{a^3}{b^3}=\dfrac{a \cdot a \cdot a}{b \cdot b \cdot b}=\dfrac{a}{b} \cdot \dfrac{a}{b} \cdot \dfrac{a}{b}=\left( \dfrac{a}{b}\right)^3

Proprietà della potenza di potenza

Vediamo infine di giustificare intuitivamente la proprietà della potenza di potenza. Proviamo a capire perché ad esempio:

(a^3)^2 = a^{3 \cdot 2} = a^6

Osserviamo che per la definizione di potenza e la proprietà del prodotto tra potenze di uguale base abbiamo:

\boxed{(a^3)^2} = a^3 \cdot a^3 = a^{3+3} = a^6=\boxed{a^{3 \cdot 2}}

Nella proprietà della potenza di una potenza interviene il prodotto tra gli esponenti.

Conclusioni sulle proprietà delle potenze

Per quanto riguarda le proprietà delle potenze è tutto. Abbiamo qui ricordato le regole dandone una giustificazione intuitiva ed evidenziando gli errori da evitare. E’ importante avere un’ottima dimestichezza con queste proprietà poiché intervengono praticamente ovunque in algebra ed analisi. Un altro esempio di uso delle proprietà delle potenze di potenze è dato ad esempio dai calcoli con quantità espresse in notazione scientifica.

Buono studio a tutti voi!