Come si procede per calcolare la media ponderata (media pesata)? Quale è la differenza rispetto alla media aritmetica?
La media ponderata si distingue dalla media aritmetica per il fatto che oltre alle quantità delle quali dobbiamo calcolare la media abbiamo anche i rispettivi pesi.
Così per calcolare la media ponderata tra certi numeri dovremo anche conoscere il peso attribuito a ciascun numero. Il termine “ponderata” derivata dal latino “pondus” che significa peso. Un sinonimo di media ponderata è infatti media pesata.
Supponiamo di dover calcolare la media aritmetica dei seguenti numeri:
1, \quad 5, \quad 20
Si tratterà in questo caso di sommare i numeri tra loro e dividere il risultato per {3}, ovvero per la quantità dei numeri presenti:
M=\dfrac{1+5+20}{3}=\dfrac{26}{3} \approx 8,66Per il calcolo della media ponderata (o media pesata) dobbiamo disporre come dati di partenza anche dei pesi attribuiti a ciascun numero. Supponiamo ad esempio che il peso attribuito al numero {1} sia {60}, il peso attribuito al numero {5} sia {10} e il peso attribuito al numero {20} sia {30}.
Per il calcolo della media pesata dovremo dividere tra loro la somma di tutti i prodotti di ciascun numero per il rispettivo peso e la somma dei pesi.
Indicando così con {n_1, \: n_2, \: n_3} i numeri dei quali calcolare la media ponderata e {p_1, \: p_2, \: p_3 } i rispettivi pesi nel nostro caso abbiamo:
M_p=\dfrac{n_1 \cdot p_1 + n_2 \cdot p_2 + n_3 \cdot p_3}{p_1+p_2+p_3}E quindi, sostituendo i valori numerici:
\begin{align*} & M_{p} = \dfrac{1 \cdot 60+5 \cdot 10+ 20 \cdot 30}{60+10+30}=\dfrac{60+50+600}{100}=\\ \\ & =\dfrac{\cancel{10}(6+5+60)}{10\cancel{0}} = \dfrac{71}{10}=7,1\end{align*}Osserviamo che in questo caso la media pesata ha un valore minore rispetto alla media aritmetica calcolata in precedenza. Ciò non è una coincidenza. Infatti, abbiamo attribuito il peso più grande al numero più piccolo.
Dunque in termini pratici la media pesata consente di calcolare la media tra determinate quantità dando a ciascuna l’opportuna importanza. Invece la media aritmetica tratta tutte le quantità allo stesso modo.
In generale indicati con {n_1, \: n_2, \: \dots, n_k} i numeri dei quali calcolare la media pesata e {p_1, \: p_2, \: , \dots , p_n} i rispettivi pesi abbiamo la seguente formula per il calcolo della media pesata:
M_p = \dfrac{n_1 \cdot p_1 + n_2 \cdot p_2+ \dots + n_k \cdot p_k }{p_1+p_2 + \dots +p_k}, \qquad k \in \mathbb{N}la quale può essere scritta in forma più compatta utilizzando le sommatorie:
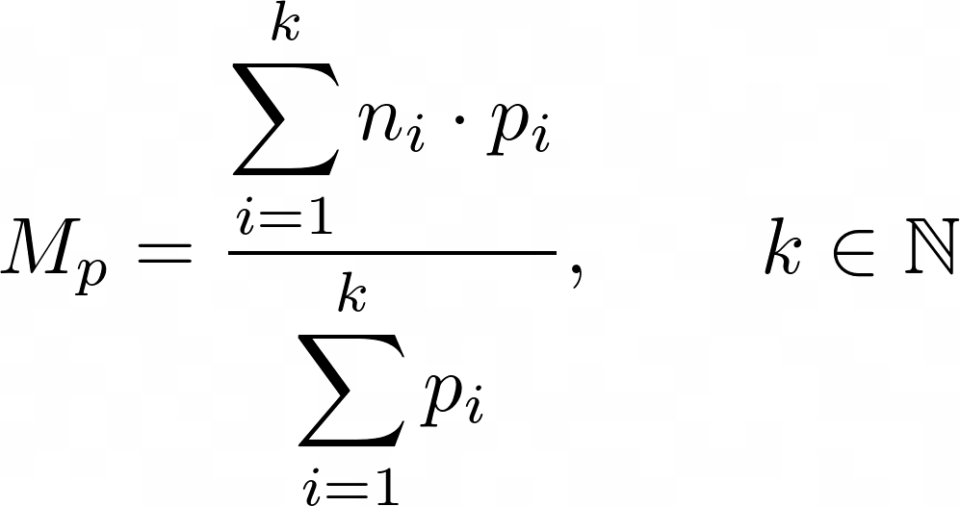
Osserviamo che la media aritmetica non è altro che un caso particolare della media pesata ove i pesi sono tutti uguali a {1}. Infatti, ponendo {p_1=p_2= \dots = p_k = 1}, la precedente formula si riduce a:
M=\dfrac{\displaystyle \sum _{i=1}^{k}n_i \cdot 1}{\displaystyle {\sum _{i=1}^{k}1}}=\dfrac{n_1+n_2+\dots +n_k}{k}infatti {\displaystyle \sum_{i=1}^{k}1 = k \cdot 1 = k}.
Un problema con la media ponderata
Calcolare il peso (massa) di un solido formato da più materiali uniti insieme, avente volume {V} di {37 \text{cm}^3}, sapendo che è costituito per il {30 \%} da rame, per il {60 \%} da alluminio e per il restante {10 \%} da bronzo.
Si assumano per le masse volumiche dei materiali indicati i seguenti valori:
p_{s, \text{rame}}=9 \text{g}/\text{cm}^3, \qquad p_{s, \text{alluminio}}=2,7 \text{g}/\text{cm}^3, \qquad p_{s, \text{bronzo}}=8 g/ \text{cm}^3Per risolvere il problema, l’idea è quella di moltiplicare il volume del solido per la media ponderata delle masse volumiche di ciascun metallo.
Di conseguenza, le percentuali di ciascun metallo andranno considerate come il peso da attribuire a ciascun valore della massa volumica. Così, indicando la media ponderata delle masse volumiche con {p_{s, M}} abbiamo:
p_{s, M}=\dfrac{30 \cdot 9 +60 \cdot 2,7+10 \cdot 8}{30+60+10}=\dfrac{270+162+80}{100}=5,12 \text{g} / \text{cm}^3Infine per il peso {P} (massa) del solido:
P= V \cdot p_{s, M} = 37 \text{cm}^3 \cdot 5,12 \dfrac{\text{g}}{\text{cm}^3}=189,44 \text{g}Osserviamo che la grande percentuale di alluminio nonostante la presenza di bronzo e rame rende il peso (massa) del solido minore di quanto ci saremmo potuti aspettare. Infatti considerando (erroneamente) la media aritmetica delle masse volumiche:
p'=\dfrac{(9+2,7+8) \text{g} / \text{cm}^3}{3} \approx 6,57 \text{g}/ \text{cm}^3da cui segue un peso (massa) per il solido pari a:
P=V \cdot p' = 37 \cdot 6,57=243,09 \text{g}/ \text{cm}^3Il valore della media ponderata è inferiore poiché tiene invece conto dei pesi attribuiti a tutti i valori dei quali calcolare la media.
Osserviamo infine che avremmo potuto risolvere il problema anche senza utilizzare (esplicitamente) la formula della media pesata. Infatti, possiamo suddividere il volume totale nei volumi corrispondenti a ciascun metallo. Tenendo conto allora di ciascuna percentuale, cominciamo calcolando il volume della parte di solido fatta di rame:
V_{\text{rame}}=\dfrac{30}{100} \cdot V=\dfrac{30}{100} \cdot 37 =11,1 \text{cm}^3e allo stesso modo, per l’alluminio:
V_\text{alluminio}=\dfrac{60}{100} \cdot 37 = 22,2 \text{cm}^3e infine per il bronzo:
V_{\text{bronzo}}=\dfrac{10}{100} \cdot 37=3,7 \text{cm}^3E quindi per il peso (massa) del solido avremo:
\begin{align*} & P=V_{\text{rame}} \cdot p_{s, \text{rame}} + V_{\text{alluminio}} \cdot p_{s, \text{allumino}} + V_{\text{bronzo}} \cdot p_{s, \text{bronzo}} = \\ \\ & =11,1 \cdot 9 + 22,2 \cdot 2,7+3,7 \cdot 8 = 189,44 \text{g} \end{align*}Ciò dimostra la correttezza dei ragionamenti fatti per l’utilizzo della media ponderata.
Come ultima nota, precisiamo che la somma dei pesi non deve essere necessariamente {100}. Tuttavia, negli esempi abbiamo utilizzato le percentuali perché probabilmente è quello che più rende l’idea del significato della media ponderata.
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
