Coordinate cartesiane nel piano

 - 

Coordinate cartesiane e retta nel piano

Le coordinate cartesiane nel piano consentono di individuare un qualunque punto nel piano cartesiano mediante due valori numerici, detti rispettivamente ascissa e ordinata, relativi a due rette orientate indicate con i nomi di asse x e asse y.

Introducendo le coordinate cartesiane nel piano passiamo così da un sistema di riferimento dato da una sola retta r (vedi lezioni precedenti) ad un sistema di riferimento costituito invece da due rette, solitamente ortogonali tra loro.

Di conseguenza, utilizzando questo nuovo sistema di riferimento potremo individuare punti qualsiasi nel piano cartesiano, a patto di conoscere le loro coordinate relative ad entrambi gli assi {x} e {y}. Sarà quindi possibile rappresentare punti, semirette, rette, segmenti, curve, domini piani e figure piane in generale.

Diversamente, nel caso del sistema di riferimento dato da una sola retta {r}, non potevamo che rappresentare punti, segmenti e semirette. Di qui la grande utilità dell’uso delle coordinate cartesiane nel piano.

Coordinate cartesiane nel piano: sistema di riferimento cartesiano ortogonale costituito da due assi

Consideriamo due rette ciascuna dotata di un suo proprio sistema di riferimento. Le rette giacciono entrambe in uno stesso piano detto piano cartesiano. Tale piano è uno spazio di due dimensioni nel quale vivono gli enti geometrici che via via considereremo (punti, segmenti, rette, semirette, curve, domini piani, figure piane).

Chiamiamo le due rette rispettivamente asse x (o asse delle ascisse) e asse y (o asse delle ordinate). Le due rette sono ortogonali tra loro ed hanno come punto di intersezione il punto {O} detto origine degli assi, o semplicemente origine.

In questo modo, sarà possibile individuare un qualsiasi punto del piano cartesiano mediante due valori numerici: la coordinata sull’asse {x} (detta ascissa) e la coordinata sull’asse {y} (detta ordinata).

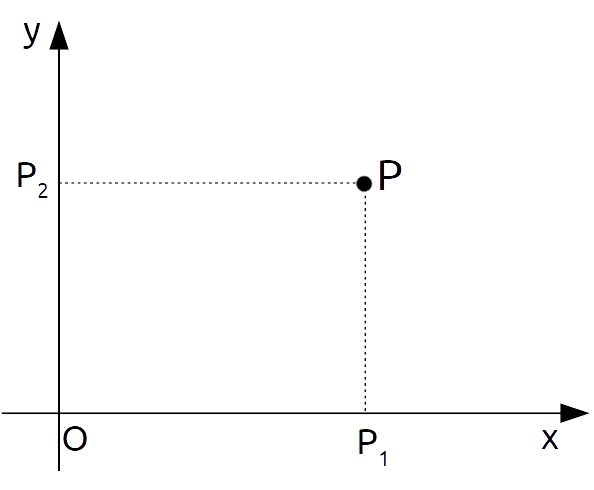
Così facendo otteniamo una corrispondenza biunivoca tra i punti del piano e le coppie ordinate {(x,y)}, con {x, \: y} valori reali.

Così ad esempio per il punto {P} in figura abbiamo:

P=(P_1, P_2)

ove {P_1} è un numero reale che rappresenta l’ascissa del punto {P}, mentre {P_2} è un numero reale che rappresenta l’ordinata del punto {P} stesso. In altre parole, {P_1} è la coordinata del punto {P} lungo l’asse {x}, mentre {P_2} è la coordinata del punto {P} lungo l’asse {y}.

Ora, le coppie del tipo {(x,y)} sono ordinate poiché in esse è importante l’ordine con il quale si presentano le coordinate {x} e {y}. Infatti in generale abbiamo:

(x,y) \neq (y,x)

Così ad esempio la coppia ordinata {(5,2)} individua nel piano cartesiano un differente punto rispetto alla coppia {(2,5)}.

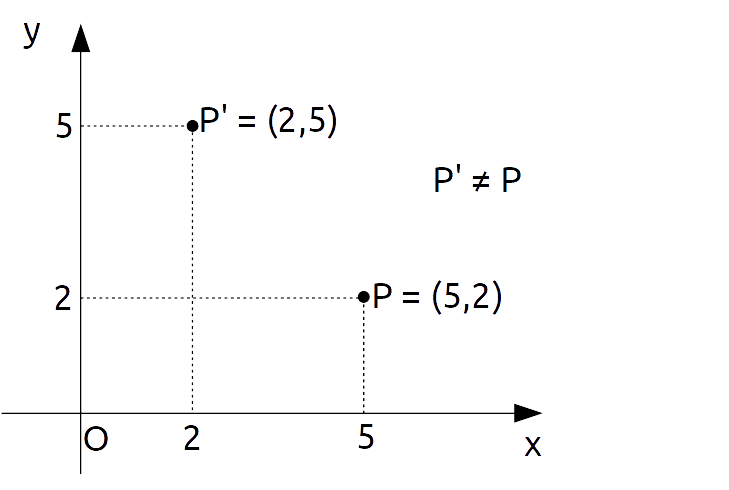
Ora, in generale l’unità di misura fissata per l’asse {x} può essere differente da quella fissata per l’asse {y}. In particolare, se tali unità di misura sono differenti abbiamo un sistema di coordinate cartesiane dimetrico. Se invece viene fissata per entrambi gli assi una stessa unità di misura, allora il sistema di riferimento così stabilito si dice monometrico. Nel corso di queste lezioni ci riferiremo sempre a sistemi di riferimento del tipo monometrico. Così, in parole povere, nel vostro quaderno potrete considerare come unità di misura per entrambi gli assi un “quadretto”.

Quadranti e loro classificazione in base al segno delle coordinate cartesiane nel piano relative ai punti ad essi appartenenti

I due assi {x} e {y} dividono il piano cartesiano in quattro parti dette quadranti.

Il primo quadrante è quello i cui punti hanno entrambe le coordinate positive. Nel secondo quadrante invece abbiamo punti con ascissa negativa ed ordinata positiva. Nel terzo quadrante l’ascissa e l’ordinata dei suoi punti sono invece entrambe negative. Infine, nel quarto quadrante abbiamo punti con ascissa positiva ed ordinata negativa.

Alcune proprietà

L’origine {O} è l’unico punto del piano cartesiano tale da avere entrambe le coordinate {x} e {y} nulle:

O=(0,0)

In altre parole, l’origine è un punto avente ascissa ed ordinata entrambe uguali a zero.

Ora, è importante notare che tutti i punti dell’asse {x} sono tali da avere ordinata nulla. In altre parole, ogni punto appartenente all’asse {x} è del tipo:

P=(x,0) \qquad \text{punti dell'asse } x 

Viceversa, tutti i punti dell’asse {y} sono tali da avere ascissa nulla:

P'=(0,y) \qquad \text{punti dell'asse } y

Così, tutti i punti dell’asse {x} sono tali da rispettare l’equazione:

y=0, \qquad \text{asse }x

mentre tutti i punti dell’asse {y} sono tali da rispettare l’equazione:

x=0, \qquad \text{asse }y

Così, sostituendo le coordinate di ciascun punto appartenente all’asse {x} o all’asse {y} nella relativa equazione, quest’ultima risulta verificata.

Osserviamo ora che gli assi {x} e {y} non sono che delle particolari rette. E ad esempio, se l’asse {x} è rappresentato dall’equazione:

y=0

allora una qualunque retta parallela all’asse {x} avrà equazione:

y=k, \qquad k \in \R

Osserviamo che tutti i punti appartenenti ad una parallela all’asse {x} hanno la stessa ordinata. Ciò vale, evidentemente, anche per tutti i punti appartenenti all’asse {x} stesso, i quali effettivamente hanno tutti ordinata nulla.

Infine, tutti i punti appartenenti all’asse {y} o ad una retta parallela all’asse {y} hanno la stessa ascissa.

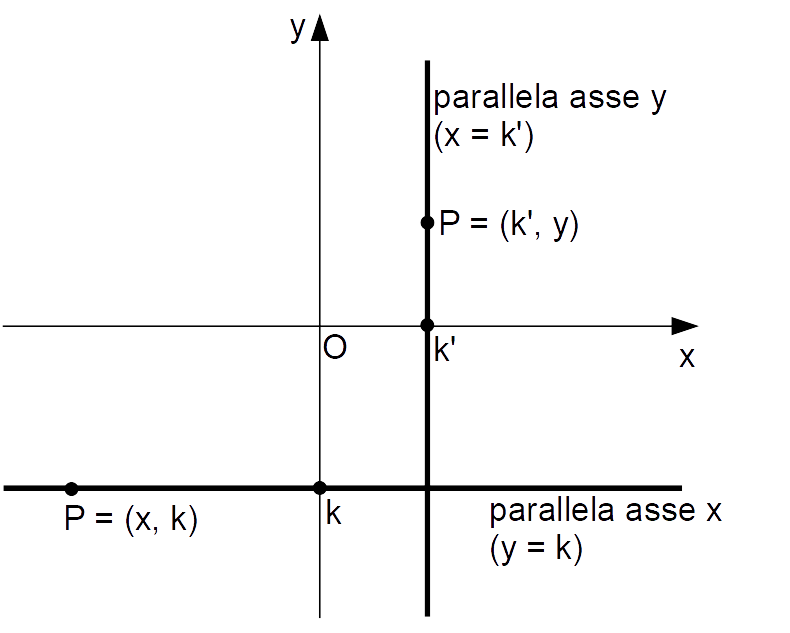
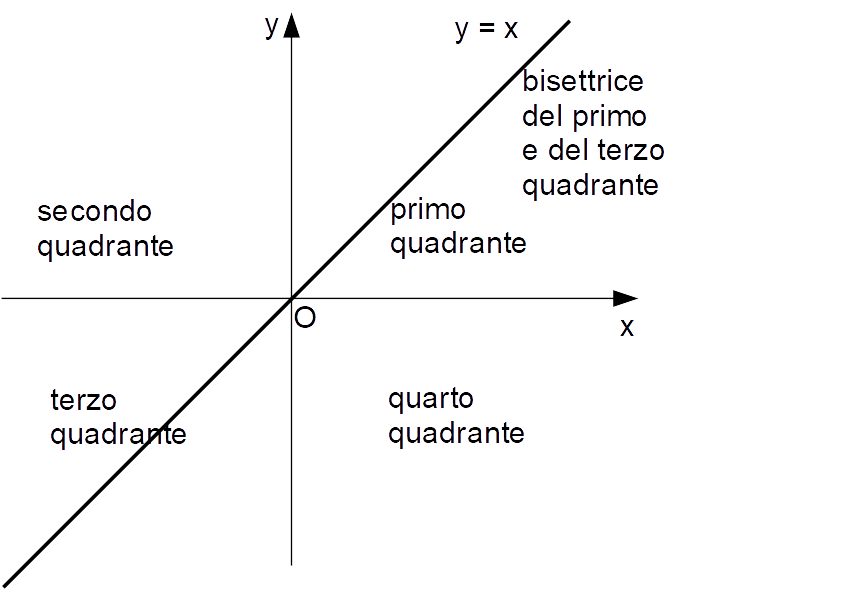
Bisettrice del primo e terzo quadrante e bisettrice del secondo e quarto quadrante

A conclusione della lezione consideriamo delle particolari rette indicate con il termine di bisettrici.

In particolare, tutti i punti del tipo:

(a,a), \qquad \forall  \: a \in \R

soddisfano l’equazione:

y=x

ed appartengono alla retta bisettrice del primo e terzo quadrante:

Infine, tutti i punti del tipo:

(a,-a), \qquad a \in \R

soddisfano l’equazione:

y=-x

ed appartengono alla bisettrice del secondo e quarto quadrante:

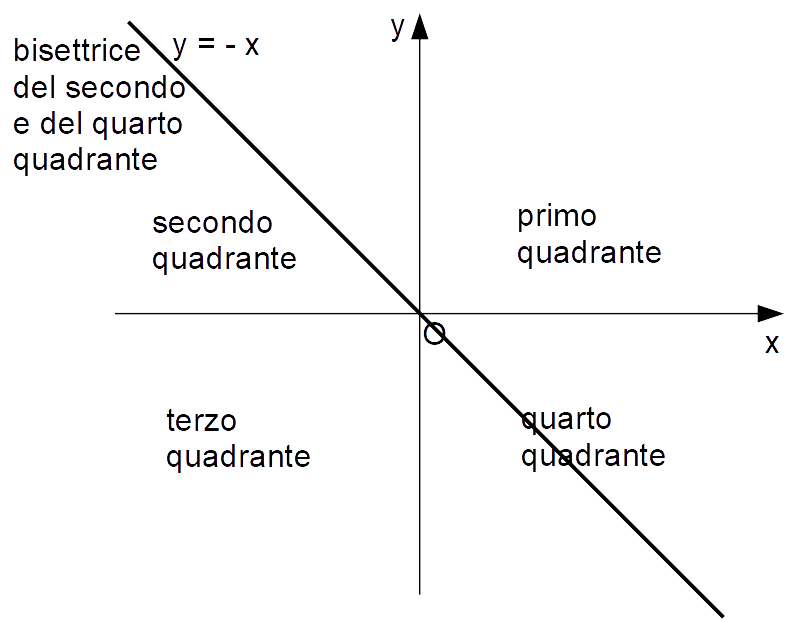
Osserviamo che il termine “bisettrice” si riferisce ad una retta che divide il piano cartesiano in due parti (bisettrice = che divide in due settori o parti). Ed effettivamente entrambe le bisettrici su indicate dividono il piano cartesiano in due parti (più propriamente in due semipiani).

Distanza di un punto dagli assi cartesiani

Consideriamo un punto {P=(x,y)} sul piano cartesiano. La retta parallela all’asse {x} passante per il punto {P} si interseca con l’asse {y} nel punto {P_2=(0, y)}. Allo stesso modo, la retta parallela all’asse {y} passante per il punto {P} si interseca con l’asse {x} nel punto {P_1 = (x,0)}. Indichiamo tali rette rispettivamente con {r_x} e {r_y}, ove il pedice corrisponde all’asse rispetto al quale la retta è parallela (vedi figura a seguire).

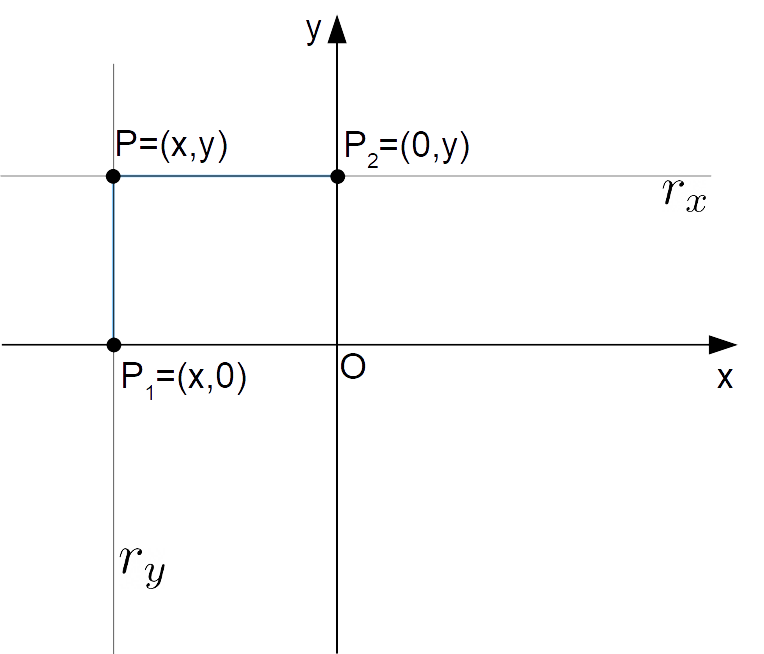
Ora, nella precedente lezione abbiamo visto la nozione di distanza tra due punti su una retta {r}. Sfruttando proprio tale nozione possiamo definire la distanza di un punto {P} del piano cartesiano rispetto agli assi {x} e {y}. In particolare:

• la distanza di un punto {P} rispetto all’asse {y}, che indichiamo con {\overline{PP_2}}, è data dalla distanza sulla retta {r_x} tra il punto {P} e il punto {P_2};
• la distanza di un punto {P} rispetto all’asse {x}, che indichiamo con {\overline{PP_1}}, è data dalla distanza sulla retta {r_y} tra il punto {P} e il punto {P_1}.

Quindi abbiamo, rispettivamente:

\begin{align*} &\overline{PP_2} = |x|, \qquad \text{distanza di P dall'asse y} \\ \\ &  \overline{PP_1} = |y|, \qquad \text{distanza di P dall'asse x} \end{align*}

Così ad esempio il punto {P=(-5,7)} ha una distanza rispetto all’asse {x} uguale a {|7|}, ovvero {7}, e una distanza rispetto all’asse {y} uguale a {|-5|}, ovvero {5}.

Per quanto riguarda questa lezione relativa alle coordinate cartesiane nel piano è tutto. Nella prossima lezione introdurremo la definizione di distanza tra due punti nel piano. Buon proseguimento a tutti voi! 🙂