La distanza tra due punti nel piano si esprime come la radice quadrata della somma tra due quantità, ciascuna data dal quadrato della differenza tra le coordinate dei due punti lungo un dato asse del sistema di riferimento.
Abbiamo così anticipato la definizione di distanza tra due punti nel piano, definizione che comunque introdurremo in modo graduale e con più dettaglio nel corso di questa lezione. Tra l’altro, ci siamo già occupati del concetto di distanza tra due punti, relativamente tuttavia al solo caso della retta (vedi: distanza tra due punti sulla retta). Ora il nostro obiettivo è invece quello di calcolare la distanza tra due punti qualsiasi del piano cartesiano. E per fare questo, basterà sfruttare opportunamente la definizione di distanza tra due punti sulla retta, come mostreremo tra un istante.
Vediamo allora subito la definizione di distanza tra due punti nel piano cartesiano, proponendo i relativi esempi.
Definizione di distanza tra due punti nel piano cartesiano
Passiamo dal semplice caso del calcolo della distanza tra due punti lungo una data retta al caso più generale della distanza tra due punti del piano cartesiano.
Ricordiamo che data una retta {r}, la distanza tra due punti {A} e {B} appartenenti alla stessa retta {r} si esprime come:
D(A,B)=\overline{AB}=|b-a|ove {a} e {b} sono rispettivamente le ascisse dei punti {A} e {B} sul riferimento cartesiano dato dalla retta {r}.
Ora, consideriamo un sistema di riferimento non più costituito da una sola retta {r} ma da due assi cartesiani {x} e {y}, che si incontrano nel punto {O} detto origine degli assi (vedi: coordinate cartesiane nel piano). Su questo sistema di riferimento, consideriamo due punti {P_1} e {P_2} del piano cartesiano:
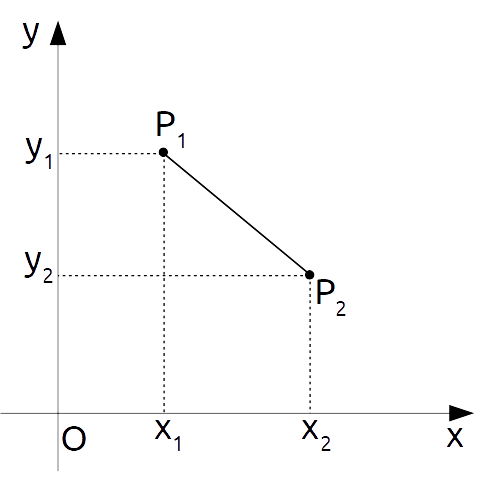
I punti {P_1} e {P_2} hanno rispettivamente ascisse date da {x_1} e {x_2} ed ordinate date da {y_1} ed {y_2}. In simboli:
P_1=(x_1, y_1), \qquad P_2=(x_2, y_2)
Ora, consideriamo la retta {r_1} passante per {P_1} e parallela all’asse {y}, e la retta {r_2} passante per {P_2} e parallela all’asse {x}. Indichiamo inoltre con {Q} il punto di intersezione tra le due rette:
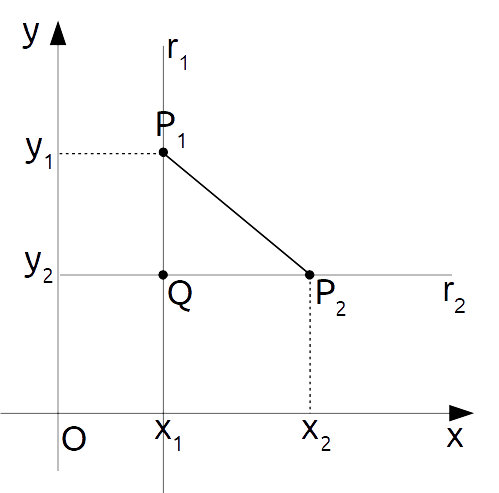
Sfruttando quanto sappiamo sulla distanza tra due punti su una retta, la distanza tra i due punti {P_1} e {Q} sulla retta {r_1} è data da:
|P_1Q|=|y_2-y_1|
Allo stesso modo, la distanza tra i punti {P_2} e {Q} sulla retta {r_2} è data da:
|P_2Q|=|x_1-x_2|
ovvero, tenendo conto della definizione di valore assoluto:
|P_2Q|=|x_2-x_1|
Il problema è ora calcolare la distanza tra i punti {P_1} e {P_2}, misurata lungo la retta che congiunge i due punti stessi. Ed è proprio questa, per definizione, la distanza tra i due punti dati nel piano cartesiano.
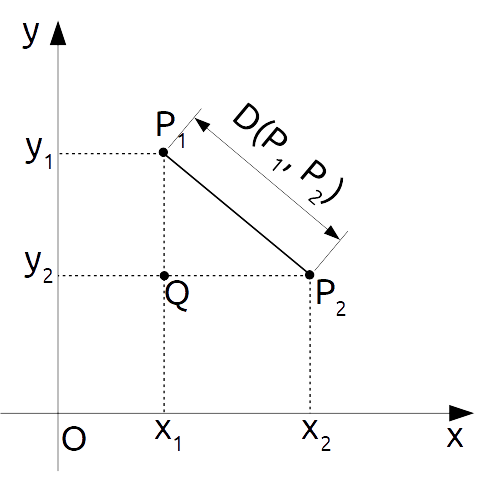
Ma niente panico: per risolvere tale problema ci viene in aiuto il teorema di Pitagora.
Consideriamo il triangolo rettangolo {\stackrel{\triangle}{P_1QP_2}}. La distanza che stiamo ricercando è data dalla misura della sua ipotenusa, ovvero:
|P_1P_2|=\sqrt{|P_1Q|^2+|P_2Q|^2}E quindi, esprimendo le misure di ciascun cateto in funzione delle coordinate cartesiane relative agli assi {x} e {y}:
|P_1P_2|=\sqrt{|y_2-y_1|^2+|x_2-x_1|^2}Inoltre, riordinando i termini all’interno del simbolo di radice possiamo scrivere:
|P_1P_2|=\sqrt{|x_2-x_1|^2+|y_2-y_1|^2}A questo punto è importante osservare che una quantità elevata al quadrato è sempre positiva. Di conseguenza, possiamo tranquillamente eliminare i simboli di valore assoluto, scrivendo in conclusione:
\boxed{ \begin{align*}\\ D(P_1, P_2)=|P_1P_2|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\ \\ \end{align*} }Abbiamo così già effettuato la dimostrazione della distanza tra due punti nel piano cartesiano, e possiamo introdurre la corrispondente definizione.
La distanza tra due punti nel piano cartesiano è data dalla radice quadrata della somma dei quadrati delle differenze delle coordinate dei due punti relative agli assi rispettivamente {x} e {y}.
Osservazioni sulla formula relativa alla distanza tra due punti nel piano cartesiano
Osserviamo anzitutto che la formula relativa alla distanza tra due punti nel piano cartesiano è ben posta, ovvero ha significato per una qualunque coppia di punti del piano cartesiano. In altre parole, il radicale che rappresenta l’espressione contenuta nella formula esiste per ogni coppia di punti {P_1} e {P_2}.
Per convincersi di questo, basta osservare che un quadrato è una quantità sempre positiva, e che la somma (intensa non in senso algebrico) di due quantità positive è a sua volta una quantità positiva. In altri termini, se eseguiamo l’operazione di addizione tra due quantità entrambe positive, il risultato sarà sempre positivo. Così, nel nostro caso, il risultato della somma {(x_2 - x_1)^2+(y_2-y_1)^2} sarà sempre positivo o al più nullo.
Di conseguenza, nel radicale di indice pari {\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}} il radicando non sarà mai negativo. E quindi, in conclusione, il radicale, pur avendo indice pari, esisterà sempre a prescindere dalla particolare coppia di punti {P_1, \: P_2} scelta (vedi: condizioni di esistenza dei radicali).
Caso di due punti appartenenti ad una retta parallela ad uno degli assi coordinati
Supponiamo di avere due punti {P_1} e {P_2} del piano cartesiano tali da avere coordinate:
P_1=(a, y_1), \qquad P_2=(a, y_2)
Come possiamo vedere, i due punti condividono lo stesso valore dell’ascissa (abbiamo quindi {x_1 = x_2 = a}). Di conseguenza, i due punti appartengono ad una retta parallela all’asse {y}.
Così, nel calcolare la distanza tra i due punti ci accorgiamo che la differenza {x_2-x_1} è nulla. Pertanto, la formula della distanza tra due punti si riduce in questo caso a:
\small D(P_1, P_2) =\sqrt{(y_2-y_1)^2}, \qquad x_1=x_2 Ovvero, ricordando che in generale si ha {\sqrt{x}=|x|} (vedi proprietà dei radicali):
\small D(P_1, P_2)=|y_2-y_1|, \qquad x_1=x_2 \quad \text{(punti di uguale ascissa)}Effettivamente ritroviamo la stessa espressione che ci fornisce la formula per il calcolo della distanza tra due punti su una data retta {r}. In questo caso, infatti, la distanza tra i due punti nel piano cartesiano si riduce alla distanza tra i due stessi punti presa sulla retta {r}, parallela all’asse {y} e alla quale appartengono i due punti dati.
Ora, consideriamo due punti {P_1} e {P_2} aventi stavolta coordinate del tipo:
P_1=(x_1, b), \qquad P_2=(x_2,b)
Ci ritroviamo qui nel caso di due punti aventi la stessa ordinata, ovvero aventi la coordinata lungo l’asse {y} in comune. Adesso i due punti appartengono ad una retta parallela all’asse {x}.
In questo caso, diviene nulla la differenza {y_2-y_1} e la formula relativa alla distanza tra due punti nel piano cartesiano si riduce a:
\small D(P_1, P_2)=\sqrt{(x_2-x_1)^2}=|x_2-x_1|, \qquad y_1=y_2 \quad \small {\text{(punti di uguale ordinata)}}Distanza nel piano cartesiano tra un punto e l’origine degli assi
Ricordiamo che il punto di intersezione tra gli assi coordinati si chiama origine e nel caso di un sistema di riferimento avente due assi {x} e {y} ha coordinate:
O=(0,0)
Così, la distanza tra un punto {P(x,y)} e l’origine {O} è data da:
D(P,O)=\sqrt{(x-0)^2+(y-0)^2}=\boxed{\sqrt{x^2+y^2}}Esempi
Prima di occuparci dei casi pratici, riteniamo utile sottolineare gli accorgimenti da seguire per applicare correttamente la formula data. In particolare, è fondamentale che in ciascuna differenza nel radicando compaiano coordinate relative allo stesso asse. Attenzione dunque a non commettere errori nel sostituire i valori delle coordinate, mescolando inavvertitamente in una differenza valori relativi alle coordinate di differenti assi.
Non altera invece il risultato finale l’ordine con il quale si presentano i valori delle coordinate nella differenza. Infatti, le differenze che figurano nel radicando sono entrambe elevate al quadrato. Così, ad esempio, le quantità {(5-2)^2} e {(2-5)^2} restituiscono comunque lo stesso valore. Tuttavia, per una questione di ordine formale, è comunque necessario sostituire i valori numerici delle coordinate esattamente nello stesso ordine nel quale si presentano nella formula letterale. In altre parole, se abbiamo {x_1=3} e {x_2=1}, dovremo scrivere {(x_1-x_2)^2=(3-1)^2} e non {(x_1-x_2)=(1-3)^2}, anche se in entrambi i casi otteniamo la stessa quantità.
Vediamo ora come applicare la formula per il calcolo della distanza tra due punti nel piano cartesiano con alcuni esempi, i quali mostreranno anche le particolari attenzioni da porre nel lavorare con i segni in determinati casi.
Esempio 1
Calcolare la distanza tra i due punti del piano cartesiano {P_1=(-2,5)} e {P_2=(6, -7)}.
Ricordiamo la convenzione utilizzata per rappresentare le coordinate dei due punti in forma generale:
P_1=(x_1, y_1), \qquad P_2=(x_2, y_2)
Abbiamo di conseguenza per il caso in esame {x_1=-2, x_2=6, y_1=5, y_2=-7}. Applicando la formula:
\begin{align*} & D(P_1, P_2)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}= \\ \\ & = \sqrt{[6-(-2)]^2+(-7-5)^2}=\sqrt{(6+2)^2+(-12)^2}=\\ \\ & =\sqrt{8^2+12^2}=\sqrt{64+144}=\sqrt{208}=\end{align*}Osserviamo come un utilizzo abbondante delle parentesi sia di grande aiuto nell’evitare errori di segno, specialmente quando si ha ancora poca esperienza nell’applicare la formula.
Possiamo a questo punto scomporre il radicando in fattori e quindi sfruttare le proprietà dei radicali (vedi: semplificazione dei radicali):
=\sqrt{13 \cdot 2^{4}}=2^2 \sqrt{13} = 4\sqrt{13}Così in conclusione per la distanza tra i due punti dati sul piano cartesiano possiamo scrivere:
D(P_1, P_2)=4\sqrt{13}Esempio 2
Calcolare la distanza tra i punti {P_1=(-4,-7)} e {P_2=(-1,-2)}.
Abbiamo:
\small \begin{align*} &D(P_1, P_2)= \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\\ \\ & =\sqrt{[-1-(-4)]^2+[-2-(-7)]^2}=\sqrt{(-1+4)^2+(-2+7)^2}=\\ \\ & =\sqrt{3^2+5^2}=\sqrt{9+25}=\sqrt{34}\end{align*}Non è possibile semplificare il radicale ottenuto come risultato poiché {34} è un numero primo. Così la distanza tra i due punti dati è in conclusione esprimibile come:
D(P_1, P_2) = \sqrt{34}Esempio 3
Calcolare la distanza tra i punti del piano cartesiano {P_1=(2,3)} e {P_2=(1,7)}.
Procedendo allo stesso modo dei casi precedenti, abbiamo:
\small \begin{align*} &D(P_1, P_2) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}= \\ \\ & =\sqrt{(1-2)^2+(7-3)^2}=\sqrt{(-1)^2+(4)^2}=\sqrt{1+16}=\sqrt{17}\end{align*}Ancora, {17} è un numero primo. Quindi in conclusione:
D(P_1, P_2) = \sqrt{17}Esempio 4
Calcolare la distanza tra i punti {P_1=(4,1)} e {P_2=(7,5)}.
Si ha:
\begin{align*} &D(P_1, P_2) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}= \\ \\ & =\sqrt{(7-4)^2+(5-1)^2}=\sqrt{3^2+4^2}=\\ \\ & =\sqrt{9+16}=\sqrt{25}=5\end{align*}In questo caso abbiamo ottenuto come risultato una cifra tonda (formalmente, abbiamo potuto estrarre la radice quadrata esprimendo il risultato in forma esatta attraverso un numero intero).
In conclusione:
D(P_1, P_2) = 5
Tabella riepilogativa della formula per il calcolo della distanza tra due punti nel piano nei vari casi
Vogliamo ora riassumere le varianti della formula per il calcolo della distanza tra due punti del piano cartesiano mediante la seguente tabella:
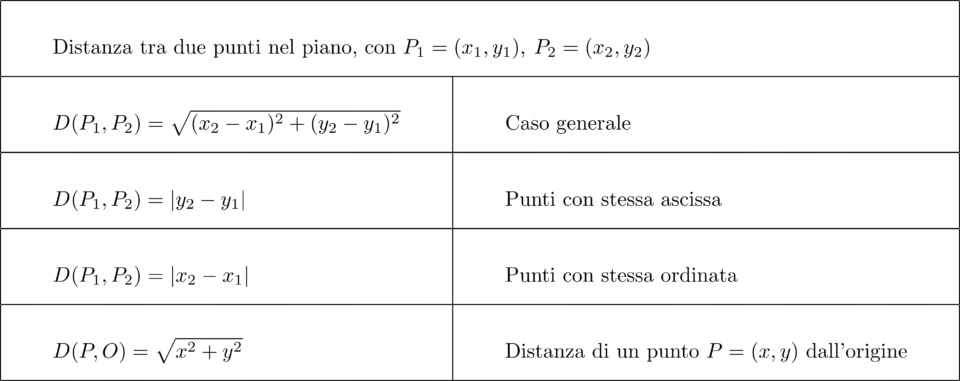
L’utilizzo della formula anche nelle sue versioni semplificate risulta in alcuni casi vantaggioso, a patto però di scegliere correttamente la formula da utilizzare di volta in volta. Tenete comunque presente che la formula generale è sempre valida.
Il seguente esempio mostra come calcolare il perimetro di una figura piana della quale sono date le coordinate di tutti i suoi vertici. La misura di ciascun lato è data proprio dalla distanza tra le opportune coppie di vertici della figura. E scegliendo di volta in volta la formula da utilizzare fra quelle proposte nella precedente tabella, sarà possibile svolgere i calcoli in modo più rapido rispetto all’adozione della sola formula generale.
Calcolo del perimetro di una figura piana a partire dalle coordinate dei suoi vertici
Calcolare il perimetro della figura piana avente per vertici i punti {A=(0,0), B=(2,5), C=(9,6), D=(9,-1)}.
Cominciamo rappresentando i vertici nel piano cartesiano, in modo da poter disegnare la figura:
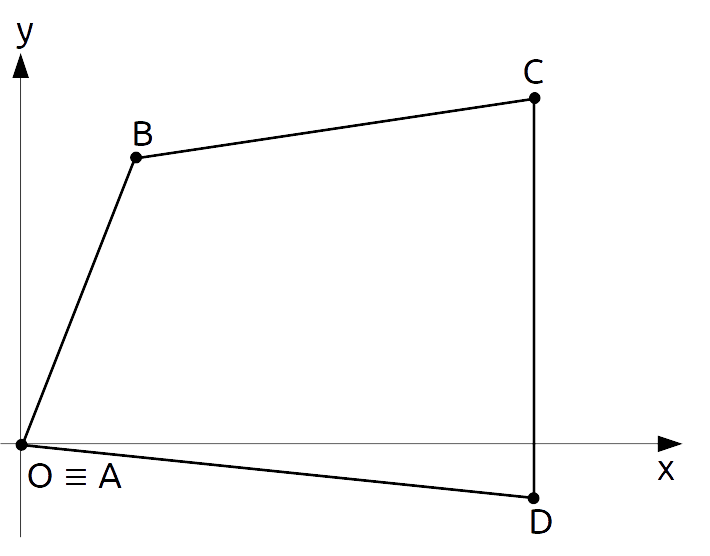
Si tratterà di calcolare le distanze {\overline{AB}, \overline{BC}, \overline{CD}, \overline{DO}}, per poi sommarle tra loro ottenendo il perimetro cercato.
Nelle formule che via via utilizzeremo indicheremo le coordinate dei vari punti riportando in pedice il punto al quale si riferisce ciascuna coordinata. Così ad esempio indicheremo il punto {A} come {A=(x_A, y_A)}, e così via.
Cominciamo con la distanza {\overline{AB}}.
Dato che il punto {A} coincide con l’origine, la distanza tra il punto {A} e il punto {B} equivale alla distanza del punto {B} dall’origine. Basterà quindi utilizzare la formula relativa alla distanza di un punto dall’origine:
\small \overline{AB}= D(B,O)=\sqrt{x_B^2+y_B^2}=\sqrt{2^2+5^2}=\sqrt{4+25}=\sqrt{29}Veniamo ora alla distanza {\overline{BC}}, che dovremo calcolare utilizzando la formula generale. Infatti, i punti {B} e {C} non condividono la stessa ascissa, non condividono la stessa ordinata e sono entrambi diversi dall’origine. Abbiamo:
\overline{BC} = \sqrt{(9-2)^2+(6-5)^2}=\sqrt{7^2+1^2}=\sqrt{50}Passiamo ora alla distanza {\overline{CD}}. Osservando che i due punti condividono la stessa ascissa, possiamo direttamente utilizzare l’opportuna formula in versione ridotta:
\overline{CD} = \sqrt{(y_D-y_C)^2}=\sqrt{(-1-6)^2}=\sqrt{(-7)^2}=\sqrt{49}=7Rimane ora soltanto da calcolare la distanza {\overline{DA}}, la quale coincide con la distanza del punto {D} dall’origine:
\overline{DA}=D(D,O)=\sqrt{x_D^2+y_D^2}=\sqrt{9^2+(-1)^2}=\sqrt{82}Infine per calcolare il perimetro della figura basta sommare tra loro tutte le distanze sin qui ottenute, le quali effettivamente rappresentano la misura di ciascun lato della figura stessa:
\small \begin{align*} & p=\overline{AB}+\overline{BC}+\overline{CD}+\overline{DA}= \\ \\ & =\sqrt{29}+\sqrt{50}+7+\sqrt{82} = \sqrt{29}+5\sqrt{2}+7+\sqrt{82}\approx \\ \\ & \approx 5,3851+ 7,071+7+9,055\approx 28,51\end{align*}Abbiamo espresso il risultato finale in forma approssimata, poiché in questo caso la forma esatta risultava un po’ ingombrante.
Disuguaglianza triangolare
Abbiamo già visto la disuguaglianza triangolare nel caso di tre punti nel riferimento cartesiano dato da una retta {r}. Vogliamo ora mostrare come riformulare tale disuguaglianza nel caso di tre punti qualsiasi del piano cartesiano.
Consideriamo allora tre punti {A, \: B, \: C} scelti arbitrariamente nel piano cartesiano:
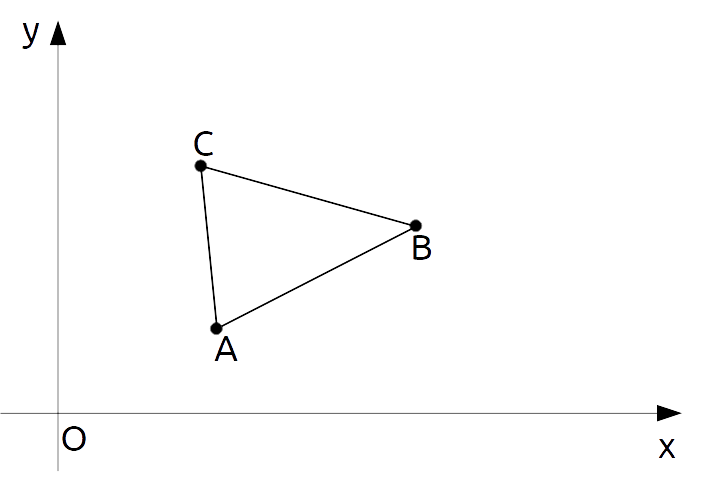
Le distanze {\overline{AB}, \overline{CB}} e {\overline{CA}} sono legate tra loro dalla seguente relazione, detta disuguaglianza triangolare, che è valida anche nel piano cartesiano:
\overline{AB} \leq \overline{AC}+\overline{CB}L’uguaglianza tra i due membri si ha se il punto {C} appartiene al segmento {\overline{AB}}.
Se consideriamo il triangolo {\stackrel{\triangle}{ABC}}, possiamo osservare come la disuguaglianza triangolare, intesa con il solo simbolo di “minore”, riflette una nota proprietà dei triangoli: la misura del lato di un triangolo è sempre minore della somma delle misure dei rimanenti lati. Consideriamo per questa particolare rilettura il solo simbolo di minore poiché, affinché si abbia un triangolo, il punto {C} non può appartenere al segmento {\overline{AB}}.
Osserviamo infine che la disuguaglianza triangolare può essere estesa considerando anche più di tre punti nel piano cartesiano.
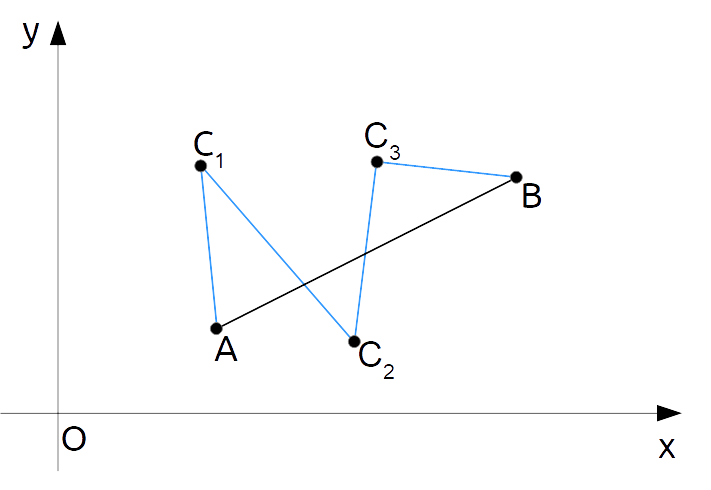
In particolare, si può dimostrare che il segmento {\overline{AB}} avrà lunghezza sempre inferiore o al più uguale alla lunghezza di una qualsiasi linea spezzata non intrecciata avente per estremi i punti {A} e {B}. Così, nel caso dei cinque punti in figura abbiamo:
\overline{AB} \leq \overline{AC_1}+\overline{C_1C_2}+\overline{C_2C_3}+\overline{C_3B}Osserviamo per maggior chiarezza che al primo membro abbiamo la misura (o lunghezza) del segmento {\overline{AB}}, mentre al secondo membro abbiamo la lunghezza della spezzata di colore azzurro in figura.
E infine, nel caso generale di {n+2} punti, la disuguaglianza diviene:
\overline{AB} \leq \overline{AC_1}+\overline{C_1C_2}+\dots + \overline{C_nB}I punti sono in questo caso {n+2} poiché abbiamo {n} punti del tipo {C_i}, con {i} numero naturale compreso tra {1} e {n} (estremi inclusi), più i due punti {A} e {B}.
Grazie alle disuguaglianze sin qui scritte siamo in grado di affermare che la linea più corta congiungente due qualsiasi punti A e B è data dal segmento {\overline{AB}}. Una qualsiasi spezzata avente per estremi i punti {A} e {B} sarà sempre più lunga o al più di lunghezza uguale a quella del segmento {\overline{AB}} (quest’ultimo caso si verifica nel caso in cui i punti {C_i} appartengano al segmento {\overline{AB}}).
Conclusioni
Per quanto riguarda come calcolare la distanza tra due punti nel piano cartesiano è tutto. Con le nozioni sin qui acquisite sarà possibile calcolare la distanza tra due qualsiasi punti del piano cartesiano utilizzando la formula più conveniente. Ricordiamo ancora una volta che la formula generale è comunque applicabile in ogni caso.
Prima di salutarci, vogliamo riportare per completezza anche la formula per il calcolo della distanza tra due punti nello spazio tridimensionale:
D(P_1, P_2) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}valida per due punti qualsiasi dello spazio tridimensionale, aventi coordinate {P_1=(x_1, y_1, z_1), \: P_2=(x_2, y_2, z_2)}. Precisiamo infine che la formula può essere immediatamente estesa anche al caso di un generico spazio {n}-dimensionale.
Nella prossima lezione vedremo come calcolare le coordinate del punto medio di un segmento giacente nel piano cartesiano. Buon proseguimento, come sempre, con SìMatematica! 🙂
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
