Punto medio di un segmento nel piano

 - 

Coordinate cartesiane e retta nel piano

Le coordinate del punto medio di un segmento del piano sono date ciascuna dalla semisomma delle coordinate, relative ad uno stesso asse, degli estremi del segmento stesso.

Dopo aver visto la definizione di punto medio di un segmento sul riferimento cartesiano dato da una retta, in questa lezione introdurremo la definizione di punto medio di un segmento nel piano cartesiano. E nel fare questo utilizzeremo quanto già sappiamo sulle coordinate cartesiane nel piano e sulla nozione di distanza tra due punti nel piano cartesiano.

Nel corso della lezione presenteremo degli esempi su come calcolare le coordinate del punto medio di un segmento del piano cartesiano, ed infine mostreremo come parametrizzare un segmento del piano. E nel fare questo, partiremo proprio dalla formula delle coordinate del punto medio di un segmento nel piano, generalizzandola in modo opportuno grazie all’utilizzo di un parametro reale.

A conclusione di questa trattazione mostreremo infine come estendere la formula per il calcolo delle coordinate del punto medio di un segmento nel piano relativamente al caso dello spazio tridimensionale.

Come calcolare le coordinate del punto medio di un segmento nel piano cartesiano

Vediamo subito come ricavare delle formule che ci permettano di calcolare le coordinate del punto medio di un segmento nel piano cartesiano. Per chi ha fretta, è possibile saltare la dimostrazione che qui a seguire presenteremo ed andare direttamente alle formule di utilizzo pratico.

Cominciamo prima di tutto rappresentando nel piano cartesiano un segmento {\overline{AB}}:

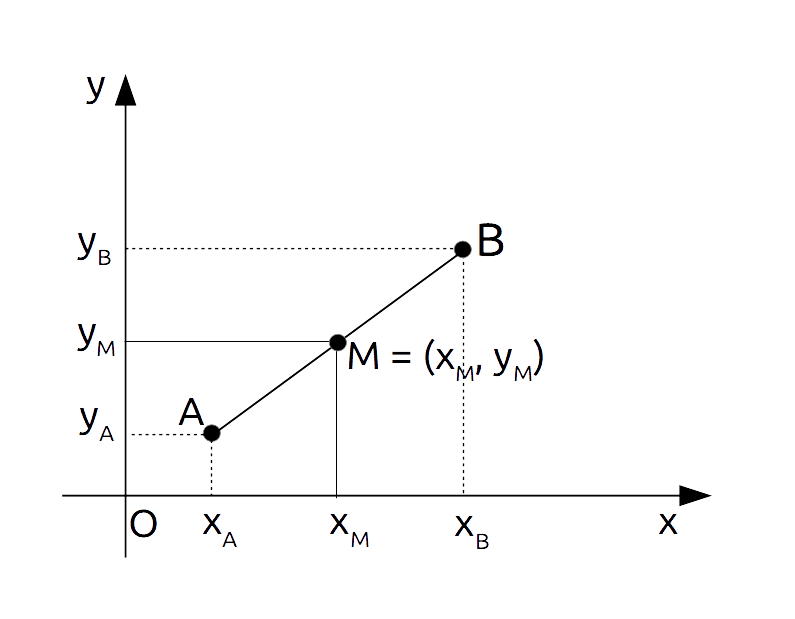
Gli estremi del segmento {\overline{AB}} sono dati da {A=(x_A, y_A)} e {B=(x_B, y_B)}. Il punto medio {M} del segmento {\overline{AB}} è invece dato da {M = (x_M, y_M)}. Per definizione, il punto medio {M} è tale da rispettare l’uguaglianza:

\overline{AM}=\overline{MB}

ove al primo membro abbiamo la lunghezza del segmento {\overline{AM}} e al secondo membro la lunghezza del segmento {\overline{MB}}. E’ importante osservare che tali lunghezze coincidono rispettivamente con le distanze {D(A, M)} e {D(M,B)} (vedi: distanza tra due punti nel piano).

Ora, il nostro obiettivo è calcolare i valori dell’ascissa {x_M} e dell’ordinata {y_M} relative al punto medio {M}.

Consideriamo la retta {r_1} parallela all’asse {y} e passante per il punto {A}, e la retta {r_2} parallela all’asse {x} e passante ancora per il punto {A}:

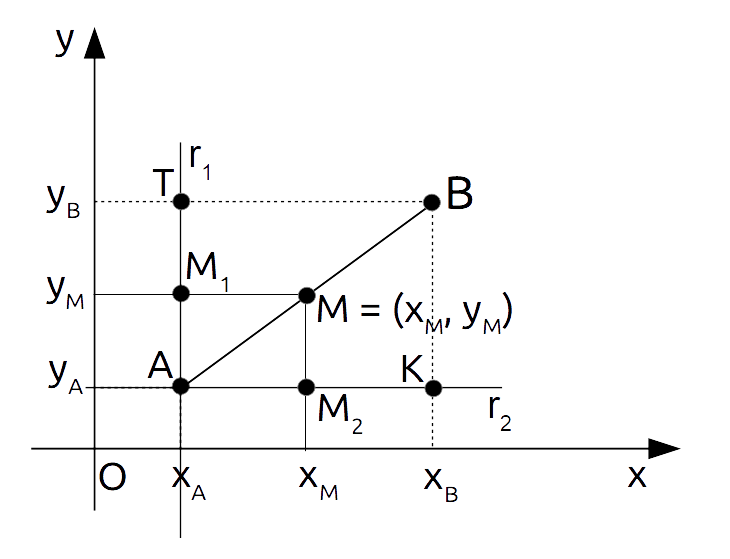
Osserviamo che i punti {M_1} ed {M_2} sono le proiezioni ortogonali del punto {M} rispettivamente sulla retta {r_1} e sulla retta {r_2}. E, per il teorema di Talete, tali punti coincidono rispettivamente con il punto medio del segmento {\overline{AT}} e con il punto medio del segmento {\overline{AK}}.

NOTA. Mostriamo per maggior chiarezza l’utilizzo del teorema di Talete in questo specifico caso. E’ in particolare di nostro interesse un corollario del teorema di Talete, il quale afferma che, in un triangolo, una retta parallela ad un qualsiasi lato del triangolo taglia proporzionalmente gli altri due lati. Così, la retta passante per i punti {M_1} ed {M} taglia a metà l’ipotenusa del triangolo {\stackrel{\triangle}{ATB}}. Allo stesso modo, anche la retta passante per i punti {M_2} ed {M} taglia a metà l’ipotenusa del triangolo {\stackrel{\triangle}{AKB}}. Di conseguenza, tali rette tagliano a metà anche il cateto {\overline{AT}} del triangolo {\stackrel{\triangle}{ATB}} e il cateto {\overline{AK}} del triangolo {\stackrel{\triangle}{AKB}}. E quindi, in conclusione, i punti {M_1} ed {M_2} sono necessariamente i punti medi dei segmenti {\overline{AT}} ed {\overline{AK}}.

Tenendo dunque conto dei punti individuati grazie alle rette {r_1} ed {r_2} come in figura, applicando la definizione di punto medio di un segmento nel riferimento dato da una retta {r} possiamo calcolare le coordinate rispettivamente dei punti {M_1} ed {M_2}.

Ripetendo per completezza la procedura descritta nella lezione del link, osserviamo che il punto {M_1}, punto medio del segmento {\overline{AT}}, deve rispettare l’uguaglianza:

AM_1 = M_1T

ovvero, riesprimendo ciascuna lunghezza algebrica utilizzando le coordinate cartesiane:

y_M-y_A=y_B-y_M

da cui, ricavando {y_M}:

2y_M = y_B+y_A \quad \Rightarrow \quad y_M=\dfrac{y_A+y_B}{2}

Procedendo allo stesso modo per il punto {M_2}, ovvero imponendo l’uguaglianza {AM_2 = M_2K}, otteniamo:

\small AM_2 = M_2 K \iff x_M-x_A=x_B-x_M \quad \Rightarrow \quad x_M=\dfrac{x_A+x_B}{2}

Di conseguenza per il calcolo delle coordinate del punto medio del segmento {\overline{AB}} sul piano cartesiano valgono le formule:

{x_M = \dfrac{x_A+x_B}{2}; \qquad y_M = \dfrac{y_A+y_B}{2}}

Abbiamo così effettuato la dimostrazione della regola per il calcolo delle coordinate del punto medio di un segmento nel piano cartesiano.

Formule per determinare il punto medio di un segmento nel piano cartesiano

Le coordinate del punto medio di un segmento nel piano cartesiano sono uguali alle semisomme delle coordinate degli estremi del segmento stesso prese lungo lo stesso asse.

In particolare, se {\overline{AB}} è un segmento del piano cartesiano di estremi {A=(x_A, y_A)} e {B=(x_B, y_B)}, il punto medio {M=(x_M, y_M)} del segmento {\overline{AB}} ha coordinate esprimibili con le formule: {\boxed{x_M = \dfrac{x_A+x_B}{2}; \qquad y_M = \dfrac{y_A+y_B}{2}}}

In parole povere, l’ascissa del punto medio di un segmento è data dalla media aritmetica delle ascisse dei suoi estremi. Allo stesso modo, l’ordinata del punto medio di un segmento è data dalla media aritmetica delle ordinate dei suoi estremi.

A questo punto, verifichiamo per completezza che le espressioni appena fornite per le coordinate del punto medio {M} nel piano soddisfano l’uguaglianza:

\overline{AM} = \overline{MB}

la quale effettivamente corrisponde alla definizione di punto medio di un segmento {\overline{AB}} nel piano cartesiano.

Ricordando la definizione di distanza tra due punti nel piano, la precedente diviene:

\sqrt{(x_M-x_A)^2+(y_M-y_A)^2} = \sqrt{(x_B-x_M)^2+(y_B-y_M)^2}

e quindi, sostituendo le espressioni per {x_M} e {y_M}:

\small \sqrt{\left( \dfrac{x_A+x_B}{2}-x_A\right)^2 +\left( \dfrac{y_A+y_B}{2}-y_A\right)^2}=\sqrt{\left(x_B-\dfrac{x_A+x_B}{2} \right)^2+\left( y_B-\dfrac{y_A+y_B}{2}\right)^2}

Effettivamente sviluppando i calcoli in ciascun membro arriviamo all’identità:

\small \sqrt{\left( \dfrac{-x_A+x_B}{2}\right)^2+\left( \dfrac{-y_A+y_B}{2}\right)^2} = \sqrt{\left( \dfrac{x_B-x_A}{2}\right)^2 + \left( \dfrac{y_B-y_A}{2}\right)^2}

e l’uguaglianza {\overline{AM}=\overline{MB}} risulta in conclusione verificata.

Presentiamo ora degli esempi relativi al calcolo delle coordinate del punto medio di un segmento nel piano cartesiano.

Esempi

Esempio 1

Calcolare il punto medio {M} di un segmento avente per estremi i punti {A=(5,10)} e {B=(-3,7)}.

Indicando con {x_M} e con {y_M} rispettivamente l’ascissa e l’ordinata del punto medio cercato abbiamo:

\begin{align*} & x_M = \dfrac{x_A+x_B}{2}=\dfrac{5+(-3)}{2}=\dfrac{5-3}{2}=\dfrac{2}{2}=1 \\ \\ & y_M = \dfrac{y_A+y_B}{2}=\dfrac{10+7}{2}=\dfrac{17}{2} \end{align*}

Attenzione! Stiamo sempre molto attenti a non mescolare ascisse ed ordinate in una stessa formula. Sostituiamo quindi i valori numerici nelle formule sempre con la massima cautela.

Così il punto medio del segmento {\overline{AB}} è in conclusione:

M=(x_M, y_M) = \left( 1, \dfrac{17}{2}\right)

Prestiamo attenzione ad indicare sempre nel corretto ordine l’ascissa e l’ordinata del punto medio.

Esempio 2

Calcolare il punto medio del segmento {\overline{AB}} con {A=(-2,-5)} e {B=(8,-3)}.

Abbiamo:

\begin{align*} &x_M = \dfrac{x_A+x_B}{2}=\dfrac{-2+8}{2}=\dfrac{6}{2}=3; \\ \\ &y_M = \dfrac{y_A+y_B}{2}=\dfrac{-5+ (-3)}{2}=\dfrac{-8}{2}=-4\end{align*}

Così abbiamo in conclusione:

M=(x_M, y_M) = (3, -4)

Parametrizzazione di un segmento (approfondimento)

A partire dalle espressioni delle coordinate del punto medio di un segmento possiamo chiederci come esprimere in forma analitica le coordinate di un generico punto di un dato segmento {\overline{AB}}.

Osserviamo che il punto medio {M} di un segmento {\overline{AB}} può essere espresso come:

\begin{align*} & M=\left( \dfrac{1}{2}(x_A+x_B), \dfrac{1}{2}(y_A+y_B)\right)=\\ \\ & =\left( \dfrac{1}{2}x_A+\dfrac{1}{2}x_B, \dfrac{1}{2}y_A+\dfrac{1}{2}y_B\right)  \end{align*}

Ciò rappresenta una rilettura piuttosto immediata delle formule per il calcolo delle coordinate del punto medio di un segmento.

Ora, si può dimostrare che un generico punto del segmento {\overline{AB}} può essere espresso come:

P=\left( \alpha x_A+\beta x_B, \alpha y_A+\beta y_B\right) \qquad *

ove {\alpha} e {\beta} sono dei parametri reali non negativi e minori o al più uguali ad {1}.

E come è immediato osservare, otteniamo dalla precedente il punto medio {M} ponendo {\alpha=\dfrac{1}{2}} e {\beta = \dfrac{1}{2}}.

Inoltre, ponendo {\alpha=1} e {\beta = 0} otteniamo sempre dalla precedente l’estremo {A} del segmento:

A=(x_A, y_A)

Allo stesso modo, ponendo {\alpha = 0} e {\beta = 1} otteniamo l’estremo {B} del segmento:

B=(x_B, y_B)

Ora, in tutti e tre i casi sin qui esaminati sussiste:

\alpha + \beta = 1

Così possiamo ad esempio scrivere:

\alpha = 1-\beta

Di conseguenza, sostituendo nella * ad {\alpha} l’espressione {1-\beta}, un punto generico del segmento {\overline{AB}} può essere scritto come:

P=\left( (1-\beta) x_A + \beta x_B, (1-\beta) y_A + \beta  y_B \right)

ove {\beta} è un numero reale tale che {\beta \in [0, 1]}.

Più avanti nel corso di queste lezioni riprenderemo la relazione appena scritta e dimostreremo che le espressioni delle coordinate del punto {P} in essa contenute effettivamente rappresentano le coordinate di punti tutti appartenenti alla retta passante per {A} e {B}, ottenibili al variare del parametro reale {\beta}. E ciò equivarrà a dimostrare che i punti che si ottengono dalla precedente relazione al variare del parametro {\beta} corrispondono ai punti del segmento {\overline{AB}}.

Così, avremo a tal punto dimostrato che la seguente:

\begin{cases} x(\beta) =(1-\beta)  x_A + \beta x_B \\ \\ y(\beta) = (1-\beta) y_A +\beta y_B\end{cases} \qquad \beta \in [0,1], \quad \beta \in \R

rappresenta una parametrizzazione del segmento {\overline{AB}}.

Siamo così riusciti a parametrizzare il segmento {\overline{AB}}, in quanto abbiamo delle espressioni per l’ascissa e l’ordinata di ciascun punto dello stesso segmento {\overline{AB}}, scritte come funzioni del parametro reale {\beta}.

Conclusioni

Per quanto riguarda come calcolare le coordinate del punto medio di un segmento nel piano cartesiano è tutto. Le formule che esprimono l’ascissa e l’ordinata del punto medio di un segmento non sono certo particolarmente complicate, e la definizione di media aritmetica è decisamente di grande aiuto nel ricordarle.

Durante la lezione abbiamo anche approfondito diverse questioni, ma sentitevi liberi di scegliere quali argomenti nei quali concentrarvi di più in base alle indicazioni del vostro insegnante e/o libro di testo. Qui abbiamo ritenuto utile soffermarci su diversi aspetti teorici nell’ottica della preparazione per i vostri studi futuri.

Dalla prossima lezione cominceremo lo studio delle rette nel piano. Buon proseguimento a tutti voi! 🙂