Distanza tra due punti sulla retta

 - 

Coordinate cartesiane e retta nel piano

Considerando un riferimento cartesiano dato da una retta r, la distanza tra due punti A e B giacenti sulla retta r è data dal valore assoluto della lunghezza algebrica AB del segmento avente come estremi gli stessi punti A e B.

Dopo aver introdotto le nozioni di coordinate cartesiane sulla retta e di punto medio di un segmento sempre sulla retta, in questa lezione introduciamo la definizione di distanza tra due punti su una retta presa come riferimento cartesiano.

Precisiamo sin d’ora che determinare la distanza tra due punti A e B sulla retta equivale a calcolare la lunghezza o misura del segmento AB.

Nel corso della lezione introdurremo in modo formale la nozione di distanza tra due punti sulla retta (come misura del segmento avente tali punti come estremi), mostreremo degli esempi ed infine presenteremo la disuguaglianza triangolare.

Definizione di distanza tra due punti sulla retta

Sia data una retta {r} che utilizziamo come sistema di riferimento cartesiano. In altre parole, le coordinate di un generico punto sulla retta {r} sono individuate dalla corrispondente ascissa {x} sulla retta {r} stessa (vedi coordinate cartesiane sulla retta).

La distanza tra due punti {A} e {B} sulla retta {r}, ove {a} e {b} sono rispettivamente le ascisse del punto {A} e del punto {B}, è data da:{d(A,B)=\overline{AB}=|b-a|}In altre parole, la distanza tra i due punti sulla retta {r} è data da {b-a} se {b \geq a}, mentre è data da {a-b} se {b \leq a}.

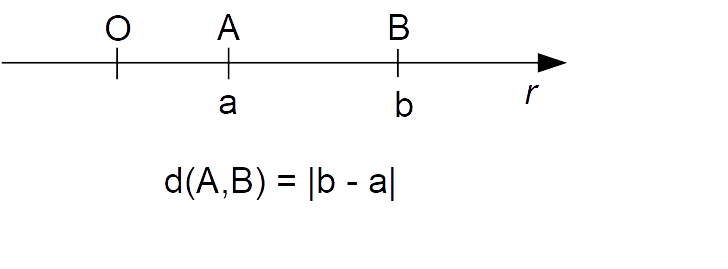
Ricordiamo che la lunghezza algebrica di un segmento {\overline{AB}} è data da {AB=b-a}, ovvero dalla differenza tra l’ascissa del secondo estremo e l’ascissa del primo estremo del segmento. Osserviamo inoltre che la quantità {|b-a|} rappresenta il valore assoluto o modulo della differenza algebrica {b-a}.

Possiamo quindi affermare che la distanza tra due punti sulla retta è data dal valore assoluto della lunghezza algebrica del segmento avente per estremi i due punti stessi.

Importante. Dato un segmento {\overline{AB}} oppure dato un segmento {\overline{BA}}, la distanza o misura tra i due estremi {A} e {B} avrà comunque lo stesso valore.
Diversamente, la lunghezza algebrica del segmento {\overline{AB}} è di segno opposto rispetto alla lunghezza algebrica del segmento {\overline{BA}}.

Esempio

Dati i due punti {A=(2)} e {B=(7)} sul riferimento cartesiano dato da una retta {r}, la distanza tra i due punti si calcola come:

D(A,B)=\overline{AB}=|b-a|=|7-2|=|5|=5

Osserviamo che tale distanza si calcola anche come segue:

D(B,A)=\overline{BA}=|a-b|=|2-7|=|-5|=5

Otteniamo lo stesso risultato a prescindere dall’ordine con il quale consideriamo i punti, grazie alla presenza del valore assoluto.

Significato geometrico del valore assoluto di un numero

Dalla definizione appena data segue che:

\overline{OA}=|a-0|=|a|

ove {0} è l’ascissa dell’origine {O}.

Di conseguenza, possiamo concludere che il valore assoluto di un numero reale {a} rappresenta la distanza del punto {A} dall’origine. E questo è il legame tra il valore assoluto di un numero e la distanza tra due punti sulla retta.

Distanza tra due punti sulla retta e disuguaglianza triangolare

Dati tre punti {A}, {B} e {C} sulla retta {r}, aventi ascisse rispettivamente {a, \:b, \: c}, vale la seguente relazione detta disuguaglianza triangolare:

|b-a| \leq |b-c| +|c-a|

Grazie alla definizione di lunghezza o misura del segmento {\overline{AB}}, possiamo giustificare la disuguaglianza triangolare dal punto di vista geometrico.

Supponiamo come primo caso che il punto {C} si trovi tra il punto {A} e il punto {B}:

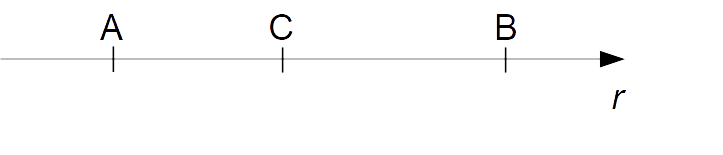
In tal caso fra le lunghezze {\overline{AC}}, {\overline{CB}} e {\overline{AB}} vale la relazione:

\overline{AB}=\overline{AC}+\overline{CB}

Osserviamo che possiamo riscrivere la relazione utilizzando le coordinate cartesiane dei punti {A}, {B} e {C}, sfruttando la definizione di lunghezza di un segmento. Abbiamo:

|b-a|=|c-a|+|b-c|

ovvero, riordinando i termini al secondo membro:

|b-a|=|b-c|+|c-a|

In questo modo risulta effettivamente verificata la disuguaglianza triangolare (questa infatti ammette anche l’uguaglianza tra i due membri della disuguaglianza stessa).

Invece, supponiamo che il punto {C} segua i due punti {A} e {B}:

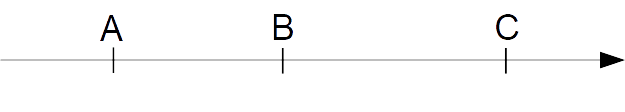
In questo caso, evidentemente si ha:

\overline{AB} < \overline{AC}+\overline{CB}

ovvero, utilizzando ancora le ascisse dei punti {A, \: B, \: C}:

|b-a| < |c-a|+|b-c|

ossia, riordinando i termini al secondo membro:

|b-a|<|b-c|+|c-a|

Di conseguenza, anche in questo caso la disuguaglianza triangolare risulta soddisfatta.

In modo del tutto simile si può infine mostrare geometricamente che la disuguaglianza triangolare è soddisfatta anche nel caso in cui il punto {C} si trovi nella retta {r} prima dei punti {A} e {B}:

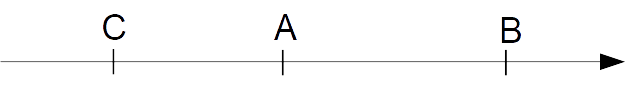
Infatti abbiamo anche in quest’ultimo caso:

\overline{AB} < \overline{AC}+\overline{CB}

Per quanto riguarda la distanza tra due punti sulla retta è tutto. Nella prossima lezione introdurremo le coordinate cartesiane nel piano, per poi ridefinire la distanza tra due punti nel caso del piano. Buono studio a tutti voi!