Le coordinate cartesiane sulla retta consentono di individuare univocamente un qualsiasi punto di una data retta r associando ad esso un valore numerico. In tal modo è possibile rappresentare sulla retta i numeri reali. L’idea è quella di associare a ciascun numero reale un punto della retta e viceversa, creando così una corrispondenza biunivoca tra l’insieme dei numeri reali e i punti di una data retta r.
Il fatto che sia possibile rappresentare su una retta tutti i numeri reali compresi anche quelli irrazionali ci viene assicurato dal postulato di Dedekind, secondo il quale per ogni successione di segmenti incapsulati tra loro (ovvero tali che il segmento successivo ha tutti i suoi punti in comune con il segmento precedente) esiste almeno un punto in comune a tutti i segmenti. Semplificando, tale postulato assicura la continuità della retta: dati due punti appartenenti ad una retta, esiste sempre almeno un punto compreso tra i due stessi punti.
La possibilità di poter in generale rappresentare un insieme numerico mediante una retta ci viene invece assicurata dal postulato di Archimede, per il quale dati due segmenti di differente lunghezza e non degeneri (ovvero non riducibili ad un solo punto) esiste sempre un numero naturale {n} tale che il suo prodotto per la lunghezza del segmento minore supera la lunghezza del segmento maggiore. Così, come vedremo tra un istante, stabilita un’opportuna unità di misura è possibile misurare un qualsiasi segmento appartenente alla retta.
Coordinate cartesiane sulla retta: sistema di riferimento o sistema di ascisse
Consideriamo una retta {r} e fissiamo su di essa un particolare punto {O} detto origine. Scegliamo inoltre un punto {U}, e prendiamo la lunghezza del segmento {\overline{OU}} come unità di misura. Utilizzeremo tale lunghezza, che indichiamo con {u}, per misurare un qualunque segmento della retta {r}.
L’origine {O} divide la retta {r} in due semirette. Indicheremo come positiva la semiretta ove giace il punto {U}, mentre indicheremo come negativa l’altra semiretta.
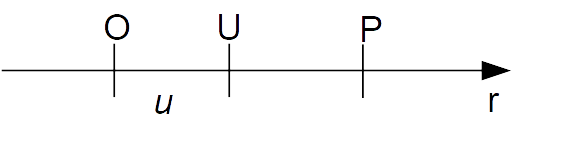
In questo modo abbiamo introdotto su {r} un riferimento cartesiano o sistema di ascisse. Il termine “sistema di ascisse” è dovuto al fatto che con tale riferimento è possibile associare ad ogni punto un numero reale (valore dell’ascissa) e viceversa ad ogni numero reale è possibile associare un numero.
E’ importante osservare che l’estremità a punta della retta {r} indica la direzione positiva, ovvero la direzione procedendo lungo la quale si finisce con l’incontrare punti di {r} aventi ascissa sempre positiva. Ciò sarà chiaro tra un istante.
Ora, scegliamo un punto {P} della retta {r}, come in figura. E’ possibile associare al punto {P} un numero reale detto ascissa {x}. Tale numero sarà positivo se il punto {P} si trova nella semiretta positiva, negativo se il punto {P} si trova invece sulla semiretta negativa. Il modulo o valore assoluto dell’ascissa {x} è dato dalla misura rispetto all’unità {u} del segmento {\overline{OP}}.
In altri termini, abbiamo:
|x|=\dfrac{\overline{OP}}{u}, \qquad \text{con} \quad u=\overline{OP}Ciò rappresenta una diretta applicazione del postulato di Archimede. Infatti, per tale postulato si ha {n \cdot u > \overline{OP}} da un certo {n \in \N} in poi. Di conseguenza, ha sicuramente senso chiedersi quante volte l’unità di misura scelta è contenuta nella lunghezza del segmento {\overline{OP}}.
Inoltre, la scrittura:
P=(x)
oppure:
P(x)
viene utilizzata per indicare che il punto {P} della retta {r} ha ascissa {x}.
Lunghezza algebrica di un segmento
Ora che abbiamo stabilito un sistema di riferimento cartesiano per la retta {r}, è possibile determinare la lunghezza algebrica di un segmento orientato costruito nella retta {r}.
Fissati due punti {A=(a)} e {B=(b)} nella retta {r}, con {a, \: b \in \R}, indichiamo con {\overline{AB}} il segmento orientato che va da {A} a {B}, mentre indichiamo con {\overline{BA}} il segmento orientato che va da {B} ad {A}.
I punti {A} e {B} si dicono estremi del segmento {\overline{AB}} o del segmento {\overline{BA}}. In particolare, nel segmento {\overline{AB}} il punto {A} è il primo estremo mentre il punto {B} è il secondo estremo.
La lunghezza algebrica {AB} di un segmento orientato {\overline{AB}} è la differenza tra l’ascissa dell’estremo {B} e l’ascissa dell’estremo {A}, ovvero è la differenza tra l’ascissa del secondo estremo e l’ascissa del primo estremo.
Se {B} segue {A} nel verso positivo fissato sulla retta {r}, allora abbiamo che {AB=b-a>0}. E sempre sotto tale ipotesi, avremo {BA=a-b < 0}.
Osserviamo che comunque entrambi i segmenti {\overline{AB}} e {\overline{BA}} hanno in valore assoluto la stessa lunghezza, ovvero {\overline{AB}=\overline{BA}}. Così, per le lunghezze algebriche rispettivamente dei segmenti {AB} e {BA} dovrà necessariamente valere la seguente relazione:
AB=-BA
o il che è lo stesso:
AB+BA=0
Esempio sul calcolo della lunghezza algebrica di segmenti
Siano dati i punti {A=(-3), \: B=(1)} e {C=(4)} su una retta {r}. Calcolare la lunghezza algebrica di ciascun segmento {\overline{AB}, \: \overline{BC}, \: \overline{AC}}.
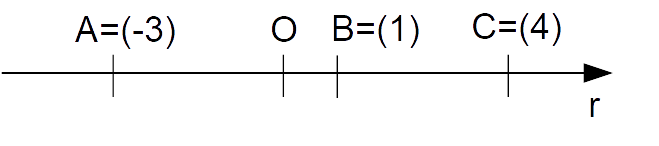
Abbiamo:
\begin{align*} & AB = 1-(-3)=1+3=4 \\ \\ &BC = 4-1=3 \\ \\ &AC=4-(-3)=4+3=7\end{align*}Relazione di Chasles
Consideriamo un riferimento cartesiano dato da una retta {r} sulla quale sia stata fissata una certa unità di misura {u}.
Scegliamo a piacere sulla retta {r} tra punti distinti {A, \: B, \: C}, ed individuiamo tramite essi, sulla retta {r}, i segmenti {\overline{AB}, \: \overline{BC}} e {\overline{AC}}. Tra le lunghezze algebriche di tali segmenti vale la relazione:
AB+BC=AC
ovvero:
AB+BC-AC = 0
e poiché {AC=-CA}:
\boxed{AB+BC+CA=0}La relazione tra le lunghezze algebriche dei segmenti orientati {\overline{AB}, \: \overline{BC} } e {\overline{CA}} appena scritta è nota come relazione di Chasles.
La dimostrazione della relazione di Chasles è piuttosto immediata e si ottiene in particolare applicando la definizione di lunghezza algebrica di un segmento orientato. Infatti abbiamo:
AB=b-a, \quad BC=c-b, \quad CA=a-c
Così la relazione di Chasles diviene:
b-a+c-b+a-c=0
che effettivamente è un’identità (i monomi al primo membro si cancellano tutti tra loro).
Per quanto riguarda le coordinate cartesiane sulla retta è tutto. Nella prossima lezione daremo la definizione di punto medio di un segmento. Un saluto e buon proseguimento a tutti voi! 🙂
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
