Condizioni di esistenza dei radicali

 - 

Radicali

In questa lezione ci occupiamo delle condizioni di esistenza dei radicali, ovvero le condizioni per le quali ha significato un radicale il cui radicando è una quantità variabile. Ci occuperemo cioè di radicali aventi all’interno della radice dei polinomi o comunque delle espressioni che dipendono dalla variabile {x} (o in generale dalla particolare variabile considerata).

Nel definire le condizioni di esistenza dei radicali dovremo distinguere i due casi di indice della radice pari o dispari. In particolare, se l’indice è pari dovremo imporre il radicando maggiore o uguale a zero. Infatti, come sappiamo dalla precedente lezione non è possibile estrarre la radice con indice pari di una quantità negativa. Così, dovremo considerare i soli valori della variabile per i quali l’espressione all’interno della radice è positiva o al più nulla.

Se invece l’indice della radice è dispari il radicando potrà anche essere negativo e di conseguenza non dovremo imporre la precedente condizione.

In entrambi i casi, tuttavia, per stabilire le condizioni di esistenza dei radicali dovremo anche considerare le condizioni di esistenza del radicando in sé per sé. In altre parole, dovremo sempre verificare se l’espressione nella variabile {x} contenuta all’interno del simbolo di radice ha senso per tutti i valori della {x} oppure no, e nel caso determinarne il campo di esistenza.

Ma vediamo subito come stabilire le condizioni di esistenza dei radicali nel caso in cui il radicando sia una quantità variabile.

Condizioni di esistenza dei radicali con radicando uguale ad un polinomio

Per capire come determinare le condizioni di esistenza dei radicali con radicando variabile cominciamo a studiare il caso relativo a radicali del tipo:

\sqrt[n]{P(x)}

ove {P(x)} è un polinomio.

Se l’indice della radice {n} è pari, dovremo imporre la condizione:

P(x) \geq 0

In tal modo escludiamo che il radicando sia negativo. Ciò si rende necessario poiché, come sappiamo, non è possibile estrarre la radice con indice pari di un numero negativo.

Se invece l’indice del radicale è dispari non dovremo imporre alcuna condizione. Infatti un polinomio è sempre definito per tutti i valori della variabile in esso presente.

Esempi

Esempio 1

Determinare le condizioni di esistenza del seguente radicale (radicali di polinomi):

\sqrt{x^2+2x-3}

L’indice della radice è {2} (quindi pari), di conseguenza dobbiamo imporre la condizione:

x^2+2x-3 \geq 0

Per risolvere la disequazione conviene scomporre il polinomio al primo membro e quindi studiare il segno dei fattori. Abbiamo (regola del trinomio caratteristico):

x^2+2x-3=(x+3)(x-1)

Di conseguenza possiamo riscrivere la precedente disequazione come:

(x+3)(x-1) \geq 0

A questo punto dobbiamo studiare il segno dei singoli fattori in modo da vedere quando il prodotto al primo membro è positivo o al più nullo. Si tratterà in particolare di applicare le regole dell’algebra elementare per determinare il segno del prodotto dei fattori (ad esempio, meno per meno dà più, più per meno dà meno, ecc.). In tal modo sarà possibile studiare il segno del polinomio sotto radice.

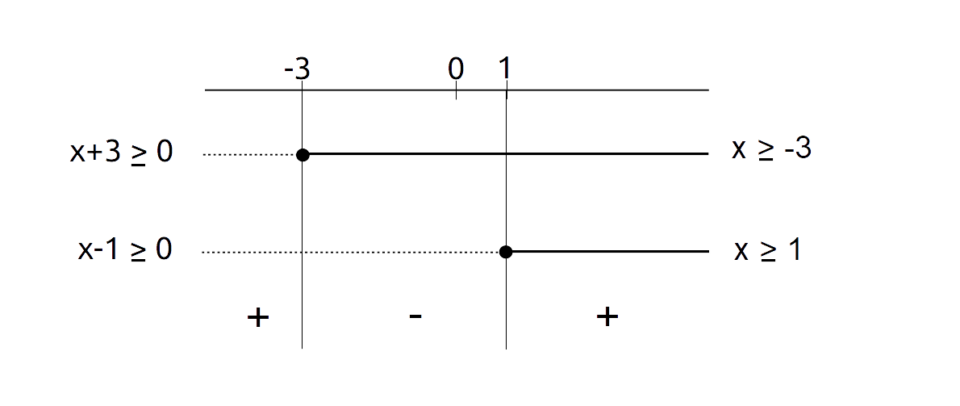
Concludiamo che il polinomio all’interno della radice è positivo o nullo per {x \leq -3} o per {x \geq 1}. Infatti come possiamo vedere dal diagramma per tali valori della {x} i fattori relativi alla scomposizione del polinomio sotto radice sono concordi (hanno lo stesso segno). E il prodotto tra due quantità aventi lo stesso segno è positivo.

Infine, osserviamo che il polinomio di suo è definito come ogni polinomio per tutti i valori reali. Di conseguenza, non dobbiamo aggiungere ulteriori condizioni di esistenza per il radicale.

Per cui in conclusione le condizioni di esistenza per il radicale {\sqrt{x^2+2x-3}} sono:

x  \leq -3 \quad \vee \quad x \geq 1

Osservazione. Ricordiamo che il simbolo “{\vee}” significa “oppure”.

Esempio 2

Determinare le condizioni di esistenza del seguente radicale (radicali di polinomi):

\sqrt[3]{x-7}

Osserviamo che l’indice del radicale è dispari. Di conseguenza, il radicando potrà essere indifferentemente positivo, negativo o nullo. E infine, dato che il polinomio è definito per ogni valore reale della {x}, concludiamo che il radicale è definito per ogni valore reale.

Condizioni di esistenza per i radicali con radicando uguale ad un rapporto tra polinomi

Consideriamo ora radicali il cui radicando è un rapporto tra polinomi. Passiamo così ad occuparci di radicali della forma:

\sqrt[n]{\dfrac{P_1(x)}{P_2(x)}}

ove {P_1(x)} e {P_2(x)} sono due polinomi nella variabile {x}. Vediamo come dobbiamo determinare in questo caso le condizioni di esistenza del radicale.

Se {n} è pari, dovremo anzitutto imporre la condizione che il radicando sia positivo o al più nullo:

{\dfrac{P_1(x)}{P_2(x)}} \geq 0

Inoltre, dovremo anche assicurarci che il rapporto tra polinomi di per sé abbia significato, ovvero che il denominatore {P_2(x)} sia diverso da zero:

P_2(x) \neq 0

Così nel caso di indice del radicale pari abbiamo in conclusione:

\small \sqrt[n]{\dfrac{P_1(x)}{P_2(x)}} \quad \text{con} \:n \: \textbf{pari}  \: \text{esiste} \:\:\iff \:\: \dfrac{P_1(x)}{P_2(x)} \geq 0 \: \wedge \:P_2(x) \neq 0

Osservazione. Ricordiamo che la doppia freccia si legge “se e solo se”. In particolare, utilizzando tale scrittura intendiamo dire che la condizione a sinistra della freccia è soddisfatta soltanto se è verificata la condizione a destra della freccia e viceversa.
Inoltre, ricordiamo che il simbolo “{\wedge}” significa “e contemporaneamente”.

Richiediamo quindi che siano soddisfatte contemporaneamente le due condizioni di radicando maggiore o uguale a zero e di polinomio al denominatore diverso da zero.

Se invece l’indice del radicale è dispari, il radicando può essere indifferentemente positivo, nullo o negativo. Di conseguenza dovremo soltanto imporre la condizione relativa al denominatore diverso da zero. Così abbiamo:

\small \sqrt[n]{\dfrac{P_1(x)}{P_2(x)}} \quad \text{con} \:n \: \textbf{dispari}  \: \text{esiste} \:\:\iff \:\: \:P_2(x) \neq 0

Esempi

Esempio 3

Determinare le condizioni di esistenza del seguente radicale (radicali con un rapporto tra polinomi):

\sqrt[4]{\dfrac{x-8}{x+2}}

Siamo in presenza di un radicale con indice pari. Di conseguenza, dovremo imporre sia la condizione di radicando positivo o al più nullo, sia imporre la condizione di esistenza del radicando di per sé (denominatore diverso da zero). Così dovranno valere contemporaneamente entrambe le condizioni:

\dfrac{x-8}{x+2} \geq 0  \quad \wedge \quad x+2 \neq 0

Per formulare in modo esplicito tali condizioni dobbiamo rispettivamente studiare il segno della frazione algebrica {\dfrac{x-8}{x+2}} ed escludere la soluzione dell’equazione {x+2=0}.

Per lo studio del segno della frazione algebrica occorre studiare separatamente il segno del numeratore e del denominatore, determinando poi con l’algebra dei segni il segno della frazione algebrica (ad esempio, meno diviso meno dà più, meno diviso più dà meno, ecc.).

Possiamo in realtà esprimere contemporaneamente entrambe le condizioni di esistenza del radicale escludendo nello studio del segno il valore che annulla il denominatore (soluzione dell’equazione {x+2=0}, ovvero {x=-2}). In pratica nello studio del segno si tratta di imporre il denominatore maggiore di zero (e non maggiore o uguale a zero). Abbiamo:

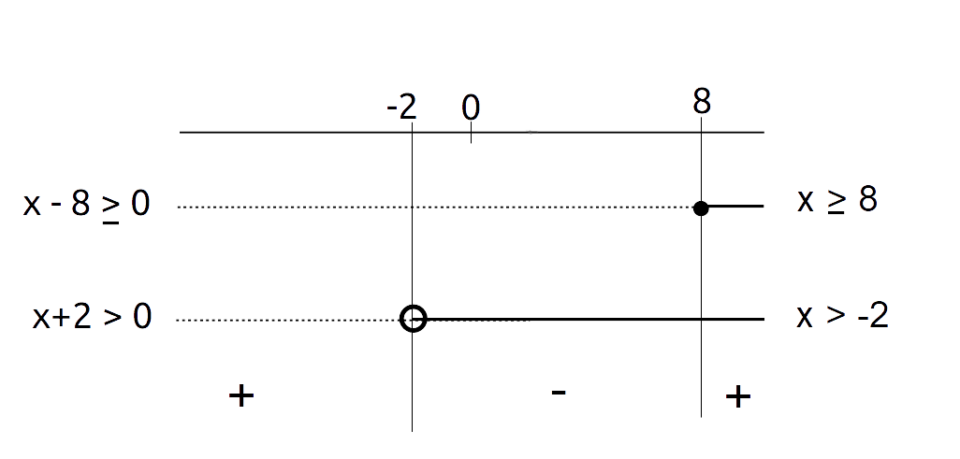
Come è possibile notare abbiamo escluso il valore che annulla il denominatore della frazione algebrica all’interno della radice. Il corrispondente punto è infatti evidenziato con un pallino vuoto.

Il radicale ha quindi significato per tutti i valori della {x} per cui la frazione algebrica è positiva o al più nulla, escludendo il valore {x=2} per il quale la frazione stessa è priva di significato.

Le condizioni di esistenza del radicale sono dunque:

x < -2 \quad \vee \quad x \geq 8

Esempio 4

Determinare le condizioni di esistenza del radicale (radicali con un rapporto tra polinomi):

\sqrt[3]{\dfrac{x^2-4}{2x+7}}

Poiché l’indice della radice è dispari, il radicando può essere indifferentemente positivo, negativo o nullo. Di conseguenza, per definire le condizioni di esistenza del radicale dovremo soltanto escludere i valori della {x} che annullano il denominatore della frazione all’interno della radice:

2x+7 \neq 0 \quad \iff \quad 2x \neq -7 \quad \iff \quad x \neq -\dfrac{7}{2}

Così in conclusione la condizione di esistenza del radicale è {x \neq -\dfrac{7}{2}}.

Condizioni di esistenza di espressioni contenenti radicali

E’ infine interessante prendere in esame il caso di espressioni contenenti radicali. Ad esempio, supponiamo di voler determinare le condizioni di esistenza della seguente espressione:

\sqrt{x+3}-\sqrt[3]{\dfrac{x+2}{x-6}}

Affinché l’espressione abbia significato tutti i radicali presenti nell’espressione dovranno a loro volta avere significato. Così in parole povere dovremo studiare il campo di esistenza per ciascun radicale (secondo le regole appena viste) e quindi imporre contemporaneamente entrambe le corrispondenti condizioni di esistenza.

Così, il radicale {\sqrt{x+3}} è un radicale di un polinomio con radice avente indice pari, e di conseguenza dovremo imporre tale polinomio maggiore o al più uguale a zero:

x+3 \geq 0 \quad \iff \quad x \geq -3

e questa è una prima condizione di esistenza per l’espressione data.

Veniamo ora al secondo radicale. Trattandosi di un radicale con indice dispari il radicando può essere positivo, negativo o nullo. L’unica cosa di cui dobbiamo preoccuparci è che l’espressione all’interno della radice abbia significato. Così dobbiamo imporre il denominatore della frazione algebrica all’interno della radice diverso da zero:

x-6 \neq 0 \quad \iff \quad x \neq 6

In conclusione mettendo insieme le condizioni scritte otteniamo per l’espressione di partenza le condizioni di esistenza:

x \geq -3 \quad \wedge \quad x \neq 6

Ricordiamo ancora che il simbolo “{\wedge}” significa “e contemporaneamente”. Così abbiamo imposto contemporaneamente tutte le condizioni di esistenza dei radicali presenti nell’espressione.

Conclusioni

Per quanto riguarda lo studio delle condizioni di esistenza dei radicali è tutto. Nella prossima lezione ci occuperemo dello studio delle funzioni radice quadrata e radice cubica. Nella lezione ancora successiva introdurremo invece la proprietà invariantiva dei radicali. Buono studio con SìMatematica.