Esercizi sulle condizioni di esistenza dei radicali

 - 

Radicali

In questa scheda presentiamo degli esercizi svolti sulle condizioni di esistenza dei radicali. A partire cioè da radicali con radicando dipendente da una variabile, il nostro obiettivo è capire per quali valori della variabile esiste ciascun radicale.

Come già evidenziato nella lezione teorica, distingueremo tra radicali con indice pari e radicali con indice dispari. Nel caso di radicali con indice pari, dovremo imporre le opportune condizioni affinché il radicando sia maggiore o al più uguale a zero. Ciò non è invece richiesto se l’indice del radicale considerato è dispari. Ma in generale per gli esercizi sulle condizioni di esistenza dei radicali dovremo sempre stabilire per quali valori della variabile l’espressione all’interno della radice ha significato.

Così ad esempio se all’interno della radice, qualunque sia il suo indice, ci ritroviamo con un denominatore che dipende dalla variabile, dovremo escludere i valori della variabile stessa che annullano il denominatore. Dovremo cioè stabilire per quali valori della {x} la frazione all’interno della radice ha significato. E le condizioni relative al denominatore non nullo così determinate dovranno valere contemporaneamente alle eventuali condizioni sulla non negatività del radicando (nel caso di radicali con indice pari).

Ci occuperemo infine anche dello studio delle condizioni di esistenza di espressioni contenenti radicali.

Fatte le dovute premesse, vediamo subito questa serie di esercizi sulle condizioni di esistenza dei radicali.

Esercizi svolti e commentati sulle condizioni di esistenza dei radicali

Prima parte: radicandi dati da polinomi

Esercizio 1

Determinare le condizioni di esistenza del radicale:

\sqrt[3]{x-4}

Osserviamo che l’indice del radicale è dispari. Di conseguenza, il radicando (ovvero il polinomio {x-4}) potrà essere indifferentemente positivo, negativo o nullo. E poiché un polinomio esiste per ogni valore reale della {x}, concludiamo che anche il radicale dato esiste per ogni valore reale della {x}.

Esercizio 2

Determinare le condizioni di esistenza del radicale:

\sqrt{2x+3}

Osserviamo che siamo in presenza di un radicale con indice pari (una radice quadrata è una radice con indice {2}). Così dobbiamo assicurarci che quanto contenuto all’interno della radice, ovvero il radicando {2x+3}, sia maggiore o al più uguale a zero. Così dovremo imporre per il radicale la seguente condizione di esistenza:

2x+3 \geq 0

Per il resto non abbiamo altre condizioni da porre poiché un polinomio è definito per tutti i valori reali della variabile.

Così abbiamo:

2x+3 \geq 0 \iff x \geq -\dfrac{3}{2}

e questa è la condizione di esistenza del radicale dato.

Esercizio 3

Determinare le condizioni di esistenza del seguente radicale:

\sqrt[7]{x^2+5x}

Come nel primo esercizio, anche questo radicale è definito per ogni valore reale della {x}. Infatti, il radicale ha esponente dispari e di conseguenza il radicando può essere indifferentemente negativo, positivo o nullo.

Stiamo dunque attenti in casi di questo tipo a non studiare inutilmente il segno del radicando.

Esercizio 4

Determinare le condizioni di esistenza di:

\sqrt[8]{(2x-1)^3}

Il radicale ha indice pari e di conseguenza dovremo imporre la condizione:

(2x-1)^3 \geq 0

L’esponente del radicando è dispari e quindi basterà studiare il segno della base. Infatti la potenza con esponente dispari di un numero negativo è ancora un numero negativo. Dobbiamo quindi imporre:

2x-1 \geq 0 \iff x \geq \dfrac{1}{2}

E questa è la condizione di esistenza del radicale dato.

Esercizio 5

Determinare le condizioni di esistenza del seguente radicale:

\sqrt[4]{(x-3)^2}

Il radicale ha indice pari e quindi in teoria occorre imporre il radicando non negativo. Tuttavia, in questo particolare caso il radicando è una potenza con esponente pari. Di conseguenza, il radicando sarà sempre positivo a prescindere dal segno della base {x-3} del radicando . Così in conclusione il radicale esiste per ogni valore reale della {x}.

Seconda parte: radicandi dati da frazioni algebriche (rapporti tra polinomi)

Esercizio 6

Studiare il campo di esistenza (determinare le condizioni di esistenza) del seguente radicale:

\sqrt[5]{\dfrac{1}{x-2}}

Osserviamo che poiché il radicale ha indice dispari il radicando può assumere segno qualsiasi. Dato che però ci ritroviamo all’interno della radice con una frazione, dobbiamo escludere i valori per i quali si annulla il denominatore della stessa frazione. Nel nostro caso dovremo imporre la condizione:

x-2 \neq 0 \iff x \neq 2

Dunque il radicale esiste per tutti i valori reali della {x} tranne {2}.

Esercizio 7

Studiare il campo di esistenza del radicale:

\sqrt{\dfrac{2-x}{x+5}}

Il radicale ha indice pari, di conseguenza dovremo imporre la condizione:

\dfrac{2-x}{x+5} \geq 0 

Pretendiamo cioè che il radicando sia non negativo.

Inoltre, affinché il radicale esista, dovrà esistere anche la frazione all’interno della radice. Di conseguenza, dovremo anche imporre diverso da zero il denominatore della frazione stessa:

x+5 \neq 0 \iff x \neq - 5

Così il radicale dato esisterà soltanto se valgono contemporaneamente le seguenti condizioni:

\dfrac{2-x}{x+5} \geq 0  \quad \wedge \quad x \neq -5

Ricordiamo che il simbolo {\wedge} significa “e contemporaneamente”. E’ anche possibile in alternativa racchiudere le due condizioni che devono valere contemporaneamente entro una parentesi graffa, con lo stesso significato:

\begin{cases}  \dfrac{2-x}{x+5} \geq 0  \\ \\  x \neq -5 \end{cases}

Dobbiamo quindi prendere come insieme di definizione del radicale (che rappresenta l’insieme dei valori della {x} per i quali il radicale esiste) il particolare insieme dato dai valori per i quali la frazione dentro la radice è positiva o al più nulla, escludendo il valore che ne annulla il denominatore.

Per lo studio del segno della frazione, possiamo procedere per via algebrica o per via grafica. Nel prima caso, osserviamo che la frazione sarà positiva se il numeratore e il denominatore hanno lo stesso segno:

\begin{cases} 2-x \geq 0 \\ \\ x+5 > 0\end{cases} \quad \vee \quad \begin{cases} 2-x < 0 \\ \\ x+5 < 0\end{cases}

e quindi:

\begin{cases} x \leq 2 \\ \\ x > - 5\end{cases} \quad \vee \quad \begin{cases}x > 2 \\ \\ x < -5  \end{cases}

ovvero:

-5 < \: x \leq 2

e questa è la condizione di esistenza per il radicale.

Osserviamo che abbiamo tenuto conto della condizione {x \neq 5} escludendo l’uguaglianza nelle condizioni relative al denominatore {x+5}.

Più diretto è sicuramente lo studio del segno della frazione per via grafica, che è l’alternativa più comunemente usata per lo studio dei segni delle frazioni:

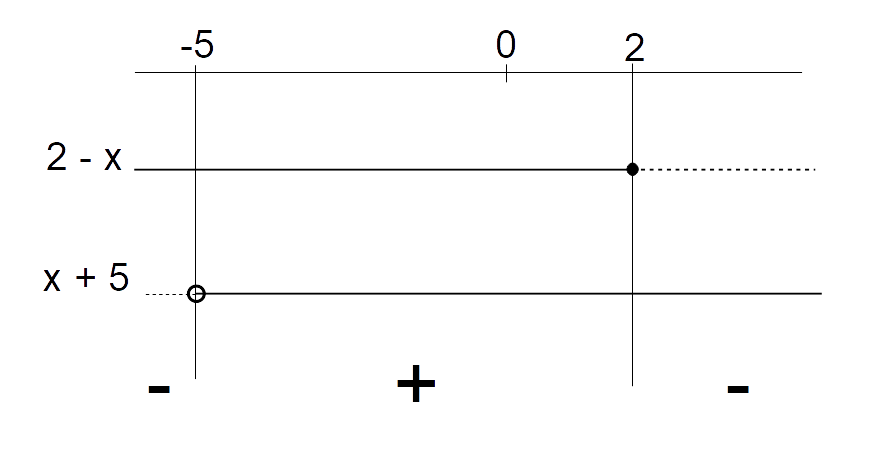
Ritroviamo così la condizione di esistenza per il radicale:

-5< x \leq 2

Esercizio 8

Veniamo all’ultimo di questi esercizi sulle condizioni di esistenza dei singoli radicali. Passeremo poi agli esercizi relativi alle espressioni con i radicali.

Studiare il campo di esistenza del seguente radicale:

\sqrt[3]{\frac{2x^2}{6-x}}

Il radicale ha indice dispari. Di conseguenza il radicando può essere indifferentemente positivo, negativo o nullo. Dobbiamo però escludere i valori per i quali la frazione non è definita, ovvero i valori che ne annullano il denominatore. Imponiamo allora la condizone:

6-x \neq 0

Da cui otteniamo:

x \neq 6

e questa è la condizione di esistenza del radicale dato.

Terza parte: condizioni di esistenza relative ad espressioni contenenti radicali

Esercizio 9

Determinare le condizioni di esistenza dell’espressione con radicali:

\sqrt{x+1}+\sqrt{x^2-1}

Poiché entrambi i radicali sono con indice pari, dovranno valere le condizioni:

x+1 \geq 0 \quad \wedge \quad x^2-1 \geq 0

Con l’operatore “{\wedge}” intendiamo dire che le condizioni dovranno valere contemporaneamente.

Dalla prima condizione otteniamo:

x+1 \geq 0 \iff x \geq -1

Per la seconda condizione, scomponiamo anzitutto il polinomio al primo membro della disuguaglianza:

x^2-1 \geq 0 \iff (x-1)(x+1) \geq 0

A questo punto dobbiamo studiare il segno del prodotto {(x-1)(x+1)}. Abbiamo:

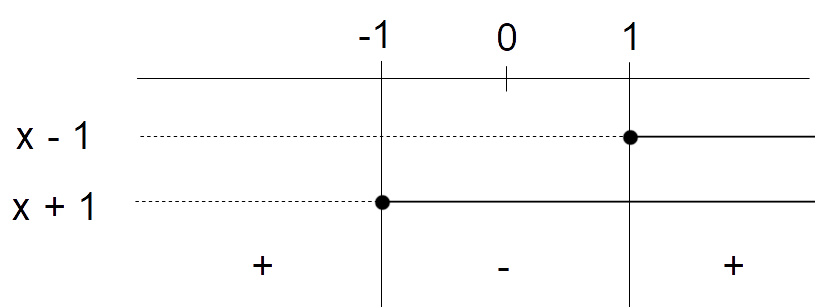
Così per la seconda condizione abbiamo:

x \leq -1 \quad \vee \quad x \geq 1

Così per le condizioni di esistenza dell’espressione con radicali di partenza dovranno valere contemporaneamente entrambe le condizioni di esistenza dei radicali presenti nell’espressione:

\begin{cases}x \geq -1 \\ \\  x \leq -1 \quad \vee \quad x \geq 1\end{cases}

Risolviamo graficamente il sistema intersecando gli insiemi delle {x} che soddisfano le due condizioni:

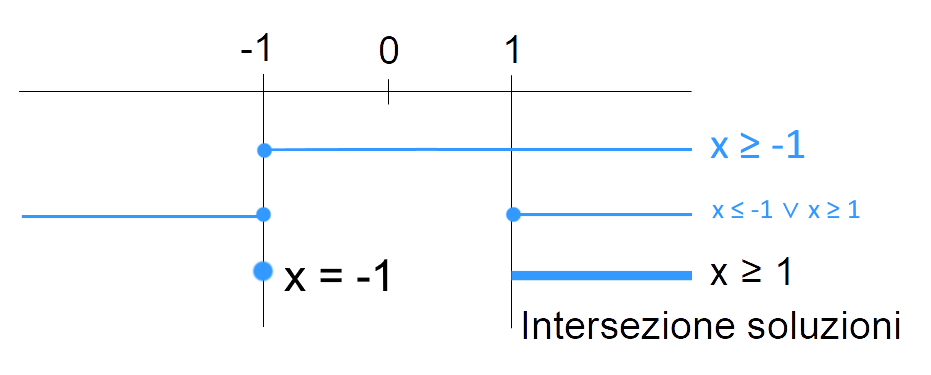
Otteniamo così in conclusione per l’espressione la condizione di esistenza:

\boxed{x = -1 \quad \vee \quad x \geq 1}

Esercizio 10

Concludiamo questa serie di esercizi sulle condizioni di esistenza dei radicali con la seguente espressione:

\dfrac{\sqrt{x^2+4}}{\sqrt{x}}+\sqrt{1-x}

Studiamo prima di tutto separatamente le condizioni di esistenza di ciascun radicale.

Tutti i radicali hanno indice pari e di conseguenza richiediamo intanto che il radicando sia non negativo per ciascuno di essi.

Per il radicale a numeratore della frazione, osserviamo che il suo radicando è sempre positivo. Quindi tale radicale esiste per ogni valore reale della {x}.

Per il radicale a denominatore della frazione, dovrà essere {x > 0}. Infatti, il radicando non può essere negativo e nemmeno nullo, poiché il radicale si trova al denominatore.

Infine, per il rimanente radicale {\sqrt{1-x}} abbiamo:

\sqrt{1-x}  \quad \text{esiste}\: \iff  1-x \geq 0 \iff x \leq 1

Per cui, dovendo valere contemporaneamente tutte le condizioni precedentemente scritte, le condizioni di esistenza dell’espressione di partenza sono:

x  > 0 \: \wedge x \neq 0 \: \wedge x \leq 1  

e quindi in conclusione:

0 < x  \leq 1

Conclusioni

Per quanto riguarda questa serie di esercizi sulle condizioni di esistenza dei radicali è tutto. Buon proseguimento con SìMatematica!