Esercizi sulla distanza tra due punti nel piano

 - 

Esercizi sulla retta nel piano e coordinate cartesiane

Proponiamo in questa scheda una serie di esercizi sul calcolo della distanza tra due punti nel piano cartesiano. Ricordiamo che, dati due punti {P_1=(x_1,y_1)} e {P_2=(x_2, y_2)} del piano, la formula generale per il calcolo della distanza {\overline{P_1P_2}} tra i due punti dati è:

\overline{P_1P_2}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

Nel caso in cui i due punti abbiano la stessa ascissa ({x_1=x_2}), la formula si riduce a:

\overline{P_1P_2}=|y_2-y_1|, \qquad x_1=x_2

mentre nel caso in cui abbiano la stessa ordinata ({y_1=y_2}) la formula diviene:

\overline{P_1P_2}=|x_2-x_1|, \qquad y_1=y_2

Infine, nel caso in cui uno dei due punti sia l’origine degli assi, il problema si riduce al calcolo della distanza di una dato punto {P=(x,y)} rispetto all’origine {O=(0,0)} degli assi:

\overline{OP}=\sqrt{x^2+y^2}, \qquad \text{distanza di un punto dall'origine}

Le ultime tre formule appena illustrare derivano immediatamente dalla formula generale, che è comunque applicabile in tutti i casi. Negli esercizi a seguire sul calcolo della distanza tra due punti nel piano, mostreremo l’utilizzo sia della formula generale, sia delle sue versioni più compatte, ove possibile.

In più, a conclusione della scheda mostreremo un utilizzo pratico della formula sul calcolo della distanza tra due punti nel piano, presentando degli esercizi ove è richiesto di calcolare il perimetro di figure geometriche.

Esercizi sul calcolo della distanza tra due punti nel piano

Prima parte: come utilizzare la formula della distanza tra due punti nel piano

Esercizio 1

Calcolare la distanza tra i due punti {P_1=(-2,3)} e {P_2=(4,3)}.

Cominciamo scrivendo le coordinate secondo le convenzioni adottate nella formula generale:

\begin{align*} &P_1=(-2,3)=(x_1,y_1) \quad \Rightarrow x_1=-2, \: y_1=3 \\ \\ &P_2=(4,3)=(x_2,y_2) \quad \Rightarrow x_2=4, \: y_2=3 \end{align*}

Ora, attenzione. Poiché abbiamo {y_1=y_2}, i due punti hanno la stessa ordinata e dunque possiamo utilizzare la formula per il calcolo della distanza tra due punti nell’opportuna forma compatta. Nel nostro caso abbiamo:

\overline{P_1P_2}=|x_2-x_1|=|4-(-2)|=|4+2|=|6|=6

Dal punto di vista grafico, osserviamo che la distanza calcolata corrisponde alla misura del segmento che unisce i due punti dati (vedi figura).

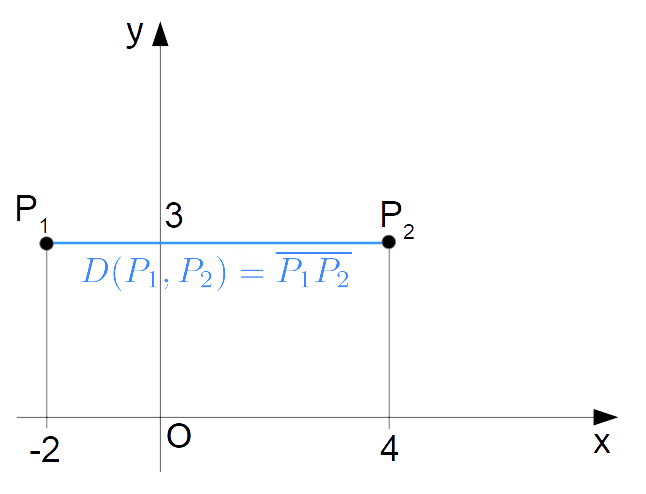
Importante. Prestiamo molta attenzione ai segni quando sostituiamo alle quantità letterali i corrispondenti valori numerici. Al fine di evitare errori, se si è ancora inesperti è sempre bene fare un abbondante uso delle parentesi tonde.
In particolare, è importante ricordare che in generale si ha {a-(-b)=a+b}. In questo modo sarà possibile prevenire spiacevoli errori di segno nel caso in cui le coordinate {x_1} e/o {y_1} siano negative.

Così in conclusione la distanza tra i due punti dati è {\overline{P_1P_2}=6}.

In alternativa avremmo anche potuto utilizzare la formula generale:

\begin{align*} & \overline{P_1P_2} = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{[4-(-2)]^2+(3-3)^2}= \\ \\ & =\sqrt{6^2+0^2}=\sqrt{36}=6\end{align*}

Pur con più calcoli perveniamo anche in questo modo al risultato finale.

Esercizio 2

Proseguiamo gli esercizi sul calcolo della distanza tra due punti del piano con il seguente, riguardante un caso ove è necessario applicare la formula generale.

Calcolare la distanza tra i due punti {P_1=(3,5)} e {P_2=(-6,-4)}.

Cominciamo prima di tutto scrivendo le coordinate:

\begin{align*} &P_1=(3,5)=(x_1,y_1) \quad \Rightarrow x_1=3, \: y_1=5\\ \\ & P_2=(-6,-4)=(x_2,y_2) \quad \Rightarrow x_2=-6,  \: y_2=-4\: \end{align*}

Non abbiamo nessuna uguaglianza né fra le ascisse né fra le ordinate, per cui in questo caso dobbiamo utilizzare esclusivamente la formula generale. Si ha:

\begin{align*} &\overline{P_1P_2}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} = \\ \\ & =\sqrt{(-6-3)^2+(-4-5)^2}=\sqrt{(-9)^2+(-9)^2}=\sqrt{81+81}=\\ \\ & =\sqrt{162}=\sqrt{2 \cdot 81} = \sqrt{2 \cdot 3^4}=3^2\sqrt{2}=9\sqrt{2}\end{align*}

Nel pervenire al risultato nella sua forma finale abbiamo fatto uso delle proprietà dei radicali. In particolare, abbiamo utilizzato le regole per semplificare i radicali.

Tra parentesi, se non si ricordano le regole sulla semplificazione dei radicali è comunque possibile cavarsela in questo caso ricordando in generale che {\sqrt{x}=x^{\frac{1}{2}}} (con {x \geq 0}) ed utilizzando le proprietà delle potenze:

\sqrt{2 \cdot 3^4} = \left( 2 \cdot 3^4\right)^{\frac{1}{2}}=2^{\frac{1}{2}}  \cdot  \left( 3^{4}\right)^{\frac{1}{2}}=\sqrt{2} \cdot 3^{4 \cdot \frac{1}{2}}=\sqrt{2} \cdot 3^2=3^2 \sqrt{2}=9\sqrt{2}

Nota: omettiamo per brevità negli esempi a seguire le rappresentazioni grafiche, che vi invitiamo comunque ad utilizzare.

Esercizio 3

Calcolare la distanza tra i due punti {P_1=(-5,0)} e {P_2=(-8,2)}.

Arrivati a questo punto possiamo sostituire direttamente i valori delle coordinate nella formula per il calcolo della distanza tra due punti nel piano. Ormai, grazie ai due precedenti esempi, il procedimento dovrebbe essere infatti chiaro.

\begin{align*} & \overline{P_1P_2}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} =\\ \\ & =\sqrt{[-8-(-5)]^2+(2-0)^2}=\sqrt{(-8+5)^2+2^2}=\\ \\ & =\sqrt{(-3)^2+4}=\sqrt{9+4}=\sqrt{13}\end{align*}

Esercizio 4

Proseguiamo gli esercizi sul calcolo della distanza tra due punti del piano proponendo ancora un esercizio con coordinate date da numeri interi relativi. A seguire ci occuperemo invece di punti aventi coordinate anche frazionarie.

Calcolare la distanza tra i due punti {P_1=(4, -2)} e {P_2=(-4,6)}.

Abbiamo:

\begin{align*} &{\overline{P_1P_2}}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} =\sqrt{(-4-4)^2+[6-(-2)]^2}=\\ \\ & =\sqrt{(-8)^2+(8^2)}=\sqrt{64+64}=\sqrt{128}=\sqrt{2^7}=\sqrt{2^6\cdot 2 } = \\ \\ & =2^3 \cdot \sqrt{2}=8\sqrt{2}\end{align*}

Esercizio 5

Calcolare la distanza tra i due punti del piano {P_1=\left(- \dfrac{1}{2}, -\dfrac{1}{2}\right)} e {P_2=(1,1)}.

Poiché ci ritroviamo con delle coordinate espresse con numeri frazionari, riportiamo a seguire i passaggi completi in modo da chiarire e/o ricordare come applicare le proprietà dei radicali e delle potenze al caso delle frazioni.

Abbiamo:

\begin{align*} &\overline{P_1P_2}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} =\\ \\ & =\sqrt{\left[ 1-\left( -\dfrac{1}{2}\right)\right]^2+\left[ 1-\left( -\dfrac{1}{2}\right)\right]^2}= \sqrt{\left( 1+\dfrac{1}{2}\right)^2+\left( 1+\dfrac{1}{2}\right)^2}=\\ \\ & =\sqrt{\left( \dfrac{3}{2}\right)^2+\left( \dfrac{3}{2}\right)^2}=\sqrt{\dfrac{9}{4}+\dfrac{9}{4}}=\sqrt{\dfrac{18}{4}} =\sqrt{\dfrac{3^2 \cdot 2}{2^2}}=\\ \\ & =\sqrt{\dfrac{1^2}{2^2} \cdot 3^2 \cdot 2}=\sqrt{\left( \dfrac{1}{2}\right)^2 \cdot3^2 \cdot 2} =\dfrac{1}{2} \cdot 3  \cdot \sqrt{2}=\dfrac{3}{2}\sqrt{2}\end{align*}

In particolare, ricordiamo che per elevare a potenza una frazione basta elevare a potenza sia il numeratore, sia il denominatore. La nuova frazione che così si ottiene è la potenza cercata.

Esercizio 6

Calcolare la distanza tra i due punti {P_1=\left( \dfrac{2}{5}, -\dfrac{1}{5}\right)} e {P_2= \left( -2, \dfrac{3}{5}\right)}.

Procediamo in maniera più spedita, dato che abbiamo mostrato i passaggi uno ad uno nell’esercizio precedente:

\begin{align*} &\overline{P_1P_2}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} =\\ \\ & =\sqrt{\left(-2-\dfrac{2}{5}\right)^2+\left[ \dfrac{3}{5}-\left( -\dfrac{1}{5}\right)\right]^2}=\\ \\ & =\sqrt{\left( -\dfrac{12}{5}\right)^2+\left( \dfrac{4}{5}\right)^2}=\sqrt{\dfrac{144}{25}+\dfrac{16}{25}}=\sqrt{\dfrac{160}{25}}=\\ \\ & =\sqrt{\dfrac{5 \cdot 2 \cdot 2^4}{5^2}}=\dfrac{4}{5}\sqrt{10}\end{align*}

Seconda parte: calcolo del perimetro di triangoli

A conclusione di questa serie di esercizi sul calcolo della distanza tra due punti del piano, proponiamo un paio di problemi relativi al calcolo del perimetro di triangoli.

Esercizio 7

Calcolare il perimetro del triangolo di vertici {A=(3,-5), \: B=(3,4), \: C=(-1, 7)}.

L’idea è quella di calcolare la distanza tra ciascuna coppia di vertici del triangolo utilizzando la formula per la distanza tra due punti del piano. In tal modo si ottiene la misura di ciascun lato del triangolo. Infine, sommando tali misure tra loro si ottiene il perimetro della figura.

Il primo passo è dunque dato dal calcolo delle distanze {\overline{AB}}, {\overline{BC}} e {\overline{AC}}, in modo da avere le misure dei lati del triangolo.

Indichiamo le coordinate dei punti dati come:

\small A=(3,-5)=(x_A, y_A); \quad B=(3,4)=(x_B,y_B); \quad C=(-1,7)=(x_C,y_C)

Abbiamo:

\begin{align*} &\overline{AB}=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{(3-3)^2+[4-(-5)]^2}=\\ \\ & =\sqrt{0+9^2}=\sqrt{81}=9; \\ \\ &\overline{BC} = \sqrt{(x_C-x_B)^2+(y_C-y_B)^2}=\sqrt{(-1-3)^2+(7-4)^2}=\\ \\ & =\sqrt{(-4)^2+3^2}=\sqrt{16+9}=\sqrt{25}=5;\\ \\ & \overline{AC}=\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}=\sqrt{(-1-3)^2+[7-(-5)]^2}=\\ \\ & =\sqrt{(-4)^2+12^2}=\sqrt{16+144}=\sqrt{160}=\sqrt{2^4 \cdot 5 \cdot 2}=4\sqrt{10}\end{align*}

Ora non resta che calcolare il perimetro, sommando tra loro le misure dei lati:

p=\overline{AB}+\overline{BC}+\overline{AC}=9+5+4\sqrt{10}=14+4\sqrt{10}=2\left(7+2\sqrt{10}\right)

Osservazione. Nel calcolare la distanza {\overline{AB}} avremmo anche potuto applicare la formula nella opportuna versione più compatta:{\overline{AB}=|y_B-y_A|=|4-(-5)|=9}Ciò si giustifica osservando che i punti {A} e {B} condividono la stessa ascissa ({x_A=x_B}).

Esercizio 8

Calcolare il perimetro del triangolo di vertici {A=\left( 0, -\dfrac{1}{2}\right), \: B=\left( -5, \dfrac{3}{2}\right), \: C=\left( 8, \dfrac{1}{2}\right)}.

Procediamo né più né meno che come nell’esercizio precedente. Vi invitiamo a svolgere da soli l’esercizio, per poi verificare il vostro procedimento con quello qui proposto.

\begin{align*} &\overline{AB}=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{(-5-0)^2+\left[ \dfrac{3}{2}-\left( -\dfrac{1}{2}\right)\right]^2}=\\ \\ & =\sqrt{25+4}=\sqrt{29}; \\ \\ & \overline{BC}=\sqrt{(x_C-x_B)^2+(y_C-y_B)^2}=\sqrt{[8-(-5)]^2+\left( \dfrac{1}{2}-\dfrac{3}{2}\right)^2}=\\ \\ & =\sqrt{169+1}=\sqrt{170}; \\ \\ & \overline{AC}=\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}=\sqrt{(8-0)^2+\left[ \dfrac{1}{2}-\left( -\dfrac{1}{2}\right)\right]^2}=\\ \\ & =\sqrt{64+1}=\sqrt{65}; \\ \\ &p = \overline{AB}+\overline{BC}+\overline{AC}=\sqrt{29}+\sqrt{170}+\sqrt{65};\end{align*}

Per questa scheda di esercizi sulla formula relativa al calcolo della distanza tra due punti nel piano è tutto. Buon proseguimento con SìMatematica!