Fascio di rette

 - 

Coordinate cartesiane e retta nel piano

Un fascio di rette è una famiglia di rette tali da passare tutte per uno stesso punto (fascio proprio di rette) o tali da essere tutte parallele tra loro (fascio improprio di rette).

Il punto di partenza per la definizione di fascio proprio di rette è dato dalla equazione di una retta del piano cartesiano nelle forme esplicita o implicita. In particolare, al variare di un opportuno parametro reale sarà possibile ottenere ciascuna delle rette appartenenti al fascio. Come vedremo, infatti, per ogni valore di un certo parametro reale si ottiene l’equazione di una delle infinite rette del fascio.

Nel caso dell’equazione di una retta in forma esplicita, l’idea alla base della nozione di fascio proprio di rette è quella di partire dall’equazione di una retta del piano noti un punto e la sua pendenza, e quindi esprimere il coefficiente angolare come funzione di un opportuno parametro reale. Tale approccio, come anticipato, può essere utilizzato anche nel caso dell’equazione di una retta in forma implicita, ma in tale circostanza il discorso si complica leggermente.

Infine, per quanto riguarda la definizione di fascio improprio di rette, l’idea è quella di ottenere, anche in questo caso in funzione di un opportuno parametro reale, tutte le rette parallele ad una certa retta di partenza.

Fascio proprio di rette (forma esplicita)

Dati due punti del piano cartesiano, la retta passante per i due punti è unica. Lo stesso però non può dirsi nel caso di un solo punto. Infatti, per un punto del piano passano infinite rette.

Così, dato un punto {C(x_0, y_0)} del piano cartesiano, l’equazione in forma esplicita di una retta passante per esso è data da:

y-y_0=m(x-x_0)

ove il coefficiente angolare {m} è un numero reale finito. Tuttavia, se sostituiamo al coefficiente angolare {m} una opportuna funzione, ciò che otteniamo è l’equazione di un fascio proprio di rette. E poiché l’equazione della retta dalla quale partiamo è in forma esplicita, anche il fascio sarà scritto in forma esplicita.

In particolare, ponendo {m=m(k)}, ovvero sostituendo nella precedente equazione al posto del coefficiente angolare una opportuna funzione del parametro reale {k}, otteniamo:

y-y_0=m(k) (x-x_0), \qquad k \in \R

la quale rappresenta il fascio proprio di rette (in forma esplicita) centrato nel punto {C=(x_0, y_0)}. In altre parole, l’equazione appena scritta rappresenta tutte le possibili rette del piano tali da passare per il punto {C=(x_0, y_0)} (ad eccezione della retta verticale passante per {C}, in quanto per essa il coefficiente angolare non è definito).

I valori {x_0} ed {y_0} sono fissati e rappresentano le coordinate del punto {C}. Invece, il coefficiente angolare è variabile e cambia in funzione del parametro reale {k}. In altre parole, ad ogni valore del parametro {k} corrisponde uno ed un solo valore del coefficiente angolare {m}. Di conseguenza, al variare di {k} in {\R} otterremo rette con tutte le possibili pendenze (esclusa la retta verticale) e tali che il punto {C(x_0, y_0)} sia appartenente a ciascuna di esse.

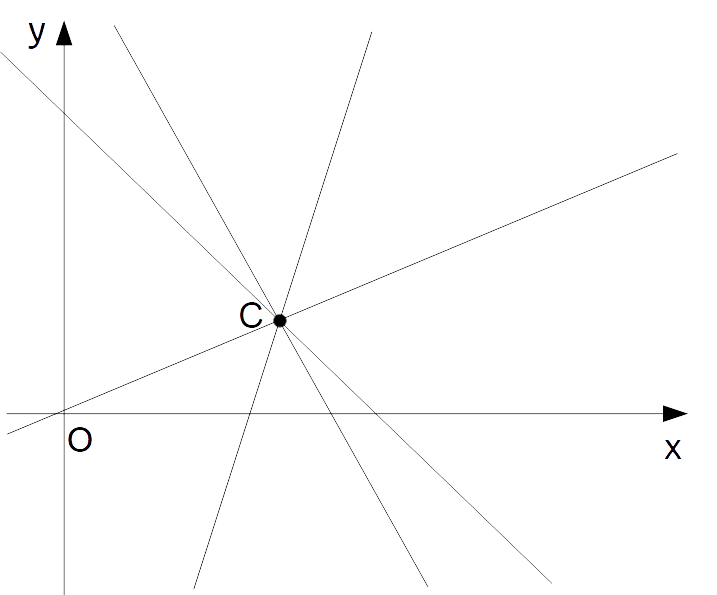
La retta verticale passante per il punto {C} è esclusa dall’insieme delle rette del fascio di equazione in forma esplicita poiché per le rette verticali il coefficiente angolare {m} non è definito.

Esempi sui fasci propri di rette in forma esplicita

Esempio 1

Scrivere l’equazione del fascio proprio di rette con centro {C=(2, 5)}.

Abbiamo:

y-y_0 = m(k) (x-x_0) \quad \Rightarrow \quad y-5=m(k)(x-2)

L’equazione rappresenta l’insieme di tutte le rette del piano cartesiano tali da passare per il punto {C=(2,5)} (esclusa la retta verticale).

Esempio 2

Determinare il centro del fascio proprio di equazione {y-4=m(k)(x+3)}.

Ricordiamo che la forma generica dell’equazione di un fascio proprio di rette passanti per un punto {C=(x_0, y_0)} (forma esplicita) è:

y-y_0=m(k)(x-x_0)

Nel nostro caso abbiamo {x_0=-3} (attenzione al segno) e {y_0=4}. Infatti, sostituendo nella precedente ritroviamo l’equazione del fascio data in partenza:

y-4=m(k)[x-(-3)] \quad \Rightarrow \quad y-4=m(k)(x+3)

Così il punto {C=(-3, 4)} è il centro del fascio proprio di rette dato.

Non sempre è possibile studiare i fasci di rette nel modo agevole che abbiamo visto negli esempi sinora presentati. Immediatamente a seguire proporremo dunque un’ulteriore forma dell’equazione di un fascio proprio di rette, che consentirà lo studio dei fasci di rette anche nei casi più generali.

Fascio proprio di rette in forma implicita

Leggermente più complicato è il caso del fascio proprio di rette con equazione data in forma implicita. Partiamo dall’equazione di una retta del piano in forma implicita:

r: ax+by+c=0, \qquad a,b,c \in \R

con {a} e {b} mai contemporaneamente nulli.

Dato un punto {C=(x_0, y_0)}, vogliamo scrivere l’equazione in forma implicita di una retta che passi per esso. A tale scopo, dobbiamo prima di tutto imporre la condizione di appartenenza del punto alla retta. Questa si ottiene sostituendo nell’equazione della retta {r} le coordinate del punto dato:

ax_0+by_0+c=0

da cui ricaviamo il valore del termine noto {c} corrispondente ad una retta passante per il punto {C}:

c=-ax_0-by_0

Così, sostituendo al termine noto {c} nell’equazione della retta {r} l’espressione appena ottenuta abbiamo:

ax+by-ax_0-by_0=0

Questa è l’equazione di una retta passante per il punto {C=(x_0, y_0)}. Inoltre, raccogliendo i coefficienti {a} e {b} al primo membro:

a(x-x_0)+b(y-y_0)=0

Se ora sostituiamo ai coefficienti {a} e {b} delle opportune funzioni di un parametro reale {k}, otteniamo l’equazione:

a(k)(x-x_0)+b(k)(y-y_0)=0

la quale rappresenta l’equazione in forma implicita del fascio proprio di rette avente come centro il punto {C=(x_0, y_0)}.

Tuttavia, per questioni formali si preferisce spesso scrivere l’equazione in forma implicita di un fascio di rette in altro modo. Ciò consente, tra l’altro, di poter studiare i fasci di rette anche nei casi più generali.

A seguire proponiamo un metodo, non perfettamente rigoroso ma accettabile in questo contesto, per ricavare l’equazione in forma implicita di un fascio, in una variante particolarmente utile per gli esercizi. Chi non desidera seguire tutti i passaggi può comunque saltare direttamente alla definizione.

Consideriamo in particolare due rette {r_1} ed {r_2} del piano, di equazioni:

r_1 :a_1x+b_1y+c_1=0, \qquad r_2:a_2x+b_2y+c_2=0

e tali da passare entrambe per un dato punto {C=(x_0, y_0)}.

Poiché il punto {C} appartiene ad entrambe le rette, dovranno valere contemporaneamente le seguenti condizioni di appartenenza:

a_1x_0+b_1y_0+c_1=0, \qquad a_2x_0+b_2y_0+c_2=0

dalle quali si ottiene, rispettivamente:

c_1=-a_1x_0-b_1y_0, \qquad c_2=-a_2x_0-b_2y_0 \qquad (@)

Questi sono i valori dei termini noti che fanno sì che le rette {r_1} ed {r_2} siano entrambe passanti per {C}.

Ora, indicati con {t} e {h} due parametri reali, a partire dalle equazioni delle rette {r_1} ed {r_2} possiamo costruire la seguente equazione:

t(a_1x+b_1y+c_1)+h(a_2x+b_2y+c_2)=0 \qquad (@@)

Come possiamo vedere, all’interno delle parentesi tonde figurano i primi membri delle equazioni di {r_1} ed {r_2}. Una tale rappresentazione si dice combinazione lineare delle due equazioni di partenza.

E’ importante osservare che poiché le rette {r_1} ed {r_2} si intersecano nel punto {C}, al variare dei parametri {t} e {h} in tutto l’insieme dei numeri reali l’equazione @@ risulterà sempre verificata in corrispondenza del punto {C}. Inoltre, se sommiamo membro a membro tra loro due equazioni relative a delle rette, ciò che otteniamo è ancora l’equazione di una retta. Così, al variare dei parametri {t} e {h} otterremo rette di varie pendenze ma comunque sempre passanti per {C}. A ciò corrisponde un fascio di rette proprio con centro in {C}.

Ora, supponendo {t \neq 0}, dividendo opportunamente per {t} possiamo scrivere:

a_1x+b_1y+c_1+\dfrac{h}{t}(a_2x+b_2y+c_2)=0

e ponendo per semplicità {\dfrac{h}{t}=k, k \in \R} otteniamo in conclusione:

\boxed{a_1x+b_1y+c_1+k(a_2x+b_2y+c_2)=0, \qquad k \in \R} \quad (**)

ovvero la forma più comune per scrivere l’equazione di un fascio proprio di rette con centro nel punto di intersezione tra le due rette {r_1 : a_1x+b_1y+c_1} e {r_2:a_2x + b_2y+c_2}.

Le rette {r_1} ed {r_2} si dicono rette generatrici del fascio. E la retta la cui equazione è moltiplicata per il parametro {k} si dice retta esclusa. Infatti, dall’equazione del fascio non otteniamo l’equazione della retta {r_2} per nessun valore reale del parametro {k}. E’ invece immediato verificare che è possibile ricondursi all’equazione della retta {r_1} per {k=0}.

Osservazione. Torniamo indietro all’equazione: {t(a_1x+b_1y+c_1)+h(a_2x+b_2y+c_2)=0, \quad t,h \in \R}Tale equazione consente di ottenere la retta di equazione {a_2x+b_2y+c_2=0} semplicemente ponendo {t=0} e {h=1}. Ricordiamo tuttavia che per ottenere la ** abbiamo posto la condizione {t \neq 0}. Ciò significa che per nessun valore del parametro {k} è possibile ottenere la retta di equazione {a_2x+b_2y+c_2=0}, che rappresenta effettivamente la retta esclusa dal fascio.

Definizione (fascio proprio di rette in forma implicita). Dato un punto {C=(x_0, y_0)}, una famiglia di rette passanti per tale punto è descritta dall’equazione:{\boxed{a_1x+b_1y+c_1+k(a_2x+b_2y+c_2)=0, \qquad k \in \R} \quad (**)}che rappresenta un fascio proprio di rette in forma implicita. Nel primo membro è possibile individuare le equazioni corrispondenti a due rette {r_1} ed {r_2}:{r_1:a_1x+b_1y+c_1=0, \qquad r_2:a_2x+b_2y+c_2=0} Tali rette si dicono rette generatrici del fascio, e la retta {r_2} è detta retta esclusa, poiché non è effettivamente possibile ricondursi alla sua equazione a partire dall’equazione del fascio per nessun valore reale del parametro {k}.

L’equazione nella forma (**) è importante poiché consente di studiare agevolmente un fascio di rette, ovvero classificarlo a partire dalla sua equazione, data in qualunque forma.

Come studiare un fascio proprio di rette nel caso più generale

Data un’equazione di primo grado nelle variabili {x} e {y}, contenente un parametro {k} reale, ovvero un’equazione di primo grado del tipo {f(x,y,k)=0}, il nostro obiettivo è stabilire se si tratta di una fascio proprio di rette o meno e nel caso determinare le coordinate {x_0} ed {y_0} del punto centro del fascio.

L’idea è quella di ricondurre l’equazione data alla forma **, per poi intersecare tra loro le rette generatrici. L’eventuale punto di intersezione così ottenuto sarà il centro del fascio. Si tratterà quindi di risolvere il sistema lineare contenente le equazioni delle rette generatrici del fascio.

Se il sistema lineare risulta determinato, l’equazione di partenza effettivamente rappresenta un fascio proprio di rette.

Se invece il sistema risulta indeterminato o impossibile, l’equazione rappresenta rispettivamente un fascio degenere (ovvero un fascio che per ogni valore del parametro reale {k} restituisce sempre la medesima retta) oppure, come vedremo più avanti, un fascio improprio (ovvero una famiglia di rette tutte parallele tra loro).

Esempio (studio di un fascio proprio di rette)

Stabilire se l’equazione {(2 + 2k)x + (3 − k)y − 8k = 0} rappresenta un fascio proprio di rette, e nel caso determinare le coordinate del punto centro del fascio.

Cerchiamo prima di tutto di ricondurre l’equazione data alla forma **. Cominciamo eseguendo le moltiplicazioni al primo membro:

\small(2 + 2k)x + (3 − k)y − 8k = 0 \quad \Rightarrow \quad 2x+2kx+3y-ky-8k=0

Fatto ciò, ordiniamo opportunamente i termini in modo da raggruppare tra loro i termini che non contengono il parametro {k} e quelli che lo contengono:

2x+3y+2kx-ky-8k=0

Infine raccogliamo parzialmente per {k}:

2x+3y+0+k(2x-y-8)=0

Abbiamo così ricondotto l’equazione alla forma **. In particolare, ci ritroviamo con una forma del tipo {a_1x+b_1y+c_1+k(a_2x+b_2y+c_2)=0}, con {a_1=2, b_1 = 3, c_1 = 0, a_2 = 2, b_2 = -1, c_2 = -8}.

La rette generatrici del fascio sono:

r_1: 2x+3y=0, \qquad r_2:2x-y-8=0

ove {r_2} è la retta esclusa.

A questo punto, per determinare le coordinate del centro del fascio dobbiamo determinare (se esiste) il punto di intersezione tra le rette {r_1} ed {r_2}. Si tratta quindi di risolvere il sistema lineare contenente le equazioni delle due rette, ovvero:

\begin{cases} 2x+3y=0 \\ \\ 2x-y-8=0\end{cases}

Risolvendo il sistema ad esempio per riduzione abbiamo:

\begin{cases} 4y+8=0 \quad \rightarrow \quad y=-2 \\ \\ 2x-y-8=0 \quad \rightarrow \quad x=3\end{cases}

Poiché il sistema è determinato, siamo in presenza in conclusione di un fascio proprio di rette, con rette generatrici {r_1} ed {r_2} e centro {C=(3,-2)}.

Fascio improprio di rette

Un fascio improprio di rette è costituito da una famiglia di rette tutte parallele tra loro. Le rette non presentano nessun punto in comune, nemmeno prese a due a due.

Per quanto sappiamo sulla condizione di parallelismo tra rette, se le rette del fascio sono parallele tra loro queste hanno lo stesso coefficiente angolare. Ciò che cambia è invece l’ordinata all’origine, che in una fascio improprio di rette è infatti funzione di un parametro reale {k}.

Così, a partire dall’equazione in forma esplicita di una retta del piano cartesiano:

y=mx+q

l’idea è quella di mantenere fisso il coefficiente angolare {m}, esprimendo invece l’ordinata all’origine {q} come funzione del parametro reale {k}:

y=mx+q(k), \qquad k \in \R

e questa è l’equazione di un fascio improprio di rette aventi tutte lo stesso coefficiente angolare {m}.

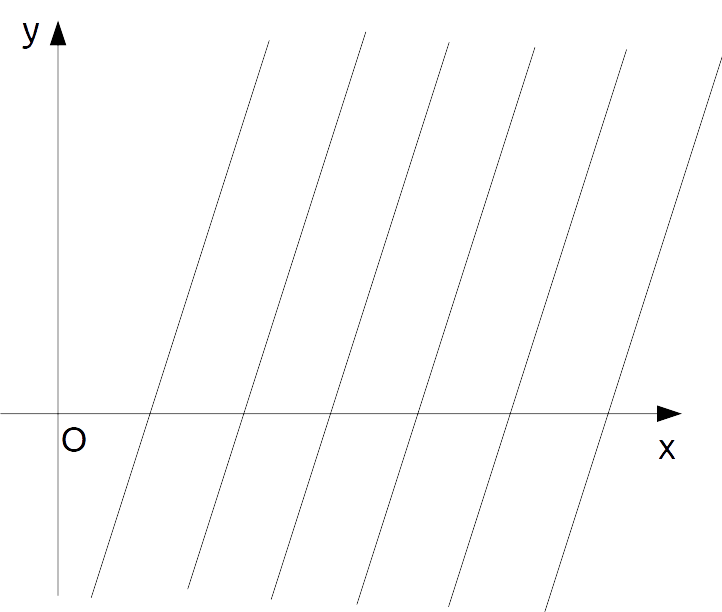
La rappresentazione in forma implicita di un fascio improprio è del tutto simile a quella già vista per un fascio di rette proprio. Ciò non è comunque fonte di confusione, in quanto è sempre possibile riconoscere se un fascio è improprio mettendo a sistema le rette generatrici. Se il sistema è impossibile, le rette non presentano alcun punto di intersezione e di conseguenza abbiamo un fascio di rette improprio. Ma passiamo subito ad un esempio.

Esempio (fascio improprio)

Verificare che il fascio di equazione {(1 − k)x − 2(1 − k)y + 3 = 0} è un fascio improprio.

Riconduciamo prima di tutto l’equazione del fascio alla forma:

a_1x+b_1y+c_1+k(a_2x+b_2y+c_2)=0

Per fare questo, eseguiamo prima di tutto i prodotti al primo membro, per poi raggruppare tra loro i termini che non contengono il parametro {k} e quelli che invece lo contengono:

\begin{align*} &(1 − k)x − 2(1 − k)y + 3 = 0; \\ \\ & x-kx-2y+2ky+3=0; \\ \\ &x-2y+3-kx+2ky=0\end{align*}

Concludiamo eseguendo un raccoglimento parziale per il parametro {k}:

x-2y+3+k(-x+2y)=0

Abbiamo così ricondotto l’equazione alla forma desiderata. Riconosciamo in essa le due rette generatrici:

r_1: x-2y+3=0, \qquad r_2: -x+2y=0

Impostiamo il sistema lineare che ci consentirà di stabilire se esiste o meno un punto di intersezione tra le due rette:

\begin{cases} x-2y+3=0 \\ \\ -x+2y=0\end{cases}

Risolvendo il sistema ad esempio per riduzione abbiamo:

\begin{cases} 3= 0 \\ \\ -x+2y=0\end{cases}

Ci ritroviamo con un’equazione numerica falsa (prima equazione a sistema), e di conseguenza il sistema è impossibile. Ciò significa che le rette non presentano un punto di intersezione, e pertanto il fascio è improprio.

Un ulteriore esempio su come classificare un fascio di rette

Vediamo un ulteriore esempio su come classificare un fascio di rette a partire dalla sua equazione, data nella forma {f(x,y,k)=0}, di primo grado. Ci concentreremo per ora sui soli due casi di fasci propri o impropri, rimandando all’ultima parte della lezione il caso dei fasci degeneri.

Data l’equazione {(k-1)x+(2k+3)y-k+7=0}, stabilire se questa rappresenta un fascio proprio o improprio. Determinare inoltre le equazioni delle rette generatrici e scrivere l’equazione della retta del fascio passante per il punto {P=(-1,1)}.

Cominciamo calcolando tutti i prodotti al primo membro dell’equazione:

\begin{align*} & (k-1)x+(2k+3)y-k+7=0;\\ \\ & kx-x+2ky+3y-k+7=0\end{align*}

Proseguiamo separando i termini che non contengono il parametro {k} da quelli che lo contengono:

-x+3y+7+kx+2ky-k=0

Raccogliamo parzialmente per {k}:

-x+3y+7+k(x+2y-1)=0

Siamo già in grado di scrivere le equazioni delle rette generatrici. Infatti, l’equazione è ora della forma **. Per cui abbiamo:

r_1:-x+3y+7=0, \qquad r_2: x+2y-1=0

ove {r_2} è la retta esclusa.

Ora, se il fascio è proprio il sistema lineare dato dalle equazioni di {r_1} ed {r_2} dovrà essere determinato. Proviamo a risolverlo:

\begin{cases} -x+3y+7=0 \\ \\ x+2y-1=0\end{cases}

Procedendo per riduzione abbiamo:

\begin{cases} 5y+6=0 \quad \rightarrow \quad y=-\dfrac{6}{5}\\ \\ x=\dfrac{12}{5}+1=\dfrac{17}{5}\end{cases}

Di conseguenza il fascio è proprio ed ha centro {C=\left( \dfrac{17}{5}, -\dfrac{6}{5}\right)}.

Rimane infine da scrivere l’equazione della retta del fascio passante per il punto {P=(-1,1)}.

Poiché per ipotesi la retta appartiene al fascio, questa dovrà anche passare per il punto {C=\left( \dfrac{17}{5}, -\dfrac{6}{5}\right)}, che è il centro del fascio. Così, basterà utilizzare l’equazione di una retta passante per due punti:

\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}

ovvero nel nostro caso, ponendo ad esempio {C=\left( \dfrac{17}{5}, -\dfrac{6}{5}\right)=(x_1, y_1)} e {P=(-1,1)=(x_2, y_2)}:

\dfrac{y+\dfrac{6}{5}}{1+\dfrac{6}{5}}=\dfrac{x-\dfrac{17}{5}}{-1-\dfrac{17}{5}}

ovvero:

\begin{align*} &\dfrac{\dfrac{5y+6}{5}}{\dfrac{11}{5}}=\dfrac{\dfrac{5x-17}{5}}{\dfrac{-22}{5}}; \\ \\ & \dfrac{5y+6}{5} \cdot \dfrac{5}{11}=\dfrac{5x-17}{5} \cdot \dfrac{5}{-22}; \\ \\ &\dfrac{5y+6}{11}=\dfrac{17-5x}{22}; \\ \\ &\dfrac{5y+6}{11}-\dfrac{17-5x}{22}=0; \\ \\& \dfrac{10y+12-17+5x}{\cancel{22}}=0; \\ \\ & 5x+10y-5=0; \\ \\ & x+2y-1=0\end{align*}

Così la retta {s} del fascio passante per il punto {P=(-1,1)} avrebbe equazione:

s:x+2y-1=0

ma tale equazione è equivalente all’equazione della retta esclusa (le due equazioni sono date da uno stesso polinomio uguagliato a zero). Di conseguenza, non esiste alcuna retta del fascio tale da passare per il punto {P=(-1,1)}.

Importante. Nel verificare se esiste o meno una retta del fascio tale da passare per un assegnato punto {P}, se utilizziamo la formula della retta passante per due punti, come appena mostrato, dobbiamo sempre confrontare l’equazione che otteniamo con l’equazione della retta esclusa. Se le due equazioni sono equivalenti, e quindi le due rette coincidono, allora non esiste alcuna retta del fascio tale da passare per il punto assegnato. Diversamente, se le due equazioni non sono equivalenti, l’equazione ottenuta corrisponde proprio alla retta del fascio tale da passare per il punto dato.
Per stabilire se le due equazioni sono equivalenti o meno, basta ridurle entrambe alla forma {P(x,y)=0}, facendo in modo che ad esempio i termini in {x} di ciascuna equazione siano tra loro uguali. Se i due polinomi al primo membro sono uguali, le due equazioni sono equivalenti. Se questi sono diversi, le equazioni non sono equivalenti. Vedremo questa tecnica in azione nell’esercitazione correlata, che potete trovare nel link in fondo a questa lezione.

In alternativa al metodo presentato, per determinare se esiste una retta del fascio passante per il punto {P=(-1,1)} possiamo anche verificare se, partendo dall’equazione del fascio, riusciamo a determinare un valore del parametro {k} corrispondente alle coordinate del punto {P}. Ciò significa in altre parole ricercare un valore del parametro {k} tale da ridurre l’equazione del fascio all’equazione di una retta passante per il punto {P}.

Partiamo quindi dall’equazione del fascio (preferibilmente nella forma **):

-x+3y+7+k(x+2y-1)=0

Sostituiamo alle variabili {x} e {y} rispettivamente le coordinate {x_0} e {y_0} del punto {P}:

1+3+7+k(-1+2-1)=0 \quad \Rightarrow \quad11=0

Effettivamente otteniamo un’identità numerica falsa (quindi un assurdo), e di conseguenza non esiste alcun valore del parametro {k} corrispondente ad una retta del fascio passante per il punto {P}. Quindi, in conclusione, ritroviamo anche in questo modo il risultato che non esiste alcuna retta del fascio passante per il punto {P=(-1,1)}.

Fascio di rette degenere

A conclusione della lezione mostriamo un esempio relativo ad un fascio di rette degenere. Come già anticipato, un fascio di rette è degenere se il sistema contenente le equazioni delle rette generatrici del fascio è indeterminato. In tal caso, per ogni valore del parametro {k} otteniamo un’equazione relativa sempre alla stessa retta.

Classificare il fascio avente le rette generatrici {r_1:x+3y-1=0} e {r_2:2x+6y-2=0}.

Mettiamo le equazioni delle rette generatrici a sistema:

\begin{cases} x+3y-1=0 \\ \\ 2x+6y-2=0\end{cases}

Risolvendo il sistema per riduzione otteniamo:

\begin{cases} 2x+6y-2=0 \\ \\ 2x+6y-2=0 \end{cases} \quad \Rightarrow \quad \begin{cases} 0=0 \\ \\ 2x+6y-2=0\end{cases}

Data la presenza dell’uguaglianza {0=0}, che è un’identità, il sistema è indeterminato. Di conseguenza, le due rette generatrici hanno infiniti punti di intersezione e sono coincidenti. Per cui il fascio di rette è degenere. Ed in parole povere, ciò significa a lato pratico che il fascio di rette dato si riduce in questo caso ad una retta del piano.

Conclusioni

Per quanto riguarda i fasci di rette propri, impropri e degeneri è tutto. Con questa lezione si conclude anche il corso di lezioni di SìMatematica dedicato alle rette del piano cartesiano. A partire dalla prossima lezione ci occuperemo delle parabole. Buon proseguimento ed un saluto a tutti voi!