Proponiamo in questa scheda una serie di esercizi svolti sui fasci di rette, nei vari casi di fascio proprio, improprio e degenere. Sarà frequente l’uso della seguente rappresentazione implicita di un fascio:
a_1x+b_1y+c_1+k\left( a_2x+b_2y+c_2\right)=0, \quad k \in \R
ove compaiono le equazioni della retta {r_1}:
r_1: a_1x+b_1y+c_1=0
e della retta {r_2}, detta retta esclusa:
r_2: a_2x+b_2y+c_2=0
Tale retta è detta “esclusa” poiché effettivamente non è possibile ottenere la sua equazione, a partire dal fascio dato, per nessun valore del parametro reale {k}.
Ricordiamo inoltre che un fascio è proprio se l’intersezione tra le rette {r_1} ed {r_2} ha come risultato un punto del piano. In tal caso, tutte le rette del fascio hanno un solo punto in comune tra loro, detto centro del fascio.
Diversamente, un fascio è improprio se mettendo a sistema le equazioni delle rette {r_1} ed {r_2} ci ritroviamo un sistema impossibile. In questo caso le rette del fascio non hanno nessun punto in comune e sono di conseguenza tutte parallele tra loro.
Infine, un fascio di rette è degenere se mettendo a sistema le equazioni delle rette {r_1} ed {r_2} ci ritroviamo con un sistema indeterminato. In questo caso le rette del fascio hanno tutti i rispettivi punti in comune tra loro e di conseguenza il fascio si riduce ad una retta del piano.
Negli esercizi sui fasci di rette a seguire non ci limiteremo soltanto a classificare i fasci, ma risolveremo dei quesiti che interesseranno anche le precedenti lezioni sulla retta. Laddove necessario, effettueremo dei richiami teorici e rimanderemo alla lezione specifica per poter ripassare. Qui in particolare non proporremo esercizi di livello facile, poiché questi sono già stati presentati nell’ambito della lezione teorica sui fasci di rette. Di conseguenza, a chi non ha familiarità con i fasci di rette consigliamo vivamente di leggere prima tale lezione.
In particolare, negli esercizi sui fasci di rette di questa scheda mostreremo:
- come classificare un fascio e come determinare le equazioni delle sue rette generatrici;
- come determinare le equazioni delle rette del fascio che hanno una certa distanza rispetto ad un punto assegnato;
- ancora, come capire se una retta di equazione nota appartiene o meno ad un fascio dato;
- come determinare le equazioni delle rette del fascio parallele o perpendicolari ad una retta assegnata;
- come scrivere le equazioni delle rette del fascio che staccano/individuano un segmento di lunghezza nota su di un dato asse cartesiano;
- inoltre, come scrivere le equazioni delle bisettrici dell’angolo individuato da due particolari rette di un fascio;
- infine, come calcolare le coordinate del simmetrico di un dato punto rispetto ad una retta del fascio.
Fatti i dovuti richiami, cominciamo subito questa serie di esercizi sui fasci di rette, svolti e commentati.
Esercizi svolti e commentati sui fasci di rette (propri, impropri e degeneri)
Tracce tratte dall’inserto “La retta” del libro “Corso di Matematica”, risalente ai primi anni ’90.
Esercizio 1
Classificare il fascio di rette di equazione {(2+k)x+(1-2k)y+3k=0}, con {k} parametro reale, ed eventualmente determinare il centro del fascio, la retta del fascio perpendicolare alla bisettrice del primo e del terzo quadrante, ed infine scrivere le equazioni delle rette del fascio tali da distare {\dfrac{1}{5}} dal punto {A=(1,1)}.
Cominciamo con lo stabilire se il fascio è proprio, improprio o degenere. In altre parole, il primo passo consiste nel classificare il fascio.
Cerchiamo di ricondurre l’equazione del fascio alla forma:
a_1x+b_1y+c_1+k\left( a_2x+b_2y+c_2\right)=0
L’equazione del fascio data è:
(2+k)x+(1-2k)y+3k=0
Per ricondurla alla forma desiderata, prima di tutto eseguiamo le moltiplicazioni al primo membro:
2x+kx+y-2ky+3k=0
Ora riordiniamo i termini al primo membro, in modo da scrivere uno di seguito all’altro prima tutti i termini privi della lettera {k}, poi tutti i termini contenenti la lettera {k}:
2x+y+kx-2ky+3k=0
Infine, raccogliamo parzialmente per {k}:
2x+y+k(x-2y+3)=0
Ora il fascio è della forma desiderata, e riconosciamo in particolare le rette di equazione:
r_1:2x+y=0, \qquad r_2:x-2y+3=0
ove {r_2} è la retta esclusa. Utilizzeremo sempre questo stesso approccio per la determinazione delle rette generatrici in tutti gli esercizi sui fasci di rette di questa scheda.
A questo punto, intersechiamo le due rette tra loro, mettendo a sistema le rispettive equazioni (vedi: intersezione tra due rette). Se risolvendo il sistema otteniamo un valore per ciascuna incognita (sistema determinato), allora le due rette hanno un punto di intersezione. Di conseguenza, il fascio sarà proprio. Procediamo e vediamo cosa succede:
\begin{cases} 2x+y=0 \\ \\ x-2y+3=0\end{cases}Risolviamo il sistema per riduzione:
\small \begin{cases} 2x+y = 0 \\ \\ 2x-4y+6=0\end{cases} \quad \Rightarrow \quad \begin{cases} 5y-6=0 \quad \rightarrow \quad y=\dfrac{6}{5}\\ \\ 2x-4y+6=0 \quad \rightarrow \quad x=-\dfrac{3}{5}\end{cases}Il sistema è determinato e quindi il fascio dato è proprio. Il centro del fascio è:
C=\left( -\dfrac{3}{5}, \: \dfrac{6}{5}\right)Ora, per determinare la retta del fascio perpendicolare alla bisettrice del primo e del terzo quadrante, dobbiamo anzitutto ricordare l’equazione di tale bisettrice:
y=x
Ora, ricordando quanto sappiamo sulla perpendicolarità tra rette, poiché in questo caso abbiamo {m=1}, una retta perpendicolare alla retta di equazione {y=x} dovrà avere coefficiente angolare {m'=-\dfrac{1}{m}=-\dfrac{1}{1}=-1}.
Poiché il centro del fascio è il punto {C}, si tratterà di scrivere l’equazione di una retta avente coefficiente angolare {m'}, passante per il punto {C} e tale da appartenere al fascio.
Ci viene in aiuto l’equazione di un fascio proprio di rette nella seguente forma esplicita:
y-y_0=m(k)(x-x_0)
Ponendo {m(k)=m'} e sostituendo ad {x_0} e {y_0} le coordinate del punto {C} otteniamo:
y+\dfrac{3}{5}=-1\left( x-\dfrac{6}{5}\right)ovvero:
y+\dfrac{3}{5}=-x+\dfrac{6}{5} \quad \Rightarrow \quad y=-x+\dfrac{3}{5}Così la retta di equazione {y=-x+\dfrac{3}{5}} è la retta del fascio dato tale da essere perpendicolare alla bisettrice del primo e terzo quadrante.
L’ultimo quesito proposto è determinare le equazioni delle rette del fascio tali da distare {\dfrac{1}{5}} dal punto {A=(1,1)}. Per risolvere il problema conviene partire con l’equazione del fascio nella forma:
(2+k)x+(1-2k)y+3k=0
Infatti qui abbiamo i coefficienti {a,b,c} che compaiono nell’equazione di una retta in forma implicita come funzioni del parametro {k}:
\underbrace{(2+k)}_{a(k)}x+\underbrace{(1-2k)}_{b(k)}y+\underbrace{3k}_{c(k)}=0Ora, la distanza punto-retta nel caso di retta con equazione in forma implicita è data da:
d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}Sottolineiamo che è fondamentale ricordare questa formula poiché è molto ricorrente negli esercizi sui fasci di rette.
Ora, le coordinate {x_0} e {y_0} sono note, ed infatti corrispondono alle coordinate del punto {A=(1,1)}. Anche il valore della distanza {d} è noto, ed è pari ad {\dfrac{1}{5}}. Infine, per i coefficienti {a,b,c} abbiamo le rispettive funzioni nel parametro reale {k}, ovvero {a(k), b(k), c(k)}. Così la precedente si riduce ad un’equazione nella sola incognita {k}:
\dfrac{1}{5}=\dfrac{|(2+k)\cdot1+(1-2k)\cdot1+3k|}{\sqrt{(2+k)^2+(1-2k)^2}}In particolare, il nostro obiettivo è determinare i valori del parametro {k} tali che, sostituiti nell’equazione del fascio di rette, consente di determinare le rette del fascio tali da distare {\dfrac{1}{5}} dal punto {A=(1,1)}. E per fare questo, basta risolvere l’equazione appena scritta.
Eseguendo i calcoli al secondo membro dell’equazione abbiamo:
\dfrac{1}{5}=\dfrac{|2+k+1-2k+3k|}{\sqrt{4+4k+k^2+1-4k+4k^2}}ovvero:
\dfrac{1}{5}=\dfrac{|3+2k|}{\sqrt{5k^2+5}} \quad \Rightarrow \quad \dfrac{|3+2k|}{\sqrt{5k^2+5}}-\dfrac{1}{5}=0Mettendo tutti i termini a denominatore comune:
\dfrac{5|3+2k|-\sqrt{5}\sqrt{k^2+1}}{5\sqrt{5}\sqrt{k^2+1}}=0; \qquad \Rightarrow \quad \dfrac{|15+10k|-\sqrt{5}\sqrt{k^2+1}}{5\sqrt{5}\sqrt{k^2+1}}=0A questo punto è importante osservare che il denominatore della frazione algebrica a primo membro è sempre positivo. Infatti, i fattori numerici sono positivi ed inoltre la quantità {k^2+1} è positiva e mai nulla per ogni valore reale del parametro {k}. Di conseguenza è possibile eliminare il denominatore senza alcuna discussione, ritrovandoci con la seguente equazione:
|15+10k|-\sqrt{5}\sqrt{k^2+1}=0Si tratta di un’equazione irrazionale con valori assoluti. Per risolverla possiamo riscriverla nella forma:
\sqrt{5}\sqrt{k^2+1}=|15+10k|Dato che per la presenza del valore assoluto il secondo membro sarà sempre positivo, possiamo elevare entrambi i membri al quadrato senza alcuna ipotesi:
5(k^2+1)=225+100k^2+300k
ovvero:
5k^2+5-225-100k^2-300k=0 \quad \Rightarrow \quad -95k^2-300k-220=0
ossia:
95k^2+300k+220=0
Semplificando:
19k^2+60k+44=0
Vediamo per quali valori di {k} è soddisfatta l’equazione di secondo grado appena scritta:
\begin{align*} &k_{1,2}=\dfrac{-60 \pm \sqrt{60^2-4 \cdot 19 \cdot 44}}{2 \cdot 19 }= \\ \\ & =\dfrac{-60\pm \sqrt{3600-3344}}{38}=\dfrac{-60 \pm \sqrt{256}}{38}=\dfrac{-60\pm\left( 2^8\right)^{\frac{1}{2}}}{38}=\\ \\ & =\dfrac{-60 \pm 16}{38}=\begin{cases} \dfrac{-60+16}{38}=-\dfrac{44}{38}=-\dfrac{22}{19} \\ \\ \dfrac{-60-16}{38}=-\dfrac{76}{38}=-2\end{cases}\end{align*}Così per il parametro {k} abbiamo i valori {k_1=-\dfrac{22}{19}} e {k_2=-2}. Tali valori, se sostituiti all’equazione del fascio, consentono di individuare le particolari rette del fascio che distano {\dfrac{1}{5}} dal punto {A} dato. Riprendiamo quindi l’equazione del fascio, ad esempio nella forma di partenza:
(2+k)x+(1-2k)y+3k=0
Sostituendo {k=-\dfrac{22}{19}} otteniamo:
\begin{align*} &\left( 2-\dfrac{22}{19}\right)x+\left( 1+\dfrac{44}{19}\right)y+3\cdot\left( -\dfrac{22}{19}\right)\end{align*}=0ovvero:
2x-\dfrac{22}{19}x+y+\dfrac{44}{19}y-\dfrac{66}{19}=0ossia:
\left( 2-\dfrac{22}{19}\right)x+\left( 1+\dfrac{44}{19}\right)y-\dfrac{66}{19}=0da cui:
\dfrac{16}{19}x+\dfrac{63}{19}y-\dfrac{66}{19}=0e quindi:
r_1: 16x+63y-66=0
Questa è l’equazione di una retta del fascio tale da distare {\dfrac{1}{5}} dal punto {A}, corrispondente al valore {k_1} del parametro {k}.
Ora, sostituiamo a questo punto sempre nell’equazione del fascio il valore {k_2=-2} del parametro reale {k}:
(2-2)x+(1+4)y+3\cdot(-2)=0
da cui:
y+4y-6=0 \quad \Rightarrow \quad r_2: 5y-6=0
Così l’altra retta del fascio tale da distare {\dfrac{1}{5}} dal punto {A} è la retta {r_2} appena scritta. Abbiamo in questo modo concluso il primo di questa serie di esercizi sui fasci di rette.
Esercizio 2
Proseguiamo gli esercizi sui fasci di rette con il seguente. Stavolta avremo a che fare con un fascio improprio, ovvero un fascio dato da rette tutte parallele tra loro.
Verificare che il fascio di rette {(2-k)x+3(2-k)y+3k=0, \qquad k \in \R \setminus \{2\}} è improprio, e quindi determinare le rette del fascio che distano {\sqrt{10}} dal punto {A=(2,0)}. Stabilire inoltre se la retta {r': x+3y-5=0} appartiene al fascio.
Cominciamo riconducendo l’equazione del fascio alla forma:
a_1x+b_1y+c_1+k\left( a_2x+b_2y+c_2\right)=0
Abbiamo:
\begin{align*} &(2-k)x+3(2-k)y+3k=0; \\ \\ &2x-kx+6y-3ky+3k=0; \\ \\ &2x+6y-kx-3ky+3k=0; \\ \\ &2x+6y+k(-x-3y+3)=0\end{align*}Riconosciamo così le due rette:
r_1: 2x+6y=0; \qquad r_2:-x-3y+3=0
ove {r_2} è la retta esclusa.
Vediamo cosa succede mettendo a sistema le equazioni appena scritte:
\begin{cases} 2x+6y=0 \\ \\ -x-3y+3=0\end{cases}Risolviamo il sistema per riduzione. Cominciamo moltiplicando la seconda equazione per {2}:
\begin{cases} 2x+6y=0 \\ \\ -2x-6y+6=0\end{cases}Sommiamo membro a membro le due equazioni, e sostituiamo la nuova equazione che così otteniamo ad esempio alla seconda equazione a sistema:
\begin{cases} 2x+6y=0 \\ \\ 6=0\end{cases}Dato che l’uguaglianza numerica {6=0} è falsa, il sistema risulta impossibile. A ciò consegue che le due rette {r_1} ed {r_2} non hanno alcun punto di intersezione e sono quindi parallele. Pertanto il fascio dato è improprio.
Ora, per scrivere le equazioni delle rette del fascio che distano {\sqrt{10}} dal punto {A=(2,0)}, dobbiamo anzitutto partire dall’equazione del fascio nella forma data inizialmente:
(2-k)x+3(2-k)y+3k=0
ovvero:
(2-k)x+(6-3k)y+3k=0
Qui abbiamo {a(k)=2-k}, {b(k)=6-3k} e infine {c(k)=3k}. Inoltre il punto dato è {A=(2,0)}, da cui {x_0=2} e {y_0=0}. Disponiamo quindi di tutti i dati per poter imporre la condizione di distanza rispetto al punto {A} sulla generica retta del fascio, in modo da poter ricavare il corrispondente o i corrispondenti valori del parametro reale {k}. In particolare, l’equazione:
d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}nel nostro caso diviene:
\sqrt{10}=\dfrac{|(2-k)\cdot2+(6-3k) \cdot 0+3k|}{\sqrt{\left( 2-k\right)^2+\left( 6-3k\right)^2}}Precisiamo che qui ovviamente i coefficienti {a,b,c} presenti nella formula della distanza punto-retta devono essere visti come funzioni del parametro {k}.
Si tratta a questo punto di risolvere l’equazione appena scritta nell’incognita {k}. Cominciamo eseguendo i calcoli a numeratore e denominatore del secondo membro:
\sqrt{10}=\dfrac{|4-2k+3k|}{\sqrt{4+k^2-4k+36+9k^2-36k}}e quindi:
\sqrt{10}=\dfrac{|4+k|}{\sqrt{10k^2-40k+40}}; \qquad \dfrac{|k+4|}{\sqrt{10} \sqrt{k^2-4k+4}}-\sqrt{10}=0Mettiamo tutti i termini a denominatore comune:
\dfrac{|k+4|-10\sqrt{k^2-4k+4}}{\sqrt{10}\sqrt{k^2-4k+4}}=0Ora è possibile eliminare il denominatore a patto però di porre:
k^2-4k+4> 0
In tal modo imponiamo il denominatore diverso da zero ed inoltre imponiamo la quantità sotto radice non negativa (la radice infatti ha indice pari).
Dalla precedente otteniamo la condizione per i valori di {k}:
k \neq 2
Così sotto tali ipotesi l’equazione precedentemente scritta diviene:
|k+4|-10\sqrt{k^2-4k+4}=0Ovvero:
10\sqrt{k^2-4k+4}=|k+4|Come nell’esercizio precedente, possiamo elevare entrambi i membri al quadrato senza porre alcuna condizione. Infatti, il secondo membro data la presenza del valore assoluto è sempre positivo. Inoltre, abbiamo già posto le opportune condizioni relative al radicando al primo membro. Abbiamo:
100(k^2-4k+4)=k^2+16+8k
Risolvendo l’equazione di secondo grado appena scritta otteniamo (omettiamo i passaggi per brevità):
k_1= \dfrac{16}{11}, \qquad k_2=\dfrac{8}{3}Osserviamo che entrambi i valori ottenuti sono accettabili poiché rispettano la condizione {k \neq 2}.
Questi sono quindi i valori del parametro {k} che corrispondono a due rette del fascio dato entrambe distanti {\sqrt{10}} dal punto {A}. In particolare, sostituendo tali valori nell’equazione del fascio data inizialmente abbiamo, rispettivamente:
\begin{align*} &(2-k)x+3(2-k)y+3k=0 \quad \text{con} \quad k=\dfrac{16}{11} \\ \\ & \Rightarrow \left( 2-\dfrac{16}{11}\right)x+3\left( 2-\dfrac{16}{11}\right)y+\dfrac{48}{11}=0 \\ \\ &\dfrac{6}{11}x+\dfrac{18}{11}y+\dfrac{48}{11}=0 \\ \\ & r_1:x+3y+8=0; \\ \\ &(2-k)x+3(2-k)y+3k=0 \quad \text{con} \quad k=\dfrac{8}{3} \\ \\ & \Rightarrow \left( 2-\dfrac{8}{3}\right)x+\left( 6-3 \cdot \dfrac{8}{3}\right)y+3 \cdot \dfrac{8}{3} =0 \\ \\ & -\dfrac{2}{3}x-2y+8=0 \\ \\ & -x-3y+12=0 \\ \\ & r_2: x+3y-12=0\end{align*}Abbiamo così determinato le equazioni delle due rette {r_1} ed {r_2} del fascio tali da distare {\sqrt{10}} dal punto {A=(2,0)}.
Infine, rimane da stabilire se la retta {r': x+3y-5=0} appartiene al fascio.
Poiché il fascio è improprio, sappiamo che tutte le rette appartenenti al fascio sono parallele tra loro. Così, se la retta {r'} dovesse essere parallela ad esempio ad {r_2}, questa apparterrebbe al fascio dato. Ma come sappiamo, due rette con equazioni date in forma implicita sono tra loro parallele se vale la condizione:
\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}Nel nostro caso abbiamo {a_1=a_2} e {b_1=b_2}. Di conseguenza la condizione è sicuramente soddisfatta.
Così in conclusione la retta {r'}, essendo parallela ad una retta appartenente al fascio dato, appartiene anch’essa a tale fascio.
Esercizio 3
Continuiamo ad affrontare questa serie di esercizi sui fasci di rette con il seguente.
Verificare che il fascio di equazione {(k-3)x-2ky+5-k}=0, \qquad k \in \R è proprio e quindi determinare le equazioni delle rette generatrici e le coordinate del centro del fascio, la retta del fascio passante per l’origine, la retta del fascio parallela alla bisettrice del primo e terzo quadrante ed infine la retta del fascio perpendicolare alla retta {r': x-4y=0}.
L’esercizio appena proposto, come nel caso dei precedenti esercizi sul fascio di rette, richiede anzitutto di ricondurre l’equazione del fascio alla forma:
a_1x+b_1y+c_1+k\left( a_2x+b_2y+c_2\right)=0, \qquad k \in \R
In tal modo sarà possibile determinare le equazioni delle rette generatrici del fascio. Abbiamo:
\begin{align*} & (k-3)x-2ky+5-k=0; \\ \\ & kx-3x-2ky+5-k=0; \\ \\ &-3x+5+kx-2ky-k=0; \\ \\ & -3x+5+k(x-2y-1)=0\end{align*}Di conseguenza le equazioni delle rette generatrici del fascio sono:
r_1: -3x+5, \qquad r_2: x-2y-1=0
ove {r_2} è la retta esclusa.
Per determinare le coordinate del centro del fascio come al solito dobbiamo calcolare, se esistono, le coordinate del punto di intersezione tra le rette generatrici del fascio:
\begin{cases} -3x+5=0 \quad \rightarrow \quad x=\dfrac{5}{3} \\ \\ x-2y-1=0 \quad \rightarrow \quad y=\dfrac{1}{3} \end{cases}Così il fascio è proprio ed ha come centro il punto {C} di coordinate:
C=\left( \dfrac{5}{3}, \dfrac{1}{3}\right)Ora, determiniamo l’equazione della retta del fascio passante per l’origine. L’obiettivo è scrivere l’equazione di una retta appartenente al fascio dato ed allo stesso tempo tale da passare per l’origine, ovvero per il punto {O=(0,0)}.
Quindi, data l’equazione del fascio ad esempio nella forma iniziale:
(k-3)x-2ky+5-k=0
si tratterà di sostituire alle variabili {x} ed {y} rispettivamente le coordinate dell’origine, e quindi ricavare il corrispondente valore del parametro {k}. In tal modo avremo determinato il valore del parametro reale {k} corrispondente alla retta del fascio passante per l’origine. Si ha:
(k-3) \cdot 0 -2 k \cdot 0 +5-k=0 \quad \Rightarrow \quad 5-k=0 \quad \Rightarrow \quad k=5
Infine sostituendo il valore di {k} appena determinato nell’equazione del fascio (ad esempio nella forma iniziale) otteniamo l’equazione della retta {r'} cercata:
\small (k-3)x-2ky+5-k=0 \quad \text{con} \quad k= 5 \quad \Rightarrow \: 2x-10y=0 \quad \Rightarrow \: r':x-5y=0In alternativa, avremmo anche potuto utilizzare l’equazione della retta del piano passante per due punti:
\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}Infatti, ciò che ricerchiamo è una retta passante per il centro del fascio e per l’origine. Di conseguenza, sostituendo nella formula le coordinate rispettivamente del centro {C} e dell’origine {O} possiamo ricavare l’equazione della retta del fascio passante per l’origine. Tuttavia, attenzione. Come già sottolineato nella lezione teorica sui fasci di rette, procedendo in questo modo occorre poi verificare che l’equazione ottenuta non corrisponda a quella della retta esclusa.
Con questo metodo alternativo, nel nostro caso abbiamo, sostituendo ad esempio ad {x_1} ed {y_1} le coordinate del centro del fascio e ad {x_2} ed {y_2} le coordinate dell’origine:
\dfrac{y-\frac{1}{3}}{\frac{1}{3}}=\dfrac{x-\frac{5}{3}}{\frac{5}{3}}da cui:
3y-1=\dfrac{3}{5}x-1 \quad \Rightarrow \quad 3x-15y=0 \quad \Rightarrow \quad r':x-5y=0Ora, l’equazione della retta esclusa dal fascio è come sappiamo {r_2: x-2y-1=0}. Tale equazione è chiaramente differente da quella della retta {r'}, così in conclusione possiamo affermare che la retta {r'} appartiene al fascio, ed è proprio la retta cercata. Il risultato coincide, effettivamente, con quello ottenuto con il metodo precedente.
A questo punto proseguiamo l’esercizio sul fascio di rette in esame determinando l’equazione della retta del fascio tale da essere parallela alla bisettrice del primo e terzo quadrante. Ricordiamo anzitutto che l’equazione della bisettrice del primo e del terzo quadrante è:
y=x
Tale equazione è della forma {y=mx+q}, con {m=1} e {q=0}. Una qualunque retta parallela a tale bisettrice dovrà quindi avere necessariamente coefficiente angolare {m=1}. Di conseguenza il nostro obiettivo è determinare l’equazione di una retta del fascio tale ad avere coefficiente angolare pari a {1}.
Riprendiamo ancora l’equazione del fascio nella sua forma iniziale:
(k-3)x-2ky+5-k=0, \qquad k \in \R
Tale equazione è della forma {ax+by+c=0}, ma con coefficienti {a,b,c} dipendenti dal parametro {k}. Ricordiamo in generale che per equazioni di questa forma è possibile esprimere il coefficiente angolare della retta corrispondente come:
m=-\dfrac{a}{b}così evidentemente nel caso dei fasci di rette la precedente si può riesprimere come:
m=-\dfrac{a(k)}{b(k)}Quindi nel nostro caso, essendo {a(k)=k-3} e {b(k)=-2k}:
m=-\dfrac{k-3}{-2k}; \quad \Rightarrow \quad m=\dfrac{k-3}{2k}Ma dato che il valore del coefficiente angolare deve essere {1}, l’ultima equazione scritta diviene:
\dfrac{k-3}{2k}=1Ci ritroviamo così con un’equazione di primo grado fratta nella sola incognita {k}. Per risolverla, prima di tutto mettiamo tutti i termini a denominatore comune:
\begin{align*} &\dfrac{k-3}{2k}-1=0; \qquad \dfrac{k-3-2k}{2k}=0\end{align*}Ora per {k \neq 0} possiamo eliminare il denominatore:
k-3-2k=0, \qquad \text{con} \quad k \neq 0Otteniamo quindi:
-k-3=0 \quad \Rightarrow \quad k=-3
Questo è il valore del parametro reale {k} che corrisponde alla retta del fascio tale da essere parallela alla bisettrice del primo e terzo quadrante. Così, sostituendo tale valore di {k} nell’equazione del fascio otteniamo:
\begin{align*} & (k-3)x-2ky+5-k=0 \quad \text{con} \quad k=-3 \\ \\ & \Rightarrow \quad -6x+6y+8=0 \\ \\ & \Rightarrow 3x-3y-4=0\end{align*}E questa è l’equazione della retta cercata.
Per rispondere a tutti i quesiti dell’esercizio, rimane infine da determinare l’equazione della retta del fascio tale da essere perpendicolare alla retta {r': x-4y=0}.
In forma esplicita, l’equazione della retta {r'} diviene:
r':y=\dfrac{1}{4}xOra l’equazione è della forma {y=mx+q} e di conseguenza il coefficiente angolare della retta {r'} è {m'=\dfrac{1}{4}}. Ricordando la condizione di perpendicolarità tra rette, una qualunque retta perpendicolare ad {r'} avrà coefficiente angolare {-\dfrac{1}{m'}}, e quindi in questo caso {-4}.
Il problema si riconduce quindi alla determinazione dell’equazione della retta del fascio tale da avere coefficiente angolare {-4}. Allo scopo possiamo riutilizzare la seguente equazione precedentemente scritta, la quale esprime il coefficiente angolare delle rette del fascio in funzione del parametro reale {k} :
m=\dfrac{k-3}{2k}Sostituendo ad {m} il valore {-4} otteniamo l’equazione:
\dfrac{k-3}{2k}=-4Da cui:
\dfrac{k-3+8k}{2k}=0 \quad \Rightarrow \quad k=\dfrac{1}{3}, \qquad (k \neq 0)Così sostituendo nell’equazione del fascio (ad esempio nella forma iniziale) otteniamo in conclusione l’equazione della retta del fascio tale da essere perpendicolare alla retta {r'}:
\begin{align*} & (k-3)x-2ky+5-k=0 \quad \text{con} \quad k= \dfrac{1}{3} \\ \\ & \Rightarrow \quad -\dfrac{8}{3}x-\dfrac{2}{3}y+\dfrac{14}{3}=0 \\ \\ & \Rightarrow 4x+y-7=0\end{align*}Esercizio 4
Proseguiamo ancora gli esercizi sui fasci di rette con il seguente, il quale propone anche il problema della determinazione delle equazioni delle rette di un dato fascio tali da individuare su un asse cartesiano un segmento di una certa lunghezza.
Verificare che il fascio di rette di equazione {kx+3(2-k)y+1-k = 0, \qquad k \in \R} è proprio, e quindi determinare le generatrici e il centro del fascio, l’equazione della retta del fascio passante per il punto {A=(-2, 1)}, l’equazione della retta del fascio parallela alla retta {2x+y+4=0}, l’equazione della retta del fascio perpendicolare alla retta {y=-\dfrac{1}{3}x} ed infine le equazioni delle rette del fascio che staccano sull’asse {y} un segmento di lunghezza {\dfrac{4}{3}}.
Come al solito, cominciamo con il riesprimere l’equazione del fascio dato nella forma {a_1x+b_1y+c_1+k(a_2x+b_2y+c_2)=0}:
\begin{align*} &kx+3(2-k)y+1-k = 0; \\ \\ & kx+6y-3ky+1-k=0; \\ \\ & 6y+1+kx-3ky-k=0; \\ \\ & 6y+1+k(x-3y-1)=0\end{align*}Le equazioni delle rette generatrici del fascio sono di conseguenza:
r_1: 6y+1=0, \qquad r_2:x-3y-1=0
ove come al solito {r_2} è la retta esclusa.
Per verificare che il fascio dato è proprio, procediamo ancora una volta ricercando il punto di intersezione tra le due rette {r_1} ed {r_2}:
\begin{cases} 6y+1=0 \quad \rightarrow \quad y=-\dfrac{1}{6}\\ \\ x-3y-1=0 \quad \rightarrow \quad x=3y+1 \quad \rightarrow \quad x=\dfrac{1}{2}\end{cases}Quindi il fascio è proprio ed ha come centro il punto {C=\left( \dfrac{1}{2}, -\dfrac{1}{6}\right)}.
Si tratta ora di determinare l’equazione della retta del fascio tale da passare per il punto {A=(-2,1)}. Allo scopo basta sostituire le coordinate del punto {A} nell’equazione del fascio, ad esempio nella forma {6y+1+k(x-3y-1)=0}, e quindi ricavare il corrispondente valore del parametro reale {k}:
\begin{align*} &6y+1+k(x-3y-1)=0\quad \text{con} \quad x=-2, \: y=1 \\ \\ & \Rightarrow6+1+k(-2-3-1)=0; \\ \\ & 6+1-2k-3k-k=0 \quad \Rightarrow \quad k=\dfrac{7}{6}\end{align*}Ora sostituendo il valore appena trovato per il parametro {k} nell’equazione del fascio abbiamo:
\begin{align*} & 6y+1+\dfrac{7}{6}(x-3y-1)=0 \quad \Rightarrow \quad 6y+1+\dfrac{7}{6}x-\dfrac{21}{6}y-\dfrac{7}{6}=0 \quad \Rightarrow \\ \\ & \Rightarrow \quad 36y+6+7x-21y-7=0 \quad \Rightarrow \quad 7x+15y-1=0 \end{align*}L’equazione appena scritta è quella cercata, ovvero è l’equazione della retta del fascio passante per il punto {A}.
Determiniamo ora l’equazione della retta del fascio tale da essere parallela alla retta di equazione {2x+y+4=0}. Cominciamo riconducendo quest’ultima equazione alla forma esplicita:
y=-2x+4
da cui segue per tale retta il valore del coefficiente angolare {m=-2}. Di conseguenza vista la condizione di parallelismo tra rette, dovremo ricercare la particolare retta del fascio tale da avere coefficiente angolare uguale a {-2}.
Come fatto negli esercizi precedenti, ricaviamo anzitutto l’espressione del coefficiente angolare {m} della generica retta del fascio dato in funzione del parametro reale {k}. Partendo dall’equazione del fascio nella forma iniziale, abbiamo:
m=-\dfrac{k}{3(2-k)} \quad \Rightarrow \quad m=\dfrac{k}{3(k-2)}Nel nostro caso dovendo imporre {m=-2}:
-2=\dfrac{k}{3(k-2)} \quad \Rightarrow \quad \dfrac{k+6(k-2)}{3(k-2)}=0 \quad \Rightarrow \quad k=\dfrac{12}{7}Sostituendo il valore appena trovato per il parametro {k} nell’equazione del fascio abbiamo:
\begin{align*} & 6y+1+\dfrac{12}{7}(x-3y-1)=0 \quad \Rightarrow \quad 6y+1+\dfrac{12}{7}x-\dfrac{36}{7}y-\dfrac{12}{7}=0 \quad \Rightarrow \quad \\ \\ & \Rightarrow \quad 42y+7+12x-36y-12=0 \quad \Rightarrow \quad 12x+6y-5=0 \end{align*}E questa è l’equazione della retta del fascio tale da essere parallela alla retta {y=-2x+4}.
Proseguiamo determinando la retta del fascio perpendicolare alla retta di equazione {y=-\dfrac{1}{3}x}. Come nell’esercizio precedente, qui basta ricordare la condizione di perpendicolarità tra rette, per la quale concludiamo immediatamente che una qualunque retta perpendicolare alla retta data dovrà avere coefficiente angolare {m=3} (l’inverso del reciproco del coefficiente angolare della retta data).
Sfruttando l’espressione precedentemente scritta del coefficiente angolare di una generica retta del fascio in funzione del parametro {k} abbiamo:
\begin{align*} &m=\dfrac{k}{3(k-2)} \quad \text{con} \quad m=3 \\ \\ & \Rightarrow \quad \dfrac{k}{3(k-2)}=3 \quad \Rightarrow \quad k-9(k-2)=0 \quad \text{con} \quad k \neq 2 \\ \\ & \Rightarrow 8k=18 \quad \Rightarrow \quad k=\dfrac{9}{4}\end{align*}Da cui sostituendo il valore appena trovato per il parametro nell’equazione del fascio otteniamo l’espressione dell’equazione della retta cercata:
\begin{align*} &\begin{align*} & 6y+1+\dfrac{9}{4}(x-3y-1)=0 \quad \Rightarrow \quad 6y+1+\dfrac{9}{4}x-\dfrac{27}{4}y-\dfrac{9}{4}=0 \\ \\ & \Rightarrow \quad 24y+4+9x-27y-9=0 \quad \Rightarrow \quad 9x-3y-5=0 \end{align*}\end{align*}Ci avviamo ora alla conclusione di questo esercizio sui fasci di rette, rispondendo all’ultimo quesito sulla determinazione delle equazioni delle rette del fascio che staccano sull’asse {y} un segmento di lunghezza {\dfrac{4}{3}}.
Osserviamo anzitutto che in generale una retta “stacca” sull’asse {y} un segmento di lunghezza data se la distanza compresa tra il punto di intersezione retta-asse {y} e l’origine degli assi è uguale proprio alla lunghezza del segmento stesso.
Così fra le rette di un fascio proprio esisteranno sempre due rette che staccano sull’asse {y} un segmento avente una certa lunghezza.
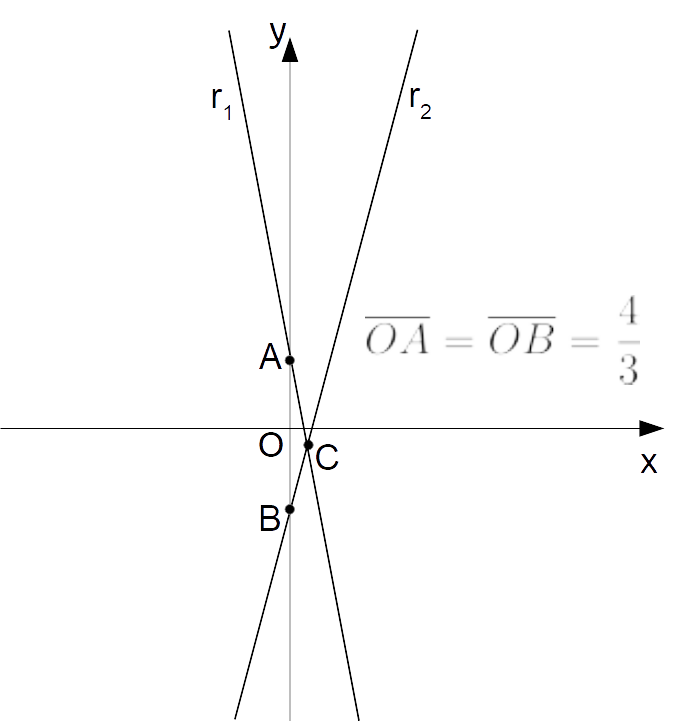
Come si può vedere analizzando la figura, il nostro obiettivo è determinare le equazioni di due rette del fascio alle quali appartengano rispettivamente il punto {A=\left( 0, \dfrac{4}{3}\right)} e il punto {B=\left( 0, -\dfrac{4}{3}\right)}. Per cui pur potendo individuare nella figura dei triangoli rettangoli non c’è alcun bisogno di scomodare la trigonometria. 😉
Cominciamo sostituendo le coordinate del punto {A} nell’equazione del fascio:
\begin{align*} &6y+1+k(x-3y-1)=0\quad \text{con} \quad x=0, \: y=\dfrac{4}{3} \\ \\ & 6 \cdot \dfrac{4}{3} + 1 + k\left( 0-3 \cdot \dfrac{4}{3} - 1\right)=0; \\ \\ & 9+k\cdot(-5)=0 \quad \Rightarrow \quad k=\dfrac{9}{5}\end{align*}Sostituendo il valore appena trovato sempre nell’equazione del fascio (nella forma più conveniente) otteniamo:
\begin{align*}& 6y+1+k(x-3y-1)=0 \quad \text{con}\quad k=\dfrac{9}{5} \\ \\ & \Rightarrow 6y+1+\dfrac{9}{5}x-\dfrac{27}{5}y-\dfrac{9}{5} =0; \\ \\ & 30y+5+9x-27y-9=0; \\ \\ & r_1: 9x+3y-4=0\end{align*}Abbiamo così determinato l’equazione della retta {r_1}. Concludiamo con l’equazione della retta {r_2}, procedendo in modo del tutto simile. Sostituiamo anzitutto le coordinate del punto {B} nell’equazione del fascio, in modo da ricavare il valore corrispondente del parametro {k}:
\begin{align*} &6y+1+k(x-3y-1)=0\quad \text{con} \quad x=0, \: y=-\dfrac{4}{3} \\ \\ & 6 \cdot \left(-\dfrac{4}{3} \right) + 1 + k\left( 0+3 \cdot \dfrac{4}{3} - 1\right)=0; \\ \\ & -7+k\cdot3 =0 \quad \Rightarrow \quad k=\dfrac{7}{3}\end{align*}Infine sostituendo il valore del parametro {k} nell’equazione del fascio nella forma più conveniente:
\begin{align*}& 6y+1+k(x-3y-1)=0 \quad \text{con}\quad k=\dfrac{7}{3} \\ \\ & \Rightarrow 6y+1+\dfrac{7}{3}x-\dfrac{21}{3}y-\dfrac{7}{3} =0; \\ \\ & 18y+3+7x-21y-7=0; \\ \\ & r_2: 7x-3y-4=0\end{align*}Con ciò abbiamo concluso anche questo esercizio sui fasci di rette. Osserviamo soltanto che, come per l’esercizio 3, avremmo anche potuto utilizzare per gli ultimi due quesiti la formula della retta passante per due punti. Tuttavia, lo ricordiamo ancora, tale metodo richiede obbligatoriamente di verificare che le equazioni ottenute non corrispondano all’equazione della retta esclusa.
Esercizio 5
Prima di concludere questa serie di esercizi sui fasci di rette, vogliamo ancora presentare un paio di esercizi. Nel seguente mostreremo in particolare come determinare l’equazione della bisettrice di un angolo avente per lati due rette di un fascio e inoltre come calcolare le coordinate del simmetrico di un punto rispetto ad una retta di un fascio.
Dato il fascio di rette di equazione {(k-1)x-(k-2)y+k=0, \qquad k \in \R}determinare il centro del fascio, l’equazione della retta {r} del fascio passante per l’origine, l’equazione della retta {s} del fascio passante per il punto {A(0,3)}, le equazioni delle bisettrici degli angoli formati dalle rette {r} ed {s} stesse, le rette del fascio che hanno distanza {1} dall’origine ed infine le coordinate del simmetrico di {A} rispetto ad {r}.
Cominciamo determinando le coordinate del centro del fascio. Allo scopo è necessario come ormai ben sappiamo determinare le equazioni delle rette generatrici:
\begin{align*} &(k-1)x-(k-2)y+k=0; \\ \\ & kx-x-ky+2y+k=0; \\ \\ & -x+2y+k(x-y+1)=0;
\end{align*}Le rette generatrici del fascio sono dunque {r_1: -x+2y=0} e {r_2:x-y+1=0}, ove quest’ultima è la retta esclusa.
Ricerchiamo ora il centro del fascio:
\begin{cases} -x+2y=0 \\ \\ x-y+1=0\end{cases} \quad \Rightarrow \quad \begin{cases} y=-1 \\ \\ x=-2\end{cases}Di conseguenza il centro del fascio è dato dal punto {C=(-2, -1)}.
Ora ricerchiamo le equazioni delle rette {r} ed {s} passanti rispettivamente per l’origine {O=(0,0)} e per il punto {A)(0,3)}. Scegliamo in questo caso di utilizzare la formula della retta passante per due punti, procedendo poi alla verifica relativa alla retta esclusa.
La retta {r} dovrà passare necessariamente per il centro del fascio {C} e per l’origine:
\begin{align*} & \dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}; \qquad \dfrac{y-(-1)}{0-(-1)}=\dfrac{x-(-2)}{0-(-2)} \\ \\ & \dfrac{y+1}{1}=\dfrac{x+2}{2}; \qquad 2y+2-x-2=0; \qquad r: x-2y=0\end{align*}Osserviamo che l’equazione appena ottenuta non corrisponde all’equazione della retta esclusa {r_2}. Di ciò siamo certi poiché entrambe le equazioni condividono lo stesso coefficiente per la {x} ma hanno differente coefficiente per la {y} e differente termine noto. Di conseguenza, possiamo affermare che l’equazione appena scritta per {r} è effettivamente l’equazione della retta del fascio tale da passare per l’origine.
In modo del tutto simile determiniamo l’equazione della retta {s} passante per il punto {A=(0,3)}:
\begin{align*} & \dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}; \qquad \dfrac{y-(-1)}{3-(-1)}=\dfrac{x-(-2)}{0-(-2)}; \\ \\ & \dfrac{y+1}{4}=\dfrac{x+2}{2}; \qquad y+1-2x-4=0; \qquad s:2x-y+3=0 \end{align*}Per verificare che l’equazione della retta {s} sia differente dall’equazione della retta esclusa {r_2}, dividiamo tutti i termini al primo membro dell’equazione della retta {s} per {2}. In questo modo il coefficiente della {x} diverrà {1} come nell’equazione della retta {r_2}:
s:x-\dfrac{1}{2}y+\dfrac{3}{2}=0Come possiamo vedere il termine in {y} e il termine noto differiscono da quelli dell’equazione della retta esclusa. Di conseguenza, possiamo affermare che {s} è effettivamente la retta del fascio tale da passare per il punto {A}.
Ora, per scrivere le equazioni delle bisettrici degli angoli formati dalle due rette, dobbiamo anzitutto avere presente la definizione di bisettrice di un angolo formato da due rette.
Prima di tutto, ricordiamo che due rette formano nel piano quattro angoli, a due a due uguali. Così, nel nostro caso dovremo considerare due angoli (vedi figura).

Ora, il nostro obiettivo è determinare le equazioni delle bisettrici {b_1} e {b_2}:
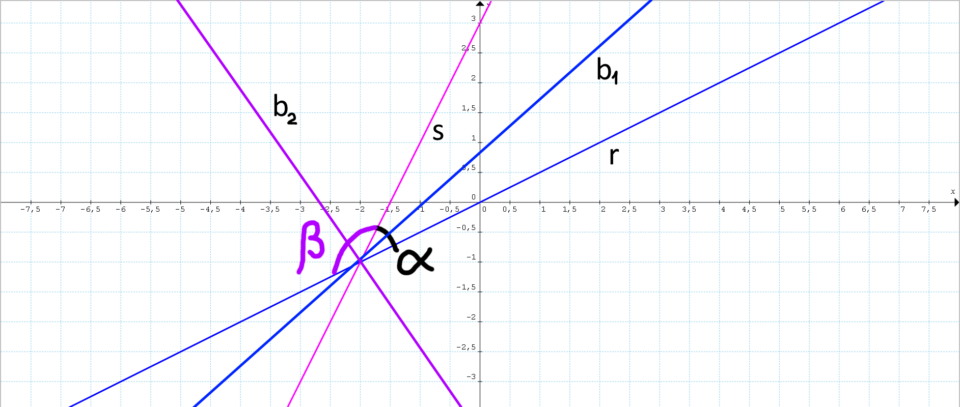
Si tratta in particolare delle rette bisettrici degli angoli aventi per lati le rette {r} ed {s}, considerando una sola coppia di angoli aventi differente ampiezza.
Per determinare le equazioni delle bisettrici di tali angoli, occorre ricordare la seguente definizione di bisettrice di un angolo.
La bisettrice di un angolo è una particolare retta data dal luogo dei punti aventi la stessa distanza dai lati dell’angolo.
Ora, nel nostro caso gli angoli hanno per lati rispettivamente la retta {r} ed {s}. Così, il nostro obiettivo è scrivere le equazioni di due rette, ciascuna avente tutti i punti equidistanti da {r} e da {s}.
Le equazioni cercate si ricavano a partire da un’uguaglianza del tipo:
d(r, P)=d(s,P)
ove {P} è un generico punto appartenente alla bisettrice dell’angolo considerato. In particolare, ricordando la formula della distanza punto-retta ed indicando con {x} e {y} le coordinate del generico punto {P} della retta bisettrice:
\dfrac{|a_rx+b_ry+c_r|}{\sqrt{a_r^2+b_r^2}}=\dfrac{|a_sx+b_sy+c_s|}{\sqrt{a_s^2+b_s^2}}Osserviamo che nell’uguaglianza appena scritta le variabili {x} e {y} sono indeterminate, poiché l’uguaglianza è valida per un qualunque punto della retta bisettrice considerata. Invece, i coefficienti {a,b,c} sono i coefficienti delle equazioni delle rette {r} ed {s}, in base al pedice corrispondente. Di conseguenza, effettuando le opportune sostituzioni e manipolazioni algebriche sull’equazione appena scritta sarà possibile ricavare le due equazioni delle bisettrici degli angoli nelle figure. Abbiamo:
\begin{align*} &\dfrac{|x-2y|}{\sqrt{1^2+(-2)^2}}=\dfrac{|2x-y+3|}{\sqrt{2^2+(-1)^2}}; \\ \\ & \dfrac{|x-2y|}{\sqrt{5}}=\dfrac{|2x-y+3|}{\sqrt5}; \\ \\ & \begin{cases} b_1: x-2y=2x-y+3 \\ \\ b_2: \underbrace{ -x+2y}_{\text{opposto di }x-2y}=2x-y+3 & \end{cases} \\ \\ & \begin{cases} b_1:x+y+3=0 \\ \\ b_2:3x-3y+3=0 \quad \rightarrow \quad b_2:x-y+1=0\end{cases}\end{align*}Per chiarire gli ultimi passaggi, osserviamo che abbiamo eliminato i simboli di modulo considerando i due soli distinti casi ove i segni delle quantità in modulo sono tra loro concordi (retta bisettrice {b_1}) e discordi (retta bisettrice {b_2)}. In altre parole, l’uguaglianza:
\dfrac{|x-2y|}{\sqrt{5}}=\dfrac{|2x-y+3|}{\sqrt5}equivale a scrivere:
\pm\left( x-2y\right)=2x-y+3
da cui segue, come nei precedenti passaggi:
\begin{cases} b_1: x-2y=2x-y+3 \\ \\ b_2: -x+2y=2x-y+3 & \end{cases}Ricordiamo ancora che nel nostro particolare caso le incognite {x} e {y} sono delle indeterminate. Infatti, queste rappresentano le coordinate di un qualunque punto appartenente alle bisettrici. Per cui di esse non va ricercato il valore.
Ora non resta che tracciare nel grafico le equazioni delle due rette bisettrici ottenute ed eventualmente cambiarne il nome rispetto alle precedenti figure, in modo da essere coerenti con le equazioni ottenute:
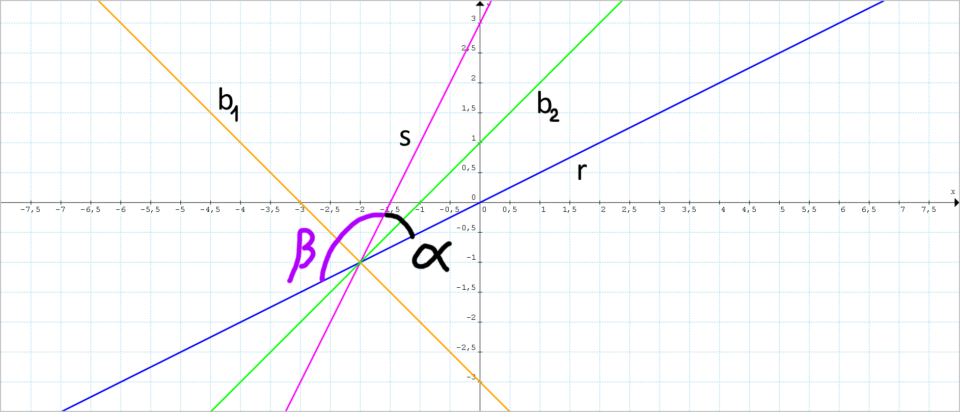
Così in conclusione abbiamo le due seguenti equazioni delle bisettrici degli angoli {\alpha} e {\beta}:
b_1:x+y+3=0; \qquad b_2: x-y+1=0
Infine, precisiamo ancora che gli angoli formati dalle rette {r} ed {s} da considerare a lato pratico sono soltanto due. Infatti, i rimanenti due angoli formati dalle rette {r} ed {s} sono rispettivamente opposti ad {\alpha} e {\beta}. Trattandosi quindi di angoli aventi le stesse ampiezze di {\alpha} e {\beta}, questi hanno come bisettrici di nuovo le rette {b_1} e {b_2} già individuate.
Proseguiamo questo esercizio sui fasci di rette rispondendo al penultimo quesito. Vediamo quindi di scrivere le equazioni delle rette del fascio tali da distare {1} dall’origine degli assi cartesiani.
Come visto nel primo esercizio di questa serie di esercizi sui fasci di rette, la formula da utilizzare è quella relativa alla distanza punto-retta, ovvero:
d=\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} \qquad (*)Nel nostro caso dobbiamo porre {d=1}, quindi sostituire a {x_0} ed {y_0} le coordinate dell’origine, ed infine sostituire ai coefficienti {a,b,c} i coefficienti funzioni del parametro {k} reale {a(k), b(k), c(k)} relativi al fascio considerato.
Per ottenere i valori delle funzioni {a(k), b(k), c(k)} riprendiamo l’equazione del fascio nella sua forma iniziale:
(k-1)x-(k-2)y+k=0
Qui, attenzione. Poiché la forma generale di tale equazione è del tipo:
a(k)x+b(k)y+c(k)
dobbiamo stare attenti ai segni nel caso del coefficiente {b(k)}. In particolare avremo:
a(k)=k-1; \qquad b(k)=2-k; \qquad c(k)=k
Così tenendo conto di tutto quanto sin qui detto l’uguaglianza * diviene:
1=\dfrac{|(k-1) \cdot 0+(2-k) \cdot 0+k|}{\sqrt{(k-1)^2+(2-k)^2}}ovvero:
1=\dfrac{|k|}{\sqrt{(k-1)^2+(2-k)^2}}Svolgendo i passaggi secondo la stessa procedura del primo esercizio di questa scheda abbiamo:
\begin{align*} &1= \dfrac{|k|}{\sqrt{k^2+1-2k+4+k^2-4k}}; \\ \\ & 1=\dfrac{|k|}{\sqrt{2k^2-6k+5}}; \\ \\ &\sqrt{2k^2-6k+5} =|k|, \qquad (\forall k); \\ \\ & 2k^2-6k+5=k^2; \\ \\ & k^2-6k+5=0 \quad \Rightarrow \quad k_1=1, \quad k_2 = 5\end{align*}Precisiamo che nei passaggi è stato possibile eliminare il denominatore senza imporre alcuna condizione sul parametro {k} in quanto il radicando {2k^2-6k+5} non si annulla per nessun valore reale di {k}.
Ora, quelli ottenuti sono i due valori del parametro reale {k} ai quali corrispondono le equazioni delle rette del fascio distanti {1} dall’origine. Sostituendo così i valori di {k} ottenuti nell’equazione del fascio (ad esempio data nella forma iniziale) abbiamo:
\begin{align*} & (k-1)x-(k-2)y+k=0 \quad \text{con} \quad k=1 \\ \\ & \Rightarrow y+1=0 \quad \Rightarrow \quad y=-1;\\ \\ & (k-1)x-(k-2)y+k=0 \quad \text{con} \quad k=5 \\ \\ & \Rightarrow 4x-3y+5=0\end{align*}Quindi rispondendo al quesito in esame le rette del fascio tali da distare {1} dall’origine hanno equazioni rispettivamente {y=-1} e {4x-3y+5=0}.
Veniamo ora all’ultimo quesito, ovvero la determinazione delle coordinate del punto {A'} simmetrico ad {A} rispetto alla retta {r}.
Osserviamo prima di tutto che il simmetrico di un punto rispetto ad una retta giacerà necessariamente sulla perpendicolare alla retta data (vedi figura a seguire).
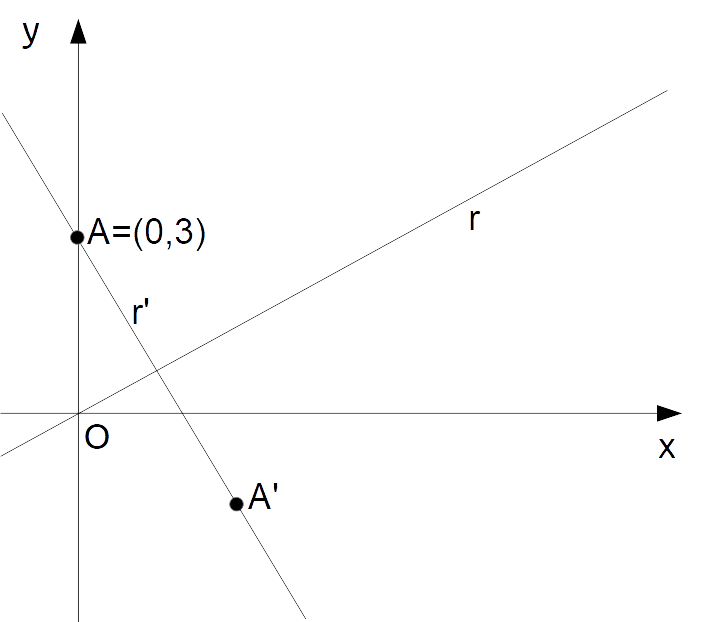
Così il primo passo è ricavare, a partire dall’equazione della retta {r}, quella della retta {r'} ad essa perpendicolare. Ricordando la relazione di perpendicolarità fra rette, e data l’equazione della retta {r} già scritta in precedenza si ha:
r: x-2y=0 \quad \Rightarrow \quad r': 2x+y+c=0
Ricordiamo che data l’equazione implicita di una retta, l’equazione della sua perpendicolare si ottiene scambiando fra loro i coefficienti dei termini in {x} ed {y} e cambiando il segno di uno ed uno solo di essi.
Ora, quella che abbiamo scritto è l’equazione di una generica retta perpendicolare ad {r}. Il nostro obiettivo è adesso determinare il valore di {c} per il quale la retta {r'} effettivamente passi per il punto {A}. Allo scopo basta imporre la condizione di appartenenza del punto {A} alla retta {r'}, e quindi ricavare il valore corrispondente di {c}. Abbiamo:
2 \cdot 0+1 \cdot 3 + c = 0 \quad \Rightarrow \quad c=-3
Di conseguenza l’equazione della retta {r'} diviene:
r':2x+y-3=0
Ora, il punto {A'} dovrà avere rispetto alla retta {r} la stessa distanza che ha da essa il punto {A}. Quindi dovrà valere l’uguaglianza:
d(A,r)=d(A',r)
E’ immediato calcolare {d(A,r)}, ovvero la distanza del punto {A} dalla retta {r}, in quanto disponiamo di tutti i dati:
d(A,r)=\dfrac{|x-2y|}{\sqrt{a_r^2+b_r^2}}=\dfrac{|0-2 \cdot 3|}{\sqrt{1^2+(-2)^2}}=\dfrac{6}{\sqrt{5}}Così sostituendo il valore di {d(A,r)} appena ricavato nell’uguaglianza fra distanze scritta in precedenza abbiamo:
d(A',r)=\dfrac{6}{\sqrt{5}}Le coordinate del punto {A'} sono incognite ma l’equazione della retta {r} è nota. Così intanto possiamo scrivere, riscrivendo il primo membro utilizzando la formula distanza-retta:
\dfrac{|x'-2y'|}{\sqrt{5}}=\dfrac{6}{\sqrt{5}}ove {x'} ed {y'} sono le coordinate del punto {A'}.
Ora, ci ritroviamo sfortunatamente con due incognite, ma niente panico. Per la condizione di appartenenza del punto {A'} alla retta {r'} si ha:
2x'+y'-3=0
da cui ad esempio:
y'=3-2x'
Di conseguenza sostituendo ad {y'} l’espressione appena ottenuta in funzione di {x'}, la precedente equazione in due incognite si riduce alla seguente equazione in una sola incognita:
\dfrac{|x'-2(3-2x')|}{\sqrt{5}}=\dfrac{6}{\sqrt{5}}da cui, sviluppando i calcoli:
|x'-6+4x'|=6 \quad \Rightarrow \quad |5x'-6|=6
Risolvendo l’equazione con valore assoluto appena scritta otteniamo due valori per {x'}, entrambi accettabili:
\begin{align*} &5x'-6 > 0 \quad \Rightarrow \quad 5x'-6=6 \quad \Rightarrow \quad x_1'=\dfrac{12}{5}; \\ \\ & 5x'-6 < 0 \quad \Rightarrow \quad 6-5x'=6 \quad \Rightarrow \quad x_2'=0;\end{align*}Tenendo conto che, come scritto in precedenza, {y'=3-2x'}, abbiamo:
y_1'=3-2 \cdot \dfrac{12}{5}=-\dfrac{9}{5}; \qquad y_1''=3-2 \cdot 0 =3Ora, le coordinate {x_1''} e {y_1''} sono quelle del punto {A}. Di nostro interesse sono invece le coordinate {x_1'} ed {y_1'}, che corrispondono alle coordinate cercate del punto {A'}. Per cui abbiamo in conclusione:
A'=\left( \dfrac{12}{5}, -\dfrac{9}{5}\right)Esercizio 6
Siamo ora all’ultimo degli esercizi sui fasci di rette della scheda. In questo caso avremo a che fare con un fascio di rette degenere.
Classificare il fascio di equazione {(2k+1)x+(4k+2)y+8k+4=0, \qquad k \in \R}
Ricerchiamo le rette generatrici del fascio, esattamente come fatto negli esercizi precedenti:
\begin{align*} &(2k+1)x+(4k+2)y+8k+4=0; \\ \\ & 2kx+x+4ky+2y+8k+4=0;\\ \\ & x+2y+4+k(2x+4y+8)=0\end{align*}Di conseguenza le rette generatrici del fascio sono:
r_1: x+2y+4=0, \qquad r_2: 2x+4y+8=0
Proviamo a ricercare l’eventuale punto di intersezione tra le due rette:
\small \begin{cases} x+2y+4=0 \\ \\ 2x+4y+8=0\end{cases} \quad \Rightarrow \quad \begin{cases} 2x+4y+8=0 \\ \\ 2x+4y+8=0 \end{cases} \quad \Rightarrow \quad \begin{cases} 0=0 \\ \\ 2x+4y+8=0\end{cases}Poiché ritroviamo nel sistema l’identità {0=0}, il sistema stesso è indeterminato. Ciò significa che esistono infiniti punti di intersezione tra le due rette generatrici del fascio, e di conseguenza il fascio è degenere. In altre parole, poiché le rette del fascio hanno tutti i loro punti in comune, a lato pratico il fascio stesso è in realtà da considerarsi come una retta.
Conclusioni
Gli esercizi sui fasci di rette del tipo generale, come quelli svolti in questa scheda, richiedono una buona conoscenza di tutti gli argomenti sin qui trattati sulla retta nel piano cartesiano. In caso di dubbi il consiglio è dunque quello di rivedere i vari argomenti di geometria analitica delle lezioni precedenti. E’ in generale fondamentale ricordare la formula della distanza punto-retta ed inoltre avere dimestichezza con le relazioni di perpendicolarità e parallelismo tra rette. Ma tutto ciò è ampliamente disponibile qui su SìMatematica, con lezioni teoriche ed esercizi svolti. Per trovare gli argomenti di vostro interesse vi basterà utilizzare la comoda barra di ricerca interna. 😉
Come sempre, un saluto a tutti voi e buono studio con SìMatematica!
| « Lezione precedente | Esercizi correlati | Lezione successiva » |
| Ulteriori esercizi |
