Circonferenza

 - 

Circonferenza (scuole superiori)

La circonferenza è data dal luogo geometrico dei punti ciascuno dei quali presenta la stessa distanza da un fissato punto chiamato centro. Tale distanza si chiama raggio della circonferenza. Così sono punti di una circonferenza del piano di raggio r e centro C tutti i punti P tali da rispettare la condizione {\overline{PC} = r}.

In questa lezione studieremo insieme la circonferenza dal punto di vista della geometria analitica. In altre parole, vedremo come rappresentare una data circonferenza mediante un’equazione, e viceversa mostreremo come sotto determinate ipotesi ad un’equazione algebrica possa corrispondere geometricamente una circonferenza.

L’equazione che rappresenta una data circonferenza può in particolare essere scritta nella forma canonica, oppure nella forma con coordinate del centro e raggio. Questa seconda forma è quella più intuitiva, poiché effettivamente discende direttamente dalla definizione di circonferenza come luogo geometrico. Tuttavia, mostreremo tra pochi istanti come sia possibile passare agevolmente da una forma dell’equazione all’altra. E nello specifico, ci occuperemo del problema di ricavare dall’equazione canonica di una circonferenza le coordinate del suo centro e la misura del suo raggio.

Fatta la conoscenza delle equazioni della circonferenza, proseguiremo la lezione occupandoci dei problemi relativi all’intersezione di una circonferenza con una retta e alla ricerca della retta tangente ad una circonferenza in un suo dato punto. E in quest’ultimo caso, mostreremo l’utilizzo di più metodi risolutivi. Inoltre, con riferimento alle rette tangenti ad una circonferenza, sarà di nostro interesse anche il problema più generale relativo alla ricerca delle rette tangenti ad una circonferenza e tali da passare per una dato punto P esterno alla circonferenza stessa.

Nella parte finale della lezione ci occuperemo poi del problema della determinazione dell’equazione della circonferenza passante per tre punti non allineati.

Circonferenza come luogo geometrico

Un luogo geometrico di punti (o più brevemente luogo di punti) è un insieme di punti del piano cartesiano tali da rispettare una determinata condizione. In particolare, la circonferenza presenta la particolarità di essere costituita da punti tutti equidistanti da un comune punto {C} detto centro.

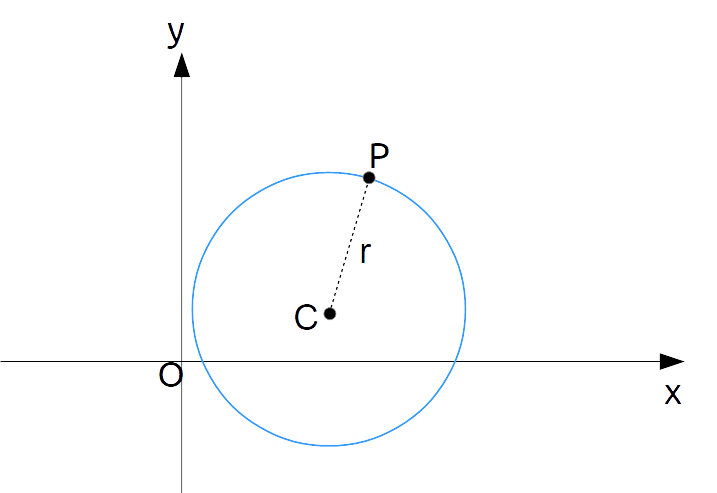
La circonferenza di centro {C} e raggio {r} è il luogo geometrico dei punti {P} del piano cartesiano {\pi} tali da avere la stessa distanza {r} rispetto al punto {C}. In simboli:{\mathscr{C}=\left\{ P \in \pi \: | \: \overline{CP} = r \right\}}

Ricordiamo che il simbolo {\overline{CP}} rappresenta la distanza nel piano tra i due punti {P} e {C}.

Una volta scelta una circonferenza, le coordinate del centro {C} sono note, e potremo indicarle ad esempio come segue:

C=\left( x_C, y_C\right)

ove {x_C} ed {y_C} sono numeri reali fissati.

Ora, il generico punto {P} appartenente alla circonferenza avrà coordinate:

P=(x,y)

Nell’ambito della definizione di circonferenza come luogo geometrico, a tali coordinate non si attribuiscono valori numerici, ma si lasciano piuttosto indicate. Ciò perché con il punto {P} indichiamo un generico punto appartenente alla circonferenza. Così le lettere {x} e {y} sono da intendersi come variabili o più propriamente come indeterminate.

Equazione di una circonferenza noti il centro e il raggio

Se disponiamo delle coordinate del centro e della misura del raggio, possiamo rappresentare la circonferenza mediante un’equazione di opportuna forma, che indicheremo come equazione della circonferenza noti il centro e il raggio.

Per la definizione di circonferenza come luogo geometrico, sappiamo che tutti i punti {P} appartenenti ad essa devono essere tali da rispettare la condizione:

\overline{CP}=r

Ma ricordando la formula della distanza tra due punti del piano cartesiano, tenendo conto di come abbiamo in precedenza indicato le coordinate dei punti {P} e {C} possiamo scrivere:

\sqrt{(x-x_C)^2+(y-y_C)^2}=r

ove al primo membro figura proprio la distanza tra i due punti {P} e {C}. E per definizione, tale distanza non potrà essere uguale che alla misura del raggio della circonferenza, ovvero {r} (vedi secondo membro dell’uguaglianza).

Quella che abbiamo appena scritto è un’equazione irrazionale. Tuttavia, in questo caso liberarci del simbolo di radice è piuttosto agevole. Basta infatti osservare prima di tutto che il raggio {r}, essendo una distanza, è per definizione sempre positivo. Di conseguenza, nell’elevare al quadrato entrambi i membri dell’equazione non dovremo imporre alcuna condizione di concordanza dei segni.

In secondo luogo, osserviamo che il radicando al primo membro (ovvero quanto contenuto all’interno della radice) è una somma di quadrati, e quindi sempre positivo. Di conseguenza, il radicale al primo membro avrà significato per valori delle coordinate del centro qualsiasi e per qualunque punto {P} considerato. Pertanto, non dovremo imporre alcuna condizione di realtà per il radicale al primo membro.

In conclusione, è possibile elevare tranquillamente al quadrato entrambi i membri dell’equazione senza alcuna discussione. Abbiamo:

(x-x_C)^2+(y-y_C)^2=r^2

e questa è l’equazione di una circonferenza noti il centro e il raggio.

L’equazione di una circonferenza noti il centro {C=(x_C, y_C)} e il raggio {r} si scrive come: {(x-x_C)^2+(y-y_C)^2=r^2}Viceversa, a partire da tale equazione è possibile risalire immediatamente alle coordinate del centro e alla misura del raggio della circonferenza.

Osservazione. L’equazione della circonferenza con centro l’origine si ottiene sostituendo alle coordinate {x_C} ed {y_C} il valore zero, ottenendo l’equazione:{x^2+y^2=r^2}

Esempio 1

Scrivere l’equazione della circonferenza con centro {C=(2,7)} e raggio {r=3}.

Sostituendo i valori delle coordinate del centro e del raggio nell’equazione della circonferenza noti il centro e il raggio:

(x-x_C)^2+(y-y_C)^2=r^2

otteniamo in maniera pressoché immediata l’equazione cercata:

(x-2)^2+(y-7)^2=9

Esempio 2

Scrivere l’equazione della circonferenza di centro {C=(3,-5)} e di raggio {r=4}.

Qui bisogna prestare attenzione al fatto che la coordinata {y_C} è negativa. Operiamo le sostituzioni con tutti i passaggi in modo da evitare spiacevoli errori di segno:

(x-3)^2+[y-(-5)]^2=4^2

Come possiamo vedere, occorre attenzione ai segni all’interno delle parentesi quadre. Ricordando le regole dell’algebra elementare abbiamo:

(x-3)^2+(y+5)^2=16

Esempio 3

Ricavare le coordinate del centro e la misura del raggio della circonferenza di equazione: {(x+2)^2+(y-7)^2=25}.

Ricordando che il secondo membro dell’equazione è il quadrato del raggio si ha:

r=\sqrt{25}=5

Quindi la misura del raggio è {5}.

Per quanto riguarda le coordinate del centro, osserviamo che l’equazione non è propriamente della forma:

(x-x_C)^2+(y-y_C)^2=r^2

Infatti, nella prima coppia di parentesi tonde dell’equazione in esame abbiamo una somma e non una differenza.

Così, al fine di evitare errori riscriviamo quanto contenuto all’interno della prima coppia di parentesi tonde sotto forma di un’equivalente differenza. In questo modo l’equazione di partenza diviene:

[\overbrace{x-(\underbrace{-2}_{x_C})}^{x+2=x-(-2)}]^2+(y-\underbrace{7}_{y_C})^2=25

Ora l’equazione è effettivamente nella forma generale ed è immediato risalire alle coordinate del centro:

C=(-2, 7)

Equazione di una circonferenza in forma canonica

Consideriamo l’equazione di una generica circonferenza noti il centro e il raggio:

(x-x_C)^2+(y-y_C)^2=r^2

Tale equazione consente di ricavare in modo praticamente diretto le coordinate del centro e il raggio. E tali dati individuano univocamente una circonferenza del piano cartesiano.

Allo stesso modo, l’equazione in forma esplicita di una retta, ovvero l’equazione:

y=mx+q, \qquad m, q \in \R

consente di ricavare immediatamente il coefficiente angolare e l’ordinata all’origine di una data retta del piano. E con tali dati una retta del piano è univocamente individuata.

Di conseguenza, l’equazione di una circonferenza noti il centro e il raggio e l’equazione in forma esplicita di una retta presentano una caratteristica in comune. In particolare, entrambe consentono di ricavare in modo diretto i dati che individuano univocamente il rispettivo ente geometrico da esse rappresentato.

Ora, abbiamo visto che una retta {r_1 } può anche essere rappresentata mediante l’equazione in forma implicita:

\small a_1x+b_1y+c_1=0, \qquad a_1,b_1,c_1 \in \R

con {a_1, b_1} mai contemporaneamente nulli.

Un’equazione di tale forma si caratterizza dalla presenza di un secondo membro nullo e dalla presenza di termini sommati tra loro al primo membro, senza che vi siano prodotti da eseguire. Così, l’idea è quella di ricercare un qualcosa di simile anche per la circonferenza. In altre parole, vogliamo ottenere per quest’ultima un’equazione che abbia in qualche modo una similitudine con l’equazione in forma implicita di una retta.

Allo scopo, poiché richiediamo un secondo membro nullo, il primo passo consiste nel trasportare il termine {r^2} dell’equazione della circonferenza al primo membro:

(x-x_C)^2+(y-y_C)^2-r^2=0

Inoltre, poiché non vogliamo prodotti lasciati da calcolare al primo membro, non ci resta che sviluppare i quadrati di binomi presenti:

x^2-2x_Cx+x_C^2+y^2-2y_Cy+y_C^2-r^2=0

Effettivamente ora già abbiamo un’equazione che ha qualcosa in comune con l’equazione in forma implicita di una retta {a_1x+b_1y+c_1=0}. Infatti, il secondo membro è nullo e al primo membro abbiamo soltanto somme algebriche di termini.

Proseguiamo ordinando i termini al primo membro come segue:

x^2+y^2-2x_Cx-2y_Cy+x_C^2+y_C^2-r^2=0

Poniamo per comodità a questo punto:

-2x_C=a; \quad -2y_C=b; \quad x_C^2+y_C^2-r^2=c \qquad (*)

Operando tali sostituzioni l’equazione diviene:

x^2+y^2+ax+by+c=0

Tale equazione rappresenta in generale, sotto le opportune ipotesi, l’equazione di una circonferenza in forma canonica.

Osserviamo che data una circonferenza di centro {C=(x_C, y_C)} e raggio {r}, è sempre possibile scriverne agevolmente l’equazione in forma canonica tenendo conto delle *, rilette in senso simmetrico:

a=-2x_C; \quad b=-2y_C; \quad c=x_C^2+y_C^2-r^2 

Viceversa, è anche possibile ricavare le coordinate del centro e la misura del raggio di una circonferenza a partire dalla sua (presunta) equazione in forma canonica. Infatti dalle * si ha, esplicitando le coordinate del centro e la misura del raggio:

\begin{align*} & x_C=-\dfrac{1}{2}a; \quad y_C=-\dfrac{1}{2}b; \\ \\ &r^2=x_C^2+y_C^2-c \quad \Rightarrow \quad r=\sqrt{x_C^2+y_C^2-c} \end{align*}

Tuttavia, ciò ha senso nei reali soltanto se il radicale {\sqrt{x_C^2+y_C^2-c}} esiste, e quindi se viene soddisfatta la condizione di realtà {{x_C^2+y_C^2-c} \geq 0} (quantità all’interno di una radice di indice pari positiva o al più nulla, vedi: radicali).

Inoltre, se il radicando {x_C^2+y_C^2-c} è nullo, la circonferenza ha raggio nullo e pertanto si riduce ad un punto (circonferenza degenere). Così l’equazione {x^2+y^2+ax+by+c=0} rappresenta una circonferenza reale non degenere se e solo se vale la condizione {x_C^2+y_C^2-c > 0}.

Osserviamo infine che la condizione appena scritta può essere agevolmente riespressa in funzione dei coefficienti {a,b,c}. Infatti, poiché si ha:

x_C=-\dfrac{1}{2}a; \quad y_C=-\dfrac{1}{2}b

la precedente diviene:

\left( -\dfrac{1}{2}a\right)^2+\left( -\dfrac{1}{2}b\right)^2-c > 0

ovvero:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0

Tra parentesi, in virtù di tali sostituzioni, se vale tale condizione è anche possibile esprimere il raggio direttamente in funzione dei coefficienti {a,b,c}:

r=\sqrt{x_C^2+y_C^2-c}=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}-c}

A questo punto possiamo fornire la definizione di equazione in forma canonica di una circonferenza.

L’equazione in forma canonica di una circonferenza si scrive come: {x^2+y^2+ax+by+c=0, \qquad a,b,c \in \R}Tale equazione rappresenta una circonferenza (reale non degenere) se e solo se vale la condizione:{\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0}Viceversa, a partire dalle coordinate del centro e dal raggio di una circonferenza, è sempre possibile scriverne l’equazione in forma canonica, osservando che si ha: {a=-2x_C; \quad b=-2y_C; \quad c=x_C^2+y_C^2-r^2}In altre parole, è sempre possibile calcolare i coefficienti {a, b, c} necessari a scrivere l’equazione di una circonferenza in forma canonica partendo dalle coordinate del suo centro e dalla misura del suo raggio. Infatti, le espressioni appena scritte per i coefficienti {a,b,c} sono definite in tutto {\R}.

Nota: con il termine “circonferenza reale non degenere” intendiamo che la misura del suo raggio è data da un numero reale (ovviamente positivo) e non nullo. Se il raggio di una circonferenza è nullo, questa si dice “degenere” poiché si riduce ad un punto.

Attenzione. Se abbiamo un’equazione della circonferenza in forma non propriamente canonica, ovvero un’equazione del tipo{Ax^2+Ay^2+Cx+Dy+E=0} con {A} diverso da {1}, è necessario prima di cominciare a lavorare sull’equazione ridurla alla forma canonica, dividendo tutti i termini per {A}.

Osservazione. Se nell’equazione di una circonferenza in forma canonica il termine {c} è nullo, allora la circonferenza è passante per l’origine. In altre parole, l’origine appartiene alla circonferenza. Ciò si verifica immediatamente sostituendo le coordinate dell’origine all’equazione in forma canonica della circonferenza:{0^2+0^2+a \cdot 0 + b \cdot 0 +c = 0 \quad \Rightarrow \quad c=0}

Ora vediamo degli esercizi di esempio relativi all’equazione in forma canonica, ed inoltre vediamo come ricavare le coordinate del centro e la misura del raggio a partire dall’equazione in forma canonica.

Esempio 4

Scrivere l’equazione in forma canonica della circonferenza di centro {C=(-2, -7)} e raggio {r=3}.

Essendo note le coordinate {x_C} ed {y_C} del centro e il raggio {r} della circonferenza, possiamo ricavare agevolmente i coefficienti {a,b,c} relativi all’equazione in forma canonica grazie alle relazioni *. Cominciamo ricavando i coefficienti {a} e {b}:

a=-2x_C=-2 \cdot (-2)=4; \qquad b=-2y_C=-2 (-7)=14

Per il coefficiente {c} abbiamo inoltre:

c=x_C^2+y_C^2-r^2=(-2)^2+(-7)^2-3^2=4+49-9=44

A questo punto non resta che sostituire i valori dei coefficienti {a,b,c} appena trovati nell’espressione generale dell’equazione di una circonferenza in forma canonica:

x^2+y^2+ax+by+c=0

Otteniamo:

x^2+y^2+4x+14y+44=0

E questa è l’equazione in forma canonica cercata.

Esempio 5

Verificare che l’equazione: {x^2+y^2+5x-7y+3=0}rappresenta una circonferenza (reale non degenere) e quindi calcolare le coordinate del centro e la misura del raggio.

Cominciamo verificando la condizione:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0

Si ha nel nostro caso:

\dfrac{5^2}{4}+\dfrac{(-7)^2}{4}-3 > 0

ovvero:

\dfrac{25}{4}+\dfrac{49}{4}-3 > 0 \quad \Rightarrow \quad \dfrac{31}{2}> 0

Poiché la disuguaglianza numerica alla quale siamo pervenuti è vera, la condizione è verificata.

Quindi siamo in presenza di una circonferenza reale non degenere e possiamo procedere a calcolare le coordinate del suo centro e la misura del suo raggio.

Per calcolare le coordinate del centro utilizziamo le formule:

x_C=-\dfrac{1}{2}a; \qquad y_C=-\dfrac{1}{2}b

dalle quali otteniamo per il nostro caso:

x_C=-\dfrac{1}{2} \cdot 5=-\dfrac{5}{2}; \qquad y_C=-\dfrac{1}{2} \cdot(-7)=\dfrac{7}{2}

Così la circonferenza in esame ha come centro il punto {C=\left( -\dfrac{5}{2}, \dfrac{7}{2}\right)}.

Per il raggio abbiamo infine:

\begin{align*} & r=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}-c}=\sqrt{\dfrac{5^2}{4}+\dfrac{(-7)^2}{4}-3}=  \\ \\ & =\sqrt{\dfrac{25}{4}+\dfrac{49}{4}-3}=\sqrt{\dfrac{25+49-12}{4}}=\sqrt{\dfrac{62}{4}}=\sqrt{\dfrac{31}{2}}=\\ \\ & =\dfrac{\sqrt{31}}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{\sqrt{31} \cdot \sqrt{2}}{2}=\dfrac{\sqrt{31 \cdot 2}}{2}=\dfrac{\sqrt{62}}{2}\end{align*}

Quindi in conclusione l’equazione in forma canonica di partenza rappresenta la circonferenza di centro {C=\left( -\dfrac{5}{2}, \dfrac{7}{2}\right)} e raggio {r=\dfrac{\sqrt{62}}{2}}.

Esempio 6

Verificare se l’equazione {x^2+y^2+2x+3y+100=0}rappresenta o meno una circonferenza reale.

Controlliamo se è verificata nel nostro caso la condizione:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0

Abbiamo:

\dfrac{2^2}{4}+\dfrac{3^2}{4}-100 > 0

ovvero:

1+\dfrac{9}{4}-100 > 0 \quad \Rightarrow \quad -\dfrac{387}{4} > 0 \quad \text{falso}

Poiché otteniamo una disuguaglianza numerica falsa, la condizione non è verificata. Di conseguenza, all’equazione data non corrisponde alcuna circonferenza reale.

Esempio 7

Determinare centro e raggio della circonferenza di equazione {4x^2+4y^2-8x+3y=0}.

L’equazione non è propriamente in forma canonica, in quanto i coefficienti dei termini in {x^2} e {y^2} sono diversi da {1}. Manca anche il termine noto, ma ciò non è un problema poiché il termine noto {c} può assumere un qualunque valore reale, anche compreso lo zero. E in particolare, come visto in una precedente osservazione, essendo {c=0} la circonferenza è passante per l’origine.

Cominciamo allora anzitutto riconducendo l’equazione alla forma canonica, dividendo tutti i termini per {4}:

\dfrac{4}{4}x^2+\dfrac{4}{4}y^2-\dfrac{8}{4}x+\dfrac{3}{4}y=0

e quindi:

x^2+y^2-2x+\dfrac{3}{4}y=0

Ora l’equazione è in forma canonica e possiamo determinare centro e raggio con le formule ormai note (omettiamo per brevità i passaggi):

C=\left(1, -\dfrac{3}{8} \right); \qquad r=\dfrac{\sqrt{73}}{8}

Come passare dall’equazione noti centro e raggio all’equazione canonica e viceversa

Come immediata conseguenza delle procedure viste negli esempi precedenti, è sempre possibile passare dall’equazione di una circonferenza noti centro e raggio all’equazione in forma canonica. Infatti, basta calcolare i coefficienti {a,b,c} a partire dalle coordinate del centro e dalla misura del raggio, quindi sostituire i valori ottenuti nell’equazione in forma canonica {x^2+y^2+ax+by+c=0}.

Viceversa, se siamo in presenza di una circonferenza reale è anche possibile passare dalla equazione in forma canonica all’equazione con centro e raggio noti. Basterà infatti ricavare coordinate del centro e misura del raggio a partire dai coefficienti {a,b,c}, per poi sostituire i valori ottenuti nell’equazione con centro e raggio noti {(x-x_C)^2+(y-y_C)^2=r^2}.

Vediamo brevemente un paio di esempi, anche se comunque le tecniche da utilizzare sono del tutto simili a quelle sin qui mostrate.

Esempio 8

Riscrivere l’equazione della circonferenza noti centro e raggio seguente in forma canonica:{(x-5)^2+(y+9)^2=81}.

Anzitutto abbiamo:

C=\left( 5,-9\right); \qquad r=\sqrt{81}=9

Per l’ordinata del centro attenzione al segno. 😉

Proseguiamo a questo punto ricavando i coefficienti {a,b,c} per l’equazione in forma canonica, utilizzando le coordinate del centro e la misura del raggio appena determinati:

\begin{align*} & a=-2x_C=-2 \cdot 5 = -10; \qquad b=-2 y_C=-2 \cdot (-9)=18; \\ \\ & c=x_C^2+y_C^2-r^2=(5)^2+(-9)^2-9^2=25+81-81=25\end{align*}

Di conseguenza sostituendo i valori dei coefficienti {a,b,c} appena calcolati nell’equazione canonica della circonferenza {x^2+y^2+ax+by+c=0} otteniamo:

x^2+y^2-10x+18y+25=0

e questa è in conclusione l’equazione in forma canonica della circonferenza in esame.

Esempio 9

Riesprimere nella forma con centro e raggio noti la seguente equazione canonica di una circonferenza:{x^2+y^2-4x-2y-4=0}

Il testo già ci dice che si tratta di una circonferenza (reale non degenere), per cui omettiamo la corrispondente verifica. In ogni caso, lo ricordiamo ancora, si tratterebbe soltanto di verificare la condizione:

\dfrac{a^2}{4}+\dfrac{b^2}{4}-c > 0

Proseguiamo piuttosto calcolando le coordinate del centro e la misura del raggio a partire dai coefficienti {a,b,c}, che nel nostro caso sono:

a=-4; \quad b=-2; \quad c=-4

Abbiamo:

\begin{align*} &x_C=-\dfrac{1}{2}a=-\dfrac{1}{2} \cdot(-4)=2; \quad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2} \cdot (-2)=1; \\ \\ & r=\sqrt{\dfrac{a^2}{4}+\dfrac{b^2}{4}-c}=\sqrt{\dfrac{(-4)^2}{4}+\dfrac{(-2)^2}{4}-(-4)}=\\ \\ & =\sqrt{\dfrac{16}{4}+\dfrac{4}{4}+4}=\sqrt{\dfrac{16+4+16}{4}}=\sqrt{\dfrac{36}{4}}=\dfrac{6}{2}=3\end{align*}

Non resta a questo punto che sostituire i valori trovati nell’equazione:

(x-x_C)^2+(y-y_C)^2=r^2

ottenendo in conclusione:

(x-2)^2+(y-1)^2=9

Metodo del completamento dei quadrati per ricavare centro e raggio dall’equazione canonica

Oltre all’utilizzo delle formule sin qui viste, per ricavare centro e raggio di una circonferenza a partire dalla sua equazione canonica esiste anche un altro metodo, noto come metodo del completamento dei quadrati. Tale procedura consente evidentemente anche di passare dall’equazione in forma canonica di una circonferenza a quella con centro e raggio noti. Infatti, una volta ricavate le coordinate del centro e la misura del raggio di una circonferenza è immediato scriverne l’equazione nella forma {(x-x_C)^2+(y-y_C)^2=r^2}.

Per illustrare il metodo del completamento dei quadrati (già visto a suo tempo nell’ambito dei polinomi) partiamo subito da un esempio pratico. Riscriviamo nella forma con centro e raggio noti l’equazione in forma canonica data nell’esempio precedente:

x^2+y^2-4x-2y-4=0

L’idea è quella di ricondurre il primo membro dell’equazione ad una somma di quadrati, e di avere inoltre al secondo membro un solo numero. Cominciamo allora trasportando anzitutto il termine noto al secondo membro:

x^2+y^2-4x-2y=4

Adesso, riordiniamo i termini al primo membro in modo da avere le lettere uguali tra loro una di seguito all’altra:

x^2-4x+y^2-2y=4 \qquad (**)

Ora, i binomi {x^2-4x} e {y^2-2y} possono essere visti come dei quadrati incompleti. Infatti, in ciascun binomio abbiamo il quadrato di un termine e il doppio prodotto. Cominciamo completando il primo binomio:

x^2-4x+\boxed{4}

Il polinomio appena scritto è un quadrato. Infatti si ha {(x-2)^2=x^2-4x+4}. In generale, per individuare il numero necessario a completare il quadrato basta guardare con attenzione al termine che rappresenta il doppio prodotto. Nel nostro caso:

-4x=2 \cdot (-2) \cdot x

Così abbiamo il doppio prodotto tra i termini {-2} e {x}. Nel quadrato da completare figura già il quadrato di {x} (infatti è già presente il termine {x^2}). Di conseguenza, il termine mancante per completare il quadrato è {4}, cioè il quadrato di {-2}.

Allo stesso modo, per il secondo binomio:

y^2-2y+\boxed{1}

Infatti si ha {(y-1)^2=y^2-2y+1}, e quindi aggiungendo il termine {1} abbiamo anche in questo caso ottenuto un quadrato.

Ora, nell’equazione ** possiamo sostituire ai quadrati incompleti i quadrati completi appena scritti, ma a patto di tenere conto del primo principio di equivalenza delle equazioni. In particolare, dobbiamo sommare al secondo membro le quantità aggiunte ai binomi di partenza. Così in pratica dovremo sommare anche al secondo membro i numeri evidenziati nei riquadri. Abbiamo quindi:

x^2-4x+\boxed{4}+y^2-2y+\boxed{1}=4+\boxed{4+1}

A questo punto sostituiamo al posto dei due polinomi al secondo membro i corrispondenti quadrati di binomi. Eseguiamo inoltre la somma al secondo membro:

(x-2)^2+(y-1)^2=9

Ci ritroviamo ora con l’equazione della circonferenza in esame nella forma con centro e raggio noti. E’ dunque immediato a questo punto ricavare le coordinate del centro e la misura del raggio della circonferenza:

C=(2, 1); \qquad r=\sqrt{9}=3

Ritroviamo così i risultati già ottenuti con il metodo precedente.

Anche per questo metodo, una precisazione importante. Nel caso in cui i coefficienti dei termini in {x^2} e {y^2} dell’equazione data in partenza siano diversi da {1}, occorre prima ricondurre l’equazione alla forma canonica, e soltanto a quel punto procedere con il metodo del completamento dei quadrati. Diversamente, il metodo è comunque applicabile ma risulta più complicato.

Ad esempio, proviamo a determinare centro e raggio della circonferenza reale di equazione:

2x^2+2y^2-12x+16y-31=0

Cominciamo anzitutto dividendo tutti i termini per {2} (il coefficiente in comune ai termini in {x^2} e {y^2}):

x^2+y^2-6x+8y-\dfrac{31}{2}=0

Riordiniamo opportunamente i termini:

x^2-6x+y^2+8y=\dfrac{31}{2}

Ora completiamo i quadrati non dimenticando di “bilanciare” il secondo membro:

x^2-6x+\boxed{9}+y^2+8y+\boxed{16}=\dfrac{31}{2}+\boxed{9+16}

e quindi:

(x-3)^2+(y+4)^2=\dfrac{81}{2}

da cui abbiamo in conclusione:

C=(3, -4); \qquad r=\dfrac{9}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}}=\dfrac{9\sqrt{2}}{2}

Il metodo del completamento dei quadrati applicato alla circonferenza presenta indubbiamente un chiaro vantaggio. Infatti, esso consente di risalire a centro e raggio di una circonferenza a partire dalla sua equazione canonica senza dover ricordare alcuna formula specifica. Tuttavia, lo svantaggio è dato dal dover avere una certa dimestichezza con i quadrati dei binomi, ed in particolare la procedura di completamento dei quadrati può non essere in generale del tutto immediata. Di conseguenza, consigliamo comunque di studiare con cura le formule mostrate in precedenza per calcolare centro e raggio a partire dall’equazione canonica. Come sempre, il consiglio è soprattutto quello di regolarvi in base alle indicazioni del vostro insegnante.

Ricerca dei punti di intersezione tra una circonferenza ed una retta

Proseguiamo lo studio della circonferenza con il problema della ricerca delle coordinate degli eventuali punti di intersezione tra una circonferenza ed una retta del piano.

Indichiamo con {\gamma} una circonferenza avente equazione data in forma canonica:

\gamma: x^2+y^2+ax+by+c=0

Indichiamo inoltre con {r_1} una retta con equazione data in forma implicita:

r_1: a_1x+b_1y+c_1=0

Il nostro obiettivo è determinare gli eventuali punti di intersezione tra la circonferenza {\gamma} e la retta {r_1}. In termini più formali, ciò che desideriamo è determinare gli eventuali punti appartenenti all’insieme {\gamma \cap r_1}, ovvero l’insieme di punti che si ottiene dall’intersezione fra l’insieme di punti {\gamma} e l’insieme di punti {r_1} (una circonferenza e una retta possono essere riguardate come un luogo di punti o insieme di punti).

In modo del tutto simile a quanto visto sull’intersezione tra rette, le coordinate degli eventuali punti di intersezione tra {\gamma} e {r_1} si ottengono risolvendo il seguente sistema, nel quale figurano le equazioni della circonferenza e retta considerate:

\begin{cases}\gamma: x^2+y^2+ax+by+c=0 \\ \\  r_1: a_1x+b_1y+c_1=0 \end{cases}

Il sistema dato è non lineare (vedi sistemi non lineari). In questo caso, la tecnica da utilizzare è data dall’esplicitare una delle due variabili dalla seconda equazione, e quindi sostituire l’espressione ottenuta nella prima equazione. In tal modo, la prima equazione si ridurrà ad un’equazione di secondo grado in una sola incognita, che potremo risolvere. Se l’equazione di secondo grado fornirà due soluzioni reali e distinte, potremo sostituire i valori ottenuti nella seconda equazione a sistema (l’equazione della retta), in modo da ottenere in conclusione le coordinate dei due punti di intersezione tra la circonferenza e la retta.

Nel caso in cui invece l’equazione di secondo grado dovesse fornire due soluzioni reali e coincidenti, otterremo un unico punto di intersezione tra la circonferenza e la retta considerate. In tal caso, diremo che la retta è tangente alla circonferenza in quel punto.

Infine, se l’equazione di secondo grado non dovesse avere soluzioni reali, la conclusione che dovremo trarre è che non esiste alcun punto di intersezione tra la circonferenza e la retta in esame.

Ma vediamo subito la tecnica da utilizzare mediante un esempio pratico. Proviamo a calcolare le coordinate degli eventuali punti di intersezione tra la circonferenza {\gamma: x^2+y^2-3x-\dfrac{7}{2}y=0} e la retta {r_1: 2x+y-6=0}.

In casi di questo tipo, l’equazione della circonferenza deve essere in forma canonica, mentre l’equazione della retta deve essere in forma esplicita. Quest’ultimo accorgimento consente infatti di esplicitare una variabile dall’equazione della retta. D’altro canto, la forma canonica dell’equazione della circonferenza consente di ricondurci agevolmente, una volta effettuata l’opportuna sostituzione, all’equazione di secondo grado risolvente.

Nel nostro caso l’equazione della circonferenza è già in forma canonica, mentre dobbiamo ricondurre alla forma esplicita l’equazione della retta. Abbiamo, impostando il sistema:

\small \begin{cases} \gamma: x^2+y^2-3x-\dfrac{7}{2}y=0 \\ \\ r_1: 2x+y-6=0\end{cases} \quad \Rightarrow \quad \begin{cases} \gamma: x^2+y^2-3x-\dfrac{7}{2}y=0 \\ \\ r_1: y=\boxed{-2x+6}\end{cases}

Ora procediamo sostituendo nella prima equazione l’espressione appena ottenuta per {y}:

\begin{cases}x^2+(-2x+6)^2-3x-\dfrac{7}{2}(-2x+6)=0 \\ \\ y=-2x+6 \end{cases}

A questo punto concentriamoci sulla prima equazione a sistema. Sviluppiamo in particolare tutti i calcoli in essa presenti:

x^2+4x^2-24x+36-3x+7x-21=0

da cui, sommando i termini simili:

5x^2-20x+15=0 \quad \Rightarrow \quad x^2-4x+3=0

Ora si tratta di risolvere l’equazione di secondo grado ottenuta:

x_{1,2}= \dfrac{4 \pm \sqrt{(-4)^2-4 \cdot 1 \cdot 3}}{2 \cdot 1}=\dfrac{4 \pm 2}{2}=\begin{cases} 3 \\ \\ 1\end{cases}

Poiché siamo pervenuti a due soluzioni reali e distinte, possiamo procedere sostituendo i valori della {x} ottenuti nella seconda equazione a sistema, ovvero nell’equazione {y=-2x+6} relativa alla retta {r_1}. Abbiamo:

\begin{align*} &y=-2x+6 \quad \text{con}  \: x_1=3 \quad \Rightarrow \quad y_1=0 \\ \\ & y=-2x+6 \quad \text{con} \: x_2=1 \quad \Rightarrow \quad y_2=4\quad \end{align*}

Abbiamo così calcolato le coordinate {x_1, y_1} ed {x_2, y_2} relative ai punti di intersezione tra la circonferenza e la retta date. In particolare, indicando tali punti di intersezione con {A} e {B} si ha in conclusione:

A=(3,0), \quad B=(1,4)

Come determinare l’equazione della retta tangente ad una circonferenza in un suo punto

Passiamo ora al problema relativo a come determinare l’equazione della retta tangente ad una circonferenza in un dato punto della circonferenza stessa.

Consideriamo la seguente figura, nella quale abbiamo una retta {t} tangente nel punto {P} ad una circonferenza di equazione nota e di centro {C}:

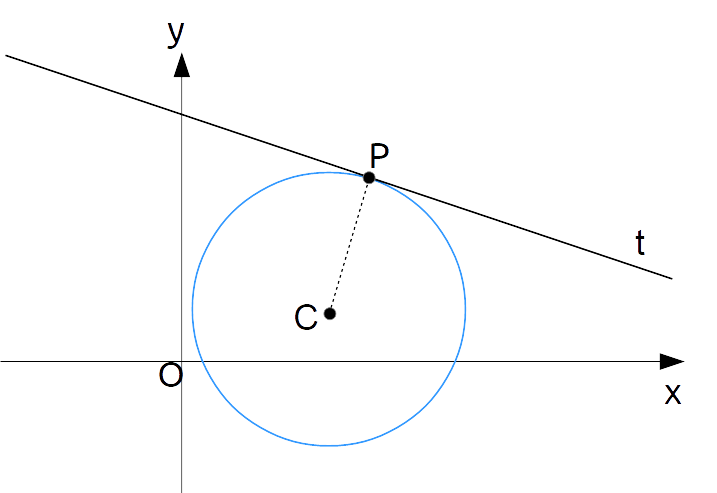
Osserviamo che la retta {t} passa per il punto {P=(x_P, y_P)} di coordinate anch’esse note. Di conseguenza, è possibile esprimere l’equazione della retta {t} come:

t: y-y_P=m(x-x_P) \qquad (@)

Abbiamo qui utilizzato la formula per l’equazione di una retta noti il coefficiente angolare ed un punto ad essa appartenente.

Nel nostro caso, tuttavia, il coefficiente angolare {m} è al momento ignoto. Ma, poiché l’equazione della circonferenza è nota, è possibile risalire alle coordinate {x_C} e {y_C} del suo centro. Ora, la retta passante per i punti {C} e {P} è per proprietà geometriche elementari perpendicolare alla retta tangente {t}. E dato che le coordinate dei punti {P} e {C} sono note, è possibile intanto calcolare il coefficiente angolare {m_{CP}} della retta passante per tali punti:

m_{CP}=\dfrac{y_P-y_C}{x_P-x_C}

Ma a questo punto il coefficiente angolare della retta {t}, perpendicolare alla retta passante per i punti {C} e {P}, sarà l’inverso del reciproco di {m_{CP}} (vedi: rette perpendicolari):

m=-\dfrac{1}{m_{CP}}

Ed essendo ormai noto il valore di {m}, sostituendolo nella @ è possibile scrivere in conclusione l’equazione della retta tangente alla circonferenza nel punto {P}.

Esempio 10

Determinare l’equazione della retta {t} tangente alla circonferenza {\gamma: x^2+y^2+2x-5y+3=0} nel punto {P=(1,2)}.

Cominciamo verificando la condizione di appartenenza del punto alla circonferenza. Per farlo, basta sostituire le sue coordinate nell’equazione della circonferenza stessa. Abbiamo:

1^2+2^2+2 \cdot 1 - 5 \cdot 2 +3 = 0 \quad \Rightarrow \quad  0 = 0 \qquad \text{OK}

Quindi il punto {P} appartiene alla circonferenza. Di conseguenza, la retta passante per il centro della circonferenza e per il punto {P} è perpendicolare alla retta tangente {t}. E’ dunque possibile utilizzare il metodo risolutivo che sfrutta proprio tale relazione di perpendicolarità.

Determiniamo il centro della circonferenza data:

x_C=-\dfrac{1}{2}a=-\dfrac{1}{2}\cdot2=-1; \qquad y_C=-\dfrac{1}{2}b=-\dfrac{1}{2}(-5)=\dfrac{5}{2}

Essendo anche note le coordinate del punto {P}, possiamo calcolare il coefficiente angolare {m_{CP}} della retta passante per {C} e {P}:

m_{CP}=\dfrac{y_P-y_C}{x_P-x_C}=\dfrac{2-\dfrac{5}{2}}{1-(-1)}=-\dfrac{1}{2} \cdot \dfrac{1}{2}=-\dfrac{1}{4}

E quindi per il coefficiente angolare della retta {t} abbiamo:

m=-\dfrac{1}{m_{CP}}=-\dfrac{1}{-\frac{1}{4}}=4

Così in conclusione utilizzando la @ possiamo scrivere l’equazione della tangente alla circonferenza nel punto {P}:

y-y_P=m (x-x_P) \quad \Rightarrow y-2=4(x-1)

Sviluppando i calcoli abbiamo in definitiva:

t:y=4x-2

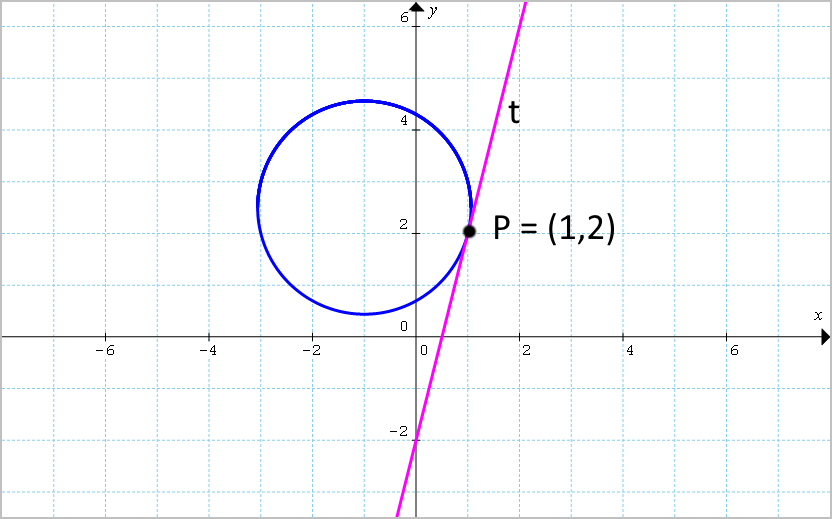
Vediamo ora un altro metodo per poter determinare l’equazione della retta tangente ad una circonferenza in un punto appartenente ad essa, basato sull’uso delle opportune formule di sdoppiamento.

Formule di sdoppiamento per la circonferenza

In alternativa all’utilizzo della relazione di perpendicolarità fra rette, si può ricorrere alle formule di sdoppiamento per la circonferenza.

Supponiamo ancora di voler determinare l’equazione della retta {t} tangente ad una data circonferenza in un punto {P} appartenente alla circonferenza stessa. Sia data l’equazione in forma canonica della circonferenza:

\gamma:x^2+y^2+ax+by+c=0

E’ possibile ottenere l’equazione della retta {t} a partire dall’equazione in forma canonica della circonferenza operando nell’equazione della circonferenza stessa le seguenti sostituzioni (formule di sdoppiamento per la circonferenza):

x^2 \rightarrow x_P \cdot x; \quad y^2 \rightarrow   y_P \cdot y; \quad x \rightarrow \dfrac{x+x_C}{2}; \quad y \rightarrow \dfrac{y+y_C}{2}

In altre parole, nell’equazione della circonferenza assegnata dobbiamo sostituire ad {x^2} la quantità {x_P \cdot x}, ad {y^2} la quantità {y_P \cdot y} e così via.

Con tali sostituzioni, abbastanza semplici da ricordare, l’equazione canonica della circonferenza data diviene:

x_Px+y_Py+a\dfrac{x+x_C}{2}+b\dfrac{y+y_C}{2}+c=0

In tal modo ci riconduciamo ad un’equazione di primo grado nelle incognite {x} ed {y} che effettivamente corrisponde alla retta tangente alla circonferenza in esame nel suo punto {P}.

Riprendiamo a questo punto l’esempio precedente e vediamo di risolverlo con questo metodo alternativo.

L’obiettivo era determinare l’equazione della retta tangente alla circonferenza {\gamma: x^2+y^2+2x-5y+3=0} nel suo punto {P=(1,2)}.

Tenendo conto dei valori delle coordinate del punto {P}, si ha {x_P=1} e {y_P=2}. Di conseguenza, le formule di sdoppiamento divengono nel nostro caso:

x^2 \rightarrow 1 \cdot x; \quad y^2\rightarrow 2 \cdot y; \quad x \rightarrow \dfrac{x+1}{2}; \quad y\rightarrow \dfrac{y+2}{2}

Così operando tali sostituzioni nell’equazione canonica della circonferenza in esame otteniamo:

x+2y+2 \cdot \left( \dfrac{x+1}{2}\right)-5 \cdot \left( \dfrac{y+2}{2}\right)+3=0

la quale eseguendo gli opportuni calcoli porta all’equazione della retta {t} cercata:

\begin{align*} &x+2y+x+1-\dfrac{5}{2}y-5+3=0; \\ \\ &\dfrac{1}{2}y=2x-1; \\ \\ & t: y=4x-2\end{align*}

Effettivamente ritroviamo l’equazione già determinata con il metodo precedente.

Equazioni delle rette tangenti alla circonferenza passanti per un punto esterno alla circonferenza stessa

Fissato un punto {P} esterno ad una data circonferenza, è sempre possibile determinare le equazioni delle due rette tangenti alla circonferenza stessa e passanti per quello stesso punto {P}. Sottolineiamo fin da subito il fatto che, diversamente dal caso esaminato in precedenza (ove il punto {P} apparteneva alla circonferenza), se il punto {P} è esterno alla circonferenza non dobbiamo determinare una sola equazione, ma due, poiché due sono le rette tangenti alla circonferenza stessa.

Il metodo più generale si basa sull’impostare un sistema risolvente, in una maniera abbastanza simile a quella con la quale abbiamo determinato le coordinate dei punti di intersezione tra una circonferenza ed una retta del piano.

Tuttavia, tale metodo è abbastanza scomodo poiché porta nei casi generali a calcoli piuttosto lunghi. Vedremo comunque nel seguito come utilizzare tale metodo.

Una tecnica meno scomoda per la determinazione delle equazioni delle rette tangenti ad una circonferenza passanti per un dato punto esterno ad essa si basa sulla formula della distanza punto-retta. Consideriamo la seguente figura:

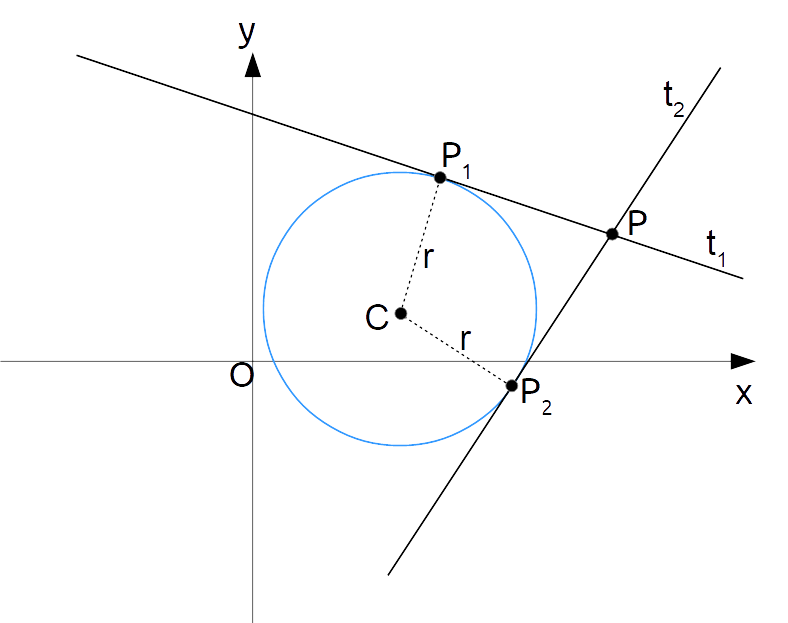
Le rette {t_1} e {t_2} sono tangenti alla circonferenza nei punti {P_1} e {P_2} ed inoltre passano per il punto {P} esterno ad essa.

Ora, è fondamentale osservare che entrambe le rette {t_1} e {t_2} hanno una distanza rispetto al centro {C} della circonferenza uguale al raggio della circonferenza stessa. Così, nel ricercare le equazioni delle rette tangenti alla circonferenza passanti per {P}, dovremo proprio imporre tale condizione.

Importante. Nel caso particolare in cui una delle due rette tangenti sia verticale, nell’applicare i metodi nel seguito illustrati otterremmo l’equazione di una sola retta tangente. Tuttavia, le rette tangenti ad una circonferenza e passanti per un punto {P} esterno alla circonferenza stessa sono sempre due. Così, in tal caso, l’equazione mancante sarà quella relativa alla retta verticale passante per il punto {P}. Ci occuperemo nel dettaglio di questo aspetto in una prossima lezione.

Vediamo subito un esempio.

Esempio (equazioni delle rette tangenti ad una circonferenza passanti per un punto ad essa esterno, con l’utilizzo della formula della distanza tra un punto ed una retta nel piano)

Scrivere le equazioni delle rette tangenti alla circonferenza reale {\gamma: x^2+y^2+3x+4y-7=0 } e passanti per il punto esterno alla circonferenza {P=(4,3)}.

Osserviamo che entrambe le rette tangenti dovranno necessariamente appartenere al punto {P=(4,3)}. Per cui utilizzando l’equazione di una retta per un punto con coefficiente angolare noto potremo intanto esprimere le equazioni delle rette tangenti cercate come segue:

t_1: y-y_P=m_1(x-x_P); \qquad t_2: y-y_P=m_2(x-x_P)

ove {x_P} ed {y_P} sono le coordinate del punto {P}.

Sostituendo le coordinate del punto {P} note si ottiene rispettivamente:

t_1: y-3=m_1(x-4); \qquad t_2: y-3=m_2(x-4)

Indichiamo per semplicità una qualunque delle due equazioni delle rette {t_1} e {t_2} con:

y-3=m(x-4)

intendendo con {m} il coefficiente angolare di una delle due rette tangenti.

Osserviamo che per l’ordinata all’origine si ha:

y=mx+(-4m+3) \quad \Rightarrow \quad q=-4m+3

Determiniamo le coordinate del centro della circonferenza:

x_C=-\dfrac{1}{2}a=-\dfrac{1}{2}\cdot3=-\dfrac{3}{2}; \qquad y_C=-\dfrac{1}{2}\cdot b=-\dfrac{1}{2}\cdot 4=-2

ed il raggio:

r=\sqrt{x_C^2+y_C^2-c}=\sqrt{\left( -\dfrac{3}{2}\right)^2+(-2)^2-(-7)}=\dfrac{\sqrt{53}}{2}

Imponiamo a questo punto la condizione che la distanza fra tali rette tangenti e il centro della circonferenza sia uguale al raggio. Stiamo attenti ad usare la formula della distanza punto-retta nella forma che utilizza come dati il coefficiente angolare e l’ordinata all’origine della retta:

\underbrace{\dfrac{|y_C-(mx_C+q)|}{\sqrt{1+m^2}}}_{d(P, C)}=\underbrace{\dfrac{\sqrt{53}}{2}}_{r}

Sostituendo anche le coordinate del centro della circonferenza e l’ordinata all’origine {q} come la funzione di {m} precedentemente calcolata, otteniamo un’equazione di secondo grado nella sola incognita {m}:

\dfrac{\left|-2-\left[ m \cdot \left( -\dfrac{3}{2}\right)-4m+3\right]\right|}{\sqrt{1+m^2}}=\dfrac{\sqrt{53}}{2}

Risolviamo l’equazione rispetto ad {m}:

\begin{align*} &\dfrac{\left| -2-\left( -\dfrac{3}{2}m-4m+3\right)\right|}{\sqrt{1+m^2}}=\dfrac{\sqrt{53}}{2}; \\ \\ & \dfrac{\left|-2+\dfrac{3}{2}m+4m-3\right|}{\sqrt{1+m^2}}=\dfrac{\sqrt{53}}{2}; \\ \\ & \dfrac{\left|\dfrac{11}{2}m-5 \right|}{\sqrt{1+m^2}}=\dfrac{\sqrt{53}}{2};\\ \\ & \dfrac{\left|\dfrac{11}{2}m-5 \right|}{\sqrt{1+m^2}}-\dfrac{\sqrt{53}}{2}=0; \\ \\ & \dfrac{2 \cdot \left|\dfrac{11}{2}m-5 \right|-\sqrt{53} \cdot \sqrt{1+m^2}}{\cancel{2\sqrt{1+m^2}}}=0; \\ \\ &|11m-10|-\sqrt{53(1+m^2)}=0; \\ \\ & |11m-10|=\sqrt{53(1+m^2)}; \\ \\ & (11m-10)^2=53(1+m^2); \\ \\ & 121m^2+100-220m-53-53m^2=0;\\ \\ & 68m^2-220m+47=0\end{align*}

Per meglio comprendere i passaggi osserviamo che abbiamo potuto eliminare il denominatore {2\sqrt{1+m^2}} senza alcuna discussione. Infatti, si tratta di una quantità mai nulla. Inoltre, nei passaggi successivi è stato possibile eliminare il simbolo di radice elevando entrambi i membri dell’equazione al quadrato. Anche ciò non richiede in questo caso alcuna discussione, poiché nell’equazione {|11m-10|=\sqrt{53(1+m^2)}} entrambi i membri (un valore assoluto ed una radice quadrata) sono sempre positivi (quindi non serve alcuna condizione di concordanza del segno).

A questo punto risolvendo l’equazione di secondo grado nell’incognita {m} si ottiene (vedi: formula risolutiva ridotta):

\begin{align*} &m_{1,2}=\dfrac{110 \pm \sqrt{(-110)^2-68 \cdot 47}}{68}=\dfrac{110 \pm \sqrt{12100-3196}}{68}=\\ \\ & =\dfrac{110 \pm \sqrt{8904}}{68}=\dfrac{110\pm 2\sqrt{2226}}{68}=\dfrac{2\left(55\pm \sqrt{2226}\right)}{68}=\\ \\ & =\dfrac{1}{34} \cdot \left( 55 \pm \sqrt{2226}\right)=\begin{cases} \dfrac{1}{34} \cdot \left( 55 + \sqrt{2226}\right) \\ \\ \dfrac{1}{34} \cdot \left( 55-\sqrt{2226}\right)\end{cases} \end{align*}

Abbiamo così ottenuto i due coefficienti angolari {m_1} ed {m_2} relativi alle rette tangenti che stiamo cercando. Di conseguenza, sostituendo i valori trovati nelle:

t_1: y-3=m_1(x-4); \qquad t_2: y-3=m_2(x-4)

otteniamo in conclusione le equazioni delle rette tangenti alla circonferenza in esame e passanti per il punto {P}:

\small t_1:y-3=\left[ \dfrac{1}{34} \cdot \left( 55 + \sqrt{2226}\right) \right](x-4); \qquad t_2:y-3=\left[ \dfrac{1}{34} \cdot \left( 55 - \sqrt{2226}\right) \right](x-4); 

Vista la presenza dei termini irrazionali conviene in questo caso lasciare le equazioni delle rette tangenti in questa forma.

A seguire presentiamo l’applicazione per questo stesso esempio del metodo più generale, che richiede di impostare un sistema risolvente, in modo simile a quanto visto per la determinazione dei punti di intersezione circonferenza-retta.

Esempio (equazioni delle rette tangenti passanti per un punto esterno, con l’utilizzo del sistema risolvente)

Proviamo a risolvere il problema dell’esempio precedente impostando un sistema risolvente del tipo il seguente:

\begin{cases}\gamma : x^2+y^2+ax+by+c=0 \\ \\ t_{1,2}: y-y_P=m(x-x_P) \end{cases}

La prima equazione è l’equazione canonica della circonferenza in esame, mentre la seconda equazione rappresenta una delle due rette tangenti alla circonferenza e tali da passare per il punto {P=(x_P, y_P)}.

Osserviamo che con il simbolo {t_{1,2}} vogliamo intendere che l’equazione {y-y_P=m(x-x_P)} rappresenta entrambe le rette tangenti alla circonferenza e tali da passare per un dato punto {P} esterno alla circonferenza stessa.

A questo punto, si tratterà di esplicitare ad esempio la {y} dalla seconda equazione, e quindi sostituire l’espressione ottenuta nella prima equazione. In tal modo, ciò che si ottiene è un’equazione di secondo grado nella sola incognita {x} e con coefficienti in funzione del coefficiente angolare {m}.

Ora, poiché ricerchiamo le eventuali rette tangenti alla circonferenza, dobbiamo richiedere che la circonferenza e ciascuna retta tangente abbiano un unico punto di intersezione. Ma ciò ha come conseguenza che l’equazione di secondo grado risolvente deve avere due soluzioni reali e coincidenti. Quindi, dovremo imporre che il determinante {\Delta} relativo all’equazione sia uguale a zero. E poiché i coefficienti dell’equazione sono funzioni di {m}, la condizione {\Delta = 0} sarà un’equazione nell’incognita {m}. Basterà quindi risolvere l’equazione di secondo grado in {m} in modo da determinare i coefficienti angolari corrispondenti alle rette {t_1} e {t_2} tangenti alla circonferenza.

Passiamo subito al caso in esame. Il sistema risolvente è il seguente:

\begin{cases} \gamma: x^2+y^2+3x+4y-7=0 \\ \\ t_{1,2}: y-3=m(x-4)\end{cases}

Esplicitiamo la {y} dalla seconda equazione:

\begin{cases} \gamma: x^2+y^2+3x+4y-7=0 \\ \\ t_{1,2}: y=\boxed{m(x-4)+3}\end{cases}

Sostituiamo l’espressione per {y} appena ottenuta nella prima equazione:

\begin{cases} \gamma: x^2+\left[{ m(x-4)+3}\right]^2+3x+4[m(x-4)+3]-7=0 \\ \\ t_{1,2}: y={m(x-4)+3}\end{cases}

Ora concentriamoci sulla prima equazione e sviluppiamo i calcoli in essa presenti:

\small \begin{align*} & x^2+m^2(x-4)^2+9+6m(x-4)+3x+4(mx-4m+3)-7 = 0;  \\ \\ & x^2+m^2(x^2-8x+16)+9+6mx-24m+3x+4mx-16m+12-7=0;\\ \\ & x^2+m^2x^2-8m^2x+16m^2+9+6mx-24m+3x+4mx-16m+12-7=0;\\ \\ & (1+m^2)x^2+(-8m^2+6m+3+4m)x+16m^2+(-24-16)m+9+12-7=0;\\ \\ & (1+m^2)x^2+(-8m^2+10m+3)x+16m^2-40m+14=0\end{align*}

L’ultima equazione scritta è un’equazione di secondo grado nell’incognita {x} della forma {ax^2+bx+c=0}, con {a=1+m^2}, {b=-8m^2+10m+3} e {c=16m^2-40m+14}. Come già anticipato non ci interessa risolvere l’equazione rispetto ad {x}, ma piuttosto ricavare i valori di {m} imponendo la condizione:

\Delta =0

ovvero:

b^2-4ac=0

che nel nostro caso diviene:

\left( -8m^2+10m+3\right)^2-4 \cdot (1+m^2) \cdot (16m^2-40m+14)=0

Sviluppando i calcoli (ricordiamo la regola del quadrato di un trinomio) abbiamo:

\small \begin{align*} & 64m^4+100m^2+9-160m^3-48m^2+60m-4(16m^2-40m+14+16m^4-40m^3+14m^2)=0; \\ \\ & \cancel{64m^4}+100m^2+9-\cancel{160m^3}-48m^2+60m-{64m^2}+160m-56-\cancel{64m^4}+\cancel{160m^3}-56m^2=0;\\ \\ &(100-48-64-56)m^2+(60+160)m+9-56=0;\\ \\ & -68m^2+220m-47=0;\\ \\ & 68m^2-220m+47=0 \end{align*}

Ora non resta che risolvere l’equazione di secondo grado appena scritta rispetto ad {m}, ottenendo:

m_1=\dfrac{1}{34}\left(55+\sqrt{2226} \right); \qquad m_2=\dfrac{1}{34}\left( 55-\sqrt{2226}\right)

Sostituendo i valori di {m} nella seconda equazione del sistema di partenza abbiamo rispettivamente le due equazioni:

\begin{align*} &  t_1: y=\left[\dfrac{1}{34}\left(55+\sqrt{2226} \right)\right](x-4)+3; \\ \\ &t_2:y=\left[\dfrac{1}{34}\left(55-\sqrt{2226} \right)\right](x-4)+3 \end{align*}

Queste sono le equazioni (che accettiamo di lasciare in questa forma) delle rette tangenti alla circonferenza {\gamma} e tali da passare per il punto {P}. Esse corrispondono a quelle già determinate nell’esempio precedente utilizzando la formula della distanza punto-retta.

Circonferenza passante per tre punti non allineati

Se tre punti del piano sono tra loro non allineati, per essi passa un’unica circonferenza. Ciò discende da un noto teorema della geometria euclidea.

Di conseguenza, dati tre punti del piano non allineati tra loro, è possibile determinare l’equazione della circonferenza che passa per essi. Allo scopo, l’idea è quella di partire dall’equazione della circonferenza in forma canonica:

\gamma: x^2+y^2+ax+by+c=0

e mettere a sistema tre equazioni, ciascuna delle quali si ottiene sostituendo alle variabili {x} e {y} le coordinate di ciascuno dei tre punti dati. Infatti, se una circonferenza passa per tre punti, le condizioni di appartenenza di ciascun punto ad essa dovranno essere tutte verificate contemporaneamente.

Esempio 11

Verificare che i punti {A=(3, -2)}, {B=(4,1)} e {D=(7,5)} non sono allineati tra loro e quindi scrivere l’equazione in forma canonica della circonferenza passante per essi.

Per verificare che i tre punti non sono allineati tra loro, basta scrivere l’equazione della retta passante ad esempio per i due punti {A} e {B}, e quindi verificare che il rimanente punto {D} non appartiene a tale retta.

Ricordando la formula della retta passante per due punti, si ha:

\dfrac{x-x_A}{x_B-x_A}=\dfrac{y-y_A}{y_B-y_A}

ovvero sostituendo i valori delle coordinate dei punti {A} e {B}:

\begin{align*} &\dfrac{x-3}{4-3}=\dfrac{y+2}{1+2}; \\ \\ &x-3=\dfrac{y+2}{3}; \\ \\ & x-3-\dfrac{y+2}{3}=0;\\ \\ & 3x-9-y-2=0;\\ \\ & r_{AB}:y=3x-11\end{align*}

Ora, vediamo se il punto {D} appartiene alla retta passante per i punti {A} e {B}. Per fare questo, basta vedere se i valori delle coordinate del punto {D} soddisfano l’equazione della retta {r_{AB}}:

y=3x-11 \quad \text{con} \: x=7, \: y= 5 \quad \Rightarrow \quad 5=3 \cdot7-11 \quad \Rightarrow 5=10

Effettivamente otteniamo un’uguaglianza numerica falsa. Di conseguenza il punto {D} non appartiene alla retta passante per i punti {A} e {B} e quindi i tre punti non sono allineati.

Siamo allora certi che ha senso determinare l’equazione dell’unica circonferenza del piano passante per i tre punti in esame.

Sostituiamo nell’equazione canonica generica di una circonferenza di volta in volta le coordinate dei tre punti dati. Mettiamo a sistema le tre equazioni che così si ottengono. Abbiamo:

\begin{cases}  x^2+y^2+ax+by+c=0 \quad \text{con}\quad x=3, \: y=-2 \\ \\  x^2+y^2+ax+by+c=0 \quad \text{con}\quad  x=4, \: y= 1 \\ \\ x^2+y^2+ax+by+c=0 \quad \text{con}\quad x=7, \: y=5\\ \\  \end{cases}

e quindi:

\begin{cases} 9+4+3a-2b+c=0 \\ \\ 16+1+4a+b+c=0 \\ \\ 49+25+7a+5b+c=0\end{cases} \quad \Rightarrow \quad \begin{cases} 3a-2b+c+13 = 0 \\ \\ 4a+b+c+17=0 \\ \\ 7a+5b+c+74=0\end{cases}

da cui segue il sistema di tre equazioni in tre incognite in forma normale:

\begin{cases} 3a-2b+c=-13 \\ \\ 4a+b+c=-17 \\ \\ 7a+5b+c=-74\end{cases}

che risolto dà:

a=-31, \; b=9, \: c=98

Così in conclusione la circonferenza passante per i tre punti dati ha equazione in forma canonica:

x^2+y^2-31x+9y+98=0

Conclusioni

La lezione appena conclusa è sicuramente molto ampia ma offre una panoramica completa della circonferenza, letta dal punto di vista della geometria analitica. Nelle successive lezioni riprenderemo comunque i vari argomenti, in modo da consentirvi un utile approfondimento, con in più l’opportunità di allenarvi con schede di esercizi svolti organizzati per argomento.

Raccomandiamo fortemente di leggere le lezioni successive, poiché consentono di fissare meglio i concetti ed inoltre introducono argomenti non trattati in questa lezione, quali ad esempio tutte le condizioni necessarie e sufficienti per scrivere l’equazione di una circonferenza ed i fasci di circonferenze.

Un saluto a tutti voi e buon proseguimento con SìMatematica! 🙂