Retta passante per due punti

 - 

Coordinate cartesiane e retta nel piano

L’equazione di una retta del piano passante per due punti non allineati né orizzontalmente né verticalmente si scrive come (y – y₁)/(y₂ – y₁)=(x – x₁)/(x₂ – x₁), ove x₁, y₁ e x₂, y₂ sono le coordinate dei due punti stessi. L’obiettivo della lezione sarà proprio quello di mostrare come si arriva a questa equazione e come si risolve in generale il problema dello scrivere l’equazione di una retta del piano date le coordinate cartesiane di due punti ad essa appartenenti.

Ci occupiamo quindi di vedere come scrivere l’equazione di una retta del piano cartesiano passante per due punti, utilizzando diversi approcci.

Osserviamo fin da subito che il problema è ben posto. Infatti, una retta è univocamente determinata una volta noti due punti appartenenti ad essa. In altre parole, la retta del piano che passa per due punti dati è unica.

In una precedente lezione abbiamo visto come calcolare il coefficiente angolare di una retta a partire dalle coordinate di due punti della retta stessa. Inoltre, abbiamo anche visto come scrivere l’equazione di una retta avente una determinata pendenza e passante per un certo punto. Così, noti il coefficiente angolare e le coordinate di un punto appartenente ad una retta, è possibile scrivere l’equazione della retta stessa.

Ci occuperemo prima di tutto del caso di due punti distinti non allineati né verticalmente, né orizzontalmente. In altre parole, considereremo in prima istanza due punti {P_1=(x_1, y_1)} e {P_2=(x_2, y_2)} tali che:

x_1 \neq x_2 \quad \text{e contemporaneamente} \quad y_1 \ne y_2

Mostreremo poi come comportarci nel caso in cui, invece, i due punti siano allineati verticalmente oppure orizzontalmente.

Per meglio comprendere la lezione, ricordiamo che due punti allineati verticalmente condividono la stessa ascissa. E la retta passante per i due punti sarà una retta verticale. In altre parole, la retta forma con la direzione positiva dell’asse delle {x} un angolo uguale a 90 gradi.

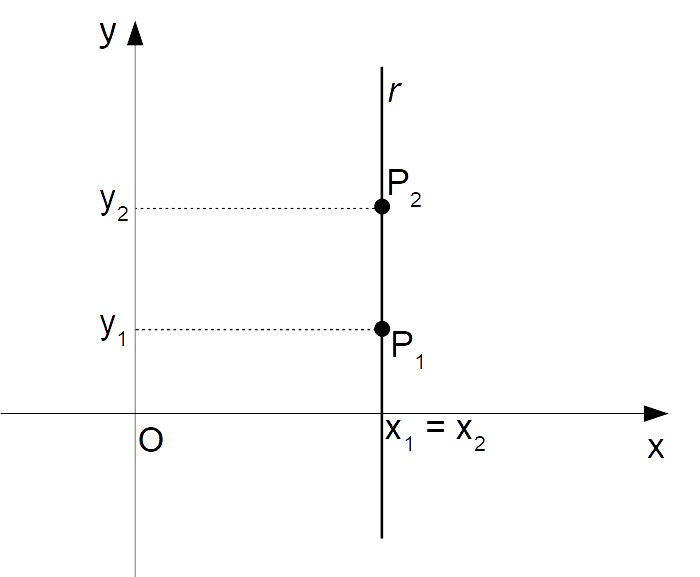
Viceversa, due punti allineati orizzontalmente condividono la stessa ordinata. E la retta passante per i due punti sarà in questo caso orizzontale, quindi tale da formare con la direzione positiva dell’asse delle {x} un angolo uguale a zero gradi.

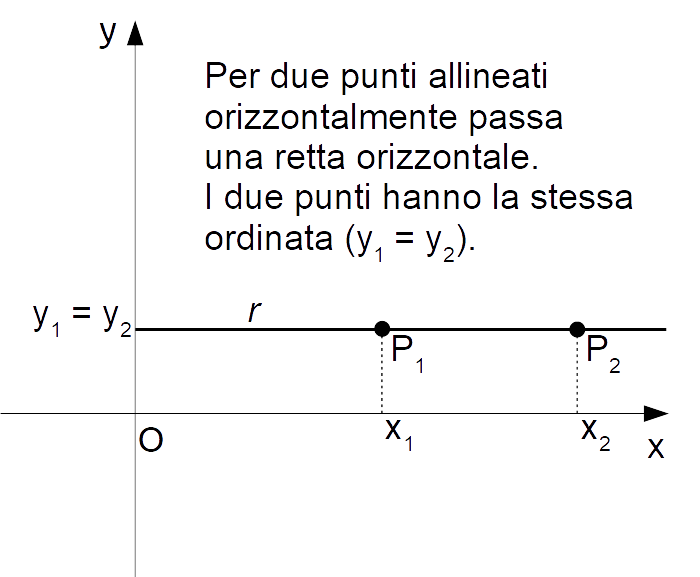
Scrivere l’equazione di una retta passante per due punti noti non allineati né verticalmente né orizzontalmente

Siano dati due punti appartenenti ad una certa retta {r} del piano cartesiano:

P_1 = (x_1, y_1), \qquad P_2=(x_2, y_2)

Sia {x_1 \neq x_2} e contemporaneamente {y_2 \neq y_2}. In altre parole, i due punti non siano allineati né verticalmente, né orizzontalmente.

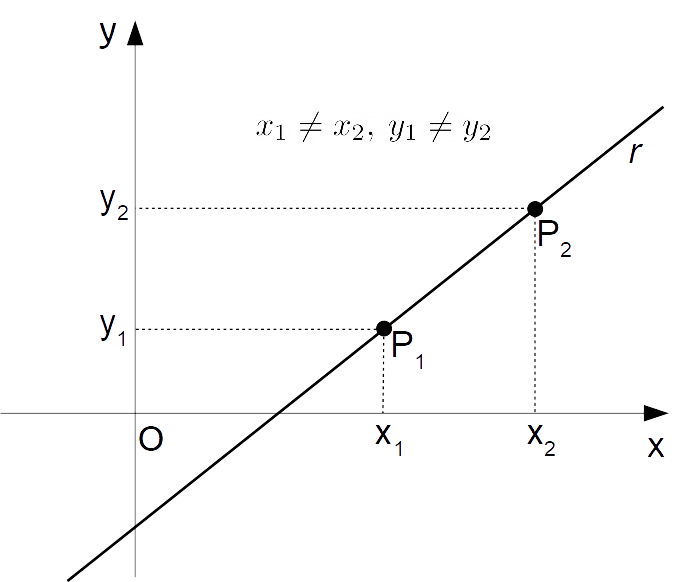
In parole povere, escludiamo per il momento rette orizzontali (di equazione {y=k}) o verticali (di equazione {x=k}), ove {k} è una costante reale.

Sotto tale ipotesi, possiamo calcolare il coefficiente angolare della retta {r} utilizzando le coordinate cartesiane dei punti {P_1} e {P_2}:

m=\dfrac{y_2-y_1}{x_2-x_1}

Nota: in realtà possiamo comunque calcolare il coefficiente angolare anche se i punti sono allineati orizzontalmente, ovvero si abbia {y_2=y_1}. In tale circostanza otteniamo infatti {m=0} e ricadiamo nel caso di una retta orizzontale.
Non è invece possibile calcolare il coefficiente angolare nel caso in cui i due punti siano allineati verticalmente. Sotto tale ipotesi avremmo infatti {x_1=x_2}, circostanza nella quale il denominatore {x_2-x_1} presente nell’espressione del coefficiente angolare si annulla.
Ci occuperemo comunque di questi casi in una successiva parte della lezione.

Ora, l’equazione di una retta di pendenza nota e passante per un punto {P_1 = (x_1, y_1)} di coordinate cartesiane note è:

y-y_1= m (x-x_1)

Dato che conosciamo i valori del coefficiente angolare {m} e delle coordinate {x_1} e {y_1}, dalla precedente è possibile ottenere mediante semplici calcoli l’equazione della retta {r} nella forma esplicita:

y=mx+q

Vediamo subito un esempio pratico.

Esempio (equazione di una retta passante per due punti)

Scrivere l’equazione della retta del piano cartesiano passante per i due punti {P_1 = (1,0)} e {P_2=(3,2)}.

Osserviamo anzitutto che i due punti non sono allineati né orizzontalmente, né verticalmente. Infatti valgono entrambe le relazioni:

y_1 \neq y_2, \qquad x_1 \neq x_2

In particolare, essendo {x_1 \neq x_2}, è possibile calcolare il coefficiente angolare della retta passante per i due punti a partire dalla coordinate cartesiane dei punti stessi. Abbiamo:

m = \dfrac{y_2-y_1}{x_2-x_1}=\dfrac{2-0}{3-1}=\dfrac{2}{2}=1

A questo punto sostituiamo il valore del coefficiente angolare e le coordinate ad esempio del punto {P_1} nell’equazione di una retta del piano cartesiano avente dato coefficiente angolare e passante per un punto noto:

y-y_1 = m (x-x_1)

otteniamo:

y-0=1 \cdot (x - 1)

da cui segue:

y=x-1

che è l’equazione in forma esplicita della retta cercata. In forma implicita l’equazione diviene infine:

y-x+1=0 \quad \Rightarrow \quad -x+y+1=0

Forma generale dell’equazione di una retta del piano cartesiano passante per due punti non allineati né orizzontalmente né verticalmente

E’ possibile mettere insieme l’espressione per il coefficiente angolare precedentemente scritta e l’equazione di una retta di pendenza nota e passante per un punto di coordinate assegnate. In tal modo, possiamo ottenere la forma generale dell’equazione di una retta passante per due punti.

Partiamo quindi dall’espressione del coefficiente angolare in funzione delle coordinate di due punti appartenenti alla retta considerata:

m=\dfrac{y_2-y_1}{x_2-x_1}

Ricordiamo che abbiamo ricavato questa espressione a partire dalla condizione di appartenenza di un punto ad una retta e utilizzando il primo principio di equivalenza delle equazioni (vedi lezione sul coefficiente angolare).

Consideriamo inoltre l’equazione di una retta di pendenza nota passante per un punto {P_1=(x_1, y_1)} assegnato:

y-y_1 = m (x-x_1)

Sostituendo ad {m} la corrispondente espressione in funzione delle coordinate cartesiane dei punti {P_1 = (x_1, y_1)} e {P_2=(x_2, y_2)} appartenenti alla retta abbiamo:

y-y_1= \dfrac{y_2-y_1}{x_2-x_1}(x-x_1)

Ora, possiamo certamente supporre {y_2 - y_1 \neq 0}, ovvero {y_2 \neq y_1}. Infatti, stiamo considerando rette i cui punti non sono allineati né orizzontalmente, né verticalmente. Così, dividendo entrambi i membri della precedente equazione per {y_2-y_1} otteniamo:

\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}

equazione valida per {y_2 \neq y_1} e {x_2 \neq x_1}. Diversamente infatti le frazioni algebriche al primo e secondo membro non avrebbero significato.

Riassumiamo ora quanto sin qui ricavato.

L’equazione di una retta passante per due punti {P_1 = (x_1, y_1)} e {P_2=(x_2, y_2)} non allineati né verticalmente né orizzontalmente è data da:{\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}}

Osserviamo che le condizioni {y_2 \neq y_1} e {x_2 \neq x_1} effettivamente equivalgono a richiedere che i due punti {P_1} e {P_2} non siano allineati né orizzontalmente, né verticalmente. Così, l’equazione in esame può rappresentare unicamente rette non parallele agli assi coordinati, ovvero rette né orizzontali, né verticali.

L’equazione di una retta passante per due punti nella forma appena scritta consente di scrivere direttamente l’equazione di una retta una volta note le coordinate di due suoi punti, senza dover preventivamente calcolare il coefficiente angolare. Ovviamente, per utilizzare tale equazione dovremo prima verificare che i due punti dati non siano allineati né orizzontalmente, né verticalmente.

Esempio (retta per due punti senza dover calcolare il coefficiente angolare)

Scrivere l’equazione della retta del piano cartesiano passante per i due punti {P_1=(-3, 4)} e {P_2 = (2, -7)}.

Osserviamo che i due punti non sono allineati né verticalmente, né orizzontalmente. Infatti, l’ascissa del punto {P_1} è diversa dall’ascissa del punto {P_2}. Di conseguenza, non abbiamo l’allineamento verticale tra i due punti. Inoltre, l’ordinata del punto {P_1} è diversa dall’ordinata del punto {P_2}. Pertanto, non abbiamo nemmeno l’allineamento orizzontale tra i due punti stessi.

Partiamo direttamente dall’equazione:

\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}

e sostituiamo in essa le coordinate dei punti a noi note (come sempre, attenzione ai segni):

\dfrac{y-4}{-7-4}=\dfrac{x-(-3)}{2-(-3)}

Otteniamo:

\dfrac{y-4}{-11}=\dfrac{x+3}{5}

Proviamo a riscrivere l’equazione così ottenuta ad esempio in forma implicita, ovvero nella forma {ax+by+c=0}. Cominciamo mettendo tutti i termini al primo membro:

\dfrac{y-4}{-11}-\dfrac{x+3}{5}=0

Per fare ciò abbiamo semplicemente trasportato al primo membro la frazione algebrica che si trovava al secondo membro, cambiando il segno davanti al simbolo di fratto.

A questo punto, mettiamo i termini a denominatore comune:

\dfrac{5y-20+11x+33}{-55}=0

Possiamo direttamente eliminare il denominatore senza alcuna discussione. Questi è infatti un numero. Sommando inoltre i termini simili tra loro otteniamo in conclusione l’equazione:

5y+11x+13=0

ovvero, riordinando i termini:

11x+5y+13=0

Ora l’equazione della retta è data nella forma implicita, ovvero nella forma {ax+by+c=0}, con {a=11, b=5} e {c=13}.

Ci rimane ora da esaminare i casi di due punti allineati orizzontalmente oppure verticalmente.

Equazione di una retta a partire da due punti allineati orizzontalmente

Osserviamo anzitutto che due punti sono allineati orizzontalmente se condividono la stessa ordinata. In altre parole, dati due punti del piano cartesiano:

P_1=(x_1, y_1), \qquad P_2=(x_2, y_2)

questi sono allineati orizzontalmente se e solo se:

y_1=y_2

In tal caso, l’equazione della retta alla quale appartengono entrambi i punti dati si scrive come:

y=y_1

oppure, il che è lo stesso:

y=y_2

Nota. E’ anche possibile pervenire a questo stesso risultato calcolando il coefficiente angolare e quindi utilizzando l’equazione di una retta noti la sua pendenza e le coordinate di un suo punto. Infatti, per due punti allineati orizzontalmente è possibile calcolare il coefficiente angolare della retta passante per essi (che come vedremo fra un istante, sarà nullo).
Così, per il coefficiente angolare abbiamo: {m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{0}{x_2-x_1}=0}E quindi: {y-y_1 = 0 \cdot (x-x_1) \quad \Rightarrow \quad y-y_1 = 0 \quad \Rightarrow \quad y=y_1} Ritroviamo così l’equazione di una retta orizzontale.

Esempio (due punti allineati orizzontalmente)

Scrivere l’equazione della retta passante per i due punti {P_1=(2,5)} e {P_2=(4,5)}.

Osserviamo che i due punti hanno la stessa ordinata e quindi sono allineati orizzontalmente. Di conseguenza, l’equazione della retta è della forma {y=k}, con {k \in \R}, ovvero in questo caso:

y=5

ove al secondo membro abbiamo l’ordinata comune ai punti della retta. Ricordiamo che una tale retta è orizzontale, ovvero parallela all’asse {x}.

Equazione di una retta a partire da due punti allineati verticalmente

Per due punti {P_1=(x_1, y_1)} e {P_2=(x_2, y_2)} tali da essere allineati verticalmente deve valere necessariamente:

x_1 = x_2

L’equazione della retta passante per i due punti è data da:

x = x_1

oppure, il che è lo stesso:

x=x_2

Non è possibile in questo caso calcolare il coefficiente angolare, in quanto i due punti hanno la stessa ascissa e di conseguenza nell’espressione del coefficiente angolare:

m=\dfrac{y_2-y_1}{x_2-x_1}

il denominatore si annulla.

Esempio (due punti allineati verticalmente)

Scrivere l’equazione della retta passante per i punti {P_1=(2,5)} e {P_2=(2,-3)}.

Poiché abbiamo {x_1=x_2} i due punti sono allineati verticalmente. L’equazione della retta passante per i due punti è:

x=2

ove al secondo membro abbiamo l’ascissa in comune ai due punti per i quali passa la retta.

Ricordiamo che una tale retta è verticale, ovvero parallela all’asse {y}.

Espressione dell’ordinata all’origine in funzione delle coordinate cartesiane di due punti di una retta del piano

Dall’equazione in forma esplicita di una retta del piano cartesiano è possibile ricavare un’espressione per l’ordinata all’origine {q}:

y=mx+q \quad \Rightarrow \quad q=y-mx

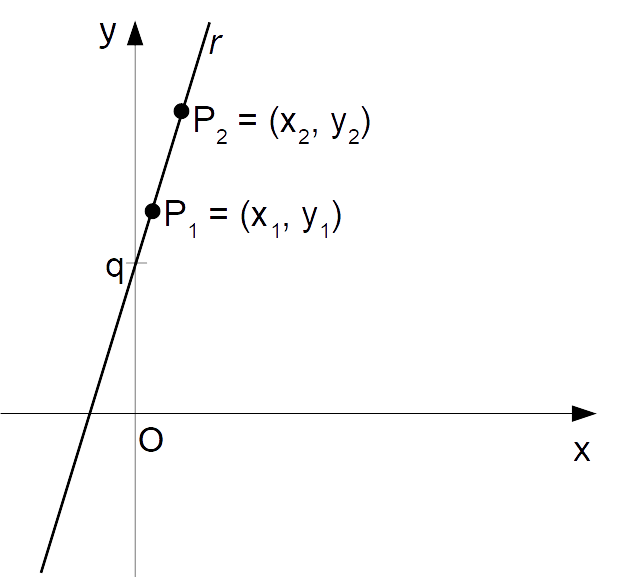
Ora, se un punto {P_1=(x_1,y_1)} appartiene alle retta, per la condizione di appartenenza del punto alla retta dovrà anche essere:

q=y_1-mx_1

E poiché come sappiamo, se anche il punto {P_2=(x_2, y_2)} appartiene alla retta in esame:

m=\dfrac{y_2-y_1}{x_2-x_1}

Sostituendo {m} nella precedente espressione ottenuta per {q} abbiamo:

q=y_1-\dfrac{y_2-y_1}{x_2-x_1}x_1

Mettendo i termini al secondo membro a denominatore comune:

q=\dfrac{y_1(x_2-x_1)-x_1(y_2-y_1)}{x_2-x_1}

Svolgendo i calcoli al numeratore:

q=\dfrac{x_2y_1-\cancel{x_1y_1}-x_1y_2+\cancel{x_1y_1}}{x_2-x_1}

ovvero in conclusione:

q=\dfrac{x_2y_1-x_1y_2}{x_2-x_1}

o il che è lo stesso (invertendo i segni di tutti i termini sia al numeratore, sia al denominatore):

q=\dfrac{x_1y_2-x_2y_1}{x_1-x_2}

la quale rappresenta un’espressione per l’ordinata all’origine {q} in funzione delle coordinate di due punti appartenenti alla retta in esame, nel caso in cui sia {x_1 \neq x_2}. L’espressione appena ottenuta è dunque valida per una qualunque retta del piano cartesiano purché non verticale.

E’ dunque possibile ricavare l’ordinata all’origine {q} di una retta non verticale a partire dalle coordinate cartesiane di due punti ad essa appartenenti, in modo del tutto simile all’utilizzo della formula per ricavare il coefficiente angolare {m} sempre a partire da dette coordinate cartesiane. Ciò suggerisce un ulteriore metodo per scrivere l’equazione di una retta passante per due dati punti, come mostra l’esempio immediatamente a seguire.

Esempio (retta per due punti calcolando m e q)

Scrivere l’equazione della retta passante per i punti {P_1=(-1,-3)} e {P_2=(5,-4)}.

Osserviamo che i due punti non sono allineati né orizzontalmente, né verticalmente. Di conseguenza, è possibile ricavare sia il coefficiente angolare, sia l’ordinata all’origine della retta passante per i due punti stessi. Tenendo conto delle coordinate dei punti abbiamo:

\begin{align*} & m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{-4-(-3)}{5-(-1)}=\dfrac{-1}{6}=-\dfrac{1}{6}; \\ \\ & q=\dfrac{x_1y_2-x_2y_1}{x_1-x_2}=\dfrac{-1 \cdot (-4) - 5 \cdot (-3)}{-1-5} =\dfrac{4+15}{-6}=-\dfrac{19}{6}\end{align*}

Ora non resta che sostituire i valori ottenuti per {m} e {q} nell’equazione di una retta del piano in forma esplicita:

y=mx+q

otteniamo in conclusione:

\boxed{y=-\dfrac{1}{6}x-\dfrac{19}{6}}

Utilizzando gli altri metodi sin qui visti ritroviamo lo stesso risultato. Infatti, partendo dall’espressione di una retta passante per due punti:

\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}

sostituendo le coordinate dei punti otteniamo:

\dfrac{y-(-3)}{-4-(-3)}=\dfrac{x-(-1)}{5-(-1)}

ovvero:

\begin{align*} &\dfrac{y+3}{-1}=\dfrac{x+1}{6} \quad \Rightarrow \quad -3-y=\dfrac{x+1}{6} \quad \Rightarrow \quad -y=\dfrac{x+1}{6}+3 \\ \\ & \Rightarrow \quad -y=\dfrac{x+1+18}{6} \quad \Rightarrow \quad -y=\dfrac{x+19}{6} \quad \Rightarrow \quad \boxed{y=-\dfrac{1}{6}x-\dfrac{19}{6}}\end{align*}

Infine, anche calcolando il coefficiente angolare e quindi sostituendo il valore ottenuto nell’equazione di una retta con pendenza e coordinate di un punto noti comunque ritroviamo:

\begin{align*} & m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{-4-(-3)}{5-(-1)}=\dfrac{-1}{6}=-\dfrac{1}{6};  \\ \\ & y-y_1 = m(x-x_1) \quad \Rightarrow \quad y-(-3)=-\dfrac{1}{6} \cdot [x-(-1)] \\ \\ & \Rightarrow \quad y+3=-\dfrac{1}{6}(x+1) \quad \Rightarrow \quad y+3=-\dfrac{1}{6}x-\dfrac{1}{6} \\ \\ & \Rightarrow \quad y=-\dfrac{1}{6}x-\dfrac{1}{6}-3 \quad \Rightarrow \quad \boxed{y=-\dfrac{1}{6}x-\dfrac{19}{6}}\end{align*}

Conclusioni

Per quanto riguarda questa lezione sulla retta passante per due punti è tutto. Abbiamo così visto come scrivere l’equazione di una retta del piano cartesiano passante per due punti di coordinate note utilizzando tre differenti metodi (nell’ipotesi di punti non allineati né orizzontalmente, né verticalmente):

• calcolo del coefficiente angolare con la formula {m=\dfrac{y_2-y_1}{x_2-x_1}} e utilizzo dell’equazione di una retta del piano nella forma {y-y_1 = m (x - x_1)};
• utilizzo diretto dell’equazione della retta del piano cartesiano passante per due punti non allineati né orizzontalmente, né verticalmente: {\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}};
• calcolo del coefficiente angolare e dell’ordinata all’origine, sempre a partire dalle coordinate dei due punti dati, rispettivamente con le formule {m=\dfrac{y_2-y_1}{x_2-x_1}} e {q=\dfrac{x_1y_2-x_2y_1}{x_1-x_2}}, per poi utilizzare l’equazione esplicita di una retta del piano, ovvero {y=mx+q}.

Infine, abbiamo visto come operare nel caso di punti allineati orizzontalmente (utilizzo dell’equazione {y=k}) e verticalmente (utilizzo dell’equazione {x=k}), ove {k} è rispettivamente l’ordinata o l’ascissa di uno dei due punti dati.

Quale metodo utilizzare? Chi scrive trova comodo il primo metodo, ma la scelta è comunque personale e in ogni caso dovrà tenere conto delle indicazioni del proprio insegnante.

Ora è davvero tutto. Nella prossima lezione ci occuperemo delle condizioni di parallelismo delle rette del piano. E nelle lezioni ancora a seguire vedremo le condizioni di perpendicolarità delle rette del piano, come determinare l’eventuale punto di intersezione tra due rette del piano e infine introdurremo la definizione di fascio di rette (proprio e improprio). Buon proseguimento con SìMatematica! 🙂