Rette parallele

 - 

Coordinate cartesiane e retta nel piano

Due rette del piano con equazioni espresse in forma esplicita sono parallele tra loro se hanno lo stesso coefficiente angolare. Più in generale, inoltre, se le due rette hanno equazioni date in forma implicita, queste sono parallele tra loro se i coefficienti delle incognite sono tra loro proporzionali.

In questa lezione ci occuperemo della definizione di rette parallele e vedremo le relative condizioni di parallelismo, a seconda che le equazioni delle rette siano in forma esplicita o in forma implicita. Tale distinzione si giustifica osservando che nel caso di rette con equazioni date in forma esplicita, l’individuazione dei coefficienti angolari è immediata. Diversamente, per le equazioni in forma implicita i coefficienti angolari a rigore dovrebbero essere calcolati (escluso il caso di rette verticali) a partire dai coefficienti dei termini in {x} e {y} che compaiono nelle equazioni. Tuttavia, nel corso della lezione mostreremo come ricavare una condizione di parallelismo tra rette che fa uso direttamente dei coefficienti che figurano nelle equazioni delle rette in forma implicita.

Il punto di partenza sul quale si baseranno le varie conclusioni che trarremo lungo il percorso sarà dato dal dimostrare che le rette {y=mx+q} e {y=mx} sono parallele tra loro (fissato lo stesso {m}). Da ciò, riuscirà evidente la condizione di uguaglianza dei coefficienti angolari per poter parlare di parallelismo tra rette. E da tale ragionamento discenderà infine la condizione di parallelismo per rette con equazioni espresse anche nella forma implicita.

Rette parallele: introduzione

Fissato un certo valore del coefficiente angolare {m}, consideriamo le due rette:

y=mx+q, \qquad y=mx

Fissato anche un certo valore dell’ordinata all’origine {q}, tracciamo entrambe le rette. Consideriamo inoltre due punti appartenenti alla retta di equazione {y=mx}, ad esempio i due punti {O} e {P} in figura.

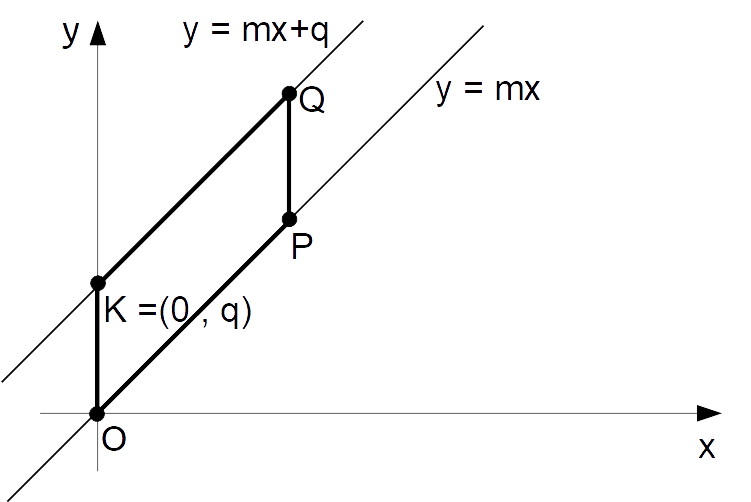
Ora, i punti {K} e {Q} appartenenti alla retta {y=mx+q} si ottengono a partire dai punti {O} e {P} operando una traslazione verticale di distanza {q}. In altre parole, i punti {K} e {Q} si ottengono a partire dai punti {O} e {P} sommando all’ordinata di questi ultimi una stessa quantità {q}, lasciando invariata la loro ascissa.

Pertanto, il quadrilatero {OPQK} è un parallelogramma (lati a due a due paralleli), e di conseguenza le rette y=mx e y=mx+q sono tra loro parallele. Ed osserviamo che le due rette hanno lo stesso coefficiente angolare.

In generale, per due qualsiasi rette aventi lo stesso coefficiente angolare valgono ancora le considerazioni sin qui fatte. Di conseguenza, possiamo affermare quanto segue.

Se due rette hanno lo stesso coefficiente angolare, queste sono tra loro parallele.

Vale inoltre il viceversa.

Se due rette sono parallele, allora queste hanno lo stesso coefficiente angolare.

Quindi in conclusione due rette sono parallele tra loro se e solo se hanno lo stesso coefficiente angolare.

A seguire procederemo a formalizzare le condizioni di parallelismo tra rette nei differenti casi in cui le equazioni siano date rispettivamente in forma esplicita ed implicita.

Condizione di parallelismo tra rette con equazioni date in forma esplicita

Date due rette {r_1} ed {r_2}, aventi rispettivamente equazioni:{r_1: y=m_1x+q_1, \qquad r_2:y=m_2x+q_2}queste sono parallele se e solo se vale la condizione: {m_1=m_2}ovvero se le due rette hanno lo stesso coefficiente angolare.

Vediamo subito degli esempi su come riconoscere due rette parallele nel caso di equazioni date in forma esplicita.

Esempi (rette parallele con equazioni in forma esplicita)

Esempio 1

Stabilire se le rette {r_1: y=2x+5} e {r_2: y=2x+7} sono parallele o meno tra loro.

Ricordiamo come sempre che una retta in forma esplicita ha equazione:

y=mx+q

Così nel caso della retta {r_1} abbiamo {m = 2} e {q=5} mentre nel caso della retta {r_2} abbiamo {m=2} e {q=7}. Indichiamo il coefficiente angolare e l’ordinata all’origine delle rette {r_1} ed {r_2} rispettivamente con {m_1, q_1} e {m_2, q_2}.

Per tutto quanto sin qui detto, la prima retta ha coefficiente angolare:

m_1 = 2

mentre la seconda ha coefficiente angolare:

m_2 = 2

Dato che i due coefficienti angolari sono uguali, ovvero risulta verificata l’uguaglianza:

m_1 = m_2

possiamo concludere che le due rette sono parallele. Di ciò otteniamo conferma disegnando le rette sul piano cartesiano:

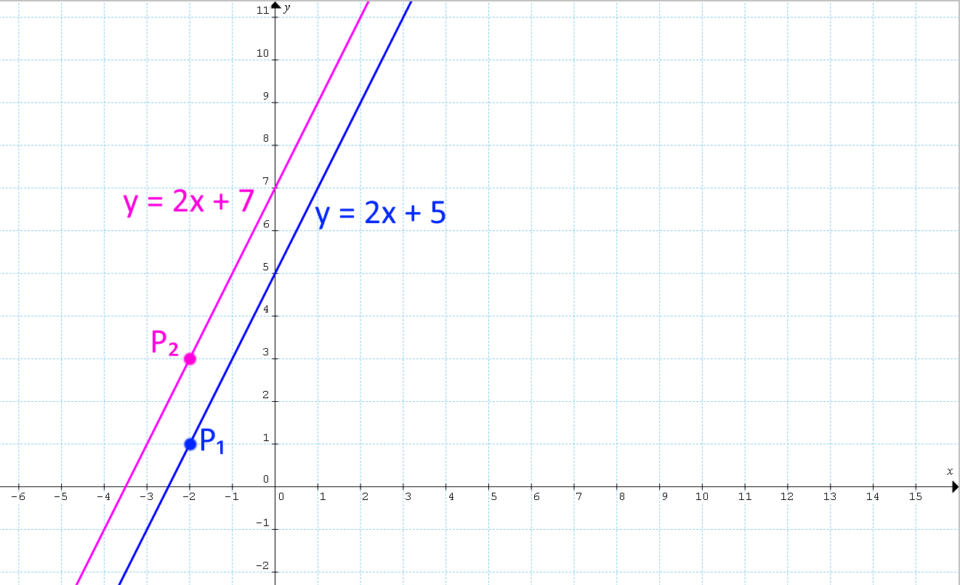
Le due rette sono parallele tra loro e distinte poiché le rispettive ordinate all’origine sono differenti ({q_1 \neq q_2)}.

Esempio 2

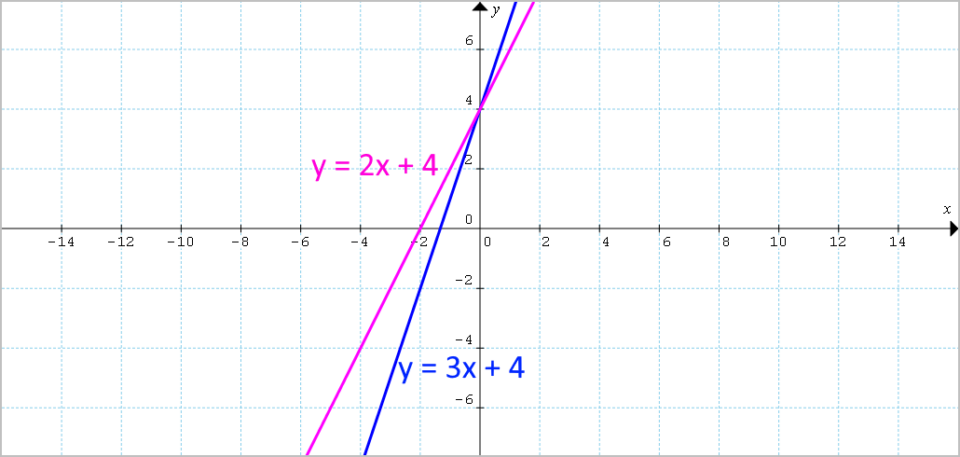
Stabilire se le rette {r_1: y = 3x+4} e {r_2 : y=2x+4 } sono parallele tra di loro.

E’ immediato concludere che le due rette non sono parallele tra loro in quanto hanno differente coefficiente angolare. La prima retta ha infatti coefficiente angolare {m_1=3} mentre la seconda retta ha coefficiente angolare {m_2=2}.

Condizione di parallelismo tra rette con equazioni date in forma implicita

Consideriamo una retta {r_1} di equazione:

a_1x+b_1y+c_1=0, \qquad a_1,b_1,c_1 \in \R

con {a_1, b_1} mai contemporaneamente nulli.

Come già sappiamo, escluso il caso di rette verticali è possibile riscrivere l’equazione in forma esplicita, in modo da ricavare un’espressione per il coefficiente angolare {m} (che in questo caso indicheremo con {m_1} in quanto relativo alla retta {r_1}):

y=-\dfrac{a_1}{b_1}x-\dfrac{c_1}{b_1} \quad \Rightarrow \quad m_1 = -\dfrac{a_1}{b_1}

Così, allo stesso modo, una retta {r_2} avente equazione {a_2x+b_2y+c_2=0} avrà coefficiente angolare:

m_2=-\dfrac{a_2}{b_2}

Ora, le due rette {r_1} ed {r_2} saranno parallele tra loro se e solo se i rispettivi coefficienti angolari sono uguali:

m_1 = m_2

ovvero, utilizzando i coefficienti delle incognite che compaiono nelle equazioni in forma implicita:

-\dfrac{a_1}{b_1}=-\dfrac{a_2}{b_2}

cioè:

\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}

Infine, moltiplicando entrambi i membri per { \dfrac{b_1}{a_2}}:

\dfrac{a_1}{\cancel{b_1}} \cdot \dfrac{\cancel{b_1}}{a_2}=\dfrac{\cancel{a_2}}{b_2} \cdot  \dfrac{b_1}{\cancel{a_2}}

da cui in conclusione:

\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}

che è la condizione di parallelismo per due rette non parallele agli assi coordinati e le cui equazioni sono date in forma implicita.

Due rette {r_1} ed {r_2} non parallele agli assi aventi equazioni: {r_1: a_1x+b_1y+c_1=0, \qquad r_2: a_2x+b_2y+c_2=0}sono tra loro parallele se e solo se i coefficienti delle incognite che compaiono nelle rispettive equazioni sono proporzionali tra loro, ovvero se e solo se:{\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}}

Il caso delle rette verticali ed orizzontali è qui escluso poiché in entrambi i casi potrebbe annullarsi almeno uno dei denominatori della relazione di parallelismo appena data.

D’altro canto, è comunque immediato riconoscere le equazioni di rette orizzontali o verticali e quindi regolarsi di conseguenza sulle condizioni di parallelismo. Ricordiamo infatti che le rette orizzontali e verticali sono rispettivamente della forma {y=k} (rette orizzontali) e {x=k} (rette verticali).

Esempi (rette parallele, caso di equazioni date in forma implicita)

Esempio 1

La retta {r_1:2x+5y+7=0} è parallela alla retta {r_2: 4x+10y-2=0}?

Indichiamo in forma generale la retta {r_1} con:

r_1 = a_1x+b_1y+c_1=0

e la retta {r_2} con:

r_2 = a_2x+b_2y+c_2=0

Così nel nostro caso abbiamo {a_1=2, b_1 = 5} e {a_2 = 4, b_2 = 10}. Controlliamo se tali coefficienti rispettano la condizione di parallelismo precedentemente enunciata:

\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2} \iff \dfrac{2}{4}=\dfrac{5}{10} \quad \Rightarrow \quad \dfrac{1}{2}=\dfrac{1}{2}

Avendo ottenuto un’uguaglianza numerica vera la condizione di parallelismo è rispettata. Di conseguenza, le rette {r_1} ed {r_2} sono tra loro parallele.

Esempio 2

Stabilire se sono parallele tra loro le rette di equazioni {r_1: 2x+3y+7=0} e {r_2:6x+5y-1=0}

Per la retta {r_1} abbiamo {a_1=2} e {b_1=3}, mentre per la retta {r_2} abbiamo {a_2 = 6} e {b_2 = 5}. Si ha:

\dfrac{a_1}{a_2}=\dfrac{2}{6}=\dfrac{1}{3}; \qquad \dfrac{b_1}{b_2}=\dfrac{3}{5} \qquad \Rightarrow \quad \dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}

Poiché non vale la condizione di parallelismo le due rette non sono parallele tra loro.

Esempio 3

Stabilire se sono parallele tra loro le rette di equazione {r_1: 2x+4y+8=0} e {r_2: x+2y+4 = 0}

In questo caso basta osservare che in forza al secondo principio di equivalenza è possibile dividere ciascun termine dell’equazione della retta {r_1} per {2}:

\dfrac{2}{2}x+\dfrac{4}{2}y+\dfrac{8}{2}=0 \quad \Rightarrow \quad x+2y+4=0

Abbiamo in questo modo ottenuto per la retta {r_1} un’equazione identica a quella della retta {r_2}. Di conseguenza le rette {r_1} ed {r_2} sono coincidenti e pertanto parallele tra loro.

Parallelismo tra rette come relazione di equivalenza.
Osserviamo che ogni retta è parallela a sé stessa. Ed è proprio per tale motivo che è possibile affermare che se due rette sono coincidenti (ovvero sono la stessa retta) allora queste sono parallele tra loro.
In particolare, la relazione di parallelismo tra rette è una relazione di equivalenza in quanto ogni retta è parallela a sé stessa (proprietà riflessiva), se la retta {r_1} è parallela alla retta {r_2} allora anche la retta {r_2} è parallela alla retta {r_1} (proprietà simmetrica), ed infine se la retta {r_1} è parallela alla retta {r_2}, e se la retta {r_2} è parallela alla retta {r_3}, allora anche la retta {r_1} è parallela alla retta {r_3} (proprietà transitiva).

Finora ci siamo occupati di esempi sul parallelismo tra rette nei quali abbiamo avuto a che fare con rette non parallele agli assi coordinati. Negli esempi a seguire mostreremo invece dei casi ove almeno una delle due rette in esame è parallela ad uno degli assi coordinati. Sottolineiamo che in circostanze di questo tipo la condizione di parallelismo data in precedenza non è utilizzabile, ma basta ragionare sulle equazioni di ciascuna retta.

Esempi (casi ove almeno una delle due rette è parallela ad uno degli assi coordinati)

Esempio 4

Stabilire se le rette di equazioni {r_1: y=5} e {r_2: x=-3} sono parallele tra loro.

Osserviamo che la retta {r_1} è parallela all’asse {x}. Questa è infatti data da punti aventi tutti la stessa ordinata. In modo del tutto simile, la retta {r_2} è parallela all’asse {y} in quanto costituita da punti aventi tutti la stessa ascissa. Di conseguenza, le due rette non sono parallele tra loro poiché ciascuna è parallela ad un differente asse coordinato.

Esempio 5

Stabilire se le rette {r_1: x=-5} e {r_2:x+y-8=0} sono parallele tra loro.

Osserviamo che la retta {r_1} è parallela all’asse {y}, mentre la retta {r_2} non è parallela agli assi coordinati. Di conseguenza, le due rette hanno necessariamente differente pendenza e non sono in conclusione parallele tra loro.

Precisiamo che il fatto che la retta {r_2} non è parallela agli assi coordinati discende immediatamente dalla forma della sua equazione. In generale, infatti, se nell’equazione di una retta in forma implicita abbiamo entrambi i coefficienti dei termini in {x} e {y} diversi da zero, l’equazione stessa non potrà ridursi né alla forma {x=k} né alla forma {y=k}, e quindi la retta risulterà necessariamente non parallela agli assi coordinati.

Condizione di parallelismo tra rette con equazioni date in forme differenti

A conclusione della lezione vogliamo occuparci del caso di rette non parallele agli assi coordinati con equazioni date in forme differenti. In particolare, consideriamo il caso di due rette delle quali una ha equazione data in forma esplicita mentre l’altra ha equazione data in forma implicita.

Esempio (verifica della condizione di parallelismo tra rette con equazioni date in differenti forme)

Stabilire se le rette di equazioni {r_1: y=2x-7} e {r_2:3x-4y+1=0} sono parallele tra loro.

Volendo utilizzare la condizione di parallelismo tra rette con equazioni date in forma implicita, l’idea è quella di lavorare sull’equazione della retta {r_1} in modo da ricondurla alla forma implicita. A tal punto ci ritroveremo con due equazioni entrambe in forma implicita e sarà possibile utilizzare la condizione di parallelismo:

\dfrac{a_1}{a_2}=\dfrac{b_1}{b_2}

Per l’equazione della retta {r_1} abbiamo:

y=2x-7 \quad \Rightarrow \quad 2x-y-7=0

L’equazione è ora in forma implicita, ed abbiamo {a_1=2} e {b_1=-1}. Per l’equazione della retta {r_2}, già data in forma implicita, abbiamo {a_2=3} e {b_2=-4}. Utilizzando la condizione di parallelismo precedentemente richiamata abbiamo:

\dfrac{a_1}{a_2}=\dfrac{2}{3}; \qquad \dfrac{b_1}{b_2}=\dfrac{-1}{-4}=\dfrac{1}{4} \qquad \Rightarrow \quad \dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}

Poiché la condizione di parallelismo non è verificata concludiamo che le due rette non sono parallele tra loro.

In alternativa, avremmo anche potuto ricondurre l’equazione della retta {r_2} alla forma esplicita, per poi confrontare tra loro i coefficienti angolari delle due rette. Così, per l’equazione della retta {r_2}, che in partenza è data in forma implicita, abbiamo:

\small 3x-4y+1=0 \quad \Rightarrow \quad -4y=-3x-1 \quad \Rightarrow \quad y=\dfrac{3}{4}x+\dfrac{1}{4}

Di conseguenza la retta {r_2} ha coefficiente angolare {m_2 = \dfrac{3}{4}}, mentre la retta {r_1} ha coefficiente angolare {m_1=2}. Nel caso della retta {r_1} il coefficiente angolare è immediatamente ricavabile poiché l’equazione è già data nella forma esplicita. Ricordiamo ancora una volta infatti che il coefficiente angolare di una retta è il coefficiente del termine in {x} relativo all’equazione della retta stessa data esclusivamente in forma esplicita (ovvero nella forma {y=mx+q}).

In conclusione, poiché {m_1 \neq m_2} ritroviamo anche utilizzando questo procedimento alternativo che le due rette non sono parallele tra loro.

Attenzione. Precisiamo che per una retta non parallela agli assi coordinati di equazione {ax+by+c=0}, il coefficiente angolare non è il coefficiente del termine in {x}. Infatti, l’equazione è data in forma implicita. In questo caso il coefficiente {m} è dato da {m=-\dfrac{a}{b}}.
Invece, per una retta con equazione data in forma esplicita, ovvero nella forma {y=mx+q}, effettivamente il coefficiente angolare è dato direttamente dal coefficiente del termine in {x}.

Conclusioni

Per questa lezione su come stabilire quando due rette sono parallele è tutto. Nella prossima lezione ci occuperemo invece di un altro interessante problema, ovvero capire quando due rette sono tra loro perpendicolari. Buon proseguimento con SìMatematica! 🙂