Rette perpendicolari

 - 

Coordinate cartesiane e retta nel piano

Due rette del piano sono perpendicolari tra loro se e solo se il prodotto dei rispettivi coefficienti angolari è uguale a -1. Nel corso della lezione ricaveremo proprio questa regola, a partire dal caso particolare di rette perpendicolari tra loro e passanti per l’origine degli assi.

Così dopo aver visto quando due rette sono parallele tra loro, ci preoccuperemo ora di caratterizzare la loro perpendicolarità. In altre parole, il nostro obiettivo sarà quello di determinare sotto quali condizioni due rette del piano cartesiano risultano tra loro perpendicolari.

Dal punto di vista geometrico, due rette del piano sono perpendicolari tra loro se formano quattro angoli tutti di ampiezza uguale a 90°. Tuttavia, ciò che desideriamo è ricavare una relazione di perpendicolarità fra rette del piano a partire dai rispettivi coefficienti angolari. Ed inoltre, vogliamo estendere tale relazione anche al caso di rette le cui equazioni sono date nella forma implicita. In tal modo, sarà possibile stabilire se due rette sono perpendicolari tra loro o meno a partire dai coefficienti che compaiono nelle incognite delle equazioni in forma implicita delle rette stesse.

Quando due rette del piano sono tra loro perpendicolari

Consideriamo due rette del piano {r_1} ed {r_2} tra loro perpendicolari e non passanti per l’origine, e consideriamo inoltre due rette {s_1} ed {s_2} ad esse parallele ma invece passanti per l’origine.

L’idea è quella di stabilire una relazione tra i rispettivi coefficienti angolari delle due rette passanti per l’origine, in modo da poter utilizzare il teorema di Pitagora. Ed a tal punto, sarà possibile estendere la relazione anche alle rette di partenza, ed in generale ad una qualunque coppia di rette aventi gli stessi coefficienti angolari delle rette di partenza stesse.

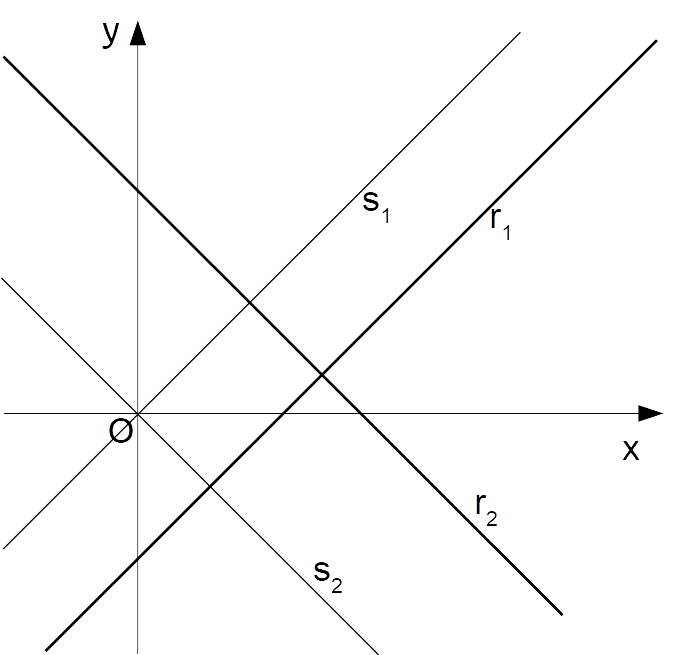
Osserviamo che le rette sono parallele a due a due. In altre parole, la retta {r_1} è parallela ad {s_1} e la retta {r_2} è parallela ad {s_2}. E poiché per ipotesi le rette {r_1} ed {r_2} sono tra loro perpendicolari, anche le rette {s_1} ed {s_2} lo sono.

La retta {s_1} ha equazione:

s_1:y=m_1x

mentre la retta {s_2} ha equazione:

s_2:y=m_2x

Si tratta effettivamente di equazioni relative a rette passanti per l’origine, in quanto della forma {y=mx} (ordinata all’origine {q} nulla).

Ora, dato il punto {P(1,0)}, la retta verticale passante per esso interseca le rette {s_1} ed {s_2} rispettivamente nei punti {A} e {B}.

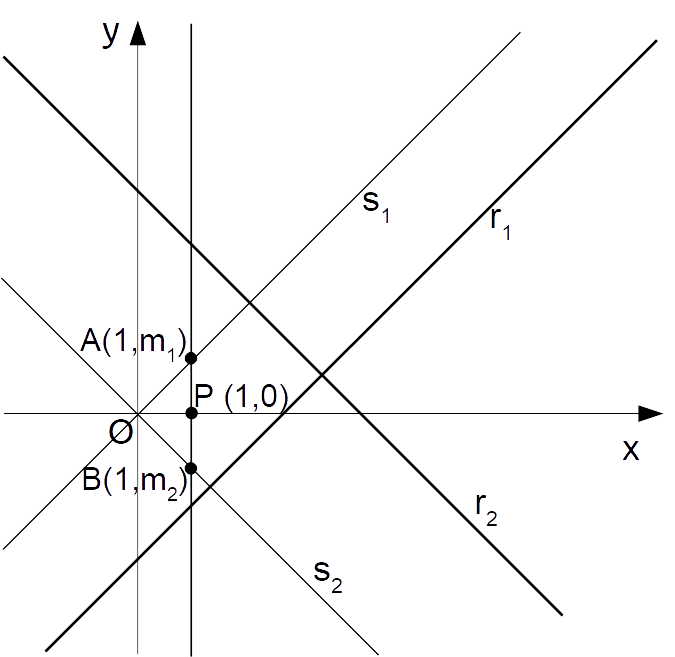
In particolare, il punto {A} della retta {s_1} ha coordinate:

y=m_1x \quad \text{con} \quad x=1 \quad \Rightarrow \quad y=m_1 \quad \Rightarrow A=(1,m_1)

mentre il punto {B} della retta {s_2} ha coordinate:

y=m_2x \quad \text{con} \quad x=1 \quad \Rightarrow \quad  y=m_2 \quad \Rightarrow B=(1,m_2)

A questo punto, osserviamo che in figura è possibile individuare il triangolo rettangolo {\stackrel{\triangle}{OAB}}, per il quale vale la relazione, in forza al teorema di Pitagora:

\overline{AB}^2=\overline{OA}^2+\overline{OB}^2 \qquad (*)

Ora, ricordando la nozione di distanza tra due punti nel piano cartesiano, tenendo conto delle coordinate dei punti {A} e {B} si ha:

\begin{align*} & \overline{AB}^2=(x_B-x_A)^2+(y_B-y_A)^2 =(1-1)^2+(m_2-m_1)^2=(m_2-m_1)^2 \\ \\ & \overline{OA}^2 = (x_A-x_O)^2+(y_A-y_O)^2=(1-0)^2+(m_1-0)^2=1+m_1^2 \\ \\ & \overline{OB}^2=(x_B-x_O)^2+(y_B-y_O)^2=(1-0)^2+(m_2-0)^2=1+m_2^2\end{align*}

Di conseguenza la * diviene:

(m_2-m_1)^2=1+m_1^2+1+m_2^2

ovvero:

\cancel{m_2^2}-2m_2m_1+\cancel{m_1^2}=2+\cancel{m_1^2}+\cancel{m_2^2}

da cui:

-2m_2m_1=2 \quad \Rightarrow \quad -m_2m_1=1 \quad \Rightarrow \quad m_2m_1=-1

e quindi in conclusione, supponendo {m_1 \neq 0}:

m_2=-\dfrac{1}{m_1} \qquad (**)

Ora, la relazione appena scritta non è valida solo per le rette {s_1} ed {s_2} ma anche per le rette {r_1} ed {r_2}. Infatti, quest’ultime sono rette parallele alle prime, ovvero hanno il loro stesso coefficiente angolare.

Così in generale per una qualunque coppia di rette del piano cartesiano non parallele agli assi cartesiani e tra loro perpendicolari dovrà valere la **. E sottolineiamo che tale relazione non ha senso per rette parallele agli assi cartesiani. Infatti, nella ** il coefficiente {m_1} non può essere nullo e di conseguenza la retta {s_1} (e quindi anche la {r_1}) non può essere orizzontale. Ed inoltre, per le rette verticali il coefficiente angolare non è definito, e di conseguenza la relazione ** non ha in questo caso significato.

Pertanto, possiamo affermare che se due rette sono perpendicolari tra loro e non sono parallele agli assi coordinati, allora per esse vale la relazione **.

Si può inoltre dimostrare anche il viceversa, ovvero che se per due rette vale la ** allora la due rette stesse sono perpendicolari tra loro.

Così riassumendo possiamo affermare quanto segue.

Due rette {r_1} ed {r_2} del piano cartesiano non parallele agli assi coordinati sono perpendicolari tra loro se e solo se il prodotto dei rispettivi coefficienti angolari {m_1} ed {m_2} è uguale a {-1}, o equivalentemente se fra i coefficienti angolari vale la relazione:{m_2 = -\dfrac{1}{m_1}}ovvero un coefficiente angolare è l’inverso del reciproco dell’altro.

Più semplicemente, data una retta con coefficiente angolare {m}, una qualunque retta avente coefficiente angolare {-\dfrac{1}{m}} sarà ad essa perpendicolare.

Così ad esempio, data la retta {r_1} di equazione:

r_1: y=m_1x+q_1

la retta {r_2} avente equazione:

r_2 :y=-\dfrac{1}{m_1}x+q

sarà perpendicolare ad {r_1}, per un qualunque fissato valore reale dell’ordinata all’origine {q}.

Esempi (rette perpendicolari con equazioni in forma esplicita)

Esempio 1

Stabilire se sono perpendicolari tra loro o meno le rette di equazioni {r_1: y=2x+3} e {r_2: y=-\dfrac{1}{2}x+7}.

Partiamo ad esempio dal coefficiente angolare della retta {r_1}. Si ha:

m_1 = 2

A questo punto, consideriamo l’inverso del reciproco di {m_1}:

-\dfrac{1}{m_1}=-\dfrac{1}{2}

Effettivamente ritroviamo il coefficiente angolare della retta {r_2}, in quanto dall’equazione della retta {r_2} si ricava immediatamente {m_2 = -\dfrac{1}{2}}.

Ma allora, dato che vale la relazione:

m_2 = -\dfrac{1}{m_1} 

possiamo in conclusione affermare che le due rette assegnate sono tra loro perpendicolari.

Come è infatti possibile vedere dalla seguente figura, le due rette dividono il piano cartesiano in quattro angoli tutti congruenti tra loro e di ampiezza uguale a 90 gradi.

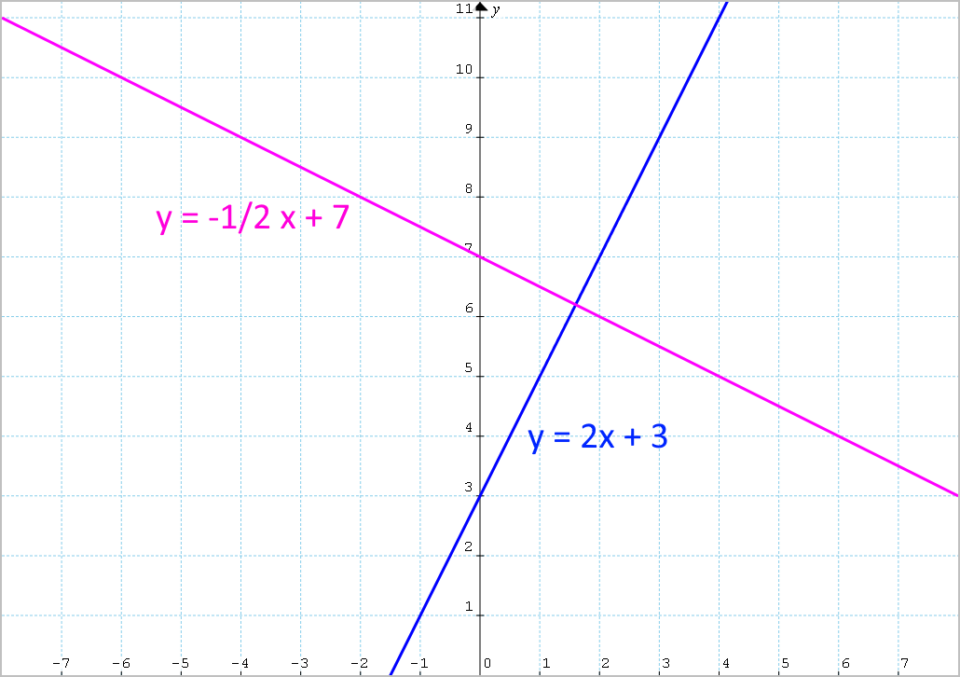
Osserviamo infine che avremmo potuto trarre le medesime conclusioni anche a partire dal coefficiente angolare {m_2} della retta {r_2}. Abbiamo infatti:

-\dfrac{1}{m_2}=-\dfrac{1}{-\frac{1}{2}}=\dfrac{1}{\frac{1}{2}}=2=m_1

da cui segue:

-\dfrac{1}{m_2}=m_1

ovvero, essendo {m_2 \neq 0}:

m_2m_1 = -1

che effettivamente è la condizione che caratterizza la perpendicolarità tra due rette aventi coefficiente angolare rispettivamente {m_1} ed {m_2}.

Esempio 2

Scrivere l’equazione di una retta tale da essere perpendicolare alla retta {r_1} di equazione {y=-3x+2}.

E’ sufficiente scrivere l’equazione di una retta avente coefficiente angolare uguale all’inverso del reciproco del coefficiente angolare della retta {r_1} (quest’ultimo dato da {m_1 = -3}), ed avente ordinata all’origine scelta a piacere. Ad esempio, detta {r_2} una tale retta, per il coefficiente angolare abbiamo:

m_2=-\dfrac{1}{m_1}=-\dfrac{1}{-3}=\dfrac{1}{3}

Per cui scegliendo ad esempio {q_2=4} possiamo scrivere l’equazione della retta {r_2} come:

r_2: y=\underbrace{\dfrac{1}{3}}_{m_2}x+\underbrace{4}_{q_2}

Sottolineiamo che un qualunque valore reale attribuito a {q_2} avrebbe comunque permesso di scrivere l’equazione di una retta perpendicolare ad {r_1}. Ad esempio la seguente retta:

r_3:y=\dfrac{1}{3}x-2

ove {q_2 = -2} è ancora perpendicolare alla retta {r_1}. E così via per ogni valore reale di volta in volta scelto per l’ordinata all’origine {q_2}.

Esempio 3

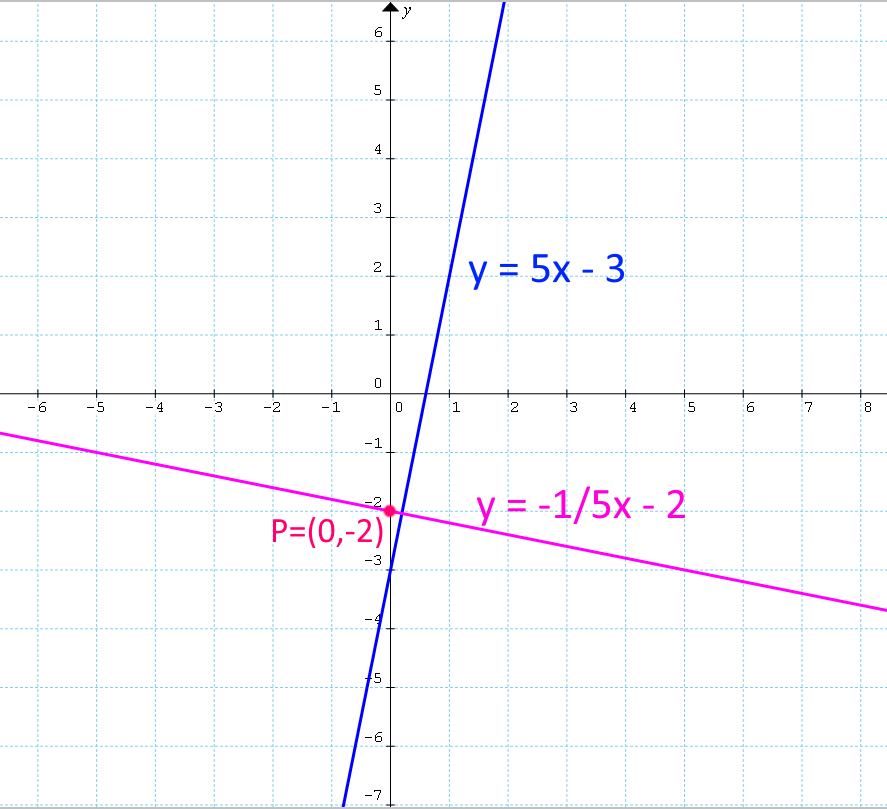
Determinare l’equazione della retta {r_2} perpendicolare alla retta {r_1: y=5x-3} e passante per il punto {P=(0,-2)}.

Ricordiamo anzitutto che una retta è univocamente determinata una volta note la sua pendenza e le coordinate di un punto appartenente alla retta stessa (vedi retta passante per un punto e con coefficiente angolare noto). Nel caso in esame, viene richiesto che la retta {r_2} sia perpendicolare ad una retta con coefficiente angolare noto. Di conseguenza, il coefficiente angolare della retta {r_2} è immediatamente calcolabile come l’inverso del reciproco del coefficiente angolare della retta {r_1}.

Così, essendo anche note le coordinate di un punto appartenente alla retta {r_2}, è possibile scrivere l’equazione di tale retta utilizzando l’equazione di una retta del piano cartesiano passante per un punto dato e di pendenza nota:

y-y_0=m(x-x_0)

ove {x_0, y_0} sono le coordinate del punto dato.

Di conseguenza, venendo al nostro caso, il primo passo da fare è calcolare il coefficiente angolare {m_2} della retta {r_2} a partire dal coefficiente angolare {m_1} della retta {r_1}:

m_2 =-\dfrac{1}{m_1}=-\dfrac{1}{5}

Poiché la retta {r_2} deve anche passare per il punto {P=(x_0, y_0)=(0,-2)} si ha:

y-y_0=m_2(x-x_0) \quad \Rightarrow \quad y-(-2)=-\dfrac{1}{5}(x-0) 

ovvero:

y=-\dfrac{1}{5}x-2

e questa è l’equazione della retta {r_2} tale da essere perpendicolare alla retta {r_1} e tale inoltre da passare per il punto {P=(0,-2)}.

Condizione di perpendicolarità tra rette con equazioni date in forma implicita

Vogliamo ora mostrare come esprimere la condizione di perpendicolarità tra rette del piano nel caso in cui le rispettive equazioni siano date in forma implicita. In particolare, il nostro obiettivo sarà quello di verificare la perpendicolarità tra rette a partire dai coefficienti dei termini in {x} e {y} che compaiono nelle equazioni in forma implicita delle rette stesse. Ciò è del tutto simile all’approccio utilizzato per stabilire una condizione di parallelismo tra rette del piano con equazioni date in forma implicita.

Cominciamo ricordando che l’equazione di una retta in forma implicita si scrive come:

ax+by+c=0, \qquad a,b,c \in \R

ove {a} e {b} non sono mai contemporaneamente nulli.

Ora, come già mostrato nella lezione del link abbiamo:

m=-\dfrac{a}{b}

Così date due rette {r_1} ed {r_2} non parallele agli assi coordinati con equazioni espresse in forma implicita:

r_1: a_1x+b_1y+c_1=0, \qquad r_2:a_2x+b_2y+c_2=0

i rispettivi coefficienti angolari si esprimono come:

m_1=-\dfrac{a_1}{b_1}; \qquad m_2=-\dfrac{a_2}{b_2}

e la relazione di perpendicolarità tra due rette sin qui discussa:

m_2 = -\dfrac{1}{m_1}

utilizzando i coefficienti {a_1, b_1, a_2, b_2} diviene:

-\dfrac{a_2}{b_2}=-\dfrac{1}{-\frac{a_1}{b_1}} \quad \Rightarrow \quad -\dfrac{a_2}{b_2}=\dfrac{b_1}{a_1}

Trasportando tutti i termini al primo membro e riducendoli a denominatore comune otteniamo:

-\dfrac{a_2}{b_2}-\dfrac{b_1}{a_1}=0 \quad \Rightarrow \quad \dfrac{-a_2 \cdot a_1 -b_1 \cdot b_2 }{b_2 \cdot a_1} = 0

ovvero, poiché necessariamente {b_2 \neq 0} e {a_1 \neq 0} (le rette non sono parallele agli assi coordinati):

-a_2 \cdot a_1 -b_1 \cdot b_2 = 0

e quindi in conclusione:

\boxed{a_1 \cdot a_2 +b_1 \cdot b_2 = 0}

Osserviamo che ponendo ad esempio {a_1=b_2} e {a_2=-b_1} la precedente condizione risulta verificata:

b_2 \cdot (-b_1)+b_1 \cdot b_2 = 0 \quad \Rightarrow \quad 0=0

In alternativa si perviene allo stesso risultato ponendo {a_1 =-b_2} e {a_2=b_1}:

-b_2 \cdot b_1+b_1 \cdot b_2 = 0   \quad \Rightarrow \quad 0=0

Da ciò deriviamo la seguente regola generale.

Data l’equazione di una retta del piano cartesiano non parallela agli assi coordinati espressa in forma implicita, l’equazione che si ottiene scambiando tra loro i coefficienti dei termini in {x} e {y} e cambiando il segno di uno solo di essi è quella relativa ad una retta del piano ad essa perpendicolare. Inoltre, il termine noto potrà assumere un qualunque valore reale, in corrispondenza del quale otterremo sempre una retta perpendicolare a quella data in partenza.
Così, in simboli, data la retta {r_1} di equazione:{r_1: a_1x+b_1y+c_1 = 0 }la retta {r_2} di equazione: {r_2 : b_1 x -a_1 y+k = 0}rappresenta una retta perpendicolare a {r_1}, per un qualunque fissato valore reale di {k}.

Esempi (condizione di rette perpendicolari a partire dalle equazioni in forma implicita)

Esempio 1

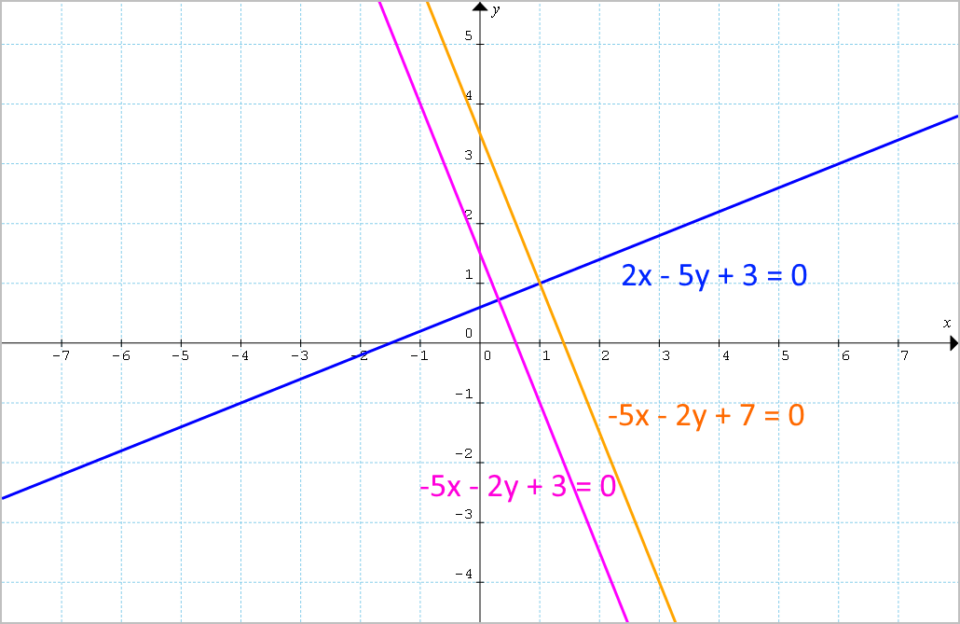
Scrivere l’equazione di una retta perpendicolare alla retta {r_1} di equazione {2x-5y+3=0}.

Scambiamo tra loro i coefficienti dei termini in {x} e {y}, cambiando inoltre il segno soltanto ad uno dei due coefficienti:

r_2 :  -5x-2y+3=0

Osserviamo che il coefficiente del termine in {x} dell’equazione della retta {r_2} è il coefficiente del termine in {y} dell’equazione della retta {r_1}, mentre il coefficiente del termine in {y} dell’equazione della retta {r_2} è il coefficiente del termine in {x} dell’equazione della retta {r_1} cambiato di segno.

Così, per la regola su esposta {r_2} è una retta perpendicolare ad {r_1}. E attribuendo al termine noto dell’equazione di {r_2} un qualunque valore reale otteniamo comunque una retta perpendicolare ad {r_1}. Così ad esempio la retta:

r_3:-5x-2y+7=0

è ancora una retta del piano cartesiano tale da essere perpendicolare alla retta {r_1}.

Esempio 2

Stabilire se le rette {r_1: -3x+2y-5=0} e {r_2 : 2x-3y+4=0} sono tra loro perpendicolari.

Osserviamo che i coefficienti dei termini in {x} e in {y} passando da un’equazione all’altra risultano effettivamente scambiati. Tuttavia, entrambi i coefficienti conservano il segno. Di conseguenza, le rette non sono tra loro perpendicolari.

Nell’esempio a seguire presentiamo un metodo che consente di stabilire se due rette con equazioni date in forma implicita sono perpendicolari tra loro riconducendo entrambe le rispettive equazioni alla forma esplicita. Una volta fatto ciò, basterà utilizzare la condizione di perpendicolarità tra rette basata sui coefficienti angolari, così come abbiamo visto nella prima parte della lezione.

Esempio 3 (metodo alternativo)

Stabilire se le rette {r_1: 2x+5y-6=0} e {r_2:-5x+2y+4=0} sono tra loro perpendicolari.

Riconduciamo entrambe le equazioni alla forma esplicita:

r_1:y=-\dfrac{2}{5}x+\dfrac{6}{5}, \qquad r_2:y=\dfrac{5}{2}x-2

Il coefficiente angolare della retta {r_1} è uguale a {m_1 = -\dfrac{2}{5}}, mentre il coefficiente angolare della retta {r_2} è uguale a {m_2 = \dfrac{5}{2}}. Osserviamo che ciascun coefficiente angolare è l’inverso del reciproco dell’altro. Di conseguenza, le due rette date sono tra loro perpendicolari.

A conclusione della lezione, l’esempio a seguire mostra l’importanza del prestare particolare attenzione ai segni dei coefficienti dei termini in {x} e {y} presenti nelle equazioni in esame.

Esempio 4

Stabilire se le rette di equazioni {r_1:-2x-5y+3=0} e {r_2:5x+2y+4=0} sono tra loro perpendicolari.

Osserviamo che passando da un’equazione all’altra i valori assoluti dei coefficienti in {x} ed {y} risultano tra loro scambiati. Tuttavia, nel passare da un’equazione all’altra si rileva che entrambi i segni dei coefficienti risultano cambiati. Di conseguenza le due rette non sono tra loro perpendicolari, poiché per la perpendicolarità avremmo dovuto avere un cambio di segno relativo soltanto ad uno dei due coefficienti.

Conclusioni

Per quanto riguarda questa lezione sulle condizioni caratterizzanti le rette perpendicolari è tutto. Nella prossima lezione ci occuperemo del problema relativo all’intersezione di due rette, per il quale ci sarà di fondamentale aiuto quanto visto a suo tempo relativamente ai sistemi lineari. Buon proseguimento ed un saluto a tutti voi! 🙂