Intersezione tra due rette

 - 

Coordinate cartesiane e retta nel piano

In questa lezione ci occuperemo del problema del calcolo delle coordinate dell’eventuale punto di intersezione tra due rette. E più in generale, studieremo i vari casi che possiamo incontrare nell’effettuare l’intersezione tra due rette del piano cartesiano.

In una precedente lezione abbiamo visto la condizione di appartenenza di un punto ad una retta del piano. Come vedremo tra un istante, due rette hanno un certo punto di intersezione se le coordinate cartesiane di tale punto soddisfano entrambe le condizioni di appartenenza a ciascuna retta. Così, se un dato punto {P=(x_0, y_0)} risulta appartenere ad entrambe le rette {r_1} ed {r_2}, allora questo sarà punto di intersezione delle due rette.

Tuttavia, in generale non è detto che due rette del piano cartesiano abbiano sempre un punto di intersezione. Infatti, se consideriamo ad esempio due rette del piano tra loro parallele non coincidenti, queste non avranno alcun punto di intersezione. E in più, se tale punto invece esiste, non è detto che sia unico. Infatti, se due rette sono parallele e coincidenti, queste hanno infiniti punti di intersezione.

Così nell’effettuare l’intersezione tra due rette del piano possiamo distinguere tre casi: rette non parallele tra loro o rette incidenti (esiste un unico punto di intersezione), rette parallele e non coincidenti (nessun punto di intersezione), ed infine rette parallele e coincidenti (infiniti punti di intersezione).

Ora, come vedremo tra breve il calcolo delle coordinate del punto di intersezione tra due rette si effettua risolvendo un certo sistema lineare, ed in particolare un sistema nel quale figurano le equazioni relative alle rette in esame.

Come sappiamo, un sistema lineare può in generale essere determinato, indeterminato o impossibile. E, nel caso dell’intersezione tra due rette del piano, se il corrispondente sistema è determinato, allora esiste un unico punto di intersezione tra le due rette. Se invece il sistema è indeterminato, allora esistono infiniti punti di intersezione tra le due rette (rette parallele e coincidenti). Infine, se il sistema è impossibile, allora le due rette non presentano alcun punto di intersezione e sono parallele e distinte (parallele non coincidenti).

Dopo questa breve introduzione, vediamo di comprendere gradualmente come calcolare le coordinate dell’eventuale punto di intersezione tra due rette del piano cartesiano.

Intersezione tra due rette del piano cartesiano

Date due rette {r_1} ed {r_2} del piano cartesiano, queste possono essere:

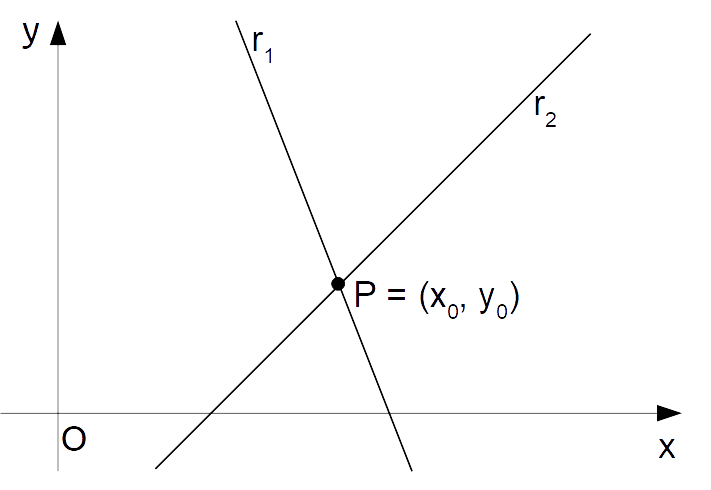
• incidenti, se hanno un unico punto in comune (punto di intersezione). In tal caso le rette risultano non parallele tra loro;

• coincidenti (parallele coincidenti), se hanno infiniti punti in comune. In tal caso le due rette condividono gli stessi punti ed hanno di conseguenza infiniti punti di intersezione (ovvero hanno tutti i punti in comune);

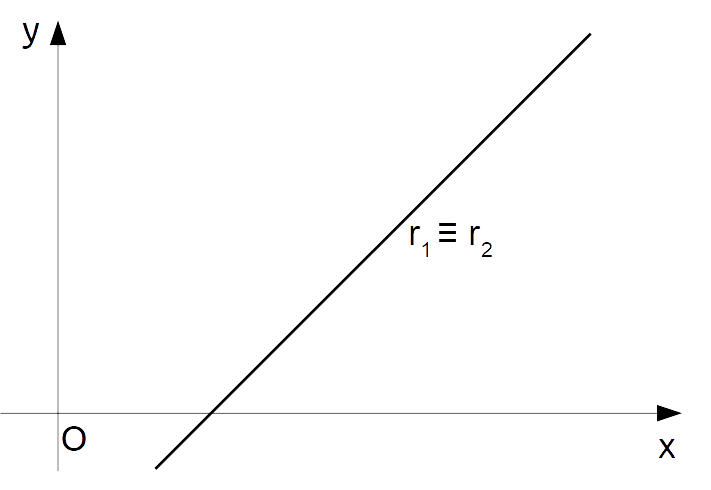
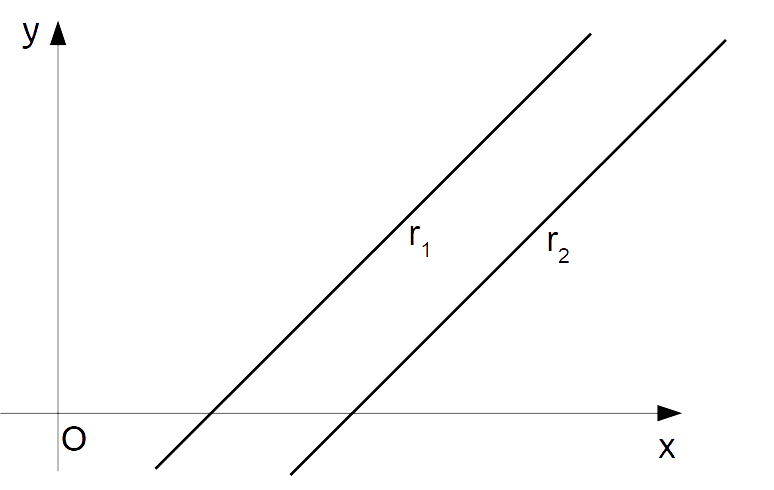
• parallele non coincidenti, se non hanno alcun punto di intersezione. In quest’ultimo caso, le due rette non hanno nessun punto in comune.

Nota: con linguaggio meno formale, quando si parla di “rette parallele” ci si riferisce solitamente a rette parallele non coincidenti, escludendo implicitamente il caso delle rette coincidenti. Raccomandiamo comunque l’utilizzo delle definizioni di “rette parallele non coincidenti” e di “rette coincidenti”, onde evitare ambiguità.

Importante. Attenzione a non confondere tra loro i termini “incidenti” e “coincidenti”. Sottolineiamo ancora come due rette “incidenti” nel piano hanno necessariamente uno ed un solo punto di intersezione. Invece, due rette “coincidenti” hanno tutti i punti in comune tra loro.
Così, nel caso di rette tra loro parallele ma prive di punti in comune utilizzeremo il termine “rette parallele non coincidenti”.
Infine, attenzione a non utilizzare per errore la definizione “rette parallele non incidenti”. Quest’ultima infatti non ha significato (o meglio è ridondante) poiché è ovvio che se due rette sono parallele tra loro queste non possono essere incidenti (due rette parallele non possono certo avere un unico punto in comune).

Intersezione tra rette del piano e sistemi lineari

Consideriamo due rette del piano cartesiano aventi equazioni (ad esempio in forma implicita):

r_1: a_1x+b_1y+c_1=0, \qquad r_2:a_2x+b_2y+c_2=0

ove i coefficienti dei termini in {x} e {y} ed i termini noti sono tutti numeri reali. Inoltre, in entrambe le equazioni i coefficienti dei termini in {x} e {y} non sono mai entrambi nulli.

L’eventuale punto di intersezione {P=(x_0, y_0)} tra le due rette si determina risolvendo ad esempio per riduzione il sistema lineare:

\begin{cases} a_1x+b_1y+c_1=0\\ \\a_2x+b_2y+c_2=0\end{cases}

ove compaiono le equazioni delle rette {r_1} ed {r_2}.

Le coordinate dell’eventuale punto di intersezione tra due rette {r_1} ed {r_2} del piano cartesiano si ottengono risolvendo il sistema lineare nel quale compaiono le equazioni di ciascuna retta, se questo è determinato.

In particolare, nel caso in cui il sistema risulta determinato, allora esistono due valori {x_0} ed {y_0} tali da soddisfare entrambe le equazioni a sistema. Così, la coppia di valori {(x_0, y_0)} è in questo caso soluzione del sistema in esame. E di conseguenza, il punto {P=(x_0, y_0)} rappresenta il punto di intersezione tra le due rette del piano.

Se invece il sistema risulta indeterminato, questo ammette infinite soluzioni. E di conseguenza, esistono infinite coppie del tipo {(x,y)} tali da soddisfare il sistema. Ma ciò significa che esistono infiniti punti tali da appartenere ad entrambe le rette {r_1} ed {r_2}. E questo, per concludere, richiede necessariamente che le due rette siano parallele e coincidenti (le due rette hanno tutti i punti in comune).

Infine, nel caso di sistema impossibile, non esiste alcuna coppia {(x_0, y_0)} tale da essere soluzione per il sistema. Così, non esiste alcun punto {P=(x_0, y_0)} in comune tra le due rette. Ci ritroviamo quindi nel caso di due rette parallele e non coincidenti (o parallele e distinte).

Importante. Come sappiamo dalla teoria sui sistemi lineari, un sistema lineare in forma normale è in realtà della forma:{\begin{cases} a_1x+b_1y=k_1 \\ \\ a_2x+b_2y=k_2\end{cases}}ovvero i termini noti si trovano al secondo membro. Tuttavia, se per risolvere il sistema utilizziamo il metodo di riduzione, allora ha comunque senso mettere a sistema le equazioni delle rette nella forma implicita. Il metodo di riduzione può infatti essere utilizzato senza alcun problema anche se in tutte le equazioni a sistema i secondi membri sono uguali a zero.
Nel caso in cui invece, attenzione, si desideri risolvere il sistema utilizzando la regola di Cramer, è allora obbligatorio ricondurre il sistema alla forma normale. In altre parole, volendo utilizzare la regola di Cramer, dobbiamo scrivere le equazioni delle rette in una forma tale che al secondo membro ci ritroviamo i soli termini noti.

Ora, nel caso in cui le equazioni delle rette siano date in forma esplicita:

r_1:y=m_1x+q_1, \qquad r_2:y=m_2x+q_2

il sistema da risolvere per determinare le coordinate dell’eventuale punto di intersezione tra le due rette è:

\begin{cases} y=m_1x+q_1 \\ \\ y=m_2x+q_2\end{cases}

In questo caso, poiché in entrambe le equazioni risulta esplicitata la variabile {y}, per risolvere il sistema può essere conveniente utilizzare il metodo del confronto. In particolare, basterà sostituire una delle due equazioni a sistema con l’equazione che si ottiene uguagliando tra loro i secondi membri delle equazioni di partenza. Ad esempio:

\begin{cases} m_1x+q_1=m_2x+q_2 \\ \\ y=m_2x+q_2\end{cases}

In questo modo, se le due rette sono incidenti, sarà immediato ricavare il valore numerico dell’incognita {x} dalla prima equazione. E a tal punto, basterà sostituire il valore così ottenuto nel secondo membro della seconda equazione, ottenendo in conclusione il valore numerico dell’incognita {y}. Così, le coordinate {x_0} e {y_0} del punto di intersezione {P=(x_0, y_0)} delle due rette saranno note.

Vediamo subito degli esempi su come calcolare le coordinate dell’eventuale punto di intersezione tra due rette del piano cartesiano.

Esempio 1

Stabilire se le rette {r_1:2x+5y-7=0} e {r_2: 3x-4y+5=0} sono incidenti, parallele e distinte oppure coincidenti.

Il nostro obiettivo sarà vedere se il sistema dato dalle equazioni delle due rette:

\begin{cases} 2x+5y-7=0 \\ \\ 3x-4y+5=0 \end{cases}

è determinato, impossibile oppure indeterminato.

Le equazioni delle due rette sono date in forma implicita e non è dunque conveniente utilizzare il metodo del confronto. Piuttosto, procediamo per riduzione:

\begin{align*} & \begin{cases} 6x+15y-21=0 \\ \\ -6x+8y-10=0\end{cases} \quad \Rightarrow \quad \begin{cases} 23y-31=0 \\ \\ -6x+8y-10=0\end{cases}  \quad \Rightarrow \quad \\ \\ & \Rightarrow\begin{cases} y=\dfrac{31}{23} \\ \\ x=\dfrac{4}{3}\cdot \dfrac{31}{23}-\dfrac{5}{3}=\dfrac{124}{69}-\dfrac{5}{3}=\dfrac{124-115}{69}=\dfrac{9}{69}=\dfrac{3}{23}\end{cases} \end{align*} 

e quindi:

\begin{cases} y=\dfrac{31}{23} \\ \\ x =\dfrac{3}{23} \end{cases}

Possiamo allora concludere dicendo che il sistema è determinato e di conseguenza il punto {P=\left( \dfrac{3}{23}, \dfrac{31}{23}\right)} è il punto di intersezione tra le due rette date.

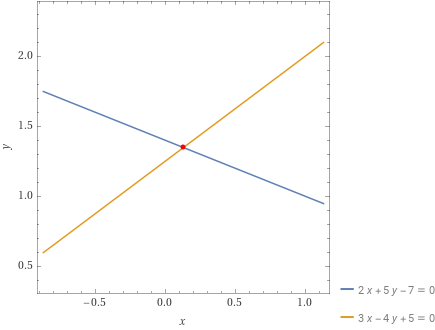
Osservazione. E’ immediato verificare se due rette del piano sono incidenti confrontando i rispettivi coefficienti angolari. Infatti, se due rette del piano hanno differenti coefficienti angolari, queste sono incidenti.
Nel nostro caso, dalla prima equazione otteniamo {m_1=-\dfrac{a_1}{b_1}=-\dfrac{2}{5}}, mentre dalla seconda abbiamo {m_2=-\dfrac{a_2}{b_2}=\dfrac{3}{4}}. I due coefficienti angolari sono diversi tra loro e di conseguenza le due rette del piano, avendo differente pendenza, risultano necessariamente incidenti (ovvero presentano un unico punto in comune).

Esempio 2

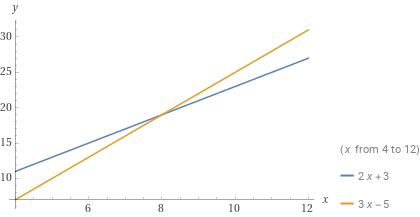
Determinare l’eventuale punto di intersezione tra le due rette {r_1: y=2x+3} e {r_2: y=3x-5}.

Cominciamo scrivendo un sistema lineare comprendente le equazioni delle rette date:

\begin{cases} y=2x+3 \\ \\ y=3x-5\end{cases}

Le equazioni sono entrambe in forma esplicita, e quindi può essere conveniente risolvere il sistema utilizzando il metodo del confronto:

\begin{cases} 2x+3=3x-5  \\ \\ y=3x-5\end{cases} \quad \Rightarrow \quad \begin{cases} 2x-3x=-5-3 \quad \rightarrow \quad x=8 \\ \\ y=3 \cdot 8 - 5 = 19\end{cases}

Il sistema è determinato e quindi in conclusione le due rette hanno come intersezione il punto {P=(8, 19)}.

Esempio 3

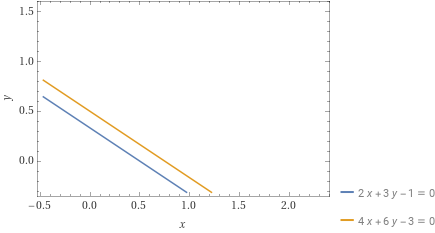
Determinare le coordinate dell’eventuale punto di intersezione tra le rette {r_1:2x+3y-1=0} e {r_2 : 4x+6y-3=0}.

Possiamo accorgerci immediatamente che le due rette sono parallele non coincidenti. Infatti, queste hanno i coefficienti dei termini in {x} e {y} proporzionali tra loro ed inoltre hanno differente ordinata all’origine {q=-\dfrac{c}{b}}. Per meglio convincersi, basta un breve ripasso sulla condizione di parallelismo tra rette del piano.

Se comunque non riusciamo ad accorgerci di questo, nessun problema. Possiamo ugualmente provare a risolvere l’opportuno sistema e vedere cosa succede. Nel nostro caso abbiamo:

\begin{cases} 2x+3y-1=0 \\ \\  4x+6y-3=0\end{cases}

Risolvendo per riduzione otteniamo:

\begin{cases} -4x-6y+2=0 \\ \\ 4x+6y-3=0\end{cases} \quad \Rightarrow \quad \begin{cases} -1 = 0 \\ \\ 4x+6y-3=0\end{cases}

Ora, poiché nella prima equazione a sistema ci ritroviamo con l’uguaglianza numerica {-1=0}, che è falsa, il sistema è impossibile. Di conseguenza, le due rette non hanno alcun punto in comune e pertanto le due rette sono parallele non coincidenti.

Esempio 4

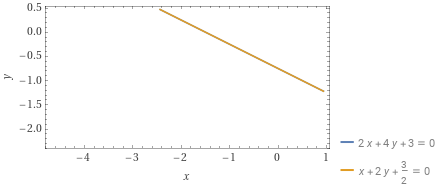
Stabilire se sono incidenti o meno le rette {r_1:2x+4y+3=0} e {r_2:x+2y+\dfrac{3}{2}=0}.

E’ immediato osservare che le due rette sono coincidenti. Infatti, grazie ai principi di equivalenza è possibile ricondursi da un’equazione all’altra. In particolare, l’equazione della retta {r_2} si ottiene a partire dall’equazione della retta {r_1} dividendo tutti i termini per {2}.

Scrivendo comunque il sistema e provando a risolvere per riduzione abbiamo:

\begin{cases}2x+4y+3=0 \\ \\ x+2y+\dfrac{3}{2}=0  \end{cases}  \quad \Rightarrow \quad \begin{cases} 2x+4y+3=0 \\ \\ 2x+4y+3=0\end{cases} \quad \Rightarrow \quad \begin{cases} 0=0 \\ \\ 2x+4y+3=0\end{cases}

Poiché ci ritroviamo con un’identità (l’uguaglianza numerica 0=0), il sistema è indeterminato e di conseguenza le due rette sono coincidenti. Ritroviamo così conferma di quanto già intuito grazie ai principi di equivalenza delle equazioni.

Conclusioni

Per quanto riguarda il problema dell’intersezione tra rette del piano cartesiano è tutto. Nella prossima lezione ci occuperemo della distanza tra un punto e una retta nel piano, per poi passare alla successiva lezione dedicata ai fasci di rette. Buon proseguimento con Sìmatematica!